Deck 7: Project Schedule Planning and Networks
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/26
Play
Full screen (f)
Deck 7: Project Schedule Planning and Networks
1
If an activity has two immediate predecessors and their early finish times are 15 and 19, respectively, then the early start time of that activity must be:
A) 15
B) 19
C) cannot be determined from this information
A) 15
B) 19
C) cannot be determined from this information
19
2
If an activity has two immediate successors and their late start times are 26 and 33, respectively, then the late finish time of that activity must be:
A) 26
B) 33
C) cannot be determined from this information
A) 26
B) 33
C) cannot be determined from this information
26
3
Which one of the following statements is true:
A) in an AOA diagram, each activity is represented as a line.
B) in an AON diagram, each activity is represented as a square.
C) in an AOA diagram, nodes represent events.
D) both a and b
E) a, b, and c
A) in an AOA diagram, each activity is represented as a line.
B) in an AON diagram, each activity is represented as a square.
C) in an AOA diagram, nodes represent events.
D) both a and b
E) a, b, and c
a, b, and c
4
In a network, the critical path is that sequence of activities that requires:
A) the longest time to complete
B) the shortest time to complete
C) both a and b
A) the longest time to complete
B) the shortest time to complete
C) both a and b

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
5
In a network, the critical path indicates:
A) the shortest possible time in which the project can be done
B) the longest possible duration of the project
C) neither (a) nor (b)
D) both (a) and (b)
A) the shortest possible time in which the project can be done
B) the longest possible duration of the project
C) neither (a) nor (b)
D) both (a) and (b)

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
6
The early expected start time, ES, of an activity depends on the completion:
A) of the latest EF of all of the immediate predecessor activities
B) of the earliest EF of all of the immediate predecessor activities
C) neither a nor b
A) of the latest EF of all of the immediate predecessor activities
B) of the earliest EF of all of the immediate predecessor activities
C) neither a nor b

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
7
The latest allowable finish time that an event can occur, LF, depends on:
A) the earliest possible start time of all of its immediate predecessors
B) the latest allowable start times of all of its immediate predecessors
C) neither a nor b
A) the earliest possible start time of all of its immediate predecessors
B) the latest allowable start times of all of its immediate predecessors
C) neither a nor b

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
8
Doing a project fast has the following advantages:
A) achieving benefits sooner.
B) reduced risk of stakeholders' needs changing.
C) guarantees success since all projects have a predetermined due date.
D) all of the above.
E) (a) and (b) above.
A) achieving benefits sooner.
B) reduced risk of stakeholders' needs changing.
C) guarantees success since all projects have a predetermined due date.
D) all of the above.
E) (a) and (b) above.

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
9
The advantages of scheduling include all of the following EXCEPT:
A) is necessary in order to determine the cash flow.
B) is necessary in order to determine the workload on individuals
C) provides absolute certainty about the end date.
D) is necessary in order to utilize resources efficiently.
A) is necessary in order to determine the cash flow.
B) is necessary in order to determine the workload on individuals
C) provides absolute certainty about the end date.
D) is necessary in order to utilize resources efficiently.

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
10
The following technique requires the use of "dummy" activities:
A) the Gantt chart.
B) the AON network method.
C) the AOA network method.
D) the critical chain method.
E) all logic diagramming methods.
A) the Gantt chart.
B) the AON network method.
C) the AOA network method.
D) the critical chain method.
E) all logic diagramming methods.

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
11
If Activity A has to be performed before Activity B can start, then:
A) A is a predecessor to B.
B) B is a predecessor to A.
C) there is a discretionary dependency or external dependency between A and B.
D) the relationship between A and B can only be indicated on an AON network.
A) A is a predecessor to B.
B) B is a predecessor to A.
C) there is a discretionary dependency or external dependency between A and B.
D) the relationship between A and B can only be indicated on an AON network.

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
12
The critical path:
A) is shortest path through a project network.
B) does not change during project execution.
C) always has zero slack.
D) has the smallest slack in the project.
E) all of the above.
A) is shortest path through a project network.
B) does not change during project execution.
C) always has zero slack.
D) has the smallest slack in the project.
E) all of the above.

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
13
In a start-to-start relationship, a 2-day lag implies that:
A) the successor should not start until two days after the predecessor has been completed.
B) the successor should not start until two days after the predecessor has started.
C) the successor can start two days before the predecessor has started.
D) the two activities can start on the same date.
A) the successor should not start until two days after the predecessor has been completed.
B) the successor should not start until two days after the predecessor has started.
C) the successor can start two days before the predecessor has started.
D) the two activities can start on the same date.

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
14
The criticism of network techniques that some project work cannot be known beforehand can be somewhat overcome by:
A) drawing a Gantt chart.
B) using the AON method.
C) never planning project activities in detail.
D) using a suitable computer system.
E) breaking the project down into phases and planning only the imminent phase in detail.
A) drawing a Gantt chart.
B) using the AON method.
C) never planning project activities in detail.
D) using a suitable computer system.
E) breaking the project down into phases and planning only the imminent phase in detail.

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
15
Resource leveling:
A) makes use of float (slack) to move activities to to time slots other than the "as early as possible" dates.
B) makes the workload on resources more evenly distributed.
C) can potentially turn non-critical activities into critical ones.
D) all of the above.
E) (a) and (b) above.
A) makes use of float (slack) to move activities to to time slots other than the "as early as possible" dates.
B) makes the workload on resources more evenly distributed.
C) can potentially turn non-critical activities into critical ones.
D) all of the above.
E) (a) and (b) above.

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
16
The forward and backward pass:
A) determine the early and late start dates of activities, respectively.
B) determine the float (slack) of activities.
C) determine the critical path.
D) all of the above.
E) (a) and (c) above
A) determine the early and late start dates of activities, respectively.
B) determine the float (slack) of activities.
C) determine the critical path.
D) all of the above.
E) (a) and (c) above

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
17
In the PDM method (circle all that are true):
A) activities cannot be started before immediate predecessors are completed
B) activities can be repeated
C) activities can be started when immediate predecessors are only partially completed
D) there is more flexibility in scheduling than in the usual finish-to-start method
A) activities cannot be started before immediate predecessors are completed
B) activities can be repeated
C) activities can be started when immediate predecessors are only partially completed
D) there is more flexibility in scheduling than in the usual finish-to-start method

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
18
Statement: The term "dummy activity" is a misnomer since each dummy represents work, takes time, and requires use of resources.

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
19
Statement: Redundant activities are activities that are repetitive of others and can be deleted from the project.

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
20
Statement: There can only be one critical path in a network.

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
21
Statement: If an activity has multiple predecessors, its late start is determined by the latest finish of its predecessors.

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
22
Statement: The total slack of each of the activities on a subpath will be the same as the total slack of the other activities on the subpath.

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
23
Statement: The free slack of each of the activities on a subpath will be the same as the free slack of the other activities on the subpath.

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
24
Use the table and network below to answer parts (a) through (d).
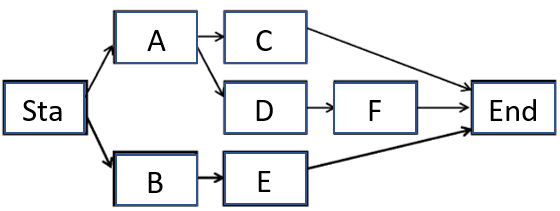 (a) On the network above, show ES, EF, LS, and LF for every event.
(a) On the network above, show ES, EF, LS, and LF for every event.
(b) Below, construct a Gantt chart for the network using only ES's and EF's.
 (C)Using costs from the table and the Gantt chart in (b), show weekly costs for the project.
(C)Using costs from the table and the Gantt chart in (b), show weekly costs for the project.
 (d) Below, using the chart in (c) as a guide, construct a chart showing estimated cumulative project expenditures.
(d) Below, using the chart in (c) as a guide, construct a chart showing estimated cumulative project expenditures.
 (a) On the network above, show ES, EF, LS, and LF for every event.
(a) On the network above, show ES, EF, LS, and LF for every event.(b) Below, construct a Gantt chart for the network using only ES's and EF's.
 (C)Using costs from the table and the Gantt chart in (b), show weekly costs for the project.
(C)Using costs from the table and the Gantt chart in (b), show weekly costs for the project. (d) Below, using the chart in (c) as a guide, construct a chart showing estimated cumulative project expenditures.
(d) Below, using the chart in (c) as a guide, construct a chart showing estimated cumulative project expenditures. 

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
25
Use the following Gantt chart and table to answer questions (a) and (b).
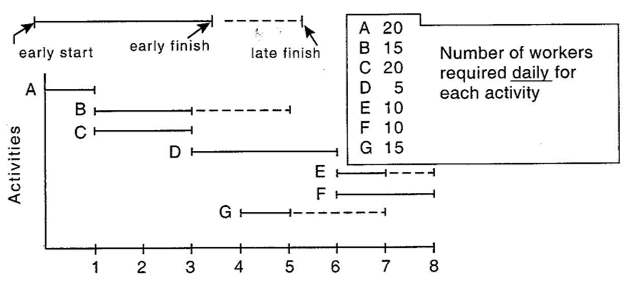 (a) On this diagram, show the total daily workers required (loading) assuming early start times for all activities. Show what portion of the total labor loading each day comes from each activity.
(a) On this diagram, show the total daily workers required (loading) assuming early start times for all activities. Show what portion of the total labor loading each day comes from each activity.
 (b) On this diagram, balance the loading of workers by shifting activities so that no more than 20 workers per day are needed. Assume that the project must be completed in eight days.
(b) On this diagram, balance the loading of workers by shifting activities so that no more than 20 workers per day are needed. Assume that the project must be completed in eight days.
 (a) On this diagram, show the total daily workers required (loading) assuming early start times for all activities. Show what portion of the total labor loading each day comes from each activity.
(a) On this diagram, show the total daily workers required (loading) assuming early start times for all activities. Show what portion of the total labor loading each day comes from each activity. (b) On this diagram, balance the loading of workers by shifting activities so that no more than 20 workers per day are needed. Assume that the project must be completed in eight days.
(b) On this diagram, balance the loading of workers by shifting activities so that no more than 20 workers per day are needed. Assume that the project must be completed in eight days.

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
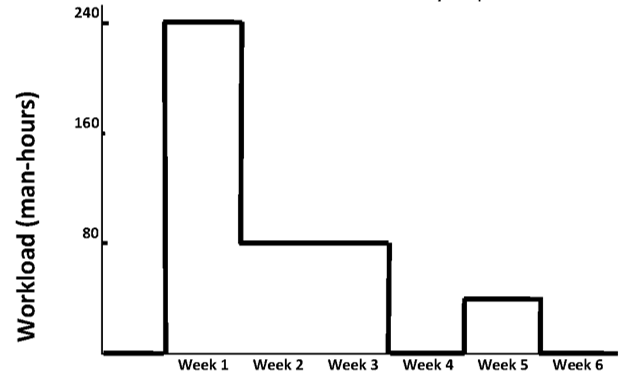
26
Level the resources for the activities below:
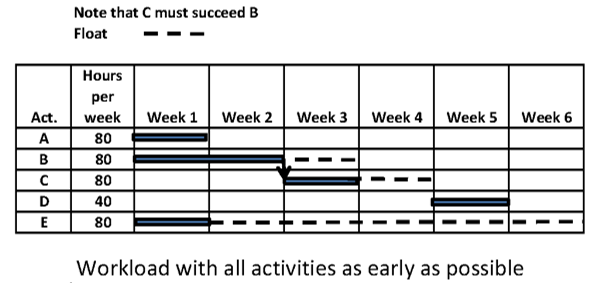



Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck


