Deck 5: Finitely-Repeated, Static Games

Question 1

-Consider the two-stage, static game depicted in Figure 5.1 involving two companies that enter into an agreement to maximize total profits. The payoffs in this game are in millions of dollars. The optimal strategy for both firms is to:

A) Play B in stage 1 and stage 2.
B) Play B in stage 1 and play A in stage 2.
C) Play C in stage 1 and stage 2.
D) Play B in stage 1 and play C in stage 2.
E) Play C in stage 1 and play B in stage 2.

Answer 1

Play B in stage 1 and stage 2.

Question 2

-Consider the two-stage game depicted in Figure 5.2 involving two companies that enter into an agreement to maximize total profits. The payoffs in this game are in millions of dollars. The optimal strategy for both firms is to:

A) Play X in stage 1 and play Y in stage 2.
B) Play Y in stage 1 and play Z in stage 2.
C) Play X in stage 1 and play Z in stage 2.
D) Play X in stage 1 and stage 2.
E) Play Y in stage 1 and stage 2.

Answer 2

Play Y in stage 1 and stage 2.

Question 3

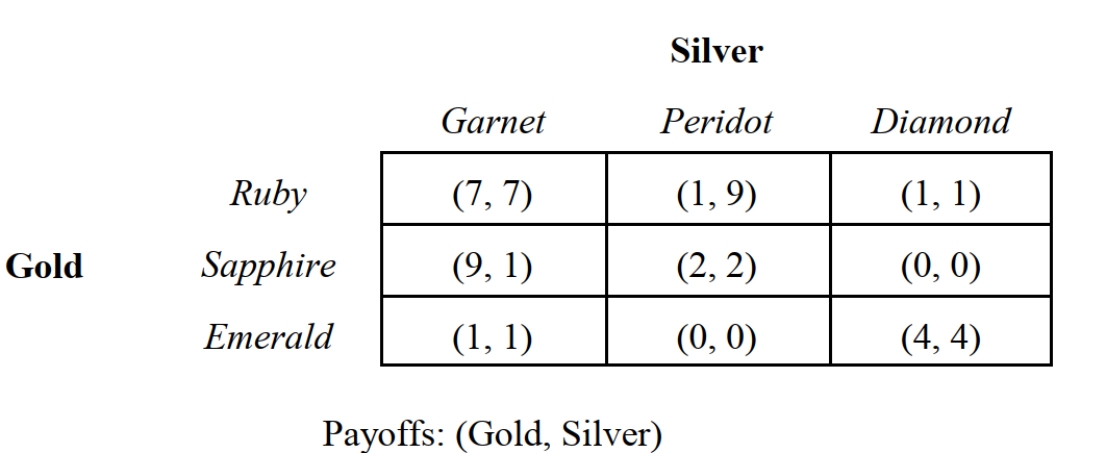
-Consider the two-stage game depicted in Figure 5.3 involving two companies that enter into an agreement to maximize total profits. The payoffs in this game are in millions of dollars. Gold's optimal strategy is to:

A) Play Ruby in stage 1 and stage 2.
B) Play Ruby in stage 1 and play Sapphire in stage 2.
C) Play Ruby in stage 1 and Emerald in stage 2.
D) Play Emerald in stage 1 and stage 2.
E) Play Emerald in stage 1 and play Ruby in stage 2.

Answer 3

Play Emerald in stage 1 and stage 2.

Question 4

-Consider the two-stage game depicted in Figure 5.3 involving two companies that enter into an agreement to maximize total profits. The payoffs in this game are in millions of dollars. Silver's optimal strategy is to:

A) Play Garnet in stage 1 and stage 2.
B) Play Garnet in stage 1 and play Peridot in stage 2.
C) Play Garnet in stage 1 and Diamond in stage 2.
D) Play Diamond in stage 1 and stage 2.
E) Play Diamond in stage 1 and play Garnet in stage 2.

Question 5

A strategic move is:

A) Another name for strategy in a one-time static game.
B) A rival's countermove.
C) An attempt by one player to alter the behavior of a rival.
D) Only successful if a player has a last-mover advantage.
E) Only successful in prisoner dilemma type games.

Question 6

The end-of-game problem:

A) Arises in finitely-repeated games with an uncertain end.
B) Occurs when each stage of a finitely-repeated game with a certain end effectively becomes the last stage.
C) Means that trigger strategies are enforceable.
D) Occurs when players make a move in the last stage of a finitely-repeated game that is different from the move made in the first stage of the game.
E) None of the above are correct.

Question 7

_____ is when a finitely-repeated game a certain end reduces to a series of one-time, static games.

A) A first-mover advantage
B) A trigger strategy
C) Tit-for-tat
D) End-of-game problem
E) Preemption

Question 8

The reason why a door-to-door salesman is able to sell a bogus cure for baldness, while the dishonest owner of a neighborhood barbershop cannot is because of the:

A) End-of-game problem.
B) First-mover advantage.
C) Prisoner's dilemma.
D) Reciprocity problem.
E) Food and Drug Administration.

Question 9

The probability that a two-player, repeated game comes to an end in each stage is 2. When 2 = 0, this game may be treated as:

A) A one-time game.
B) A finitely-repeated game with a certain end.
C) A finitely-repeated game with an uncertain end.
D) An infinitely-repeated game.
E) Answers a and b are correct.

Question 10

The probability that a two-player, repeated game comes to an end in each stage is 2. When 2 = 1, this game may be treated as:

A) A one-time game.
B) A finitely-repeated game with a certain end.
C) A finitely-repeated game with an uncertain end.
D) An infinitely-repeated game.
E) Answers a and b are correct.

Question 11

The probability that a two-player, repeated game comes to an end in each stage is 2. When 0 < 2 < 1, this game may be treated as:

A) A one-time game.
B) A finitely-repeated game with a certain end.
C) A finitely-repeated game with an uncertain end.
D) An infinitely-repeated game.
E) Answers a and b are correct.

Question 12

-Consider the noncooperative oil-drilling game depicted in Figure 5.4 in which payoffs are in millions of dollars. If this game is played five times, the Nash equilibrium strategy profile in the first round is:

A) {Narrow, Narrow}.
B) {Narrow, Wide}.
C) {Wide, Narrow}.
D) {Wide, Wide}.

Question 13

-Consider the noncooperative oil-drilling game depicted in Figure 5.4 in which payoffs are in millions of dollars. If this game is played five times, the Nash equilibrium strategy profile in the second round is:

A) {Narrow, Narrow}.
B) {Narrow, Wide}.
C) {Wide, Narrow}.
D) {Wide, Wide}.

Question 14

-Consider the noncooperative oil-drilling game depicted in Figure 5.4 in which payoffs are in millions of dollars. If this game is played five times, the Nash equilibrium strategy profile for this game in the fifth round is:

A) {Narrow, Narrow}.
B) {Narrow, Wide}.
C) {Wide, Narrow}.
D) {Wide, Wide}.

Question 15

-Consider the oil-drilling game depicted in Figure 5.4 in which payoffs are in millions of dollars. Suppose that this game is played repeatedly and the probability that the game will end in the next round is 10 percent and the discount rate is 25 percent. What is the present value of the stream of payoffs from not cooperating?

A) An amount between $85.7 and $85.8 million.
B) An amount between $113.7 and $113.8 million.
C) An amount between $185.7 and $185.8 million.
D) An amount between $210.8 and $210.9 million.
E) None of the above.

Question 16

-Consider the oil-drilling game depicted in Figure 5.4 in which payoffs are in millions of dollars. Suppose that this game is played repeatedly and the probability that the game will end in the next round is 10 percent and the discount rate is 25 percent. What is the present value of the stream of payoffs by cooperating?

A) An amount between $85.7 and $85.8 million.
B) An amount between $113.7 and $113.8 million.
C) An amount between $185.7 and $185.8 million.
D) An amount between $210.8 and $210.9 million.
E) None of the above.

Question 17

-Consider the oil-drilling game depicted in Figure 5.4 in which payoffs are in millions of dollars. Suppose that this game is played repeatedly and the probability that the game will end in the next round is 10 percent and the discount rate is 25 percent. What is the present value of the stream of payoffs from defection?

A) An amount between $95.7 and $95.8 million.
B) An amount between $114.7 and $114.8 million.
C) An amount between $169.7 and $169.8 million.
D) An amount between $182.6 and $182.7 million.
E) None of the above.

Question 18

-Consider the oil-drilling game depicted in Figure 5.4 in which payoffs are in millions of dollars. Suppose that this game is played repeatedly and the probability that the game will end in the next round is 15 percent. At what discount rate are the players indifferent between cooperating and defecting?

A) 20 percent.
B) 27.5 percent.
C) 32.75 percent.
D) 45 percent.
E) None of the above.

Question 19

-Consider the oil-drilling game depicted in Figure 5.4 in which payoffs are in millions of dollars. Suppose that this game is played repeatedly and the probability that the game will be played in the next round is 20 percent. At what discount rate are the players indifferent between cooperating and defecting?

A) 25 percent.
B) 27.5 percent.
C) 32.75 percent.
D) 45 percent.
E) None of the above.

Question 20

-Consider the oil-drilling game depicted in Figure 5.4 in which payoffs are in millions of dollars. Suppose that this game is played repeatedly and the discount rate is 25 percent. What is the probability that the game will end in the next stage will a player be indifferent between cooperating and defecting?

A) Around 10 percent.
B) Around 15 percent.
C) Around 17 percent.
D) Around 21 percent.
E) None of the above.

Question 21

-Consider the oil-drilling game depicted in Figure 5.4 in which payoffs are in millions of dollars. Suppose that this game is played repeatedly and the discount rate is 40 percent. What is the probability that the game will end in the next stage will a player be indifferent between cooperating and defecting?

A) Around 7 percent.
B) Around 10 percent.
C) Around 12 percent.
D) Around 15 percent.
E) None of the above.

Question 22

-Consider the pricing game depicted in Figure 5.5 in which the payoffs are in millions of dollars. If this game is played seven times, the Nash equilibrium strategy profile in the first stage is:

A) {Low price, Low price}.
B) {Low price, High price}.
C) {High price, Low price}.
D) {High price, High price}.

Question 23

-Consider the pricing game depicted in Figure 5.5 in which the payoffs are in millions of dollars. If this game is played three times, the Nash equilibrium strategy profile in the second stage is:

A) {Low price, Low price}.
B) {Low price, High price}.
C) {High price, Low price}.
D) {High price, High price}.

Question 24

-Consider the pricing game depicted in Figure 5.5 in which payoffs are in millions of dollars. Suppose that this game is played repeatedly and the probability that the game will end in the next stage is 20 percent and the discount rate is 20 percent. What is the present value of the stream of payoffs by not cooperating?

A) $8 million.
B) $12 million.
C) $18 million.
D) $30 million.
E) $108 million.

Question 25

-Consider the pricing game depicted in Figure 5.5 in which payoffs are in millions of dollars. Suppose that this game is played repeatedly and the probability that the game will end in the next stage is 20 percent and the discount rate is 20 percent. What is the present value of the stream of payoffs by cooperating?

A) $8 million.
B) $12 million.
C) $18 million.
D) $30 million.
E) $108 million.

Question 26

-Consider the pricing game depicted in Figure 5.5 in which payoffs are in millions of dollars. Suppose that this game is played repeatedly and the probability that the game will end in the next stage is 20 percent and the discount rate is 20 percent. What is the present value of the stream of future payoffs if either firm defects?

A) $8 million.
B) $12 million.
C) $18 million.
D) $30 million.
E) $108 million.

Question 27

-Consider the pricing game depicted in Figure 5.5 in which payoffs are in millions of dollars. Suppose that this game is played repeatedly and the probability that the game will end in the next stage is 1 percent. For what discount rate will a firm be indifferent between cooperating and defecting?

A) 2.5 percent.
B) 4.25 percent.
C) 5.6 percent.
D) 8.5 percent.
E) 10.25 percent.

Question 28

-Consider the pricing game depicted in Figure 5.5 in which payoffs are in millions of dollars. Suppose that this game is played repeatedly and the probability that the game will end in the next stage is 5 percent. For what discount rate will a firm be indifferent between cooperating and defecting?

A) 1.33 percent.
B) 1.67 percent.
C) 2.33 percent.
D) 2.67 percent.
E) 3.33 percent.

Question 29

-Consider the pricing game depicted in Figure 5.5 in which payoffs are in millions of dollars. Suppose that this game is played repeatedly and the discount rate is 5 percent. What is the probability that the game will end if the players are indifferent between cooperating and defecting?

A) Around 1.6 percent.
B) Around 2.5 percent.
C) Around 3.7 percent.
D) Around 4.5 percent.
E) Around 5.2 percent.

Question 30

-Consider the pricing game depicted in Figure 5.5 in which payoffs are in millions of dollars. Suppose that this game is played repeatedly and the discount rate is 1 percent. What is the probability that the game will end if the players are indifferent between cooperating and defecting?

A) Around 1.3 percent.
B) Around 3.3 percent.
C) Around 5.3 percent.
D) Around 7.6 percent.
E) None of the above.

Question 31

Tit-for-tat:

A) Is similar to backward induction.
B) Is an enforcement mechanism in repeated games where cooperation is possible.
C) Is the same thing as a scorched-earth policy.
D) Results in minimax payoffs.
E) None of the above.

Question 32

A tit-for-tat strategy is effective because it is:

A) Fair, balanced, transparent, and provocative.
B) Fair, transparent, provocative, and forgiving.
C) Transparent, provocative, balanced, and affable.
D) Balanced, transparent, provocative, and forgiving.
E) None of the above.

Question 33

A tit-for-tat strategy is effective because it is:

A) Transparent, balanced, affable, and provocative.
B) Fair, transparent, provocative, and forgiving.
C) Transparent, provocative, balanced, and affable.
D) Transparent, affable, provocative, and forgiving.
E) Transparent, fair, balanced, and provocative.

Question 34

The problem with a tit-for-tat strategy is that:

A) Players may misinterpret the moves or intentions of rivals.
B) It is not easy to understand.
C) It rules out the possibility of cooperation between and among players.
D) All of the above.
E) None of the above.

Question 35

For preemption to be successful:

A) It must give the initiating player a last-mover advantage.
B) It must give the initiating player a first-mover advantage.
C) The initiating player must have a dominant strategy.
D) A static game must have a unique Nash equilibrium.
E) The initiating player must use a maximin-regret decision rule.

Question 36

A player who can credibly commit to a strategy before a rival:

A) Has a dominant strategy.
B) Has a last-mover advantage.
C) Is in a strategically dominant position
D) Has a first-mover advantage.
E) Is able to transform a dynamic game into a static game.

Question 37

An example of preemption is:

A) Tit-for-tat.
B) Burning bridges.
C) Scorched earth.
D) Closing doors.
E) Answers a and c are correct.

Question 38

A scorched earth policy is an example of a:

A) Strategic move.
B) First-mover advantage.
C) Dominant strategy.
D) Weakly dominated strategy.
E) Guarantee.

Question 39

A scorched earth policy is a:

A) Strategic move.
B) Variation of tit-for-tat.
C) Form of preemption.
D) Answers a and c are correct.
E) All of the above are correct.

Question 40

In the text, the publishing company Houghton Mifflin was able to thwart Western Pacific's takeover bid by threatening to release its best-selling authors from their contractual obligations. This is an example of:

A) Tit-for-tat.
B) Burning bridges.
C) Scorched earth.
D) Dirty pool.
E) Answers a, b and c are correct.