Deck 6: Mixing Pure Strategies

Question 1

In a zero-sum game with pure strategies:

A) The payoffs may be different, but must add up to zero.
B) The gain by one player is exactly equal to the loss of the other player.
C) A Nash equilibrium can always be found using the maximin decision rule.
D) A Nash equilibrium can always be found using a minimax regret decision rule.
E) Must have a focal-point equilibrium.

Answer 1

The gain by one player is exactly equal to the loss of the other player.

Question 2

A two-player, two-strategy, noncooperative, zero-sum, static game has _____ Nash equilibria.

A) 0
B) 1
C) 2
D) 3
E) 4

Answer 2

0

Question 3

In the Sink-the-Battleship Game:

A) Both combatants had a dominant pure strategy.
B) One combatant with a dominant strategy, but the other combatant did not.
C) Neither combatant had a dominant strategy, even after dominated strategies were eliminated.
D) There were non-zero-sum payoffs.
E) None of the above.

Answer 3

Neither combatant had a dominant strategy, even after dominated strategies were eliminated.

Question 4

The Sink-the-Battleship Game:

A) Does not have a Nash equilibria in pure strategies. The best way to choose a strategy is to flip a coin after all dominated strategies were eliminated.
B) Has a unique Nash equilibrium in pure strategies. Both combatants have a dominant strategy.
C) Has multiple Nash equilibria in mixed strategies. Both combatants have dominated strategies.
D) Has two Nash equilibria in pure strategies, even though neither side had a dominant strategy.
E) None of the above are correct.

Question 5

In a two-player, zero-sum, noncooperative, simultaneous-move, one-time games:

A) Both players attempt to maximize the other player's minimum payoff, while minimizing their own maximum payoff.
B) Both players attempt to maximize the other player's maximum payoff, while minimizing their own minimum payoff.
C) Both players attempt to minimize the other player's minimum payoff, while maximizing their own maximum payoff.
D) Both players attempt to minimize the other player's maximum payoff, while maximizing their own minimum payoff.
E) None of the above are correct.

Question 6

Frans asked his mother, Greta, to bake him an apple pie. After baking the pie, Greta tells Frans to slice the pie any way he likes, but that he must give his brother, Hans, the first choice of slices. The only other condition is that the slices must be divided into quarters. The most likely Nash equilibrium strategy profile for this game is:

A) {1/4 pie, 3/4 pie}.
B) {3/4 pie, 1/4 pie}.
C) {1/2 pie, 1/2 pie}.
D) {Whole pie, 0}.
E) {0, Whole pie}.

Question 7

Frans asked his mother, Greta, to bake him an apple pie. After baking the pie, Greta tells Frans to slice the pie any way he likes, but that he must give his brother, Hans, the first choice of slices. The only other condition is that the slices must be divided into quarters. The most likely guiding principle for determining the Nash equilibrium strategy profile for this game is the:

A) fairness principle.
B) equity rule.
C) minimax theorem.
D) prisoner's dilemma.
E) conventional wisdom corollary.

Question 8

A pure strategy is:

A) An incomplete and random game plan.
B) A complete and random game plan.
C) An incomplete and nonrandom game plan.
D) A complete and nonrandom game plan.
E) None of the above. Pure strategies involve an imperfect game plan.

Question 9

-Suppose that a football team is 3 points behind and faces a fourth down and goal to go with seconds remaining on the clock. The offense can either pass or run the ball. The defense can either defend against the pass or defend against the run. Figure 6.1 summarizes the probabilities of winning or losing the game from any combination of strategy profiles. The dominant pure strategy for the defense is to:

A) Defend against the run.
B) Defend against the pass.
C) Flip a coin and choose a play at random.
D) There is not enough information to answer this question.
E) None of the above.

Question 10

-Consider the game in Figure 6.1. The optimal mixing rule for the offense is:

A) Randomly pass the ball 50 percent of the time.
B) Randomly run the ball 50 percent of the time.
C) Randomly defend against the pass 50 percent of the time.
D) Randomly defend against the run 50 percent of the time.
E) Answers a and b are correct.

Question 11

-Consider the game in Figure 6.1. The optimal mixing rule for the defense is:

A) Randomly pass the ball 50 percent of the time.
B) Randomly run the ball 50 percent of the time.
C) Randomly defend against the pass 50 percent of the time.
D) Randomly defend against the run 50 percent of the time.
E) Answers c and d are correct.

Question 12

-Consider the game in Figure 6.1. The dominant strategy for the offense is to:

A) Run the ball.
B) Pass the ball.
C) Flip a coin and choose an offensive play at random.
D) This game does not have a dominant strategy mixed strategies.
E) There is not enough information to answer this question.

Question 13

-Consider the game in Figure 6.1. What is the success rate of the defense if the offense adopts its optimal mixing rule?

A) 25 percent.
B) 50 percent.
C) 75 percent.
D) 100 percent.
E) None of the above.

Question 14

-Consider the game in Figure 6.1. What is the success rate of the offense if the defense adopts its optimal mixing rule?

A) 25 percent.
B) 50 percent.
C) 75 percent.
D) 100 percent.
E) None of the above.

Question 15

-Suppose that a football team is down by 5 points and faces a 4th down with 1 yard to go and 1 second left on the clock. The offense can either run or pass the ball. The defense can either defend against the run or the pass. Refer to Figure 6.2 summarizes the probabilities of each team winning the game. The dominant pure strategy for the offense is:

A) Run the ball.
B) Pass the ball.
C) Pick a play at random with a higher probability of passing the ball.
D) Pick a play at random with a higher probability of running the ball.
E) None of the above.

Question 16

-Suppose that a football team is down by 5 points and faces a 4th down with 1 yard to go with 1 second left on the clock. The offense can either run or pass the ball. The defense can either defend against the run or the pass. Refer to Figure 6.2 summarizes the probabilities of each team winning the game. The pure-strategy Nash equilibrium for this game is:
I. {Pass, Pass}.
II. {Run, Run}.
III. {Run, Pass}.
IV. {Pass, Run}.
Which of the following is correct?

A) I only.
B) II only.
C) I and II only.
D) II and III only.
E) None of the above.

Question 17

-Suppose that a football team is down by 5 points and faces a 4th down with 1 yard to go and 1 second left on the clock. The offense can either run or pass the ball. The defense can either defend against the run or the pass. Refer to Figure 6.2 summarizes the probabilities of each team winning the game. The optimal mixing rule for the offense is:

A) Randomly pass the ball 3 out of 8 times.
B) Randomly run the ball 5 out of 8 times.
C) Randomly pass the ball 5 out of 8 times.
D) Randomly pass the ball 3 out of 13 times.
E) Randomly run the ball 8 out of 13 times.

Question 18

-Suppose that a football team is down by 5 points and faces a 4th down with 1 yard to go and 1 second left on the clock. The offense can either run or pass the ball. The defense can either defend against the run or the pass. Refer to Figure 6.2 summarizes the probabilities of each team winning the game. Suppose that the offense adopts its optimal mixing rule. What is its success rate?

A) Around 33 percent.
B) Around 46 percent.
C) Around 54 percent.
D) Around 71 percent.
E) None of the above.

Question 19

-Suppose that a football team is down by 5 points and faces a 4th down with 1 yard to go and 1 second left on the clock. The offense can either run or pass the ball. The defense can either defend against the run or the pass. Refer to Figure 6.2 summarizes the probabilities of each team winning the game. The optimal mixing rule for the defense is:

A) Randomly defend against the pass 1 out of 8 times.
B) Randomly defend against the pass 7 out of 8 times.
C) Randomly defend against the pass 2 out of 8 times.
D) Randomly defend against the run 6 out of 8 times.
E) Randomly defend against the run 7 out of 9 times.

Question 20

-Suppose that a football team is down by 5 points and faces a 4th down with 1 yard to go and 1 second left on the clock. The offense can either run or pass the ball. The defense can either defend against the run or the pass. Refer to Figure 6.2 summarizes the probabilities of each team winning the game. Suppose that the defense adopts its optimal mixing rule. What is its success rate?

A) Around 29 percent.
B) Around 46 percent.
C) Around 54 percent.
D) Around 67 percent.
E) None of the above.

Question 21

-Suppose that a football team is down by 5 points and faces a 4th down with 1 yard to go and 1 second left on the clock. The offense can either run or pass the ball. The defense can either defend against the run or the pass. Refer to Figure 6.2 summarizes the probabilities of each team winning the game. The mixed-strategy Nash equilibrium for this game is:

A) Both teams pick their play at random with both more likely to focus on the run.
B) Both teams pick their play at random with both more likely to focus on the pass.
C) Both teams pick their play at random with the offense more likely to focus on the run and the defense more likely to focus on the pass.
D) Both teams pick their play at random with the offense more likely to focus on the pass and the defense more likely to focus on the run.
E) None of the above.

Question 22

-Suppose that a football team is down by 5 points and faces a 4th down with 1 yard to go and 1 second left on the clock. The offense can either run or pass the ball. The defense can either defend against the run or the pass. Refer to Figure 6.3 summarizes the probabilities of each team winning the game. The dominant pure strategy for the offense is:

A) Run the ball.
B) Pass the ball.
C) Pick a play at random with a higher probability of passing the ball.
D) Pick a play at random with a higher probability of running the ball.
E) None of the above.

Question 23

-Suppose that a football team is down by 5 points and faces a 4th down with 1 yard to go and 1 second left on the clock. The offense can either run or pass the ball. The defense can either defend against the run or the pass. Refer to Figure 6.3 summarizes the probabilities of each team winning the game. The dominant pure strategy for the defense is:

A) Defend against the run.
B) Defend against the pass.
C) Pick a play at random with a higher probability of defending against the pass.
D) Pick a play at random with a higher probability of defending against the run.
E) None of the above.

Question 24

-Suppose that a football team is down by 5 points and faces a 4th down with 1 yard to go and 1 second left on the clock. The offense can either run or pass the ball. The defense can either defend against the run or the pass. Refer to Figure 6.3 summarizes the probabilities of each team winning the game. The optimal mixing rule for the offense is:

A) Randomly pass 5 out of 9 times.
B) Randomly run 4 out of 9 times.
C) Randomly pass 2 out of 7 times.
D) Randomly run 5 out of 7 times.
E) Both c and d are correct.

Question 25

-Suppose that a football team is down by 5 points and faces a 4th down with 1 yard to go and 1 second left on the clock. The offense can either run or pass the ball. The defense can either defend against the run or the pass. Refer to Figure 6.3 summarizes the probabilities of each team winning the game. Suppose that both players adopt its optimal mixing rule. What is the success rate of the defense?

A) Around 39 percent.
B) Around 48 percent.
C) Around 55 percent.
D) Around 75 percent.
E) None of the above.

Question 26

-Suppose that a football team is down by 5 points and faces a 4th down with 1 yard to go and 1 second left on the clock. The offense can either run or pass the ball. The defense can either defend against the run or the pass. Refer to Figure 6.3 summarizes the probabilities of each team winning the game. The optimal mixing rule for the defense is:

A) Randomly defend against the pass 4 out of 11 times.
B) Randomly defend against the pass 4 out of 7 times.
C) Randomly defend against the pass 3 out of 11 times.
D) Randomly defend against run 7 out of 11 times.
E) Both a and d are correct.

Question 27

-Suppose that a football team is down by 5 points and faces a 4th down with 1 yard to go and 1 second left on the clock. The offense can either run or pass the ball. The defense can either defend against the run or the pass. Refer to Figure 6.3 summarizes the probabilities of each team winning the game. Suppose that both players adopts its optimal mixing rule. What is the success rate of the offense?

A) Around 25 percent.
B) Around 45 percent.
C) Around 52 percent.
D) Around 61 percent.
E) None of the above.

Question 28

-Suppose that a football team is down by 5 points and faces a 4th down with 1 yard to go and 1 second left on the clock. The offense can either run or pass the ball. The defense can either defend against the run or the pass. Refer to Figure 6.3 summarizes the probabilities of each team winning the game. The mixed-strategy Nash equilibrium for this game is:

A) Both teams pick their play at random with both more likely to focus on the run.
B) Both teams pick their play at random with both more likely to focus on the pass.
C) Both teams pick their play at random with the offense more likely to focus on the run and the defense more likely to focus on the pass.
D) Both teams pick their play at random with the offense more likely to focus on the pass and the defense more likely to focus on the run.
E) None of the above.

Question 29

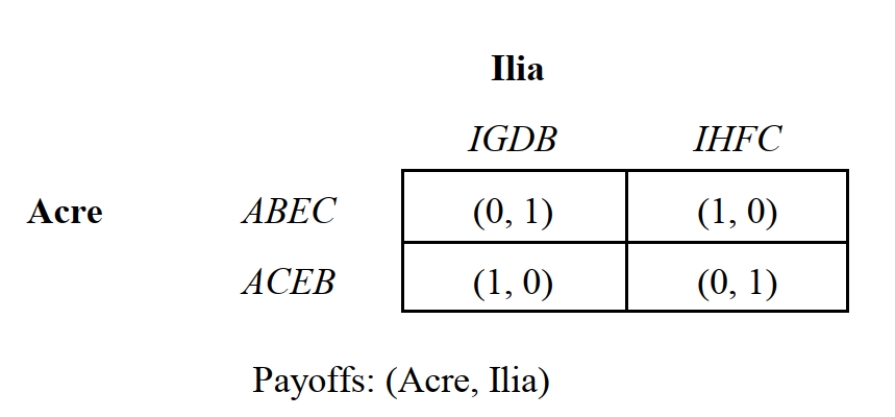
-Consider the reduced form of the Sink-the-Battleship Game depicted in Figure 6.4 where 1 designates a "hit" and 0 designates a "miss." The pure-strategy Nash equilibrium for this game is:
I. {ABEC, IGDB}.
II. {ACEB, IHFC}.
III. {ABEC, IHFC}.
IV. {ACEB, IHFC}.
Which of the following is correct?

A) I only.
B) II only.
C) I and II only.
D) II and III only.
E) None of the above.

Question 30

-Consider the reduced form of the Sink-the-Battleship Game depicted in Figure 6.4 where 1 designates a "hit" and 0 designates a "miss." Acre's optimal mixing rule is to program its computer to:

A) Randomly select IGDB one out of two times.
B) Randomly select IHFC one out of two times.
C) Randomly select IGDB one out of 3 times.
D) Randomly select IHFC one out of 3 times.
E) None of the above.

Question 31

-Consider the reduced form of the Sink-the-Battleship Game depicted in Figure 6.4 where 1 designates a "hit" and 0 designates a "miss." Suppose that Acre adopts its optimal mixing rule. Its success rate will be:

A) 25 percent.
B) 50 percent.
C) 75 percent.
D) 100 percent.
E) None of the above.

Question 32

-Consider the reduced form of the Sink-the-Battleship Game depicted in Figure 6.4 where 1 designates a "hit" and 0 designates a "miss." Ilia's optimal mixing rule is to program its computer to:

A) Randomly select IGDB one out of two times.
B) Randomly select IHFC one out of two times.
C) Randomly select IGDB one out of 3 times.
D) Randomly select IHFC one out of 3 times.
E) Answers a and b are correct.

Question 33

-Consider the reduced form of the Sink-the-Battleship Game depicted in Figure 6.4 where 1 designates a "hit" and 0 designates a "miss." Suppose that Ilia adopts its optimal mixing rule. Its success rate will be:

A) 25 percent.
B) 50 percent.
C) 75 percent.
D) 100 percent.
E) None of the above.

Question 34

-Suppose that two individuals play a game of tennis. The situation depicted in Figure 6.5 summarizes the probabilities that the receiver will successfully return a serve that is directed to his backhand or forehand. The server's optimal mixing rule is:

A) Randomly serve to the forehand 3 out of 14 times.
B) Randomly serve to the forehand 3 out of 7 times.
C) Randomly serve to the backhand 3 out of 14 times.
D) Randomly serve to the backhand 3 out of 7 times.
E) None of the above.

Question 35

-Suppose that two individuals play a game of tennis. The situation depicted in Figure 6.5 summarizes the probabilities that the receiver will successfully return a serve that is directed to his backhand or forehand. Suppose that both players adopt his or her optimal mixing rule. The receiver's success rate will be:

A) Around 22 percent.
B) Around 48 percent.
C) Around 53 percent.
D) Around 58 percent.
E) Around 65 percent.

Question 36

-Suppose that two individuals play a game of tennis. The situation depicted in Figure 6.5 summarizes the probabilities that the receiver will successfully return a serve that is directed to his backhand or forehand. The receiver's optimal mixing rule is:

A) Randomly return to the forehand 13 out of 21 times.
B) Randomly return to the backhand 12 out of 21 times.
C) Randomly return to the forehand 7 out of 12 times.
D) Randomly return to the backhand 16 out of 23 times.
E) None of the above.

Question 37

-Suppose that two individuals play a game of tennis. The situation depicted in Figure 6.5 summarizes the probabilities that the receiver will successfully return a serve that is directed to his backhand or forehand. Suppose that both players adopt his or her optimal mixing rule. The servers's success rate will be:

A) Around 29 percent.
B) Around 39 percent.
C) Around 43 percent.
D) Around 52 percent.
E) Around 78 percent.

Question 38

-Suppose that two individuals play a game of tennis. The situation depicted in Figure 6.5summarizes the probabilities that the receiver will successfully return a serve that isdirected to his backhand or forehand. The mixed-strategy Nash equilibrium for this game is:

A) Both tennis players moving randomly but emphasizing the forehand.
B) Both tennis players moving randomly but emphasizing the backhand.
C) Both tennis players moving randomly with the server emphasizing the forehand and the receiver emphasizing the backhand.
D) Both tennis players moving randomly with the server emphasizing the backhand and the receiver emphasizing the forehand.
E) None of the above.

Question 39

-Consider the oil-drilling game in Figure 6.6. Payoffs are in millions of dollars. GLOMAR's optimal mixing rule is:

A) Randomly drill a narrow well 4 out of 5 times.
B) Randomly drill a wide well 1 out of 5 times.
C) Randomly drill a narrow well 3 out of 4 times.
D) Randomly drill a narrow well 6 out of 15 times.
E) Answers a and b are correct.

Question 40

-Consider the oil-drilling game in Figure 6.6. Payoffs are in millions of dollars. If both oil-drilling companies adopt its optimal mixing rule, PETROX's expected payoff is:

A) $24 million.
B) $36 million.
C) $42 million.
D) $58 million.
E) None of the above.

Question 41

-Consider the oil-drilling game in Figure 6.6. Payoffs are in millions of dollars. PETROX's optimal mixing rule is:

A) Randomly drill a narrow well 4 out of 5 times.
B) Randomly drill a wide well 1 out of 5 times.
C) Randomly drill a narrow well 3 out of 4 times.
D) Randomly drill a narrow well 6 out of 15 times.
E) Answers a and b are correct.

Question 42

-Consider the oil-drilling game in Figure 6.6. Payoffs are in millions of dollars. If both oil-drilling companies adopt its optimal mixing rule, GLOMAR's expected payoff is:

A) $42 million.
B) $58 million.
C) $64 million.
D) $76 million.
E) None of the above.

Question 43

-Consider the oil-drilling game in Figure 6.6. The mixed-strategy Nash equilibrium for this game is:

A) Both companies randomly drill emphasizing narrow wells.
B) Both companies randomly drill emphasizing wide wells.
C) Both companies to randomly drill with PETROX emphasizing wide wells and GLOMAR emphasizing narrow wells.
D) Both companies to randomly drill with PETROX emphasizing narrow wells and GLOMAR emphasizing wide wells.
E) None of the above.

Question 44

The Nash equilibrium existence theorem guarantees that:

A) A pure-strategy Nash equilibrium always exists for static games with a finite number of players and pure strategies.
B) A mixed-strategy Nash equilibrium only exists for zero-sum games.
C) A mixed-strategy Nash equilibrium exists for any game with a finite number of players and pure strategies.
D) mixed-strategy Nash equilibrium exists for games in which one player has a dominant strategy.
E) Answers c and d are correct.

Question 45

-Professor Nash teaches game theory at Gigantic State University (GSU). Just prior to the final exam, Professor Nash announces that students who score in the top half of the class will receive an A, while students who score in the bottom half will receive an F.There are just two types of students at GSU: Egg heads and knot heads. The students must decide whether to study for the final exam or not study and party. The payoffs for this game are summarized in Figure 6.7. If larger payoffs are preferred, which group has a dominant pure strategy?

A) Egg heads.
B) Knot heads.
C) Both groups.
D) Neither group.
E) This question cannot be answered without additional information

Question 46

-Professor Nash teaches game theory at Gigantic State University (GSU). Just prior to the final exam, Professor Nash announces that students who score in the top half of the class will receive an A, while students who score in the bottom half will receive an F. There are just two types of students at GSU: Egg heads and knot heads. The students must decide whether to study for the final exam or not study and party. The payoffs for this game are summarized in Figure 6.7. If larger payoffs are preferred, which group has a dominant mixed strategy?

A) Egg heads.
B) Knot heads.
C) Both groups.
D) Neither group.
E) This question cannot be answered without additional information.

Question 47

-Professor Nash teaches game theory at Gigantic State University (GSU). Just prior to the final exam, Professor Nash announces that students who score in the top half of the class will receive an A, while students who score in the bottom half will receive an F. There are just two types of students at GSU: Egg heads and knot heads. The students must decide whether to study for the final exam or not study and party. The payoffs for this game are summarized in Figure 6.7. If larger payoffs are preferred, the mixed-strategy Nash equilibrium strategy profile for this game is:

A) {Study, Study}.
B) {Party, Study}.
C) {Study, Party}.
D) {Party, Party}.
E) None of the above pure strategy profiles are correct.

Question 48

-Professor Nash teaches game theory at Gigantic State University (GSU). Just prior to the final exam, Professor Nash announces that students who score in the top half of the class will receive an A, while students who score in the bottom half will receive an F. There are just two types of students at GSU: Egg heads and knot heads. The students must decide whether to study for the final exam or not study and party. The payoffs for this game are summarized in Figure 6.7. What is the Knot Head's optimal mixing rule?

A) Randomly study 2 out of 7 times.
B) Randomly party 3 out of 7 times.
C) Randomly study 3 our of 4 times.
D) Randomly party 1 out of 5 times.
E) Answers a and b are correct.

Question 49

-Professor Nash teaches game theory at Gigantic State University (GSU). Just prior to the final exam, Professor Nash announces that students who score in the top half of the class will receive an A, while students who score in the bottom half will receive an F. There are just two types of students at GSU: Egg heads and knot heads. The students must decide whether to study for the final exam or not study and party. The payoffs for this game are summarized in Figure 6.7. What is the Egg Head's optimal mixing rule?

A) Randomly study 4 out of 9 times.
B) Randomly party 5 out of 13 times.
C) Randomly study 7 our of 10 times.
D) Randomly party 3 out of 8 times.
E) Answers c and d are correct.

Question 50

-Professor Nash teaches game theory at Gigantic State University (GSU). Just prior to the final exam, Professor Nash announces that students who score in the top half of the class will receive an A, while students who score in the bottom half will receive an F. There are just two types of students at GSU: Egg heads and knot heads. The students must decide whether to study for the final exam or not study and party. The payoffs for this game are summarized in Figure 6.7. If both groups adopt is optimal mixing rule, the Egg Head's expected payoff is:

A) 3.
B) 8.
C) 12.
D) 36.
E) None of the above.

Question 51

-Professor Nash teaches game theory at Gigantic State University (GSU). Just prior to the final exam, Professor Nash announces that students who score in the top half of the class will receive an A, while students who score in the bottom half will receive an F. There are just two types of students at GSU: Egg heads and knot heads. The students must decide whether to study for the final exam or not study and party. The payoffs for this game are summarized in Figure 6.7. If both groups adopt is optimal mixing rule, the Knot Head's expected payoff is:

A) 3.
B) 8.
C) 12.
D) 36.
E) None of the above.