Exam 6: Mixing Pure Strategies
Exam 1: Introduction to Game Theory35 Questions
Exam 2: Noncooperative, One-Time, Static Games86 Questions
Exam 3: Focal-Point and Evolutionary Equilibria32 Questions
Exam 4: Infinitely-Repeated, Static Games37 Questions
Exam 5: Finitely-Repeated, Static Games40 Questions
Exam 6: Mixing Pure Strategies51 Questions
Exam 7: Static Games With Continuous Strategies24 Questions
Exam 8: Imperfect Competition52 Questions
Exam 9: Perfect Competition and Monopoly33 Questions
Exam 10: Strategic Trade Policy35 Questions
Exam 11: Dynamic Games With Complete47 Questions
Exam 12: Bargaining54 Questions
Exam 13: Pure Strategies With Uncertain Payoffs65 Questions
Exam 14: Torts and Contracts45 Questions
Exam 15: Auctions44 Questions
Exam 16: Dynamic Games With Incomplete Information34 Questions
Select questions type
In a two-player, zero-sum, noncooperative, simultaneous-move, one-time games:
Free
(Multiple Choice)
4.9/5  (38)
(38)
Correct Answer:
D
 -Professor Nash teaches game theory at Gigantic State University (GSU). Just prior to the final exam, Professor Nash announces that students who score in the top half of the class will receive an A, while students who score in the bottom half will receive an F.There are just two types of students at GSU: Egg heads and knot heads. The students must decide whether to study for the final exam or not study and party. The payoffs for this game are summarized in Figure 6.7. If larger payoffs are preferred, which group has a dominant pure strategy?
-Professor Nash teaches game theory at Gigantic State University (GSU). Just prior to the final exam, Professor Nash announces that students who score in the top half of the class will receive an A, while students who score in the bottom half will receive an F.There are just two types of students at GSU: Egg heads and knot heads. The students must decide whether to study for the final exam or not study and party. The payoffs for this game are summarized in Figure 6.7. If larger payoffs are preferred, which group has a dominant pure strategy?
Free
(Multiple Choice)
4.8/5  (36)
(36)
Correct Answer:
D
 -Suppose that a football team is down by 5 points and faces a 4th down with 1 yard to go with 1 second left on the clock. The offense can either run or pass the ball. The defense can either defend against the run or the pass. Refer to Figure 6.2 summarizes the probabilities of each team winning the game. The pure-strategy Nash equilibrium for this game is:
I. {Pass, Pass}.
II. {Run, Run}.
III. {Run, Pass}.
IV. {Pass, Run}.
Which of the following is correct?
-Suppose that a football team is down by 5 points and faces a 4th down with 1 yard to go with 1 second left on the clock. The offense can either run or pass the ball. The defense can either defend against the run or the pass. Refer to Figure 6.2 summarizes the probabilities of each team winning the game. The pure-strategy Nash equilibrium for this game is:
I. {Pass, Pass}.
II. {Run, Run}.
III. {Run, Pass}.
IV. {Pass, Run}.
Which of the following is correct?
(Multiple Choice)
4.8/5  (36)
(36)
 -Consider the oil-drilling game in Figure 6.6. Payoffs are in millions of dollars. If both oil-drilling companies adopt its optimal mixing rule, GLOMAR's expected payoff is:
-Consider the oil-drilling game in Figure 6.6. Payoffs are in millions of dollars. If both oil-drilling companies adopt its optimal mixing rule, GLOMAR's expected payoff is:
(Multiple Choice)
4.9/5  (40)
(40)
 -Suppose that a football team is down by 5 points and faces a 4th down with 1 yard to go and 1 second left on the clock. The offense can either run or pass the ball. The defense can either defend against the run or the pass. Refer to Figure 6.3 summarizes the probabilities of each team winning the game. The dominant pure strategy for the offense is:
-Suppose that a football team is down by 5 points and faces a 4th down with 1 yard to go and 1 second left on the clock. The offense can either run or pass the ball. The defense can either defend against the run or the pass. Refer to Figure 6.3 summarizes the probabilities of each team winning the game. The dominant pure strategy for the offense is:
(Multiple Choice)
4.9/5  (36)
(36)
 -Consider the oil-drilling game in Figure 6.6. The mixed-strategy Nash equilibrium for this game is:
-Consider the oil-drilling game in Figure 6.6. The mixed-strategy Nash equilibrium for this game is:
(Multiple Choice)
4.9/5  (36)
(36)
 -Suppose that a football team is 3 points behind and faces a fourth down and goal to go with seconds remaining on the clock. The offense can either pass or run the ball. The defense can either defend against the pass or defend against the run. Figure 6.1 summarizes the probabilities of winning or losing the game from any combination of strategy profiles. The dominant pure strategy for the defense is to:
-Suppose that a football team is 3 points behind and faces a fourth down and goal to go with seconds remaining on the clock. The offense can either pass or run the ball. The defense can either defend against the pass or defend against the run. Figure 6.1 summarizes the probabilities of winning or losing the game from any combination of strategy profiles. The dominant pure strategy for the defense is to:
(Multiple Choice)
4.9/5  (37)
(37)
 -Suppose that a football team is down by 5 points and faces a 4th down with 1 yard to go and 1 second left on the clock. The offense can either run or pass the ball. The defense can either defend against the run or the pass. Refer to Figure 6.2 summarizes the probabilities of each team winning the game. Suppose that the defense adopts its optimal mixing rule. What is its success rate?
-Suppose that a football team is down by 5 points and faces a 4th down with 1 yard to go and 1 second left on the clock. The offense can either run or pass the ball. The defense can either defend against the run or the pass. Refer to Figure 6.2 summarizes the probabilities of each team winning the game. Suppose that the defense adopts its optimal mixing rule. What is its success rate?
(Multiple Choice)
4.8/5  (40)
(40)
 -Consider the oil-drilling game in Figure 6.6. Payoffs are in millions of dollars. GLOMAR's optimal mixing rule is:
-Consider the oil-drilling game in Figure 6.6. Payoffs are in millions of dollars. GLOMAR's optimal mixing rule is:
(Multiple Choice)
4.8/5  (41)
(41)
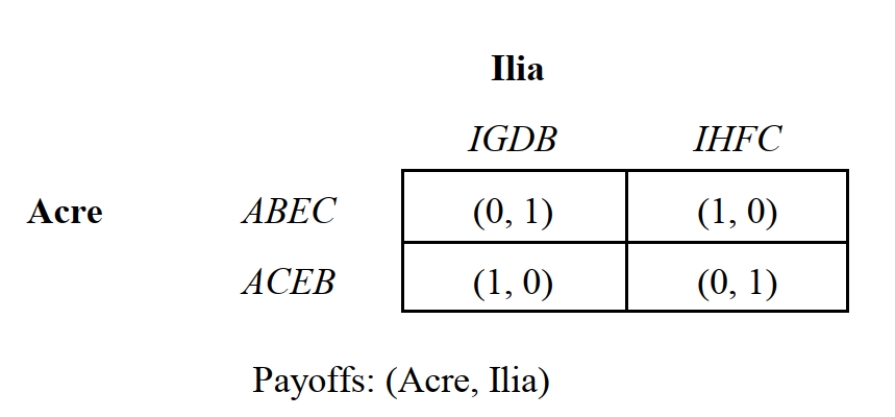 -Consider the reduced form of the Sink-the-Battleship Game depicted in Figure 6.4 where 1 designates a "hit" and 0 designates a "miss." Acre's optimal mixing rule is to program its computer to:
-Consider the reduced form of the Sink-the-Battleship Game depicted in Figure 6.4 where 1 designates a "hit" and 0 designates a "miss." Acre's optimal mixing rule is to program its computer to:
(Multiple Choice)
4.8/5  (37)
(37)
 -Professor Nash teaches game theory at Gigantic State University (GSU). Just prior to the final exam, Professor Nash announces that students who score in the top half of the class will receive an A, while students who score in the bottom half will receive an F. There are just two types of students at GSU: Egg heads and knot heads. The students must decide whether to study for the final exam or not study and party. The payoffs for this game are summarized in Figure 6.7. What is the Egg Head's optimal mixing rule?
-Professor Nash teaches game theory at Gigantic State University (GSU). Just prior to the final exam, Professor Nash announces that students who score in the top half of the class will receive an A, while students who score in the bottom half will receive an F. There are just two types of students at GSU: Egg heads and knot heads. The students must decide whether to study for the final exam or not study and party. The payoffs for this game are summarized in Figure 6.7. What is the Egg Head's optimal mixing rule?
(Multiple Choice)
4.7/5  (25)
(25)
 -Suppose that a football team is down by 5 points and faces a 4th down with 1 yard to go and 1 second left on the clock. The offense can either run or pass the ball. The defense can either defend against the run or the pass. Refer to Figure 6.3 summarizes the probabilities of each team winning the game. Suppose that both players adopt its optimal mixing rule. What is the success rate of the defense?
-Suppose that a football team is down by 5 points and faces a 4th down with 1 yard to go and 1 second left on the clock. The offense can either run or pass the ball. The defense can either defend against the run or the pass. Refer to Figure 6.3 summarizes the probabilities of each team winning the game. Suppose that both players adopt its optimal mixing rule. What is the success rate of the defense?
(Multiple Choice)
4.8/5  (24)
(24)
 -Consider the game in Figure 6.1. The optimal mixing rule for the defense is:
-Consider the game in Figure 6.1. The optimal mixing rule for the defense is:
(Multiple Choice)
4.8/5  (30)
(30)
 -Suppose that two individuals play a game of tennis. The situation depicted in Figure 6.5 summarizes the probabilities that the receiver will successfully return a serve that is directed to his backhand or forehand. The server's optimal mixing rule is:
-Suppose that two individuals play a game of tennis. The situation depicted in Figure 6.5 summarizes the probabilities that the receiver will successfully return a serve that is directed to his backhand or forehand. The server's optimal mixing rule is:
(Multiple Choice)
4.9/5  (36)
(36)
 -Consider the reduced form of the Sink-the-Battleship Game depicted in Figure 6.4 where 1 designates a "hit" and 0 designates a "miss." Ilia's optimal mixing rule is to program its computer to:
-Consider the reduced form of the Sink-the-Battleship Game depicted in Figure 6.4 where 1 designates a "hit" and 0 designates a "miss." Ilia's optimal mixing rule is to program its computer to:
(Multiple Choice)
4.8/5  (39)
(39)
 -Suppose that a football team is down by 5 points and faces a 4th down with 1 yard to go and 1 second left on the clock. The offense can either run or pass the ball. The defense can either defend against the run or the pass. Refer to Figure 6.3 summarizes the probabilities of each team winning the game. The optimal mixing rule for the offense is:
-Suppose that a football team is down by 5 points and faces a 4th down with 1 yard to go and 1 second left on the clock. The offense can either run or pass the ball. The defense can either defend against the run or the pass. Refer to Figure 6.3 summarizes the probabilities of each team winning the game. The optimal mixing rule for the offense is:
(Multiple Choice)
4.9/5  (40)
(40)
 -Consider the game in Figure 6.1. The optimal mixing rule for the offense is:
-Consider the game in Figure 6.1. The optimal mixing rule for the offense is:
(Multiple Choice)
4.8/5  (24)
(24)
Showing 1 - 20 of 51
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)