Deck 4: Vector Spaces
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/100
Play
Full screen (f)
Deck 4: Vector Spaces
1
Find the sum of the vectors 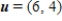 and
and 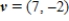 .
.
A)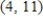
B)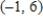
C)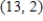
D)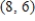
E)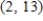
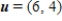 and
and 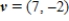 .
.A)
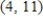
B)
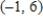
C)
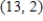
D)
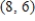
E)
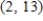
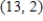
2
Find the vector v for which 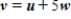 given that
given that 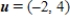 and
and 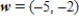 .
.
A)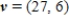
B)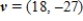
C)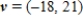
D)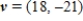
E)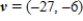
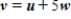 given that
given that 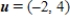 and
and 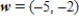 .
.A)
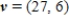
B)
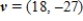
C)
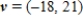
D)
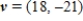
E)
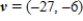
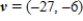
3
Let 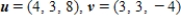 , and
, and 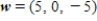 . Find
. Find 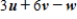 .
.
A)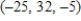
B)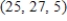
C)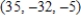
D)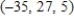
E)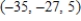
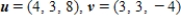 , and
, and 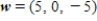 . Find
. Find 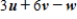 .
.A)
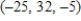
B)
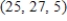
C)
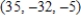
D)
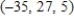
E)
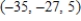
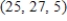
4
Which of the following vectors is the scalar multiple of 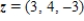
A)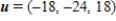
B)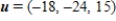
C)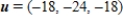
D)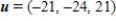
E)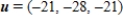
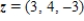
A)
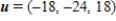
B)
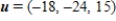
C)
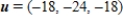
D)
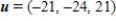
E)
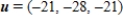

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
5
Provided 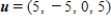 and
and 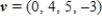 , solve
, solve 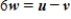 for w.
for w.
A)
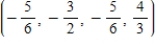
B)
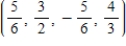
C)
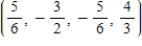
D)
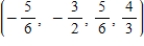
E)
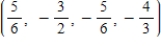
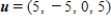 and
and 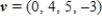 , solve
, solve 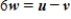 for w.
for w.A)
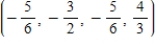
B)
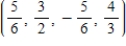
C)
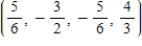
D)
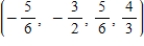
E)
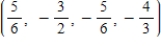

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
6
Provided that 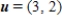 and
and 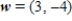 , write
, write 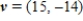 as a linear combination of u and w, if possible.
as a linear combination of u and w, if possible.
A)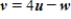
B)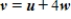
C)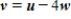
D)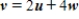
E) It is not possible to write v as a linear combination of u and w.
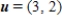 and
and 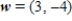 , write
, write 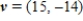 as a linear combination of u and w, if possible.
as a linear combination of u and w, if possible. A)
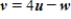
B)
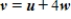
C)
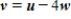
D)
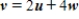
E) It is not possible to write v as a linear combination of u and w.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
7
Provided 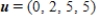 and
and 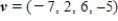 , find w such that
, find w such that 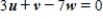 .
.
A)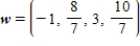
B)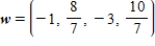
C)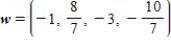
D)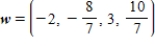
E)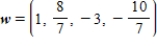
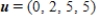 and
and 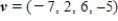 , find w such that
, find w such that 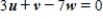 .
.A)
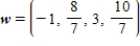
B)
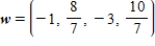
C)
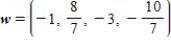
D)
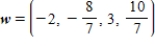
E)
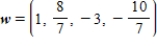

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
8
Provided that 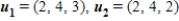 and
and 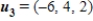 , write
, write 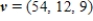 as a linear combination of
as a linear combination of 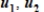 , and
, and  , if possible.
, if possible.
A)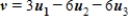
B)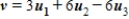
C)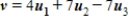
D)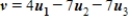
E) It is not possible to write v as a linear combination of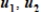 , and
, and  .
.
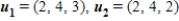 and
and 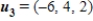 , write
, write 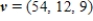 as a linear combination of
as a linear combination of 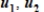 , and
, and  , if possible.
, if possible.A)
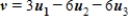
B)
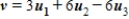
C)
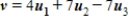
D)
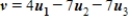
E) It is not possible to write v as a linear combination of
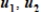 , and
, and  .
.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
9
Provide that 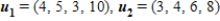 , and
, and 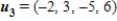 , write
, write 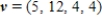 as a linear combination of
as a linear combination of 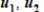 , and
, and  , if possible.
, if possible.
A)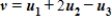
B)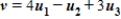
C)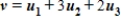
D)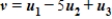
E) It is not possible to write v as a linear combination of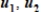 , and
, and  .
.
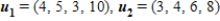 , and
, and 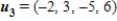 , write
, write 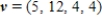 as a linear combination of
as a linear combination of 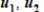 , and
, and  , if possible.
, if possible.A)
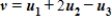
B)
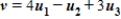
C)
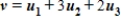
D)
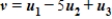
E) It is not possible to write v as a linear combination of
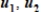 , and
, and  .
.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
10
Describe the zero vector (the additive identity) of the vector space 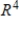 .
.
A) (0, 0, 0, 0, 0)
B) (0, 0, 0, 0)
C) (0, 0, 0, 0, 0, 0)
D) (0, 0)
E) (0, 0, 0)
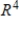 .
.A) (0, 0, 0, 0, 0)
B) (0, 0, 0, 0)
C) (0, 0, 0, 0, 0, 0)
D) (0, 0)
E) (0, 0, 0)

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
11
Describe the zero vector (the additive identity) of the vector space 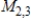 .
.
A)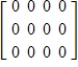
B)
C)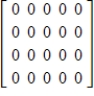
D)
E)
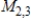 .
.A)
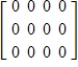
B)

C)

D)

E)


Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
12
Describe the zero vector (the additive identity) of the vector space 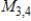 .
.
A)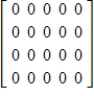
B)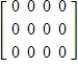
C)
D)
E)
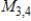 .
.A)

B)
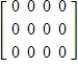
C)

D)

E)


Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
13
Describe the zero vector (the additive identity) of the vector space 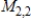 .
.
A)
B)
C)
D)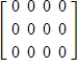
E)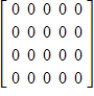
 .
.A)

B)

C)

D)
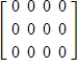
E)


Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
14
Describe the zero vector (the additive identity) of the vector space 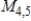 .
.
A)
B)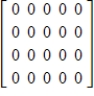
C)
D)
E)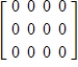
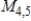 .
.A)

B)

C)

D)

E)
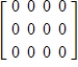

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
15
Describe the zero vector (the additive identity) of the vector space 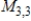 .
.
A)
B)
C)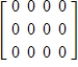
D)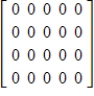
E)
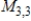 .
.A)

B)

C)
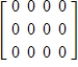
D)

E)


Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
16
Describe the zero vector (the additive identity) of the vector space 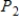 .
.
A)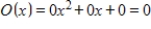
B)
C)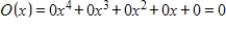
D)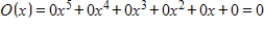
E)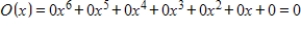
 .
. A)
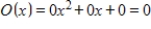
B)

C)
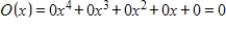
D)
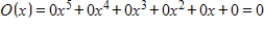
E)
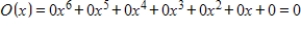

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
17
Describe the zero vector (the additive identity) of the vector space 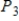 .
.
A)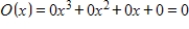
B)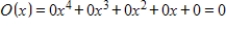
C)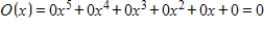
D)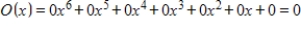
E)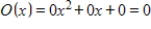
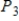 .
. A)
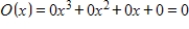
B)
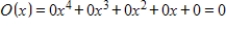
C)
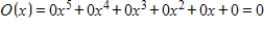
D)
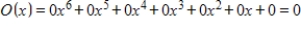
E)
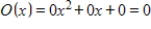

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
18
Describe the zero vector (the additive identity) of the vector space 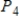 .
.
A)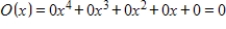
B)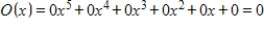
C)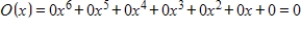
D)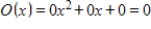
E)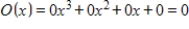
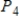 .
. A)
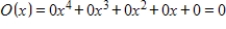
B)
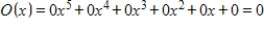
C)
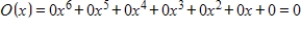
D)
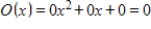
E)
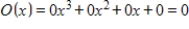

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
19
Describe the zero vector (the additive identity) of the vector space 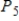 .
.
A)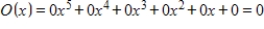
B)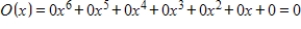
C)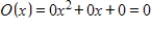
D)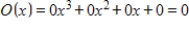
E)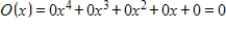
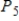 .
. A)
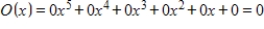
B)
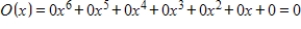
C)
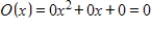
D)
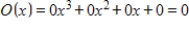
E)
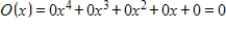

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
20
Describe the zero vector (the additive identity) of the vector space 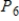 .
.
A)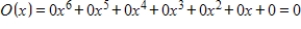
B)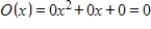
C)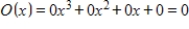
D)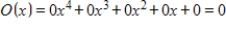
E)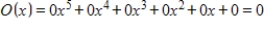
 .
. A)
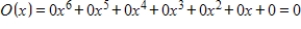
B)
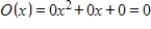
C)
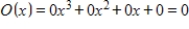
D)
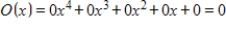
E)
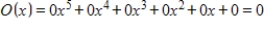

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
21
Determine whether the set, 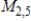 with the standard operations, is a vector space. If it is not, then determine the set of axioms that it fails.
with the standard operations, is a vector space. If it is not, then determine the set of axioms that it fails.
A) This set is not a vector space. It fails the following axioms.
Commutative property
Additive identity
Distributive property
B) This set is not a vector space. It fails the following axioms.
Scalar identity
Associative property
Distributive property
Additive identity
C) This set is a vector space. All ten vector space axioms hold.
D) This set is not a vector space. It fails the following axioms.
Additive identity
Additive inverse
Associative property
Scalar identity
E) This set is not a vector space. It fails the following axioms.
Closer under addition
Closer under scalar multiplication
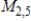 with the standard operations, is a vector space. If it is not, then determine the set of axioms that it fails.
with the standard operations, is a vector space. If it is not, then determine the set of axioms that it fails.A) This set is not a vector space. It fails the following axioms.
Commutative property
Additive identity
Distributive property
B) This set is not a vector space. It fails the following axioms.
Scalar identity
Associative property
Distributive property
Additive identity
C) This set is a vector space. All ten vector space axioms hold.
D) This set is not a vector space. It fails the following axioms.
Additive identity
Additive inverse
Associative property
Scalar identity
E) This set is not a vector space. It fails the following axioms.
Closer under addition
Closer under scalar multiplication

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
22
Determine whether the set of all first-degree polynomial functions as given below, whose graphs pass through the origin with the standard operations, is a vector space. If it is not, then determine the set of axioms that it fails. 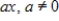
A) This set is not a vector space. It fails the following axioms.
Commutative property
Additive identity
Distributive property
B) This set is not a vector space. It fails the following axioms.
Scalar identity
Associative property
Distributive property
Additive identity
C) This set is not a vector space. It fails the following axioms.
Additive identity
Additive inverse
Associative property
Scalar identity
D) This set is a vector space. All ten vector space axioms hold.
E) This set is not a vector space. It fails the following axioms.
Closer under addition
Closer under scalar multiplication
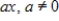
A) This set is not a vector space. It fails the following axioms.
Commutative property
Additive identity
Distributive property
B) This set is not a vector space. It fails the following axioms.
Scalar identity
Associative property
Distributive property
Additive identity
C) This set is not a vector space. It fails the following axioms.
Additive identity
Additive inverse
Associative property
Scalar identity
D) This set is a vector space. All ten vector space axioms hold.
E) This set is not a vector space. It fails the following axioms.
Closer under addition
Closer under scalar multiplication

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
23
Determine whether the set of all second-degree polynomial functions as given below, whose graphs pass through the origin with the standard operations, is a vector space. If it is not, then determine the set of axioms that it fails. 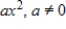
A) This set is not a vector space. It fails the following axioms.
Commutative property
Additive identity
Distributive property
B) This set is not a vector space. It fails the following axioms.
Scalar identity
Associative property
Distributive property
Additive identity
C) This set is not a vector space. It fails the following axioms.
Additive identity
Additive inverse
Associative property
Scalar identity
D) This set is a vector space. All ten vector space axioms hold.
E) This set is not a vector space. It fails the following axioms.
Closer under addition
Closer under scalar multiplication
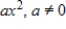
A) This set is not a vector space. It fails the following axioms.
Commutative property
Additive identity
Distributive property
B) This set is not a vector space. It fails the following axioms.
Scalar identity
Associative property
Distributive property
Additive identity
C) This set is not a vector space. It fails the following axioms.
Additive identity
Additive inverse
Associative property
Scalar identity
D) This set is a vector space. All ten vector space axioms hold.
E) This set is not a vector space. It fails the following axioms.
Closer under addition
Closer under scalar multiplication

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
24
Determine whether the set of all third-degree polynomial functions as given below, whose graphs pass through the origin with the standard operations, is a vector space. If it is not, then determine the set of axioms that it fails. 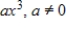
A) This set is not a vector space. It fails the following axioms.
Commutative property
Additive identity
Distributive property
B) This set is not a vector space. It fails the following axioms.
Scalar identity
Associative property
Distributive property
Additive identity
C) This set is not a vector space. It fails the following axioms.
Additive identity
Additive inverse
Associative property
Scalar identity
D) This set is a vector space. All ten vector space axioms hold.
E) This set is not a vector space. It fails the following axioms.
Closer under addition
Closer under scalar multiplication
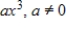
A) This set is not a vector space. It fails the following axioms.
Commutative property
Additive identity
Distributive property
B) This set is not a vector space. It fails the following axioms.
Scalar identity
Associative property
Distributive property
Additive identity
C) This set is not a vector space. It fails the following axioms.
Additive identity
Additive inverse
Associative property
Scalar identity
D) This set is a vector space. All ten vector space axioms hold.
E) This set is not a vector space. It fails the following axioms.
Closer under addition
Closer under scalar multiplication

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
25
Determine whether the set of all fourth-degree polynomial functions as given below, whose graphs pass through the origin with the standard operations, is a vector space. If it is not, then determine the set of axioms that it fails. 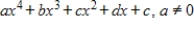
A) This set is not a vector space. It fails the following axioms.
Commutative property
Additive identity
Distributive property
B) This set is not a vector space. It fails the following axioms.
Scalar identity
Associative property
Distributive property
Additive identity
C) This set is not a vector space. It fails the following axioms.
Additive identity
Additive inverse
Associative property
Scalar identity
D) This set is a vector space. All ten vector space axioms hold.
E) This set is not a vector space. It fails the following axioms.
Closer under addition
Closer under scalar multiplication
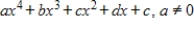
A) This set is not a vector space. It fails the following axioms.
Commutative property
Additive identity
Distributive property
B) This set is not a vector space. It fails the following axioms.
Scalar identity
Associative property
Distributive property
Additive identity
C) This set is not a vector space. It fails the following axioms.
Additive identity
Additive inverse
Associative property
Scalar identity
D) This set is a vector space. All ten vector space axioms hold.
E) This set is not a vector space. It fails the following axioms.
Closer under addition
Closer under scalar multiplication

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
26
Determine whether the following set with the standard operations, is a vector space. If it is not, then determine the set of axioms that it fails. 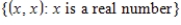
A) This set is a vector space. All ten vector space axioms hold.
B) This set is not a vector space. It fails the following axioms.
Scalar identity
Associative property
Distributive property
Additive identity
C) This set is not a vector space. It fails the following axioms.
Commutative property
Additive identity
Distributive property
D) This set is not a vector space. It fails the following axioms.
Additive identity
Additive inverse
Associative property
Scalar identity
E) This set is not a vector space. It fails the following axioms.
Closer under addition
Closer under scalar multiplication
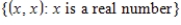
A) This set is a vector space. All ten vector space axioms hold.
B) This set is not a vector space. It fails the following axioms.
Scalar identity
Associative property
Distributive property
Additive identity
C) This set is not a vector space. It fails the following axioms.
Commutative property
Additive identity
Distributive property
D) This set is not a vector space. It fails the following axioms.
Additive identity
Additive inverse
Associative property
Scalar identity
E) This set is not a vector space. It fails the following axioms.
Closer under addition
Closer under scalar multiplication

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
27
Determine whether the following set with the standard operations, is a vector space. If it is not, then determine the set of axioms that it fails.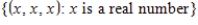
A) This set is a vector space. All ten vector space axioms hold.
B) This set is not a vector space. It fails the following axioms.
Scalar identity
Associative property
Distributive property
Additive identity
C) This set is not a vector space. It fails the following axioms.
Commutative property
Additive identity
Distributive property
D) This set is not a vector space. It fails the following axioms.
Additive identity
Additive inverse
Associative property
Scalar identity
E) This set is not a vector space. It fails the following axioms.
Closer under addition
Closer under scalar multiplication
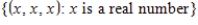
A) This set is a vector space. All ten vector space axioms hold.
B) This set is not a vector space. It fails the following axioms.
Scalar identity
Associative property
Distributive property
Additive identity
C) This set is not a vector space. It fails the following axioms.
Commutative property
Additive identity
Distributive property
D) This set is not a vector space. It fails the following axioms.
Additive identity
Additive inverse
Associative property
Scalar identity
E) This set is not a vector space. It fails the following axioms.
Closer under addition
Closer under scalar multiplication

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
28
Determine whether the following set with the standard operations, is a vector space. If it is not, then determine the set of axioms that it fails. 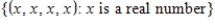
A) This set is a vector space. All ten vector space axioms hold.
B) This set is not a vector space. It fails the following axioms.
Scalar identity
Associative property
Distributive property
Additive identity
C) This set is not a vector space. It fails the following axioms.
Commutative property
Additive identity
Distributive property
D) This set is not a vector space. It fails the following axioms.
Additive identity
Additive inverse
Associative property
Scalar identity
E) This set is not a vector space. It fails the following axioms.
Closer under addition
Closer under scalar multiplication
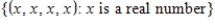
A) This set is a vector space. All ten vector space axioms hold.
B) This set is not a vector space. It fails the following axioms.
Scalar identity
Associative property
Distributive property
Additive identity
C) This set is not a vector space. It fails the following axioms.
Commutative property
Additive identity
Distributive property
D) This set is not a vector space. It fails the following axioms.
Additive identity
Additive inverse
Associative property
Scalar identity
E) This set is not a vector space. It fails the following axioms.
Closer under addition
Closer under scalar multiplication

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
29
Determine whether the following set with the standard operations, is a vector space. If it is not, then determine the set of axioms that it fails. 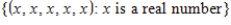
A) This set is a vector space. All ten vector space axioms hold.
B) This set is not a vector space. It fails the following axioms.
Scalar identity
Associative property
Distributive property
Additive identity
C) This set is not a vector space. It fails the following axioms.
Commutative property
Additive identity
Distributive property
D) This set is not a vector space. It fails the following axioms.
Additive identity
Additive inverse
Associative property
Scalar identity
E) This set is not a vector space. It fails the following axioms.
Closer under addition
Closer under scalar multiplication
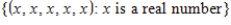
A) This set is a vector space. All ten vector space axioms hold.
B) This set is not a vector space. It fails the following axioms.
Scalar identity
Associative property
Distributive property
Additive identity
C) This set is not a vector space. It fails the following axioms.
Commutative property
Additive identity
Distributive property
D) This set is not a vector space. It fails the following axioms.
Additive identity
Additive inverse
Associative property
Scalar identity
E) This set is not a vector space. It fails the following axioms.
Closer under addition
Closer under scalar multiplication

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
30
Determine whether the set of all 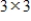 diagonal matrices with the standard operations, is a vector space. If it is not, then determine the set of axioms that it fails.
diagonal matrices with the standard operations, is a vector space. If it is not, then determine the set of axioms that it fails.
A) This set is not a vector space. It fails the following axioms.
Commutative property
Additive identity
Distributive property
B) This set is not a vector space. It fails the following axioms.
Scalar identity
Associative property
Distributive property
Additive identity
C) This set is not a vector space. It fails the following axioms.
Closer under addition
Closer under scalar multiplication
D) This set is not a vector space. It fails the following axioms.
Additive identity
Additive inverse
Associative property
Scalar identity
E) This set is a vector space. All ten vector space axioms hold.
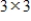 diagonal matrices with the standard operations, is a vector space. If it is not, then determine the set of axioms that it fails.
diagonal matrices with the standard operations, is a vector space. If it is not, then determine the set of axioms that it fails.A) This set is not a vector space. It fails the following axioms.
Commutative property
Additive identity
Distributive property
B) This set is not a vector space. It fails the following axioms.
Scalar identity
Associative property
Distributive property
Additive identity
C) This set is not a vector space. It fails the following axioms.
Closer under addition
Closer under scalar multiplication
D) This set is not a vector space. It fails the following axioms.
Additive identity
Additive inverse
Associative property
Scalar identity
E) This set is a vector space. All ten vector space axioms hold.

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
31
Verify 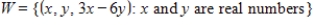 is a subspace of
is a subspace of 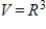 .
.
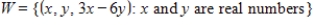 is a subspace of
is a subspace of 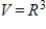 .
.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
32
W is the set of all functions that are differentiable on 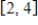 . V is the set of all functions that are continuous on
. V is the set of all functions that are continuous on 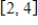 . Verify W is a subspace of V.
. Verify W is a subspace of V.
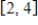 . V is the set of all functions that are continuous on
. V is the set of all functions that are continuous on 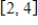 . Verify W is a subspace of V.
. Verify W is a subspace of V.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
33
the following subset of 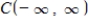 is a subspace of
is a subspace of 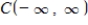 .The set of all nonnegative functions:
.The set of all nonnegative functions: 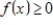
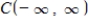 is a subspace of
is a subspace of 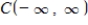 .The set of all nonnegative functions:
.The set of all nonnegative functions: 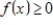

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
34
the following subset of 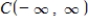 is a subspace of
is a subspace of 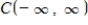 .The set of all nonpositive functions:
.The set of all nonpositive functions: 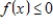
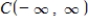 is a subspace of
is a subspace of 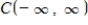 .The set of all nonpositive functions:
.The set of all nonpositive functions: 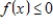

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
35
the following subset of 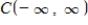 is a subspace of
is a subspace of 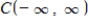 .The set of all positive functions:
.The set of all positive functions: 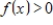
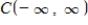 is a subspace of
is a subspace of 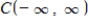 .The set of all positive functions:
.The set of all positive functions: 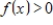

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
36
the following subset of 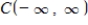 is a subspace of
is a subspace of 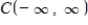 .The set of all negative functions:
.The set of all negative functions: 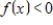
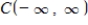 is a subspace of
is a subspace of 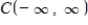 .The set of all negative functions:
.The set of all negative functions: 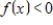

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
37
the following subset of 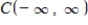 is a subspace of
is a subspace of 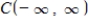 .The set of all zero functions:
.The set of all zero functions: 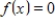
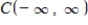 is a subspace of
is a subspace of 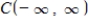 .The set of all zero functions:
.The set of all zero functions: 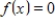

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
38
the following subset of 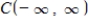 is a subspace of
is a subspace of 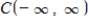 .The set of all constant functions:
.The set of all constant functions: 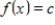
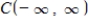 is a subspace of
is a subspace of 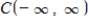 .The set of all constant functions:
.The set of all constant functions: 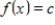

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
39
The set of all functions such that 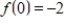 is a subspace of
is a subspace of 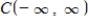 .
.
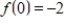 is a subspace of
is a subspace of 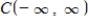 .
.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
40
The set of all 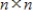 lower triangular matrices is a subspace of
lower triangular matrices is a subspace of 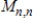 .
.
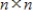 lower triangular matrices is a subspace of
lower triangular matrices is a subspace of 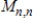 .
.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
41
The set of all 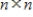 singular matrices is a subspace of
singular matrices is a subspace of 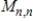 .
.
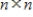 singular matrices is a subspace of
singular matrices is a subspace of 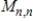 .
.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
42
? The set 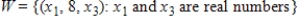 is a subspace of
is a subspace of 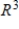 with the standard operations.
with the standard operations.
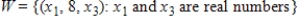 is a subspace of
is a subspace of 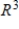 with the standard operations.
with the standard operations. 
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
43
The set 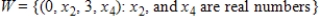 is a subspace of
is a subspace of 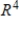 with the standard operations.
with the standard operations.
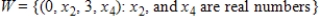 is a subspace of
is a subspace of 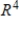 with the standard operations.
with the standard operations. 
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
44
The set 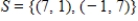 spans
spans 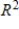 .
.
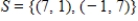 spans
spans  .
.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
45
The set 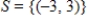 spans
spans 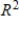 .
.
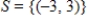 spans
spans 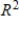 .
.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
46
The set 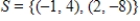 spans
spans 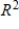 .
.
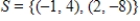 spans
spans 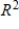 .
.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
47
The set 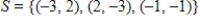 spans
spans 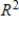 .
.
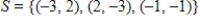 spans
spans 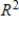 .
.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
48
The set 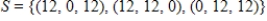 spans
spans 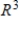 .
.
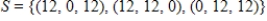 spans
spans 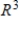 .
.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
49
The set 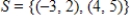 is linearly independent.
is linearly independent.
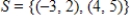 is linearly independent.
is linearly independent.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
50
The set 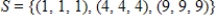 is linearly independent.
is linearly independent.
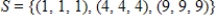 is linearly independent.
is linearly independent.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
51
The set 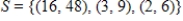 is linearly dependent. Express the first vector as a linear combination of the other two vectors.
is linearly dependent. Express the first vector as a linear combination of the other two vectors.
A)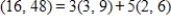
B)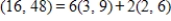
C)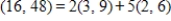
D)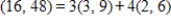
E)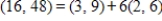
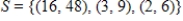 is linearly dependent. Express the first vector as a linear combination of the other two vectors.
is linearly dependent. Express the first vector as a linear combination of the other two vectors.A)
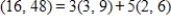
B)
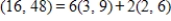
C)
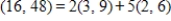
D)
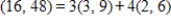
E)
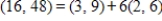

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
52
The set 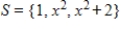 spans
spans 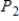 .
.
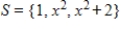 spans
spans 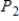 .
.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
53
Write the standard basis for the vector space 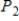 .
.
A)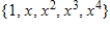
B)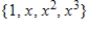
C)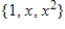
D)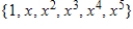
E)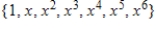
 .
.A)
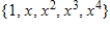
B)
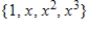
C)
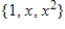
D)
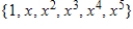
E)
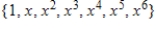

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
54
Write the standard basis for the vector space 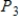 .
.
A)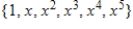
B)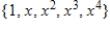
C)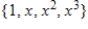
D)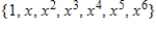
E)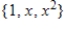
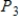 .
.A)
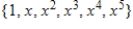
B)
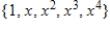
C)
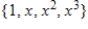
D)
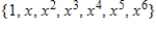
E)
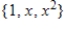

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
55
Write the standard basis for the vector space 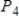 .
.
A)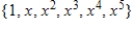
B)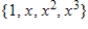
C)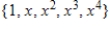
D)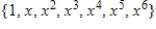
E)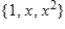
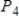 .
.A)
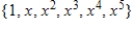
B)
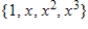
C)
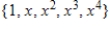
D)
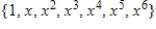
E)
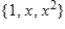

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
56
Write the standard basis for the vector space 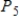 .
.
A)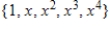
B)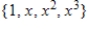
C)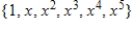
D)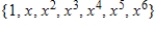
E)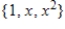
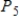 .
.A)
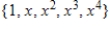
B)
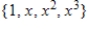
C)
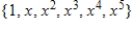
D)
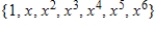
E)
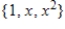

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
57
Write the standard basis for the vector space 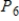 .
.
A)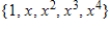
B)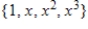
C)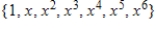
D)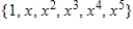
E)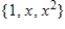
 .
.A)
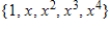
B)
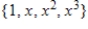
C)
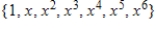
D)
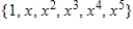
E)
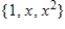

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
58
Explain why 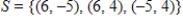 is not a basis for
is not a basis for 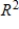 .
.
A) S is linearly independent and spans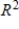
B) S is linearly dependent and does not span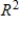
C) S is linearly independent and does not span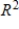
D) S is linearly dependent and spans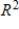
E) none of these choices
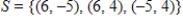 is not a basis for
is not a basis for 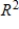 .
.A) S is linearly independent and spans
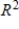
B) S is linearly dependent and does not span
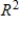
C) S is linearly independent and does not span
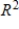
D) S is linearly dependent and spans
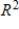
E) none of these choices

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
59
Explain why 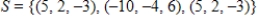 is not a basis for
is not a basis for 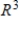 .
.
A) S is linearly independent and spans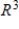
B) S is linearly dependent and spans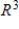
C) S is linearly independent and does not span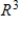
D) S is linearly dependent and does not span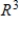
E) none of these choices
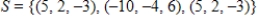 is not a basis for
is not a basis for 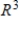 .
.A) S is linearly independent and spans
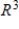
B) S is linearly dependent and spans
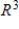
C) S is linearly independent and does not span
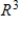
D) S is linearly dependent and does not span
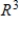
E) none of these choices

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
60
Explain why 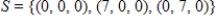 is not a basis for
is not a basis for 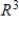 .
.
A) S is linearly independent and spans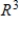
B) S is linearly dependent and spans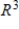
C) S is linearly dependent and does not span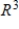
D) S is linearly independent and does not span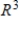
E) none of these choices
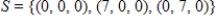 is not a basis for
is not a basis for 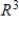 .
.A) S is linearly independent and spans
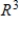
B) S is linearly dependent and spans
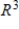
C) S is linearly dependent and does not span
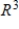
D) S is linearly independent and does not span
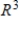
E) none of these choices

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
61
Explain why 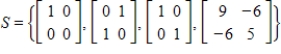 is not a basis for
is not a basis for 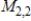 .
.
A) S is linearly dependent and does not span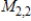
B) S is linearly dependent and spans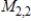
C) S is linearly independent and spans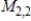
D) S is linearly independent and does not span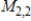
E) none of these choices
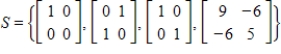 is not a basis for
is not a basis for 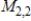 .
.A) S is linearly dependent and does not span
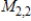
B) S is linearly dependent and spans
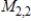
C) S is linearly independent and spans
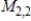
D) S is linearly independent and does not span
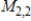
E) none of these choices

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
62
The set 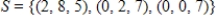 is a basis for
is a basis for 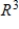 .
.
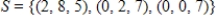 is a basis for
is a basis for 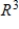 .
.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
63
The set 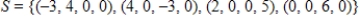 is a basis for
is a basis for 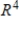 .
.
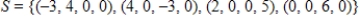 is a basis for
is a basis for 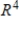 .
.
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
64
Determine whether 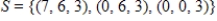 is a basis for
is a basis for 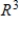 . If it is, write
. If it is, write 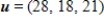 as a linear combination of the vectors in S.?
as a linear combination of the vectors in S.?
A) S is a basis for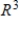 and
and 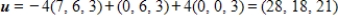
B) S is a basis for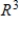 and
and 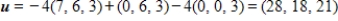
C) S is a basis for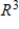 and
and 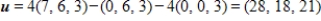
D) S is a basis for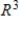 and
and 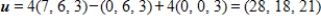
E) S is not a basis for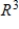
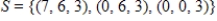 is a basis for
is a basis for 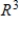 . If it is, write
. If it is, write 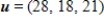 as a linear combination of the vectors in S.?
as a linear combination of the vectors in S.?A) S is a basis for
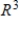 and
and 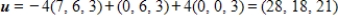
B) S is a basis for
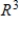 and
and 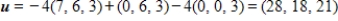
C) S is a basis for
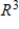 and
and 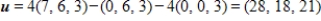
D) S is a basis for
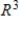 and
and 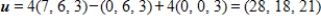
E) S is not a basis for
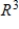

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
65
Determine whether 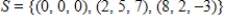 is a basis for
is a basis for 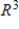 . If it is, write
. If it is, write 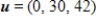 as a linear combination of the vectors in S.?
as a linear combination of the vectors in S.?
A) S is a basis for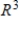 and
and 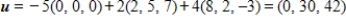
B) S is a basis for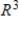 and ?
and ? 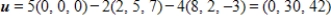
C) S is a basis for and
and 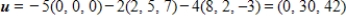
D) S is a basis for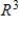 and
and 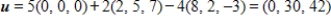
E) S is not a basis for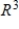
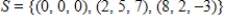 is a basis for
is a basis for 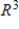 . If it is, write
. If it is, write 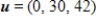 as a linear combination of the vectors in S.?
as a linear combination of the vectors in S.?A) S is a basis for
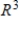 and
and 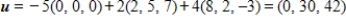
B) S is a basis for
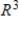 and ?
and ? 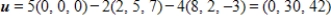
C) S is a basis for
 and
and 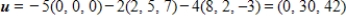
D) S is a basis for
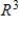 and
and 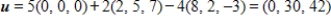
E) S is not a basis for
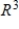

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
66
Determine whether 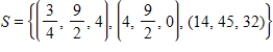 is a basis for
is a basis for 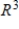 . If it is, write
. If it is, write 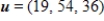 as a linear combination of the vectors in S.?
as a linear combination of the vectors in S.?
A) S is a basis for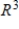 and
and 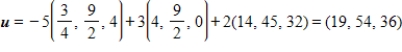
B) S is a basis for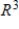 and
and 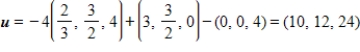
C) S is a basis for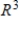 and
and 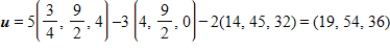
D) S is a basis for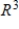 and
and 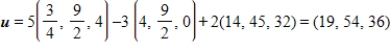
E) S is not a basis for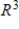
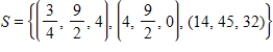 is a basis for
is a basis for 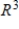 . If it is, write
. If it is, write 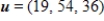 as a linear combination of the vectors in S.?
as a linear combination of the vectors in S.?A) S is a basis for
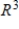 and
and 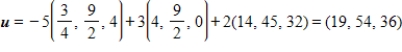
B) S is a basis for
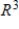 and
and 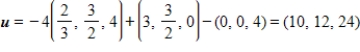
C) S is a basis for
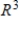 and
and 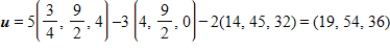
D) S is a basis for
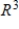 and
and 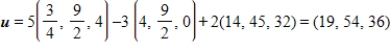
E) S is not a basis for

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
67
Find a basis for the column space of the matrix 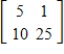 .
.
A)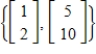
B)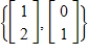
C)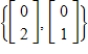
D)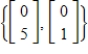
E)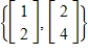
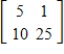 .
.A)
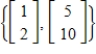
B)
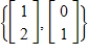
C)
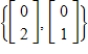
D)
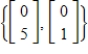
E)
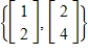

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
68
Find a basis for the row space of a matrix 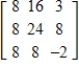 .
.
A)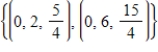
B)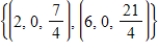
C)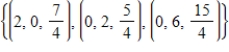
D)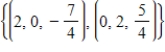
E)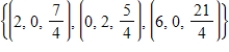
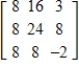 .
.A)
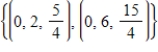
B)
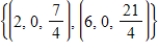
C)
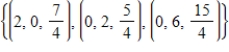
D)
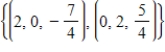
E)
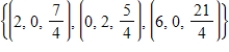

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
69
Find the rank of the matrix 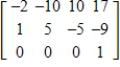
A) 2
B) 0
C) 4
D) 3
E) 1
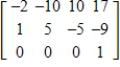
A) 2
B) 0
C) 4
D) 3
E) 1

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
70
Find a basis for the subspace of 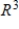 spanned by
spanned by 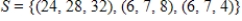 .
.
A)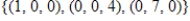
B)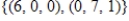
C)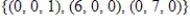
D)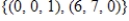
E)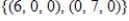
 spanned by
spanned by 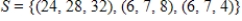 .
.A)
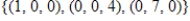
B)
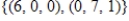
C)
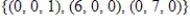
D)
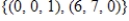
E)
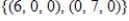

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
71
Find a basis for the subspace of 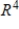 spanned by
spanned by 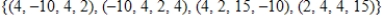 .
.
A)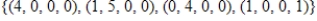
B)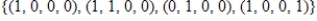
C)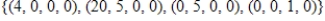
D)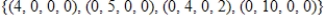
E)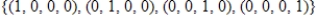
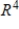 spanned by
spanned by 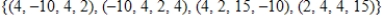 .
.A)
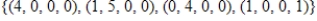
B)
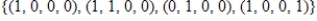
C)
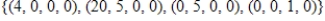
D)
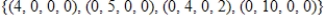
E)
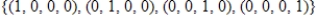

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
72
Find a basis for and the dimension of the solution space of 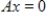 .
. 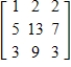
A)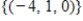 , dim = 1
, dim = 1
B)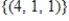 , dim = 3
, dim = 3
C)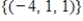 , dim = 1
, dim = 1
D)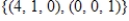 ? , dim = 2
? , dim = 2
E)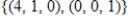 , dim = 3
, dim = 3
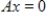 .
. 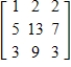
A)
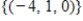 , dim = 1
, dim = 1B)
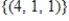 , dim = 3
, dim = 3C)
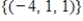 , dim = 1
, dim = 1D)
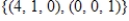 ? , dim = 2
? , dim = 2E)
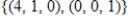 , dim = 3
, dim = 3
Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
73
Find a basis for the solution space of the following homogeneous system of linear equations. 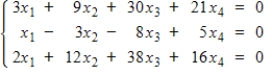
A)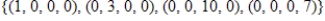
B)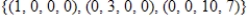
C)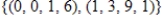
D)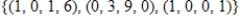
E)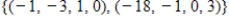
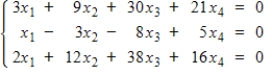
A)
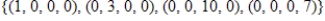
B)
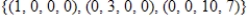
C)
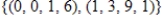
D)
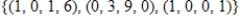
E)
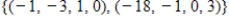

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
74
Determine whether B is in the column space of A. If it is, write B as a linear combination of the column vectors of A..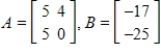
A)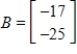 is in the column space of A and
is in the column space of A and 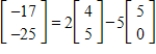
B)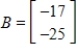 is in the column space of A and
is in the column space of A and 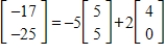
C)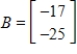 is in the column space of A and
is in the column space of A and 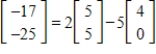
D)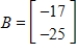 does not belong to the column space of
does not belong to the column space of 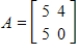
E) none of these choices
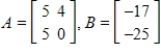
A)
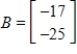 is in the column space of A and
is in the column space of A and 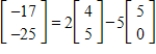
B)
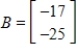 is in the column space of A and
is in the column space of A and 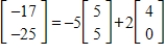
C)
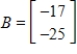 is in the column space of A and
is in the column space of A and 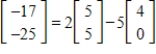
D)
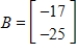 does not belong to the column space of
does not belong to the column space of 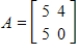
E) none of these choices

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
75
Given that 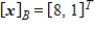 , the coordinate matrix of x relative to a (nonstandard) basis
, the coordinate matrix of x relative to a (nonstandard) basis 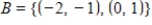 find the coordinate vector of x relative to the standard basis in
find the coordinate vector of x relative to the standard basis in 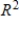 .
.
A)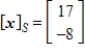
B)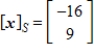
C)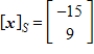
D)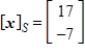
E)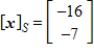
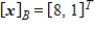 , the coordinate matrix of x relative to a (nonstandard) basis
, the coordinate matrix of x relative to a (nonstandard) basis 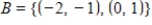 find the coordinate vector of x relative to the standard basis in
find the coordinate vector of x relative to the standard basis in  .
.A)
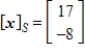
B)
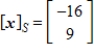
C)
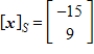
D)
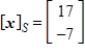
E)
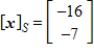

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
76
Given that 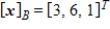 , the coordinate matrix of x relative to a (nonstandard) basis
, the coordinate matrix of x relative to a (nonstandard) basis 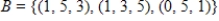 . Find the coordinate vector of x relative to the standard basis in
. Find the coordinate vector of x relative to the standard basis in 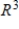 .
.
A)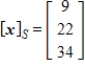
B)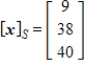
C)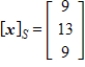
D)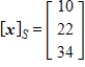
E)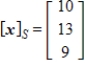
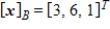 , the coordinate matrix of x relative to a (nonstandard) basis
, the coordinate matrix of x relative to a (nonstandard) basis 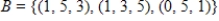 . Find the coordinate vector of x relative to the standard basis in
. Find the coordinate vector of x relative to the standard basis in 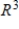 .
.A)
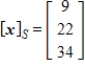
B)
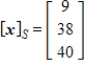
C)
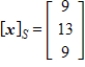
D)
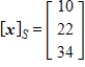
E)
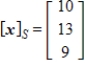

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
77
Given that 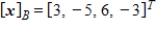 , the coordinate matrix of x relative to a (nonstandard) basis
, the coordinate matrix of x relative to a (nonstandard) basis 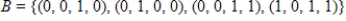 . Find the coordinate vector of x relative to the standard basis in
. Find the coordinate vector of x relative to the standard basis in 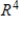 .
.
A)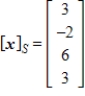
B)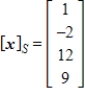
C)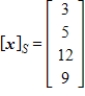
D)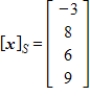
E)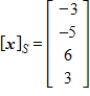
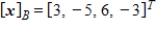 , the coordinate matrix of x relative to a (nonstandard) basis
, the coordinate matrix of x relative to a (nonstandard) basis 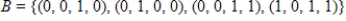 . Find the coordinate vector of x relative to the standard basis in
. Find the coordinate vector of x relative to the standard basis in 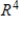 .
.A)
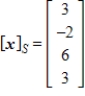
B)
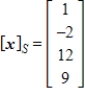
C)
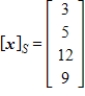
D)
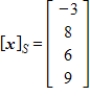
E)
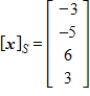

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
78
Find the transition matrix from 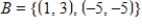 to
to 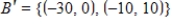 .
.
A)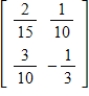
B)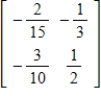
C)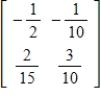
D)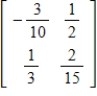
E)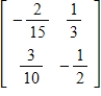
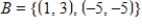 to
to 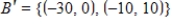 .
.A)

B)
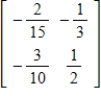
C)
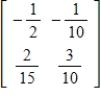
D)

E)
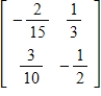

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
79
Find the coordinate matrix of 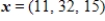 in
in 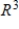 relative to the basis
relative to the basis 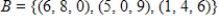 .
.
A)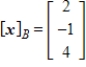
B)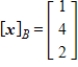
C)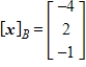
D)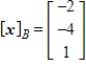
E)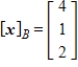
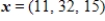 in
in 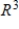 relative to the basis
relative to the basis 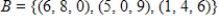 .
.A)
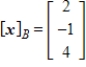
B)
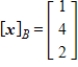
C)
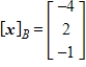
D)
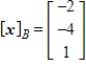
E)
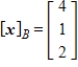

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck
80
Find the transition matrix from 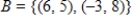 to
to 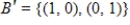 by hand.
by hand.
A)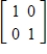
B)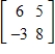
C)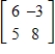
D)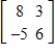
E)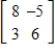
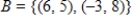 to
to 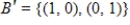 by hand.
by hand.A)
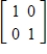
B)
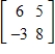
C)
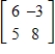
D)
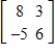
E)
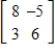

Unlock Deck
Unlock for access to all 100 flashcards in this deck.
Unlock Deck
k this deck


