Exam 4: Vector Spaces
Exam 1: Linear Equations25 Questions
Exam 2: Matrices48 Questions
Exam 3: Determinants47 Questions
Exam 4: Vector Spaces100 Questions
Exam 5: Inner Product Spaces54 Questions
Exam 6: Linear Transformations46 Questions
Exam 7: Eigenvalues Eigenvectors32 Questions
Select questions type
Describe the zero vector (the additive identity) of the vector space 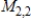 .
.
Free
(Multiple Choice)
4.9/5  (33)
(33)
Correct Answer:
B
Find a basis for the subspace of 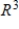 spanned by
spanned by 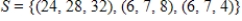 .
.
Free
(Multiple Choice)
4.7/5  (34)
(34)
Correct Answer:
D
Determine whether 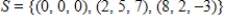 is a basis for
is a basis for 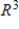 . If it is, write
. If it is, write 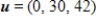 as a linear combination of the vectors in S.?
as a linear combination of the vectors in S.?
Free
(Multiple Choice)
4.9/5  (34)
(34)
Correct Answer:
E
Describe the zero vector (the additive identity) of the vector space 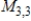 .
.
(Multiple Choice)
4.8/5  (31)
(31)
Find the coordinate matrix of 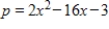 relative to the standard basis in
relative to the standard basis in 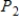 .
.
(Multiple Choice)
4.8/5  (41)
(41)
Find a basis for and the dimension of the solution space of 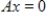 .
. 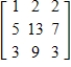
(Multiple Choice)
4.9/5  (43)
(43)
Perform a rotation of axes to eliminate the xy-term, and sketch the graph of the conic defined by the function below. 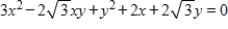
(Multiple Choice)
4.7/5  (36)
(36)
the following subset of 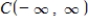 is a subspace of
is a subspace of 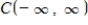 .The set of all nonpositive functions:
.The set of all nonpositive functions: 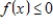
(True/False)
4.9/5  (39)
(39)
Given that 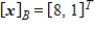 , the coordinate matrix of x relative to a (nonstandard) basis
, the coordinate matrix of x relative to a (nonstandard) basis 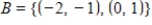 find the coordinate vector of x relative to the standard basis in
find the coordinate vector of x relative to the standard basis in 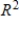 .
.
(Multiple Choice)
4.8/5  (30)
(30)
Determine whether the set of all third-degree polynomial functions as given below, whose graphs pass through the origin with the standard operations, is a vector space. If it is not, then determine the set of axioms that it fails. 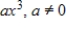
(Multiple Choice)
4.7/5  (36)
(36)
Determine whether 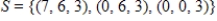 is a basis for
is a basis for 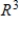 . If it is, write
. If it is, write 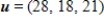 as a linear combination of the vectors in S.?
as a linear combination of the vectors in S.?
(Multiple Choice)
4.7/5  (31)
(31)
Determine whether the set of all first-degree polynomial functions as given below, whose graphs pass through the origin with the standard operations, is a vector space. If it is not, then determine the set of axioms that it fails. 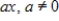
(Multiple Choice)
4.8/5  (28)
(28)
Given that 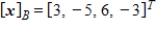 , the coordinate matrix of x relative to a (nonstandard) basis
, the coordinate matrix of x relative to a (nonstandard) basis 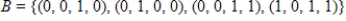 . Find the coordinate vector of x relative to the standard basis in
. Find the coordinate vector of x relative to the standard basis in 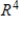 .
.
(Multiple Choice)
4.7/5  (36)
(36)
Showing 1 - 20 of 100
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)