Deck 18: Differential Forms and Exterior Calculus
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/76
Play
Full screen (f)
Deck 18: Differential Forms and Exterior Calculus
1
Let 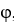 ,
, 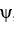 ,
, 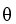 be 1-forms and
be 1-forms and 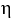 be a 2-form on
be a 2-form on 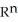 . Which of the following is a 3-form on
. Which of the following is a 3-form on 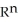 ?
?
A) 11ee7971_d7c9_b5d4_88d3_75d03a1ac3e7_TB9661_11 + 11ee7972_1f9d_0245_88d3_430fabc730ac_TB9661_11 + 11ee7972_a99a_a1a7_88d3_5bac39f31ff0_TB9661_11
B) 11ee7971_d7c9_b5d4_88d3_75d03a1ac3e7_TB9661_11 + 11ee7972_e728_fe48_88d3_fd489bade70a_TB9661_11
C) (11ee7971_d7c9_b5d4_88d3_75d03a1ac3e7_TB9661_11 +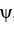 )
)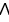 11ee7972_a99a_a1a7_88d3_5bac39f31ff0_TB9661_11
11ee7972_a99a_a1a7_88d3_5bac39f31ff0_TB9661_11
D)11ee7971_d7c9_b5d4_88d3_75d03a1ac3e7_TB9661_11 11ee7973_0b66_7d59_88d3_6bcf237f8512_TB9661_11 11ee7972_5038_6616_88d3_2d4d40837c09_TB9661_11 11ee7973_0b66_7d59_88d3_6bcf237f8512_TB9661_11 11ee7972_a99a_a1a7_88d3_5bac39f31ff0_TB9661_11
E) All of the above
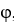 ,
, 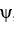 ,
, 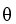 be 1-forms and
be 1-forms and 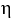 be a 2-form on
be a 2-form on 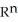 . Which of the following is a 3-form on
. Which of the following is a 3-form on 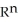 ?
?A) 11ee7971_d7c9_b5d4_88d3_75d03a1ac3e7_TB9661_11 + 11ee7972_1f9d_0245_88d3_430fabc730ac_TB9661_11 + 11ee7972_a99a_a1a7_88d3_5bac39f31ff0_TB9661_11
B) 11ee7971_d7c9_b5d4_88d3_75d03a1ac3e7_TB9661_11 + 11ee7972_e728_fe48_88d3_fd489bade70a_TB9661_11
C) (11ee7971_d7c9_b5d4_88d3_75d03a1ac3e7_TB9661_11 +
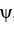 )
)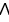 11ee7972_a99a_a1a7_88d3_5bac39f31ff0_TB9661_11
11ee7972_a99a_a1a7_88d3_5bac39f31ff0_TB9661_11 D)11ee7971_d7c9_b5d4_88d3_75d03a1ac3e7_TB9661_11 11ee7973_0b66_7d59_88d3_6bcf237f8512_TB9661_11 11ee7972_5038_6616_88d3_2d4d40837c09_TB9661_11 11ee7973_0b66_7d59_88d3_6bcf237f8512_TB9661_11 11ee7972_a99a_a1a7_88d3_5bac39f31ff0_TB9661_11
E) All of the above
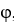
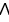
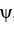 11ee7973_0b66_7d59_88d3_6bcf237f8512_TB9661_11
11ee7973_0b66_7d59_88d3_6bcf237f8512_TB9661_11 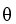
2
Let 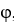 ,
, 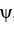 be differential 1-forms and let
be differential 1-forms and let 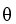 be a differential 0-form on
be a differential 0-form on 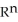 a domain D in Which of the following is a differential 2-form on D?
a domain D in Which of the following is a differential 2-form on D?
A) 11ee7971_d7c9_b5d4_88d3_75d03a1ac3e7_TB9661_11+ 11ee7972_5038_6616_88d3_2d4d40837c09_TB9661_11
B)11ee7971_d7c9_b5d4_88d3_75d03a1ac3e7_TB9661_11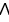 11ee7972_5038_6616_88d3_2d4d40837c09_TB9661_11
11ee7972_5038_6616_88d3_2d4d40837c09_TB9661_11
C) 311ee7971_d7c9_b5d4_88d3_75d03a1ac3e7_TB9661_11 - 11ee7972_5038_6616_88d3_2d4d40837c09_TB9661_11
D) + 11ee7972_5038_6616_88d3_2d4d40837c09_TB9661_11
+ 11ee7972_5038_6616_88d3_2d4d40837c09_TB9661_11
E) None of the above
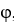 ,
, 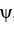 be differential 1-forms and let
be differential 1-forms and let 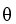 be a differential 0-form on
be a differential 0-form on 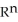 a domain D in Which of the following is a differential 2-form on D?
a domain D in Which of the following is a differential 2-form on D?A) 11ee7971_d7c9_b5d4_88d3_75d03a1ac3e7_TB9661_11+ 11ee7972_5038_6616_88d3_2d4d40837c09_TB9661_11
B)11ee7971_d7c9_b5d4_88d3_75d03a1ac3e7_TB9661_11
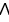 11ee7972_5038_6616_88d3_2d4d40837c09_TB9661_11
11ee7972_5038_6616_88d3_2d4d40837c09_TB9661_11C) 311ee7971_d7c9_b5d4_88d3_75d03a1ac3e7_TB9661_11 - 11ee7972_5038_6616_88d3_2d4d40837c09_TB9661_11
D)
 + 11ee7972_5038_6616_88d3_2d4d40837c09_TB9661_11
+ 11ee7972_5038_6616_88d3_2d4d40837c09_TB9661_11E) None of the above
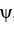
3
Find the dimension of 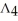 (
( 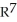 ).
).
A) 7
B) 840
C) 4
D) 3
E) 35
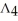 (
( 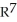 ).
).A) 7
B) 840
C) 4
D) 3
E) 35
35
4
Let k and n be integers such that 1 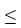 k 11ee7973_99f4_ef7a_88d3_478f26d4adc3_TB9661_11 n. Find the dimension of the vector space of all k-forms on
k 11ee7973_99f4_ef7a_88d3_478f26d4adc3_TB9661_11 n. Find the dimension of the vector space of all k-forms on 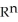 .
.
A)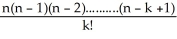
B) n
C) k
D) n - k
E) n(n - 1)(n - 2).....(n - k +1)
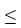 k 11ee7973_99f4_ef7a_88d3_478f26d4adc3_TB9661_11 n. Find the dimension of the vector space of all k-forms on
k 11ee7973_99f4_ef7a_88d3_478f26d4adc3_TB9661_11 n. Find the dimension of the vector space of all k-forms on 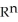 .
.A)
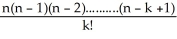
B) n
C) k
D) n - k
E) n(n - 1)(n - 2).....(n - k +1)

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
5
Let 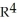 =
= 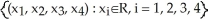 . List all basis vectors of
. List all basis vectors of 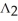 (
( 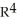 ).
).
A)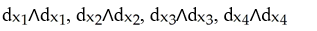
B)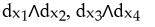
C)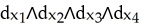
D)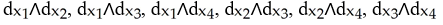
E)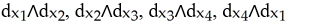
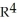 =
= 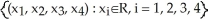 . List all basis vectors of
. List all basis vectors of 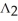 (
( 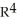 ).
).A)
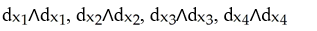
B)
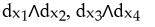
C)
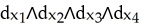
D)
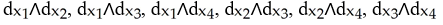
E)
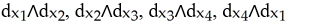

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
6
If 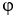 is a k-form and
is a k-form and 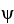 is an l-form on
is an l-form on 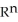 , then
, then 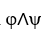 =
= 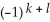 https://storage.examlex.com/TB9661/
https://storage.examlex.com/TB9661/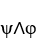 .
.
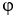 is a k-form and
is a k-form and 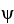 is an l-form on
is an l-form on  , then
, then 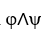 =
=  https://storage.examlex.com/TB9661/
https://storage.examlex.com/TB9661/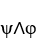 .
.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
7
Let φ and ψ be two 1-forms on 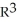 say φ=
say φ= 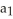 d
d 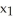 +
+ 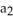 d
d 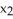 , ψ=
, ψ= 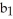 d
d 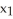 +
+ 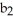 d
d 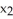 . Show that φ∧ψ = 0 if and only if φ = c ψ for some constant real number c.
. Show that φ∧ψ = 0 if and only if φ = c ψ for some constant real number c.
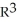 say φ=
say φ= 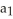 d
d 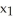 +
+ 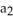 d
d 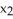 , ψ=
, ψ= 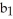 d
d 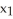 +
+ 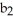 d
d 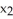 . Show that φ∧ψ = 0 if and only if φ = c ψ for some constant real number c.
. Show that φ∧ψ = 0 if and only if φ = c ψ for some constant real number c.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
8
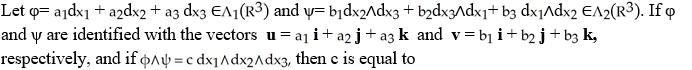
A) u . v
B) u × v
C) u + v
D)
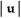 +
+ 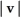
E)
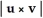

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
9
If 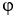 is a k -form,
is a k -form, 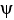 and
and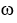 are l-forms on
are l-forms on 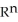 , then
, then 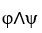 =
= 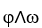 implies
implies 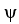 =https://storage.examlex.com/TB9661/
=https://storage.examlex.com/TB9661/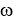 .
.
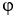 is a k -form,
is a k -form, 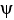 and
and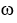 are l-forms on
are l-forms on 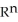 , then
, then 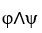 =
=  implies
implies  =https://storage.examlex.com/TB9661/
=https://storage.examlex.com/TB9661/ .
.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
10
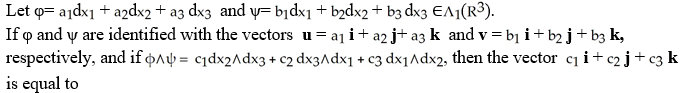
A) u + v
B) u - v
C) u × v
D) v × u
E) v - u

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
11
Let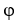 = 9dx - 2dy and
= 9dx - 2dy and 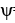 = -dx+ 3dy be 1 -forms on
= -dx+ 3dy be 1 -forms on 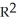 . Find all 1-forms
. Find all 1-forms  on
on 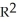 such that
such that 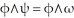 .
.
A) 11ee7975_2bfd_ecfa_88d3_cb60d904737e_TB9661_11 = t dx + (25 - 2t) dy, t
(25 - 2t) dy, t 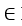 R
R
B) 11ee7975_2bfd_ecfa_88d3_cb60d904737e_TB9661_11 = t dx + (29 - 2t) dy, -
(29 - 2t) dy, - < t < 11ee7975_081b_3819_88d3_837de92b3d96_TB9661_11
< t < 11ee7975_081b_3819_88d3_837de92b3d96_TB9661_11
C) 11ee7975_2bfd_ecfa_88d3_cb60d904737e_TB9661_11 = t dx + (29 + 2t) dy, -11ee7975_081b_3819_88d3_837de92b3d96_TB9661_11 < t < 11ee7975_081b_3819_88d3_837de92b3d96_TB9661_11
(29 + 2t) dy, -11ee7975_081b_3819_88d3_837de92b3d96_TB9661_11 < t < 11ee7975_081b_3819_88d3_837de92b3d96_TB9661_11
D) 11ee7975_2bfd_ecfa_88d3_cb60d904737e_TB9661_11 = (25 + 9t) dx + t dy, t 11ee7974_eec1_32c8_88d3_178ace6e171f_TB9661_11 R
(25 + 9t) dx + t dy, t 11ee7974_eec1_32c8_88d3_178ace6e171f_TB9661_11 R
E) 11ee7975_2bfd_ecfa_88d3_cb60d904737e_TB9661_11 = (29 - 9t) dx + t dy, -11ee7975_081b_3819_88d3_837de92b3d96_TB9661_11 < t < 11ee7975_081b_3819_88d3_837de92b3d96_TB9661_11
(29 - 9t) dx + t dy, -11ee7975_081b_3819_88d3_837de92b3d96_TB9661_11 < t < 11ee7975_081b_3819_88d3_837de92b3d96_TB9661_11
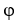 = 9dx - 2dy and
= 9dx - 2dy and 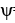 = -dx+ 3dy be 1 -forms on
= -dx+ 3dy be 1 -forms on  . Find all 1-forms
. Find all 1-forms  on
on 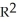 such that
such that 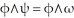 .
.A) 11ee7975_2bfd_ecfa_88d3_cb60d904737e_TB9661_11 = t dx +
 (25 - 2t) dy, t
(25 - 2t) dy, t 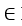 R
RB) 11ee7975_2bfd_ecfa_88d3_cb60d904737e_TB9661_11 = t dx +
 (29 - 2t) dy, -
(29 - 2t) dy, -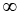 < t < 11ee7975_081b_3819_88d3_837de92b3d96_TB9661_11
< t < 11ee7975_081b_3819_88d3_837de92b3d96_TB9661_11C) 11ee7975_2bfd_ecfa_88d3_cb60d904737e_TB9661_11 = t dx +
 (29 + 2t) dy, -11ee7975_081b_3819_88d3_837de92b3d96_TB9661_11 < t < 11ee7975_081b_3819_88d3_837de92b3d96_TB9661_11
(29 + 2t) dy, -11ee7975_081b_3819_88d3_837de92b3d96_TB9661_11 < t < 11ee7975_081b_3819_88d3_837de92b3d96_TB9661_11D) 11ee7975_2bfd_ecfa_88d3_cb60d904737e_TB9661_11 =
 (25 + 9t) dx + t dy, t 11ee7974_eec1_32c8_88d3_178ace6e171f_TB9661_11 R
(25 + 9t) dx + t dy, t 11ee7974_eec1_32c8_88d3_178ace6e171f_TB9661_11 RE) 11ee7975_2bfd_ecfa_88d3_cb60d904737e_TB9661_11 =
 (29 - 9t) dx + t dy, -11ee7975_081b_3819_88d3_837de92b3d96_TB9661_11 < t < 11ee7975_081b_3819_88d3_837de92b3d96_TB9661_11
(29 - 9t) dx + t dy, -11ee7975_081b_3819_88d3_837de92b3d96_TB9661_11 < t < 11ee7975_081b_3819_88d3_837de92b3d96_TB9661_11
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
12
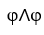 = 0 for every k-form
= 0 for every k-form 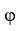 on
on 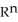 .
.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
13
Simplify a dx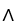 dy 11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11 dz + b dx
dy 11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11 dz + b dx dy + c dy11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11dz11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11dx + (a + b +c) dy
dy + c dy11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11dz11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11dx + (a + b +c) dy dy.
dy.
A) (a - b + c) dx dz
dz
B) (a +b + c) dx11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11dy11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11dz
C) (a - b - c) dx11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11dy11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11dz
D) (a + b -c) dx11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11dy11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11dz
E) (a + b +c) dx11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11dz11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11dy
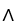 dy 11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11 dz + b dx
dy 11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11 dz + b dx dy + c dy11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11dz11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11dx + (a + b +c) dy
dy + c dy11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11dz11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11dx + (a + b +c) dy dy.
dy.A) (a - b + c) dx
 dz
dzB) (a +b + c) dx11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11dy11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11dz
C) (a - b - c) dx11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11dy11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11dz
D) (a + b -c) dx11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11dy11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11dz
E) (a + b +c) dx11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11dz11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11dy

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
14
Let 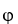 = 2dx + 5dy,
= 2dx + 5dy, 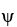 = -dx + 7dy and = -3dx + c dy be 1-forms on
= -dx + 7dy and = -3dx + c dy be 1-forms on 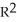 . Find the real number c such that 11ee7bbb_18dc_373c_ae82_e55d2b6d55c1_TB9661_11
. Find the real number c such that 11ee7bbb_18dc_373c_ae82_e55d2b6d55c1_TB9661_11 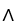 11ee7bbb_3770_208d_ae82_59bc8eff822f_TB9661_11 = 11ee7bbb_18dc_373c_ae82_e55d2b6d55c1_TB9661_11 11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11 .
11ee7bbb_3770_208d_ae82_59bc8eff822f_TB9661_11 = 11ee7bbb_18dc_373c_ae82_e55d2b6d55c1_TB9661_11 11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11 .
A) 12
B) 2
C) 17
D) -3
E) 0
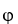 = 2dx + 5dy,
= 2dx + 5dy, 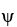 = -dx + 7dy and = -3dx + c dy be 1-forms on
= -dx + 7dy and = -3dx + c dy be 1-forms on  . Find the real number c such that 11ee7bbb_18dc_373c_ae82_e55d2b6d55c1_TB9661_11
. Find the real number c such that 11ee7bbb_18dc_373c_ae82_e55d2b6d55c1_TB9661_11 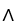 11ee7bbb_3770_208d_ae82_59bc8eff822f_TB9661_11 = 11ee7bbb_18dc_373c_ae82_e55d2b6d55c1_TB9661_11 11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11 .
11ee7bbb_3770_208d_ae82_59bc8eff822f_TB9661_11 = 11ee7bbb_18dc_373c_ae82_e55d2b6d55c1_TB9661_11 11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11 .A) 12
B) 2
C) 17
D) -3
E) 0

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
15
Let 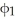 ,
, 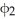 ,
, 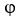 be m-forms,
be m-forms, 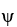 be a k-form, and
be a k-form, and 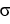 be an l-form on
be an l-form on 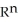 . Which of the following properties of the wedge product is not always true?
. Which of the following properties of the wedge product is not always true?
A) ( +
+ 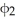 )
)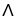 11ee7bbb_54a1_6c9e_ae82_5397d9492c20_TB9661_11 =
11ee7bbb_54a1_6c9e_ae82_5397d9492c20_TB9661_11 = 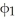 11ee7bbb_c9fe_971f_ae82_3b4fcccd2417_TB9661_11 11ee7bbb_54a1_6c9e_ae82_5397d9492c20_TB9661_11 +
11ee7bbb_c9fe_971f_ae82_3b4fcccd2417_TB9661_11 11ee7bbb_54a1_6c9e_ae82_5397d9492c20_TB9661_11 + 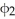 11ee7bbb_c9fe_971f_ae82_3b4fcccd2417_TB9661_11 11ee7bbb_54a1_6c9e_ae82_5397d9492c20_TB9661_11
11ee7bbb_c9fe_971f_ae82_3b4fcccd2417_TB9661_11 11ee7bbb_54a1_6c9e_ae82_5397d9492c20_TB9661_11
B) (11ee7bbc_2f42_a9a0_ae82_03df16557ec6_TB9661_11 11ee7bbb_c9fe_971f_ae82_3b4fcccd2417_TB9661_11 11ee7bbb_54a1_6c9e_ae82_5397d9492c20_TB9661_11 )11ee7bbb_c9fe_971f_ae82_3b4fcccd2417_TB9661_11 11ee7bbc_854e_b551_ae82_a1ccb48ff30b_TB9661_11 = 11ee7bbc_2f42_a9a0_ae82_03df16557ec6_TB9661_11 ( 11ee7bbc_854e_b551_ae82_a1ccb48ff30b_TB9661_11 )
11ee7bbc_854e_b551_ae82_a1ccb48ff30b_TB9661_11 )
C) 11ee7bbc_2f42_a9a0_ae82_03df16557ec6_TB9661_11 11ee7bbb_c9fe_971f_ae82_3b4fcccd2417_TB9661_11 11ee7bbb_54a1_6c9e_ae82_5397d9492c20_TB9661_11 = - 11ee7bbb_54a1_6c9e_ae82_5397d9492c20_TB9661_11 11ee7bbb_c9fe_971f_ae82_3b4fcccd2417_TB9661_11 11ee7bbc_2f42_a9a0_ae82_03df16557ec6_TB9661_11
D) (a 11ee7bbc_2f42_a9a0_ae82_03df16557ec6_TB9661_11 )11ee7bbb_c9fe_971f_ae82_3b4fcccd2417_TB9661_11 11ee7bbb_54a1_6c9e_ae82_5397d9492c20_TB9661_11 = a ( 11ee7bbb_54a1_6c9e_ae82_5397d9492c20_TB9661_11 ) for a
11ee7bbb_54a1_6c9e_ae82_5397d9492c20_TB9661_11 ) for a  R
R
E) for every k 1, there exists a zero k-form such that 11ee7bbb_54a1_6c9e_ae82_5397d9492c20_TB9661_11 + 0 = 11ee7bbb_54a1_6c9e_ae82_5397d9492c20_TB9661_11, and 0 11ee7bbb_c9fe_971f_ae82_3b4fcccd2417_TB9661_11 11ee7bbc_854e_b551_ae82_a1ccb48ff30b_TB9661_11 = 0.
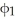 ,
, 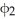 ,
, 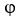 be m-forms,
be m-forms, 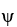 be a k-form, and
be a k-form, and 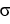 be an l-form on
be an l-form on  . Which of the following properties of the wedge product is not always true?
. Which of the following properties of the wedge product is not always true?A) (
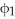 +
+ 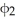 )
) 11ee7bbb_54a1_6c9e_ae82_5397d9492c20_TB9661_11 =
11ee7bbb_54a1_6c9e_ae82_5397d9492c20_TB9661_11 = 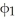 11ee7bbb_c9fe_971f_ae82_3b4fcccd2417_TB9661_11 11ee7bbb_54a1_6c9e_ae82_5397d9492c20_TB9661_11 +
11ee7bbb_c9fe_971f_ae82_3b4fcccd2417_TB9661_11 11ee7bbb_54a1_6c9e_ae82_5397d9492c20_TB9661_11 + 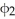 11ee7bbb_c9fe_971f_ae82_3b4fcccd2417_TB9661_11 11ee7bbb_54a1_6c9e_ae82_5397d9492c20_TB9661_11
11ee7bbb_c9fe_971f_ae82_3b4fcccd2417_TB9661_11 11ee7bbb_54a1_6c9e_ae82_5397d9492c20_TB9661_11B) (11ee7bbc_2f42_a9a0_ae82_03df16557ec6_TB9661_11 11ee7bbb_c9fe_971f_ae82_3b4fcccd2417_TB9661_11 11ee7bbb_54a1_6c9e_ae82_5397d9492c20_TB9661_11 )11ee7bbb_c9fe_971f_ae82_3b4fcccd2417_TB9661_11 11ee7bbc_854e_b551_ae82_a1ccb48ff30b_TB9661_11 = 11ee7bbc_2f42_a9a0_ae82_03df16557ec6_TB9661_11 (
 11ee7bbc_854e_b551_ae82_a1ccb48ff30b_TB9661_11 )
11ee7bbc_854e_b551_ae82_a1ccb48ff30b_TB9661_11 )C) 11ee7bbc_2f42_a9a0_ae82_03df16557ec6_TB9661_11 11ee7bbb_c9fe_971f_ae82_3b4fcccd2417_TB9661_11 11ee7bbb_54a1_6c9e_ae82_5397d9492c20_TB9661_11 = - 11ee7bbb_54a1_6c9e_ae82_5397d9492c20_TB9661_11 11ee7bbb_c9fe_971f_ae82_3b4fcccd2417_TB9661_11 11ee7bbc_2f42_a9a0_ae82_03df16557ec6_TB9661_11
D) (a 11ee7bbc_2f42_a9a0_ae82_03df16557ec6_TB9661_11 )11ee7bbb_c9fe_971f_ae82_3b4fcccd2417_TB9661_11 11ee7bbb_54a1_6c9e_ae82_5397d9492c20_TB9661_11 = a (
 11ee7bbb_54a1_6c9e_ae82_5397d9492c20_TB9661_11 ) for a
11ee7bbb_54a1_6c9e_ae82_5397d9492c20_TB9661_11 ) for a  R
RE) for every k 1, there exists a zero k-form such that 11ee7bbb_54a1_6c9e_ae82_5397d9492c20_TB9661_11 + 0 = 11ee7bbb_54a1_6c9e_ae82_5397d9492c20_TB9661_11, and 0 11ee7bbb_c9fe_971f_ae82_3b4fcccd2417_TB9661_11 11ee7bbc_854e_b551_ae82_a1ccb48ff30b_TB9661_11 = 0.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
16
Let ei , i = 1, 2, 3, 4 be the standard basis vectors in R4 and let 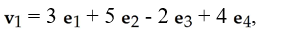
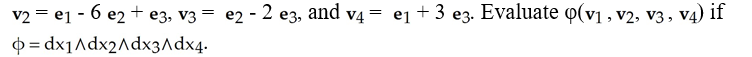
A) 32
B) -56
C) -40
D) -14
E) 40
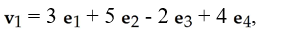
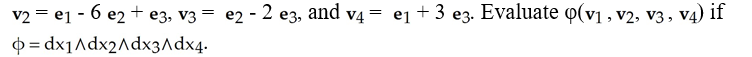
A) 32
B) -56
C) -40
D) -14
E) 40

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
17
Let ψ = 12dy∧dz -10 dx∧dz + 8 dx∧dy be a 2-form on  . Express ψ as a product of two 1-forms.Hint: Add a suitable multiple of dz∧dz = 0 to ψ.
. Express ψ as a product of two 1-forms.Hint: Add a suitable multiple of dz∧dz = 0 to ψ.
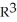 . Express ψ as a product of two 1-forms.Hint: Add a suitable multiple of dz∧dz = 0 to ψ.
. Express ψ as a product of two 1-forms.Hint: Add a suitable multiple of dz∧dz = 0 to ψ.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
18
Let σ = d 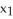 ∧d
∧d 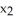 + d
+ d 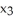 ∧d
∧d 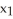 be a 2-form on
be a 2-form on 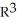 . Express σ as a product of two 1-forms.
. Express σ as a product of two 1-forms.
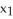 ∧d
∧d 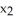 + d
+ d 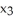 ∧d
∧d 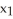 be a 2-form on
be a 2-form on 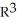 . Express σ as a product of two 1-forms.
. Express σ as a product of two 1-forms.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
19
Show that if φ is a k-form on 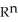 , then φ∧φ = 0 if k is odd.
, then φ∧φ = 0 if k is odd.
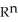 , then φ∧φ = 0 if k is odd.
, then φ∧φ = 0 if k is odd.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
20
Let ![Let be the permutation that maps [1, 2, 3, 4, 5] to [3, 4, 5, 2, 1], then sgn( ) = -1.](https://storage.examlex.com/TB9661/11ee7bbc_f5df_3c93_ae82_ade676104027_TB9661_11.jpg) be the permutation that maps [1, 2, 3, 4, 5] to [3, 4, 5, 2, 1], then sgn(11ee7bbc_f5df_3c93_ae82_ade676104027_TB9661_11 ) = -1.
be the permutation that maps [1, 2, 3, 4, 5] to [3, 4, 5, 2, 1], then sgn(11ee7bbc_f5df_3c93_ae82_ade676104027_TB9661_11 ) = -1.
![Let be the permutation that maps [1, 2, 3, 4, 5] to [3, 4, 5, 2, 1], then sgn( ) = -1.](https://storage.examlex.com/TB9661/11ee7bbc_f5df_3c93_ae82_ade676104027_TB9661_11.jpg) be the permutation that maps [1, 2, 3, 4, 5] to [3, 4, 5, 2, 1], then sgn(11ee7bbc_f5df_3c93_ae82_ade676104027_TB9661_11 ) = -1.
be the permutation that maps [1, 2, 3, 4, 5] to [3, 4, 5, 2, 1], then sgn(11ee7bbc_f5df_3c93_ae82_ade676104027_TB9661_11 ) = -1.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
21
Expand and simplify: (2a dx + (b + 2a)dy + c dz)∧(a dx + 2b dy + c dz) - (2a2 - 2ab) ( a - b) dy∧dx . Express your answer in terms of the basis vectors dy∧dz, dz∧dx, and dx∧dy of 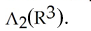

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
22
Let 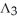 (
( 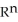 ) be the vector space of all 3-forms on
) be the vector space of all 3-forms on 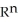 and
and 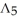 (
( 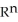 ) be the vector space of all 5-forms on
) be the vector space of all 5-forms on 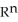 . If
. If 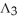 (
( 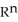 ) and
) and 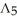 (
( 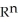 ) have the same dimension, find n.
) have the same dimension, find n.
A) 2
B) 4
C) 8
D) 15
E) 8 or -1
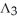 (
( 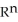 ) be the vector space of all 3-forms on
) be the vector space of all 3-forms on 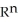 and
and 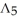 (
( 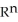 ) be the vector space of all 5-forms on
) be the vector space of all 5-forms on 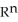 . If
. If 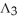 (
( 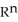 ) and
) and 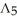 (
( 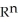 ) have the same dimension, find n.
) have the same dimension, find n.A) 2
B) 4
C) 8
D) 15
E) 8 or -1

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
23
Let η = F1 dy∧dz - F2 dx∧dz+ F3 dx∧dy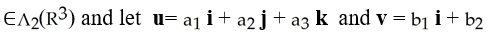 j + b3k
j + b3k
be vectors in . If η is identified by the vector w = F1 i + F2 j + F3 k then η (u, v) is equal to
A) w . (u + v)
B) w . (u × v)
C) w. (v - u)
D) w . (v × u)
E) w × (u × v)
 j + b3k
j + b3kbe vectors in . If η is identified by the vector w = F1 i + F2 j + F3 k then η (u, v) is equal to
A) w . (u + v)
B) w . (u × v)
C) w. (v - u)
D) w . (v × u)
E) w × (u × v)

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
24
Let  (
(  ), 1 k n be the vector space of all k-forms on
), 1 k n be the vector space of all k-forms on  and let
and let 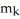 be the dimension of
be the dimension of 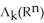 . Find
. Find 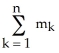 .
.
A)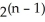
B)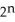
C)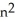
D)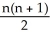
E)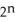 - 1
- 1
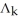 (
( 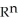 ), 1 k n be the vector space of all k-forms on
), 1 k n be the vector space of all k-forms on 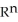 and let
and let 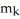 be the dimension of
be the dimension of 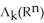 . Find
. Find 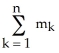 .
.A)
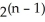
B)
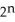
C)
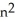
D)
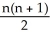
E)
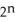 - 1
- 1
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
25
Let 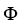 (x) =
(x) = 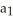 (x) d
(x) d 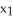 +
+ 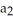 (x) d
(x) d 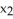 +
+ 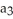 (x) d
(x) d 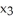 be a differential 1-form on a domain D in
be a differential 1-form on a domain D in 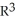 and let
and let 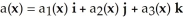 . The value of 11ee7bbd_2d92_9334_ae82_4706b097eca0_TB9661_11 (x) on a vector v
. The value of 11ee7bbd_2d92_9334_ae82_4706b097eca0_TB9661_11 (x) on a vector v 
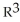 is equal to
is equal to
A) 11ee7bbd_2d92_9334_ae82_4706b097eca0_TB9661_11 (x)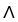 v
v
B) a(x) . v
C) a(x) × v
D) a(x) + v
E) v × a(x)
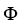 (x) =
(x) = 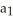 (x) d
(x) d 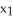 +
+ 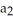 (x) d
(x) d 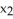 +
+ 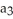 (x) d
(x) d 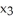 be a differential 1-form on a domain D in
be a differential 1-form on a domain D in 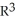 and let
and let 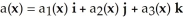 . The value of 11ee7bbd_2d92_9334_ae82_4706b097eca0_TB9661_11 (x) on a vector v
. The value of 11ee7bbd_2d92_9334_ae82_4706b097eca0_TB9661_11 (x) on a vector v 
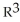 is equal to
is equal toA) 11ee7bbd_2d92_9334_ae82_4706b097eca0_TB9661_11 (x)
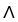 v
vB) a(x) . v
C) a(x) × v
D) a(x) + v
E) v × a(x)

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
26
Let 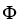 be a differential k-form and
be a differential k-form and 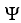 be a differential
be a differential 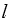 -form on a domain D
-form on a domain D 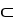
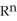 and letd(11ee7bbd_9e7e_0bb6_ae82_bb619a089092_TB9661_11
and letd(11ee7bbd_9e7e_0bb6_ae82_bb619a089092_TB9661_11 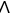 11ee7bbd_b7c7_e467_ae82_c37bb85a20c0_TB9661_11 )
11ee7bbd_b7c7_e467_ae82_c37bb85a20c0_TB9661_11 ) 
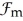 (D). Express m in terms of k and l.
(D). Express m in terms of k and l.
A) m = k + 11ee7bbe_0158_713a_ae82_97ce6608d721_TB9661_11
B) m = k 11ee7bbe_0158_713a_ae82_97ce6608d721_TB9661_11
C) m = k + 11ee7bbe_0158_713a_ae82_97ce6608d721_TB9661_11 + 2
D) m = k + 11ee7bbe_0158_713a_ae82_97ce6608d721_TB9661_11 + 1
E) m = k 11ee7bbe_0158_713a_ae82_97ce6608d721_TB9661_11 + 1
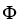 be a differential k-form and
be a differential k-form and 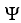 be a differential
be a differential  -form on a domain D
-form on a domain D 
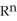 and letd(11ee7bbd_9e7e_0bb6_ae82_bb619a089092_TB9661_11
and letd(11ee7bbd_9e7e_0bb6_ae82_bb619a089092_TB9661_11 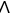 11ee7bbd_b7c7_e467_ae82_c37bb85a20c0_TB9661_11 )
11ee7bbd_b7c7_e467_ae82_c37bb85a20c0_TB9661_11 ) 
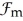 (D). Express m in terms of k and l.
(D). Express m in terms of k and l.A) m = k + 11ee7bbe_0158_713a_ae82_97ce6608d721_TB9661_11
B) m = k 11ee7bbe_0158_713a_ae82_97ce6608d721_TB9661_11
C) m = k + 11ee7bbe_0158_713a_ae82_97ce6608d721_TB9661_11 + 2
D) m = k + 11ee7bbe_0158_713a_ae82_97ce6608d721_TB9661_11 + 1
E) m = k 11ee7bbe_0158_713a_ae82_97ce6608d721_TB9661_11 + 1

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
27
Let 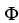 = 4xz
= 4xz 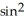 (y) dy
(y) dy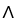 dz + z(2y + sin(2y)) dz11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11dx + (yz - 2
dz + z(2y + sin(2y)) dz11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11dx + (yz - 2 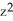 ) dx11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11dy. Find d11ee7bbe_8ef5_094b_ae82_6b47a89a60fc_TB9661_11 .
) dx11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11dy. Find d11ee7bbe_8ef5_094b_ae82_6b47a89a60fc_TB9661_11 .
A) (y - 8z) dx dz
dz
B) (8z - y) dx11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11dy11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11dz
C) (y - 4zcos(2y)) dx11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11dy11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11dz
D) y
E) ydx11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11dy11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11dz
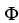 = 4xz
= 4xz 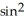 (y) dy
(y) dy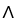 dz + z(2y + sin(2y)) dz11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11dx + (yz - 2
dz + z(2y + sin(2y)) dz11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11dx + (yz - 2 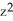 ) dx11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11dy. Find d11ee7bbe_8ef5_094b_ae82_6b47a89a60fc_TB9661_11 .
) dx11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11dy. Find d11ee7bbe_8ef5_094b_ae82_6b47a89a60fc_TB9661_11 .A) (y - 8z) dx
 dz
dzB) (8z - y) dx11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11dy11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11dz
C) (y - 4zcos(2y)) dx11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11dy11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11dz
D) y
E) ydx11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11dy11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11dz

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
28
Let 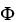 = xdx + vdv,
= xdx + vdv, 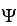 =
= 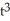 dy
dy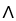 dw,
dw, 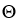 =
= 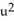 dz11ee7bbf_c537_273d_ae82_09ae839f29a0_TB9661_11 dv11ee7bbf_c537_273d_ae82_09ae839f29a0_TB9661_11 du be differential forms in a domain D
dz11ee7bbf_c537_273d_ae82_09ae839f29a0_TB9661_11 dv11ee7bbf_c537_273d_ae82_09ae839f29a0_TB9661_11 du be differential forms in a domain D 
 .Find d(11ee7bbf_ebe2_23df_ae82_0565ecd758af_TB9661_11
.Find d(11ee7bbf_ebe2_23df_ae82_0565ecd758af_TB9661_11 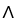 11ee7bc0_041d_24a0_ae82_87f021afe142_TB9661_11 11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 11ee7bc0_3408_e781_ae82_7de18ff0ad45_TB9661_11 ).
11ee7bc0_041d_24a0_ae82_87f021afe142_TB9661_11 11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 11ee7bc0_3408_e781_ae82_7de18ff0ad45_TB9661_11 ).
A) 12ut dx11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dy11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dz11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dt11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 du11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dv11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dw
B) 6xut dx11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dy11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dz11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dt11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 du11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dv11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dw
C) 3x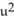
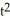 dx11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dy11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dz11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dt11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 du11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dv11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dw
dx11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dy11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dz11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dt11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 du11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dv11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dw
D) 3x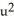
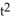
E) -3x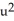
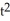 dx
dx du11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dv11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dw
du11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dv11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dw
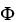 = xdx + vdv,
= xdx + vdv, 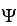 =
= 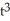 dy
dy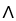 dw,
dw, 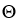 =
= 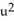 dz11ee7bbf_c537_273d_ae82_09ae839f29a0_TB9661_11 dv11ee7bbf_c537_273d_ae82_09ae839f29a0_TB9661_11 du be differential forms in a domain D
dz11ee7bbf_c537_273d_ae82_09ae839f29a0_TB9661_11 dv11ee7bbf_c537_273d_ae82_09ae839f29a0_TB9661_11 du be differential forms in a domain D 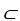
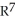 .Find d(11ee7bbf_ebe2_23df_ae82_0565ecd758af_TB9661_11
.Find d(11ee7bbf_ebe2_23df_ae82_0565ecd758af_TB9661_11 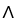 11ee7bc0_041d_24a0_ae82_87f021afe142_TB9661_11 11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 11ee7bc0_3408_e781_ae82_7de18ff0ad45_TB9661_11 ).
11ee7bc0_041d_24a0_ae82_87f021afe142_TB9661_11 11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 11ee7bc0_3408_e781_ae82_7de18ff0ad45_TB9661_11 ).A) 12ut dx11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dy11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dz11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dt11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 du11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dv11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dw
B) 6xut dx11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dy11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dz11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dt11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 du11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dv11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dw
C) 3x
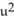
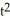 dx11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dy11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dz11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dt11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 du11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dv11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dw
dx11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dy11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dz11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dt11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 du11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dv11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dwD) 3x
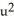
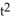
E) -3x
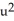
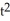 dx
dx du11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dv11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dw
du11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dv11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11 dw
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
29
Let 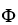 be a differential k-form and
be a differential k-form and 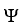 be a differential l-form on a domain D
be a differential l-form on a domain D 
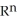 . State without proof a product rule for the exterior derivative of the wedge product 11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11
. State without proof a product rule for the exterior derivative of the wedge product 11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11 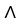 https://storage.examlex.com/TB9661/11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11.
https://storage.examlex.com/TB9661/11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11.
A) d11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11 11ee7bc1_6b1c_3825_ae82_afc27e21c96d_TB9661_11 11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11 +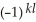 11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11 11ee7bc1_6b1c_3825_ae82_afc27e21c96d_TB9661_11 d11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11
11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11 11ee7bc1_6b1c_3825_ae82_afc27e21c96d_TB9661_11 d11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11
B) d11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11 11ee7bc1_6b1c_3825_ae82_afc27e21c96d_TB9661_11 11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11 + 11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11 11ee7bc1_6b1c_3825_ae82_afc27e21c96d_TB9661_11 d11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11
C) d11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11 11ee7bc1_6b1c_3825_ae82_afc27e21c96d_TB9661_11 11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11 +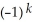 11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11 11ee7bc1_6b1c_3825_ae82_afc27e21c96d_TB9661_11 d11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11
11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11 11ee7bc1_6b1c_3825_ae82_afc27e21c96d_TB9661_11 d11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11
D) d11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11 11ee7bc1_6b1c_3825_ae82_afc27e21c96d_TB9661_11 11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11 +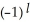 11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11 11ee7bc1_6b1c_3825_ae82_afc27e21c96d_TB9661_11 d11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11
11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11 11ee7bc1_6b1c_3825_ae82_afc27e21c96d_TB9661_11 d11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11
E) d11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11 11ee7bc1_6b1c_3825_ae82_afc27e21c96d_TB9661_11 11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11 +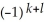 11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11 11ee7bc1_6b1c_3825_ae82_afc27e21c96d_TB9661_11 d11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11
11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11 11ee7bc1_6b1c_3825_ae82_afc27e21c96d_TB9661_11 d11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11
 be a differential k-form and
be a differential k-form and  be a differential l-form on a domain D
be a differential l-form on a domain D 
 . State without proof a product rule for the exterior derivative of the wedge product 11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11
. State without proof a product rule for the exterior derivative of the wedge product 11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11  https://storage.examlex.com/TB9661/11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11.
https://storage.examlex.com/TB9661/11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11.A) d11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11 11ee7bc1_6b1c_3825_ae82_afc27e21c96d_TB9661_11 11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11 +
 11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11 11ee7bc1_6b1c_3825_ae82_afc27e21c96d_TB9661_11 d11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11
11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11 11ee7bc1_6b1c_3825_ae82_afc27e21c96d_TB9661_11 d11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11B) d11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11 11ee7bc1_6b1c_3825_ae82_afc27e21c96d_TB9661_11 11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11 + 11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11 11ee7bc1_6b1c_3825_ae82_afc27e21c96d_TB9661_11 d11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11
C) d11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11 11ee7bc1_6b1c_3825_ae82_afc27e21c96d_TB9661_11 11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11 +
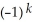 11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11 11ee7bc1_6b1c_3825_ae82_afc27e21c96d_TB9661_11 d11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11
11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11 11ee7bc1_6b1c_3825_ae82_afc27e21c96d_TB9661_11 d11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11D) d11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11 11ee7bc1_6b1c_3825_ae82_afc27e21c96d_TB9661_11 11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11 +
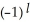 11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11 11ee7bc1_6b1c_3825_ae82_afc27e21c96d_TB9661_11 d11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11
11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11 11ee7bc1_6b1c_3825_ae82_afc27e21c96d_TB9661_11 d11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11E) d11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11 11ee7bc1_6b1c_3825_ae82_afc27e21c96d_TB9661_11 11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11 +
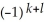 11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11 11ee7bc1_6b1c_3825_ae82_afc27e21c96d_TB9661_11 d11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11
11ee7bc0_83e8_98e2_ae82_39e0b41feeac_TB9661_11 11ee7bc1_6b1c_3825_ae82_afc27e21c96d_TB9661_11 d11ee7bc1_2249_2ef3_ae82_ad8c0cfa69a8_TB9661_11
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
30
Let 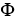 be a differential k-form,
be a differential k-form, 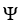 be a differential l-form, and
be a differential l-form, and 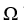 be an m-form on a domain D
be an m-form on a domain D 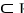
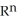 . Find an expression for a product rule for the exterior derivative of the wedge product 11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11
. Find an expression for a product rule for the exterior derivative of the wedge product 11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 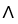 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 .
11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 .
A) d(11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 ) = (d11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 )11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 + 11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 d(11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 )11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 + 11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 d(11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 )
d(11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 )
B) d(11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 ) = (d11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 )11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 (d11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 )11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 (d11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 )
C) d(11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 ) =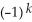 (d11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 )11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 +
(d11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 )11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 + 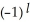 11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 d(11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 )11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 +
11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 d(11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 )11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 + 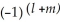 11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 d( 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 )
11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 d( 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 )
D) d(11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 ) = (d11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 )11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 +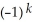 11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 d(11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 )11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 +
11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 d(11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 )11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 + 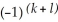 11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 d(11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 )
11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 d(11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 )
E) d(11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 ) = (d11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 )11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 +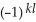 11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 d(11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 )11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 +
11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 d(11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 )11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 + 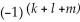 11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 d(11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 )
11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 d(11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 )
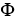 be a differential k-form,
be a differential k-form, 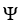 be a differential l-form, and
be a differential l-form, and 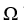 be an m-form on a domain D
be an m-form on a domain D 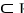
 . Find an expression for a product rule for the exterior derivative of the wedge product 11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11
. Find an expression for a product rule for the exterior derivative of the wedge product 11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11  11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 .
11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 .A) d(11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 ) = (d11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 )11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 + 11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 d(11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 )11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 + 11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11
 d(11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 )
d(11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 )B) d(11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 ) = (d11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 )11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 (d11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 )11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 (d11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 )
C) d(11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 ) =
 (d11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 )11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 +
(d11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 )11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 +  11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 d(11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 )11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 +
11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 d(11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 )11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 + 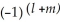 11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 d( 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 )
11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 d( 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 )D) d(11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 ) = (d11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 )11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 +
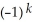 11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 d(11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 )11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 +
11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 d(11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 )11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 + 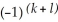 11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 d(11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 )
11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 d(11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 )E) d(11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 ) = (d11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 )11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 +
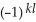 11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 d(11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 )11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 +
11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 d(11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 )11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 + 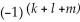 11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 d(11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 )
11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 d(11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 )
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
31
Let g(x) be a differential 0-form on a domain D in 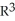 . If dg(x) =
. If dg(x) = 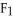 (x) dx+
(x) dx+ 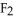 (x) dy +
(x) dy + 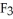 (x) dz, then the vector field
(x) dz, then the vector field 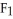 (x) i +
(x) i + 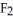 (x) j +
(x) j + 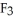 (x) k is equal to
(x) k is equal to
A) grad (g(x))
B) div(g(x))
C) curl ( g(x))
D) × (g(x))
E) (g(x)) g(x)
g(x)
 . If dg(x) =
. If dg(x) = 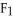 (x) dx+
(x) dx+ 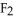 (x) dy +
(x) dy + 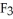 (x) dz, then the vector field
(x) dz, then the vector field 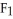 (x) i +
(x) i + 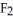 (x) j +
(x) j + 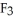 (x) k is equal to
(x) k is equal toA) grad (g(x))
B) div(g(x))
C) curl ( g(x))
D) × (g(x))
E) (g(x))
 g(x)
g(x)
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
32
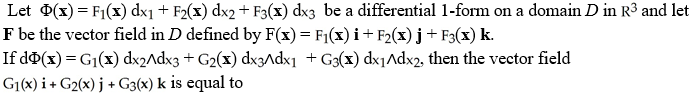
A) div( F)
B) div(F)
C) grad(F)
D) curl(F)
E)
 F
F
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
33
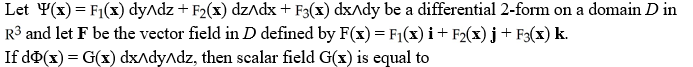
A) F .
B) div(F)
C) F . F
D) (F × ) . F
E)
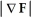

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
34
Let 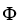 be a differential k-form and
be a differential k-form and 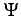 be a differential l-form on a domain D
be a differential l-form on a domain D 
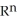 . Then
. Then 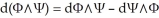 if and only if
if and only if
A) both k and l are even
B) both k and l are odd
C) k is even and l is odd
D) k is odd and l is even
E) k + l is even
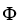 be a differential k-form and
be a differential k-form and 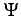 be a differential l-form on a domain D
be a differential l-form on a domain D 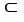
 . Then
. Then 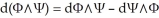 if and only if
if and only ifA) both k and l are even
B) both k and l are odd
C) k is even and l is odd
D) k is odd and l is even
E) k + l is even

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
35
You probably know by now that a differential k-form k 1 on a domain D 
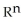 is very similar to a vector field on D, and hence a correspondence between the two may be established.Let
is very similar to a vector field on D, and hence a correspondence between the two may be established.Let 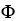 = F dx + G dy + H dz be a differential 1-form on a domain D
= F dx + G dy + H dz be a differential 1-form on a domain D 
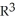 and let
and let 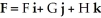 be the vector field corresponding to 11ee7bc6_e1d1_1134_ae82_9ddb9868f737_TB9661_11 . Using this set up, find the vector differential identity corresponding to the fact
be the vector field corresponding to 11ee7bc6_e1d1_1134_ae82_9ddb9868f737_TB9661_11 . Using this set up, find the vector differential identity corresponding to the fact  11ee7bc6_e1d1_1134_ae82_9ddb9868f737_TB9661_11 =
11ee7bc6_e1d1_1134_ae82_9ddb9868f737_TB9661_11 =  .
.
A) (divF) = 0
B) curl(F) = 0
C) div(curl F)= 0
D) F = 0
F = 0
E) curl(curl F) = 0
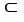
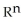 is very similar to a vector field on D, and hence a correspondence between the two may be established.Let
is very similar to a vector field on D, and hence a correspondence between the two may be established.Let 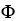 = F dx + G dy + H dz be a differential 1-form on a domain D
= F dx + G dy + H dz be a differential 1-form on a domain D 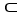
 and let
and let 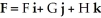 be the vector field corresponding to 11ee7bc6_e1d1_1134_ae82_9ddb9868f737_TB9661_11 . Using this set up, find the vector differential identity corresponding to the fact
be the vector field corresponding to 11ee7bc6_e1d1_1134_ae82_9ddb9868f737_TB9661_11 . Using this set up, find the vector differential identity corresponding to the fact  11ee7bc6_e1d1_1134_ae82_9ddb9868f737_TB9661_11 =
11ee7bc6_e1d1_1134_ae82_9ddb9868f737_TB9661_11 =  .
.A) (divF) = 0
B) curl(F) = 0
C) div(curl F)= 0
D)
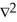 F = 0
F = 0E) curl(curl F) = 0

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
36
You probably know by now that a differential k-form k 1 on a domain D 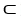
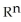 is very similar to a vector field on D, and hence a correspondence between the two may be established.For instance, we may set a correspondence between the 1-form
is very similar to a vector field on D, and hence a correspondence between the two may be established.For instance, we may set a correspondence between the 1-form 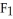 dx +
dx + 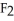 dy +
dy + 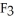 dz and the vector field F =
dz and the vector field F = 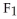 i +
i + 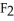 j +
j + 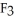 k. Using this setup, find the vector differential identity corresponding to the fact
k. Using this setup, find the vector differential identity corresponding to the fact 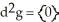 for any differential 0-form g on a domain D in
for any differential 0-form g on a domain D in 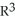 .
.
A) . ( g) = 0
B) × ( g) = 0
C)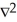 (g) = 0
(g) = 0
D) g = 0
E) ( g). ) = 0
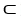
 is very similar to a vector field on D, and hence a correspondence between the two may be established.For instance, we may set a correspondence between the 1-form
is very similar to a vector field on D, and hence a correspondence between the two may be established.For instance, we may set a correspondence between the 1-form 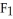 dx +
dx + 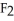 dy +
dy + 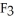 dz and the vector field F =
dz and the vector field F = 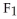 i +
i + 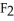 j +
j +  k. Using this setup, find the vector differential identity corresponding to the fact
k. Using this setup, find the vector differential identity corresponding to the fact 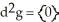 for any differential 0-form g on a domain D in
for any differential 0-form g on a domain D in 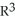 .
.A) . ( g) = 0
B) × ( g) = 0
C)
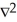 (g) = 0
(g) = 0D) g = 0
E) ( g). ) = 0

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
37
Let F(x, y) and G(x, y) be differential 0-forms on a domain D in 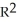 . Prove that(dF)∧(dG) =
. Prove that(dF)∧(dG) = 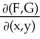 dx∧dy.
dx∧dy.
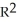 . Prove that(dF)∧(dG) =
. Prove that(dF)∧(dG) = 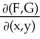 dx∧dy.
dx∧dy.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
38
If g is a differential 0-form and 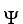 is a differential k-form on domain D
is a differential k-form on domain D 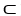
 , then
, then 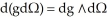 .
.
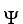 is a differential k-form on domain D
is a differential k-form on domain D 
 , then
, then 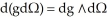 .
.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
39
Find a differential form  such that d11ee7bc7_4a83_9687_ae82_51ccf66be046_TB9661_11 = 3 dx
such that d11ee7bc7_4a83_9687_ae82_51ccf66be046_TB9661_11 = 3 dx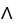 dy11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11 dzNote: answer is not unique.
dy11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11 dzNote: answer is not unique.
A) 4xdy11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11dz + ydz11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11dx -2z dy
dy
B) xdx + ydy + zdz
C) zdy11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11 dz + xdz11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11 dx + y11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11dx11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11 dy
D) 2ydy11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11 dz + 5zdz11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11 dx -4 x11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11dx 11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11 dy
E) (x + y + z ) dx11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11 dy11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11 dz
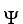 such that d11ee7bc7_4a83_9687_ae82_51ccf66be046_TB9661_11 = 3 dx
such that d11ee7bc7_4a83_9687_ae82_51ccf66be046_TB9661_11 = 3 dx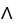 dy11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11 dzNote: answer is not unique.
dy11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11 dzNote: answer is not unique.A) 4xdy11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11dz + ydz11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11dx -2z
 dy
dyB) xdx + ydy + zdz
C) zdy11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11 dz + xdz11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11 dx + y11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11dx11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11 dy
D) 2ydy11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11 dz + 5zdz11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11 dx -4 x11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11dx 11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11 dy
E) (x + y + z ) dx11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11 dy11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11 dz

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
40
Prove that every smooth exterior derivative is a closed differential form.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
41
Which of the following is an antiderivative of 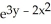 (3x + 4xy) dx
(3x + 4xy) dx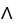 dy?
dy?
A)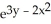 (9xdx -16
(9xdx -16 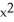 ydy)
ydy)
B)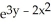 (x + y) dx?dy
(x + y) dx?dy
C)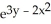 (xdx - ydy)
(xdx - ydy)
D)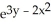 (x + y)
(x + y)
E) -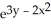 (xdx + ydy)
(xdx + ydy)
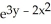 (3x + 4xy) dx
(3x + 4xy) dx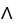 dy?
dy?A)
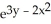 (9xdx -16
(9xdx -16 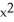 ydy)
ydy)B)
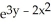 (x + y) dx?dy
(x + y) dx?dyC)
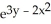 (xdx - ydy)
(xdx - ydy)D)
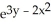 (x + y)
(x + y)E) -
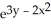 (xdx + ydy)
(xdx + ydy)
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
42
Let the differential 1-form 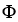 = zdy
= zdy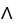 dz + xdz11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11 dx + ydx11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11 dy be defined in a star-like domain
dz + xdz11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11 dx + ydx11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11 dy be defined in a star-like domain 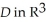 .(a) Is 11ee7bc8_9b9f_54e9_ae82_77ffde740b6c_TB9661_11 closed?(b) Is 11ee7bc8_9b9f_54e9_ae82_77ffde740b6c_TB9661_11 exact on D? If so, find a differential 1-form
.(a) Is 11ee7bc8_9b9f_54e9_ae82_77ffde740b6c_TB9661_11 closed?(b) Is 11ee7bc8_9b9f_54e9_ae82_77ffde740b6c_TB9661_11 exact on D? If so, find a differential 1-form 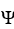 such that 11ee7bc8_9b9f_54e9_ae82_77ffde740b6c_TB9661_11 = d11ee7bc8_e3af_834b_ae82_7d811aed33cf_TB9661_11 .
such that 11ee7bc8_9b9f_54e9_ae82_77ffde740b6c_TB9661_11 = d11ee7bc8_e3af_834b_ae82_7d811aed33cf_TB9661_11 .
A) 11ee7bc8_9b9f_54e9_ae82_77ffde740b6c_TB9661_11 is neither closed nor exact
B) 11ee7bc8_9b9f_54e9_ae82_77ffde740b6c_TB9661_11 is both closed and exact, 11ee7bc8_e3af_834b_ae82_7d811aed33cf_TB9661_11 = (xz -
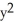 +
+ 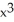 )dx + (yz + sin(z)) dz
)dx + (yz + sin(z)) dz
C) 11ee7bc8_9b9f_54e9_ae82_77ffde740b6c_TB9661_11 is both closed and exact,11ee7bc8_e3af_834b_ae82_7d811aed33cf_TB9661_11 = (xz +
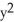 +
+ 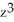 )dx + (yz + sin(x)) dy
)dx + (yz + sin(x)) dy
D) 11ee7bc8_9b9f_54e9_ae82_77ffde740b6c_TB9661_11 is closed but not exact
E) 11ee7bc8_9b9f_54e9_ae82_77ffde740b6c_TB9661_11 is both closed and exact, 11ee7bc8_e3af_834b_ae82_7d811aed33cf_TB9661_11= zxdx+ xydy + yzdz
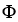 = zdy
= zdy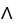 dz + xdz11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11 dx + ydx11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11 dy be defined in a star-like domain
dz + xdz11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11 dx + ydx11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11 dy be defined in a star-like domain 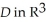 .(a) Is 11ee7bc8_9b9f_54e9_ae82_77ffde740b6c_TB9661_11 closed?(b) Is 11ee7bc8_9b9f_54e9_ae82_77ffde740b6c_TB9661_11 exact on D? If so, find a differential 1-form
.(a) Is 11ee7bc8_9b9f_54e9_ae82_77ffde740b6c_TB9661_11 closed?(b) Is 11ee7bc8_9b9f_54e9_ae82_77ffde740b6c_TB9661_11 exact on D? If so, find a differential 1-form 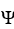 such that 11ee7bc8_9b9f_54e9_ae82_77ffde740b6c_TB9661_11 = d11ee7bc8_e3af_834b_ae82_7d811aed33cf_TB9661_11 .
such that 11ee7bc8_9b9f_54e9_ae82_77ffde740b6c_TB9661_11 = d11ee7bc8_e3af_834b_ae82_7d811aed33cf_TB9661_11 .A) 11ee7bc8_9b9f_54e9_ae82_77ffde740b6c_TB9661_11 is neither closed nor exact
B) 11ee7bc8_9b9f_54e9_ae82_77ffde740b6c_TB9661_11 is both closed and exact, 11ee7bc8_e3af_834b_ae82_7d811aed33cf_TB9661_11 = (xz -

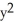 +
+  )dx + (yz + sin(z)) dz
)dx + (yz + sin(z)) dzC) 11ee7bc8_9b9f_54e9_ae82_77ffde740b6c_TB9661_11 is both closed and exact,11ee7bc8_e3af_834b_ae82_7d811aed33cf_TB9661_11 = (xz +

 +
+  )dx + (yz + sin(x)) dy
)dx + (yz + sin(x)) dyD) 11ee7bc8_9b9f_54e9_ae82_77ffde740b6c_TB9661_11 is closed but not exact
E) 11ee7bc8_9b9f_54e9_ae82_77ffde740b6c_TB9661_11 is both closed and exact, 11ee7bc8_e3af_834b_ae82_7d811aed33cf_TB9661_11= zxdx+ xydy + yzdz

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
43
Let the differential 2-form  = (3
= (3 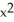 + 2xy + 6
+ 2xy + 6 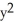 )dx
)dx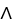 dy be defined in a star-like domain
dy be defined in a star-like domain 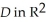 .
.
(a) Is 11ee7bc9_5715_4a9c_ae82_31f72d013c41_TB9661_11 closed?
(b) Is 11ee7bc9_5715_4a9c_ae82_31f72d013c41_TB9661_11 exact on D? If so, find a differential 1-form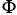 such that 11ee7bc9_5715_4a9c_ae82_31f72d013c41_TB9661_11 = d11ee7bc9_84dc_f4fe_ae82_1b41b7d4ea2f_TB9661_11 .
such that 11ee7bc9_5715_4a9c_ae82_31f72d013c41_TB9661_11 = d11ee7bc9_84dc_f4fe_ae82_1b41b7d4ea2f_TB9661_11 .
A) 11ee7bc9_5715_4a9c_ae82_31f72d013c41_TB9661_11 is closed but not exact
B) 11ee7bc9_5715_4a9c_ae82_31f72d013c41_TB9661_11 is both closed and exact, 11ee7bc9_84dc_f4fe_ae82_1b41b7d4ea2f_TB9661_11 = - (x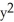 + 2
+ 2 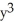 )dx +
)dx + 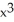 dy
dy
C) 11ee7bc9_5715_4a9c_ae82_31f72d013c41_TB9661_11 is neither closed nor exact
D)11ee7bc9_5715_4a9c_ae82_31f72d013c41_TB9661_11 is both closed and exact, 11ee7bc9_84dc_f4fe_ae82_1b41b7d4ea2f_TB9661_11 = (x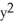 + 2
+ 2 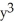 )dx +
)dx + 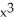 dy
dy
E) 11ee7bc9_5715_4a9c_ae82_31f72d013c41_TB9661_11 is both closed and exact, 11ee7bc9_84dc_f4fe_ae82_1b41b7d4ea2f_TB9661_11 =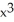 dx - (x
dx - (x  + 2
+ 2  )dy
)dy
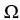 = (3
= (3  + 2xy + 6
+ 2xy + 6 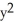 )dx
)dx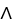 dy be defined in a star-like domain
dy be defined in a star-like domain 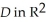 .
. (a) Is 11ee7bc9_5715_4a9c_ae82_31f72d013c41_TB9661_11 closed?
(b) Is 11ee7bc9_5715_4a9c_ae82_31f72d013c41_TB9661_11 exact on D? If so, find a differential 1-form
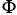 such that 11ee7bc9_5715_4a9c_ae82_31f72d013c41_TB9661_11 = d11ee7bc9_84dc_f4fe_ae82_1b41b7d4ea2f_TB9661_11 .
such that 11ee7bc9_5715_4a9c_ae82_31f72d013c41_TB9661_11 = d11ee7bc9_84dc_f4fe_ae82_1b41b7d4ea2f_TB9661_11 .A) 11ee7bc9_5715_4a9c_ae82_31f72d013c41_TB9661_11 is closed but not exact
B) 11ee7bc9_5715_4a9c_ae82_31f72d013c41_TB9661_11 is both closed and exact, 11ee7bc9_84dc_f4fe_ae82_1b41b7d4ea2f_TB9661_11 = - (x
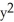 + 2
+ 2 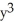 )dx +
)dx +  dy
dyC) 11ee7bc9_5715_4a9c_ae82_31f72d013c41_TB9661_11 is neither closed nor exact
D)11ee7bc9_5715_4a9c_ae82_31f72d013c41_TB9661_11 is both closed and exact, 11ee7bc9_84dc_f4fe_ae82_1b41b7d4ea2f_TB9661_11 = (x
 + 2
+ 2 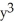 )dx +
)dx + 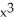 dy
dyE) 11ee7bc9_5715_4a9c_ae82_31f72d013c41_TB9661_11 is both closed and exact, 11ee7bc9_84dc_f4fe_ae82_1b41b7d4ea2f_TB9661_11 =
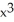 dx - (x
dx - (x 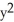 + 2
+ 2 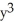 )dy
)dy
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
44
Let the differential 2-form 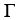 = xdy
= xdy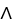 dz + ydz11ee7bc9_e7ae_ceff_ae82_cb591a35a817_TB9661_11 dx + (1 - 2z)dx11ee7bc9_e7ae_ceff_ae82_cb591a35a817_TB9661_11 dy be defined in a star-like domain
dz + ydz11ee7bc9_e7ae_ceff_ae82_cb591a35a817_TB9661_11 dx + (1 - 2z)dx11ee7bc9_e7ae_ceff_ae82_cb591a35a817_TB9661_11 dy be defined in a star-like domain 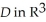 .
.
(a) Is 11ee7bca_0dd7_5530_ae82_83ba26f1ab04_TB9661_11 closed?
(b) Is 11ee7bca_0dd7_5530_ae82_83ba26f1ab04_TB9661_11 exact on D? If so, find a differential 1-form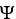 such that 11ee7bca_0dd7_5530_ae82_83ba26f1ab04_TB9661_11 = dhttps://storage.examlex.com/TB9661/11ee7bca_376e_ea71_ae82_a7b6e43e019b_TB9661_11.
such that 11ee7bca_0dd7_5530_ae82_83ba26f1ab04_TB9661_11 = dhttps://storage.examlex.com/TB9661/11ee7bca_376e_ea71_ae82_a7b6e43e019b_TB9661_11.
A) 11ee7bca_0dd7_5530_ae82_83ba26f1ab04_TB9661_11 is neither closed nor exact
B) 11ee7bca_0dd7_5530_ae82_83ba26f1ab04_TB9661_11 is both closed and exact, 11ee7bca_376e_ea71_ae82_a7b6e43e019b_TB9661_11 = ydx + 2xzdy - xydz
C) 11ee7bca_0dd7_5530_ae82_83ba26f1ab04_TB9661_11 is closed but not exact
D) 11ee7bca_0dd7_5530_ae82_83ba26f1ab04_TB9661_11 is exact but not closed, 11ee7bca_376e_ea71_ae82_a7b6e43e019b_TB9661_11 = ydx + 2xzdy + xydz
E) 11ee7bca_0dd7_5530_ae82_83ba26f1ab04_TB9661_11 is both closed and exact, 11ee7bca_376e_ea71_ae82_a7b6e43e019b_TB9661_11 = -ydx - 2xzdy - xydz
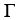 = xdy
= xdy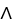 dz + ydz11ee7bc9_e7ae_ceff_ae82_cb591a35a817_TB9661_11 dx + (1 - 2z)dx11ee7bc9_e7ae_ceff_ae82_cb591a35a817_TB9661_11 dy be defined in a star-like domain
dz + ydz11ee7bc9_e7ae_ceff_ae82_cb591a35a817_TB9661_11 dx + (1 - 2z)dx11ee7bc9_e7ae_ceff_ae82_cb591a35a817_TB9661_11 dy be defined in a star-like domain 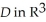 .
. (a) Is 11ee7bca_0dd7_5530_ae82_83ba26f1ab04_TB9661_11 closed?
(b) Is 11ee7bca_0dd7_5530_ae82_83ba26f1ab04_TB9661_11 exact on D? If so, find a differential 1-form
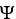 such that 11ee7bca_0dd7_5530_ae82_83ba26f1ab04_TB9661_11 = dhttps://storage.examlex.com/TB9661/11ee7bca_376e_ea71_ae82_a7b6e43e019b_TB9661_11.
such that 11ee7bca_0dd7_5530_ae82_83ba26f1ab04_TB9661_11 = dhttps://storage.examlex.com/TB9661/11ee7bca_376e_ea71_ae82_a7b6e43e019b_TB9661_11.A) 11ee7bca_0dd7_5530_ae82_83ba26f1ab04_TB9661_11 is neither closed nor exact
B) 11ee7bca_0dd7_5530_ae82_83ba26f1ab04_TB9661_11 is both closed and exact, 11ee7bca_376e_ea71_ae82_a7b6e43e019b_TB9661_11 = ydx + 2xzdy - xydz
C) 11ee7bca_0dd7_5530_ae82_83ba26f1ab04_TB9661_11 is closed but not exact
D) 11ee7bca_0dd7_5530_ae82_83ba26f1ab04_TB9661_11 is exact but not closed, 11ee7bca_376e_ea71_ae82_a7b6e43e019b_TB9661_11 = ydx + 2xzdy + xydz
E) 11ee7bca_0dd7_5530_ae82_83ba26f1ab04_TB9661_11 is both closed and exact, 11ee7bca_376e_ea71_ae82_a7b6e43e019b_TB9661_11 = -ydx - 2xzdy - xydz

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
45
Every (smooth) exact differential k-form on a domain D 
 is closed.
is closed.
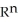 is closed.
is closed.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
46
If 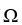 is a differential k-form, where k 1 is an even integer, then d(11ee7bca_9ca8_75a3_ae82_5bb03b7ccf94_TB9661_11
is a differential k-form, where k 1 is an even integer, then d(11ee7bca_9ca8_75a3_ae82_5bb03b7ccf94_TB9661_11 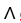 d11ee7bca_9ca8_75a3_ae82_5bb03b7ccf94_TB9661_11 ) =
d11ee7bca_9ca8_75a3_ae82_5bb03b7ccf94_TB9661_11 ) = 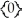 .
.
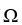 is a differential k-form, where k 1 is an even integer, then d(11ee7bca_9ca8_75a3_ae82_5bb03b7ccf94_TB9661_11
is a differential k-form, where k 1 is an even integer, then d(11ee7bca_9ca8_75a3_ae82_5bb03b7ccf94_TB9661_11 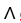 d11ee7bca_9ca8_75a3_ae82_5bb03b7ccf94_TB9661_11 ) =
d11ee7bca_9ca8_75a3_ae82_5bb03b7ccf94_TB9661_11 ) = 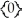 .
. 
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
47
Let [r, θ, z] be the cylindrical coordinates of a point in 3-space. Prove that rdr∧dθ∧dz = dx∧dy∧dz.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
48
Let Φ = (2xy - 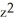 ) dx + (2yz +
) dx + (2yz + 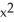 ) dy + (
) dy + ( 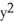 - 2zx) dz be a differential 1-form defined on a star-like domain D in
- 2zx) dz be a differential 1-form defined on a star-like domain D in 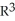 .
.
(a) Show that Φ is exact on D.
(b) Find a differential 0-form Ψsuch that Φ = dΨ on D.
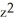 ) dx + (2yz +
) dx + (2yz + 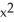 ) dy + (
) dy + ( 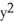 - 2zx) dz be a differential 1-form defined on a star-like domain D in
- 2zx) dz be a differential 1-form defined on a star-like domain D in 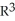 .
.(a) Show that Φ is exact on D.
(b) Find a differential 0-form Ψsuch that Φ = dΨ on D.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
49
Find the 2-volume of the 2-parallelogram in 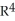 spanned by the vectors v1 = (0, - 1, -2, -1) and v2 = (1, 3, 7, 1).
spanned by the vectors v1 = (0, - 1, -2, -1) and v2 = (1, 3, 7, 1).
A) 18 units2
B) 36 units2
C) 6 units2
D) 9 units2
E) 8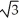 units2
units2
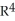 spanned by the vectors v1 = (0, - 1, -2, -1) and v2 = (1, 3, 7, 1).
spanned by the vectors v1 = (0, - 1, -2, -1) and v2 = (1, 3, 7, 1).A) 18 units2
B) 36 units2
C) 6 units2
D) 9 units2
E) 8
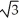 units2
units2
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
50
Find the 3-volume of the 3-parallelogram in 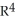 spanned by the vectors v1 = (2, 3, 1, 0),v2 = (0, -3, -2, 1), and v3 = (1, 1, 1, 1).
spanned by the vectors v1 = (2, 3, 1, 0),v2 = (0, -3, -2, 1), and v3 = (1, 1, 1, 1).
A) 10 units3
B) 50 units3
C) 100 units3
D) 540 units3
E) 6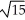 units3
units3
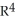 spanned by the vectors v1 = (2, 3, 1, 0),v2 = (0, -3, -2, 1), and v3 = (1, 1, 1, 1).
spanned by the vectors v1 = (2, 3, 1, 0),v2 = (0, -3, -2, 1), and v3 = (1, 1, 1, 1).A) 10 units3
B) 50 units3
C) 100 units3
D) 540 units3
E) 6
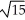 units3
units3
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
51
Find the 4-volume of the 4-parallelogram in 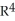 spanned by the vectors
spanned by the vectors 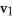 = (
= (  ,
,  ,
,  ,
,  ),
), 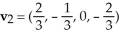 ,
, 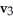 = (1, 0, 0, 0), and
= (1, 0, 0, 0), and 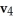 = (-
= (-  ,
,  , -
, -  ,
,  ).
).
A)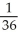
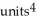
B)
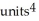
C)
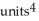
D)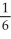
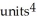
E)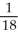
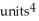
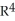 spanned by the vectors
spanned by the vectors 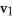 = (
= (  ,
,  ,
,  ,
,  ),
), 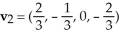 ,
, 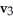 = (1, 0, 0, 0), and
= (1, 0, 0, 0), and 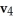 = (-
= (-  ,
,  , -
, -  ,
,  ).
).A)
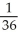
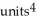
B)

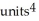
C)
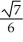
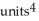
D)
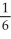
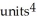
E)
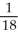
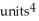

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
52
Find all values of the real number such that the 2-volume of the 2-parallelogram in 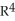 spanned by the vectors
spanned by the vectors 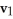 = (2, 0, 0, 1) and
= (2, 0, 0, 1) and 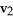 = (-2, , 8, 3) is equal to 22
= (-2, , 8, 3) is equal to 22 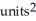 .
.
A) = ± 10
B) = ± 2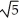
C) = ± 2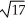
D) = ±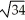
E) = ±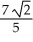
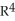 spanned by the vectors
spanned by the vectors 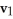 = (2, 0, 0, 1) and
= (2, 0, 0, 1) and 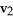 = (-2, , 8, 3) is equal to 22
= (-2, , 8, 3) is equal to 22 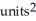 .
.A) = ± 10
B) = ± 2
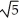
C) = ± 2
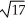
D) = ±
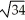
E) = ±
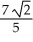

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
53
Find 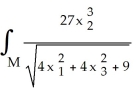 d
d 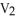 (x), where M is the 2-manifold in
(x), where M is the 2-manifold in 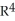 given parametrically by
given parametrically by 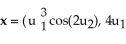 ,
, 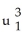 sin(2
sin(2 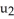 ), 3
), 3 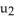 ) for 0 ≤
) for 0 ≤ 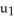 ≤ 1, 0 ≤
≤ 1, 0 ≤ 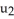 ≤ 1.
≤ 1.
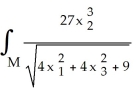 d
d 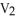 (x), where M is the 2-manifold in
(x), where M is the 2-manifold in  given parametrically by
given parametrically by 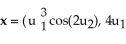 ,
, 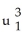 sin(2
sin(2 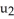 ), 3
), 3 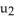 ) for 0 ≤
) for 0 ≤  ≤ 1, 0 ≤
≤ 1, 0 ≤ 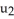 ≤ 1.
≤ 1.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
54
Find the 2-volume of the 2-manifold in 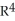 given parametrically by
given parametrically by 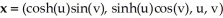 for 0 u 1, 0 v .
for 0 u 1, 0 v .
A)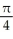 sinh(2)
sinh(2)
B) sinh(2) +
sinh(2) +
C)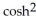 (1)
(1)
D) 0
E)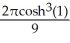
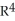 given parametrically by
given parametrically by 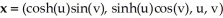 for 0 u 1, 0 v .
for 0 u 1, 0 v .A)
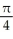 sinh(2)
sinh(2)B)
 sinh(2) +
sinh(2) + C)
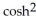 (1)
(1)D) 0
E)
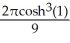

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
55
Let f be a smooth real value function over a domain D in 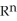 , then the graph xn+1 = f(
, then the graph xn+1 = f( 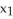 ,
, 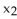 ,.....,
,....., 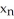 ) is
) is
A) a smooth (n - 1)-manifold in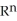
B) a smooth n-manifold in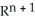
C) a smooth (n + 1)-manifold in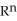
D) a smooth (n + 1)-manifold in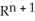
E) a smooth n-manifold in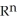
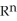 , then the graph xn+1 = f(
, then the graph xn+1 = f( 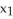 ,
, 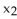 ,.....,
,....., 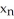 ) is
) isA) a smooth (n - 1)-manifold in
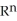
B) a smooth n-manifold in
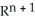
C) a smooth (n + 1)-manifold in
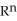
D) a smooth (n + 1)-manifold in
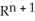
E) a smooth n-manifold in

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
56
The two equations z = 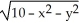 and z =
and z = 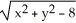 in
in 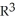 define a smooth manifold of dimension two in
define a smooth manifold of dimension two in 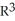 .
.
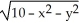 and z =
and z = 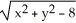 in
in 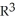 define a smooth manifold of dimension two in
define a smooth manifold of dimension two in 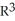 .
.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
57
One way to describe a smooth k-manifold M in 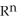 is to require its points
is to require its points 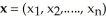 satisfy a set of (n - k) independent equations in (
satisfy a set of (n - k) independent equations in ( 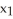 ,
, 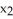 ,.....,
,....., 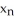 ).
).
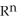 is to require its points
is to require its points 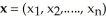 satisfy a set of (n - k) independent equations in (
satisfy a set of (n - k) independent equations in ( 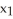 ,
, 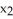 ,.....,
,....., 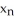 ).
).
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
58
Find 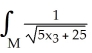 d
d 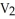 (x), where M is the 2-manifold in
(x), where M is the 2-manifold in 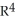 given parametrically by
given parametrically by 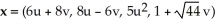 for 0 ≤ u ≤ 1, 0 ≤ v ≤ 1.
for 0 ≤ u ≤ 1, 0 ≤ v ≤ 1.
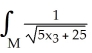 d
d 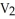 (x), where M is the 2-manifold in
(x), where M is the 2-manifold in 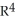 given parametrically by
given parametrically by 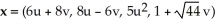 for 0 ≤ u ≤ 1, 0 ≤ v ≤ 1.
for 0 ≤ u ≤ 1, 0 ≤ v ≤ 1.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
59
The k-volume of a k-parallelogram in 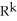 spanned by the k vectors,
spanned by the k vectors, 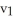 ,......,
,......, 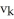
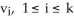 is given by det(A), where A is the k × k matrix whose columns are the components of the vectors.
is given by det(A), where A is the k × k matrix whose columns are the components of the vectors. 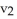
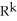 spanned by the k vectors,
spanned by the k vectors,  ,......,
,......, 
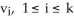 is given by det(A), where A is the k × k matrix whose columns are the components of the vectors.
is given by det(A), where A is the k × k matrix whose columns are the components of the vectors. 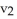

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
60
Let x = ( 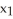 ,
, 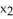 ,
, 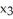 ) = (
) = ( 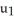 ,
, 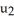 ,
, 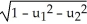 ), J(u) =
), J(u) = 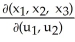 . Find det(
. Find det( 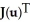 J(u)).
J(u)).
A)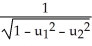
B) 1
C) d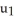 d
d 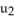
D)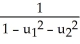 d
d 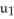 d
d 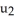
E)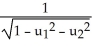 d
d 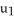 d
d 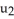
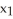 ,
, 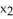 ,
, 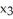 ) = (
) = ( 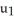 ,
, 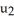 ,
, 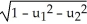 ), J(u) =
), J(u) = 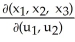 . Find det(
. Find det( 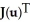 J(u)).
J(u)).A)
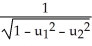
B) 1
C) d
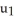 d
d 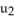
D)
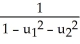 d
d 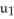 d
d 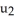
E)
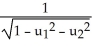 d
d 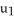 d
d 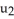

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
61
Calculate 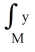 dx
dx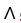 dz, where M is the surface given by z =
dz, where M is the surface given by z = 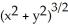 , 0 z 1, using the following parametrizations: (i) (x, y, z) = p(
, 0 z 1, using the following parametrizations: (i) (x, y, z) = p( 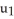 ,
, 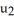 ) = (
) = ( 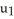 cos(
cos( 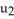 ),
), 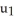 sin(
sin( 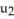 )
) 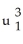 )
)
(ii) (x, y, z) = p(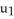 ,
, 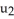 )= (
)= ( 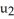 ,
, 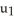 ,
, 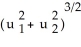 )
)
A) (i)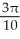 (ii) -
(ii) - 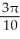
B) (i) (ii) 0
(ii) 0
C) (i)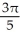 (ii) -
(ii) - 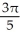
D) (i) 6 (ii) -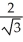
E) (i) -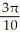 (ii)
(ii) 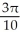
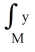 dx
dx dz, where M is the surface given by z =
dz, where M is the surface given by z = 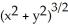 , 0 z 1, using the following parametrizations: (i) (x, y, z) = p(
, 0 z 1, using the following parametrizations: (i) (x, y, z) = p( 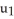 ,
, 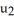 ) = (
) = ( 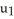 cos(
cos( 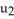 ),
), 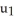 sin(
sin( 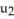 )
) 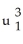 )
)(ii) (x, y, z) = p(
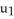 ,
, 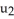 )= (
)= ( 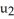 ,
, 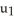 ,
, 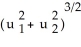 )
)A) (i)
 (ii) -
(ii) - 
B) (i)
 (ii) 0
(ii) 0C) (i)
 (ii) -
(ii) - 
D) (i) 6 (ii) -
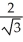
E) (i) -
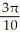 (ii)
(ii) 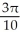

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
62
The 2-manifold M in R4 given by the equations 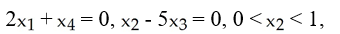 0 < x4 < 1,
0 < x4 < 1,
0 < < 1 has normals It is oriented by the 2-form
It is oriented by the 2-form
ω(x)( v1 , v2 ) = det( n1 n2 v1 v2 ). Let be a parametrization for M. Which of the following statements is true?
A) P is orientation preserving for M.
B) P does not determine an orientation for M.
C) P is orientation reversing for M, but no orientation preserving parametrization for M exists.
D) P is orientation reversing for M, but q(u) = ( , 5
, 5  ,
,  , -2
, -2 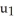 ) would be orientation preserving parametrization for M.
) would be orientation preserving parametrization for M.
E) P is orientation reversing for M, but q(u) = (-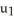 , 5
, 5 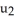 ,
, 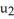 , 2
, 2 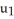 ) would be an orientation-preserving parametrization for M.
) would be an orientation-preserving parametrization for M.
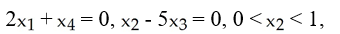 0 < x4 < 1,
0 < x4 < 1, 0 < < 1 has normals
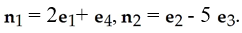 It is oriented by the 2-form
It is oriented by the 2-form ω(x)( v1 , v2 ) = det( n1 n2 v1 v2 ). Let be a parametrization for M. Which of the following statements is true?
A) P is orientation preserving for M.
B) P does not determine an orientation for M.
C) P is orientation reversing for M, but no orientation preserving parametrization for M exists.
D) P is orientation reversing for M, but q(u) = (
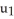 , 5
, 5 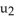 ,
, 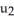 , -2
, -2  ) would be orientation preserving parametrization for M.
) would be orientation preserving parametrization for M.E) P is orientation reversing for M, but q(u) = (-
 , 5
, 5 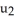 ,
, 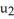 , 2
, 2 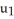 ) would be an orientation-preserving parametrization for M.
) would be an orientation-preserving parametrization for M.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
63
Find 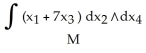 , where M is the 2-manifold in
, where M is the 2-manifold in  given parametrically by
given parametrically by 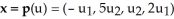 for 0 <
for 0 <  < 1, 0 <
< 1, 0 <  < 2.
< 2.
A) -130
B) 135
C) -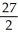
D) 130
E) -13
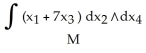 , where M is the 2-manifold in
, where M is the 2-manifold in  given parametrically by
given parametrically by 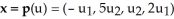 for 0 <
for 0 < 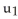 < 1, 0 <
< 1, 0 < 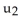 < 2.
< 2.A) -130
B) 135
C) -
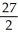
D) 130
E) -13

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
64
Evaluate the integral of 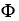 =
= 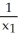 d
d 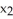
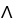 d
d 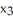 +
+ 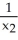 d
d 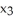 11ee7bcb_75db_a3b7_ae82_1108d245f507_TB9661_11 d
11ee7bcb_75db_a3b7_ae82_1108d245f507_TB9661_11 d 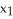 +
+ 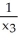 d
d 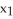 11ee7bcb_75db_a3b7_ae82_1108d245f507_TB9661_11 d
11ee7bcb_75db_a3b7_ae82_1108d245f507_TB9661_11 d 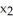 over the upper hemispherical surface
over the upper hemispherical surface 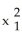 +
+ 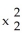 +
+ 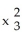 = 16,
= 16, 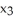 0.Note: There are two possible answers, depending on whether the parametrization used is orientation preserving or orientation reversing.
0.Note: There are two possible answers, depending on whether the parametrization used is orientation preserving or orientation reversing.
A) ±12
B) ± 4
C) ± 48
D) ± 6
E) ± 24
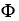 =
= 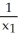 d
d 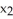
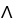 d
d 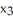 +
+ 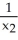 d
d 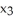 11ee7bcb_75db_a3b7_ae82_1108d245f507_TB9661_11 d
11ee7bcb_75db_a3b7_ae82_1108d245f507_TB9661_11 d 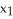 +
+ 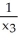 d
d 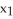 11ee7bcb_75db_a3b7_ae82_1108d245f507_TB9661_11 d
11ee7bcb_75db_a3b7_ae82_1108d245f507_TB9661_11 d 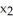 over the upper hemispherical surface
over the upper hemispherical surface 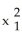 +
+ 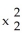 +
+ 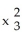 = 16,
= 16, 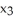 0.Note: There are two possible answers, depending on whether the parametrization used is orientation preserving or orientation reversing.
0.Note: There are two possible answers, depending on whether the parametrization used is orientation preserving or orientation reversing.A) ±12
B) ± 4
C) ± 48
D) ± 6
E) ± 24

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
65
If M is the part of the surface z = g(x, y) in 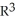 that lies above a closed region D in the
that lies above a closed region D in the 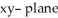 , then the integral of the differential 2-form
, then the integral of the differential 2-form 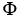 = f(x, y) dx
= f(x, y) dx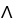 dy over M is independent of the function g.
dy over M is independent of the function g.
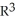 that lies above a closed region D in the
that lies above a closed region D in the  , then the integral of the differential 2-form
, then the integral of the differential 2-form 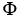 = f(x, y) dx
= f(x, y) dx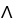 dy over M is independent of the function g.
dy over M is independent of the function g.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
66
Let M be the smooth 2-manifold  , x = p( ,
, x = p( ,  ) = (cos( )sin(11ee7bce_0cad_3050_ae82_0fc996929baa_TB9661_11 ), sin( )sin(11ee7bce_0cad_3050_ae82_0fc996929baa_TB9661_11 ), cos(11ee7bce_0cad_3050_ae82_0fc996929baa_TB9661_11 ),0 2 , and let
) = (cos( )sin(11ee7bce_0cad_3050_ae82_0fc996929baa_TB9661_11 ), sin( )sin(11ee7bce_0cad_3050_ae82_0fc996929baa_TB9661_11 ), cos(11ee7bce_0cad_3050_ae82_0fc996929baa_TB9661_11 ),0 2 , and let 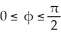 be a parametrization for M. If M is oriented by the differential 2-form
be a parametrization for M. If M is oriented by the differential 2-form 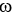 = zdx
= zdx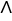 dy, determine whether the parametrization p is orientation preserving or orientation reversing for M.
dy, determine whether the parametrization p is orientation preserving or orientation reversing for M.
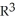 , x = p( ,
, x = p( , 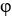 ) = (cos( )sin(11ee7bce_0cad_3050_ae82_0fc996929baa_TB9661_11 ), sin( )sin(11ee7bce_0cad_3050_ae82_0fc996929baa_TB9661_11 ), cos(11ee7bce_0cad_3050_ae82_0fc996929baa_TB9661_11 ),0 2 , and let
) = (cos( )sin(11ee7bce_0cad_3050_ae82_0fc996929baa_TB9661_11 ), sin( )sin(11ee7bce_0cad_3050_ae82_0fc996929baa_TB9661_11 ), cos(11ee7bce_0cad_3050_ae82_0fc996929baa_TB9661_11 ),0 2 , and let 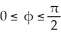 be a parametrization for M. If M is oriented by the differential 2-form
be a parametrization for M. If M is oriented by the differential 2-form  = zdx
= zdx dy, determine whether the parametrization p is orientation preserving or orientation reversing for M.
dy, determine whether the parametrization p is orientation preserving or orientation reversing for M. 
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
67
Consider the unit cube Q = 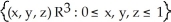 in
in 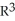 with the standard orientation given by
with the standard orientation given by 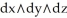 .Express the orientations of the bottom and the front faces of Q as differential 1-forms evaluated at the cross product of vectors u, v in
.Express the orientations of the bottom and the front faces of Q as differential 1-forms evaluated at the cross product of vectors u, v in 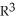 .
.
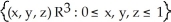 in
in 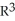 with the standard orientation given by
with the standard orientation given by 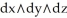 .Express the orientations of the bottom and the front faces of Q as differential 1-forms evaluated at the cross product of vectors u, v in
.Express the orientations of the bottom and the front faces of Q as differential 1-forms evaluated at the cross product of vectors u, v in 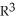 .
.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
68
Let S be a piece with boundary of a smooth 3-manifold in R4 (hypersurface) given by the equation  = g(
= g( 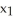 ,
, 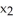 ,
, 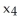 ) and let
) and let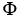 = d
= d 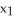
 d
d 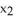 11ee7bcb_c6fc_6099_ae82_719973faadb8_TB9661_11 d
11ee7bcb_c6fc_6099_ae82_719973faadb8_TB9661_11 d 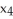 . Apart from sign due to orientation of S,
. Apart from sign due to orientation of S, 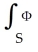 is equal to
is equal to
A) the 3-volume of the projection of S onto the hyperplane = 0
= 0
B) the 4-volume of the projection of S onto the hyperplane = 0
= 0
C)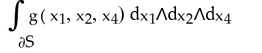
D)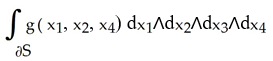
E) None of the above
 = g(
= g(  ,
,  ,
, 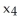 ) and let
) and let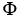 = d
= d 
 d
d 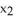 11ee7bcb_c6fc_6099_ae82_719973faadb8_TB9661_11 d
11ee7bcb_c6fc_6099_ae82_719973faadb8_TB9661_11 d 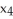 . Apart from sign due to orientation of S,
. Apart from sign due to orientation of S, 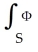 is equal to
is equal toA) the 3-volume of the projection of S onto the hyperplane
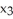 = 0
= 0B) the 4-volume of the projection of S onto the hyperplane
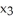 = 0
= 0C)
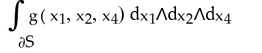
D)
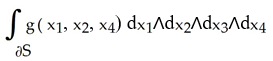
E) None of the above

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
69
Use the generalized Stokes's Theorem to find 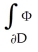 where
where 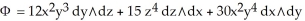 and
and  D is the oriented boundary of the domain
D is the oriented boundary of the domain 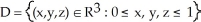 .
.
A) 5
B) 8
C) 240
D) 3
E) 37
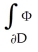 where
where 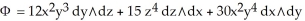 and
and  D is the oriented boundary of the domain
D is the oriented boundary of the domain 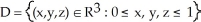 .
.A) 5
B) 8
C) 240
D) 3
E) 37

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
70
Use the generalized Stokes's Theorem to find 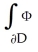 where
where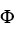 = 7x dy
= 7x dy dz + (3y + 2z) dz11ee7bcc_0cc6_216b_ae82_3f9133291a84_TB9661_11 dx - 9z dx11ee7bcc_0cc6_216b_ae82_3f9133291a84_TB9661_11 dy and
dz + (3y + 2z) dz11ee7bcc_0cc6_216b_ae82_3f9133291a84_TB9661_11 dx - 9z dx11ee7bcc_0cc6_216b_ae82_3f9133291a84_TB9661_11 dy and  D is the oriented boundary of the conical domain D =
D is the oriented boundary of the conical domain D = 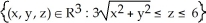 .
.
A) 8
B) 32
C) 24
D) 12
E) 4
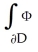 where
where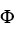 = 7x dy
= 7x dy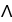 dz + (3y + 2z) dz11ee7bcc_0cc6_216b_ae82_3f9133291a84_TB9661_11 dx - 9z dx11ee7bcc_0cc6_216b_ae82_3f9133291a84_TB9661_11 dy and
dz + (3y + 2z) dz11ee7bcc_0cc6_216b_ae82_3f9133291a84_TB9661_11 dx - 9z dx11ee7bcc_0cc6_216b_ae82_3f9133291a84_TB9661_11 dy and 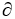 D is the oriented boundary of the conical domain D =
D is the oriented boundary of the conical domain D = 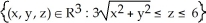 .
.A) 8
B) 32
C) 24
D) 12
E) 4

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
71
Integrate the differential 3-form  =
= 
 dx
dx dy11ee7bcc_8068_caae_ae82_1bce1a65fd1b_TB9661_11dz over the boundary of the 4-dimensional tetrahedron T =
dy11ee7bcc_8068_caae_ae82_1bce1a65fd1b_TB9661_11dz over the boundary of the 4-dimensional tetrahedron T = 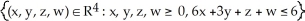 .
.
A) -648
B) -
C) -36
D) 648
E) 36
 =
= 
 dx
dx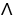 dy11ee7bcc_8068_caae_ae82_1bce1a65fd1b_TB9661_11dz over the boundary of the 4-dimensional tetrahedron T =
dy11ee7bcc_8068_caae_ae82_1bce1a65fd1b_TB9661_11dz over the boundary of the 4-dimensional tetrahedron T =  .
.A) -648
B) -
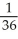
C) -36
D) 648
E) 36

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
72
Let C be the curve of intersection of the cylinder 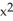 +
+ 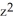 = 4 and the plane y = x + 1. Use the generalized Stokes's Theorem to evaluate
= 4 and the plane y = x + 1. Use the generalized Stokes's Theorem to evaluate 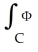 , where
, where 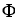 = -3
= -3 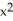 z dx + sin(y) dy + (3x
z dx + sin(y) dy + (3x 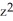 + x +7) dz.
+ x +7) dz.
A) 16
B) 28
C) 14
D) 20
E) 3
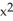 +
+ 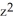 = 4 and the plane y = x + 1. Use the generalized Stokes's Theorem to evaluate
= 4 and the plane y = x + 1. Use the generalized Stokes's Theorem to evaluate 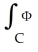 , where
, where 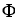 = -3
= -3  z dx + sin(y) dy + (3x
z dx + sin(y) dy + (3x  + x +7) dz.
+ x +7) dz.A) 16
B) 28
C) 14
D) 20
E) 3

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
73
State the Divergence Theorem and Stokes's Theorem in 3-space, and Green's Theorem in 2-space in terms of differential forms.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
74
Let Ω be the differential 3-form 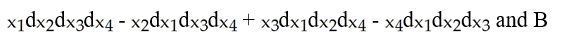 be the 4-dimensional ball of radius α in R4 ; that is
be the 4-dimensional ball of radius α in R4 ; that is
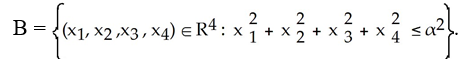
(a) Use the generalized Stokes's Theorem to evaluate
(b) Use part (a) to find the 4-volume of the ball.
Hint: You may use symmetry and the transformation , .
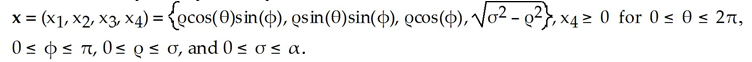
A) 4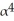
B)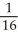
C)
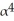
D) 2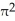
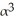
E)
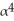
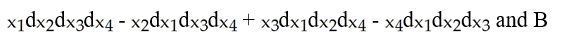 be the 4-dimensional ball of radius α in R4 ; that is
be the 4-dimensional ball of radius α in R4 ; that is 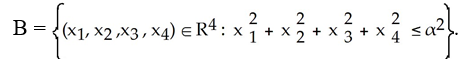
(a) Use the generalized Stokes's Theorem to evaluate
(b) Use part (a) to find the 4-volume of the ball.
Hint: You may use symmetry and the transformation , .
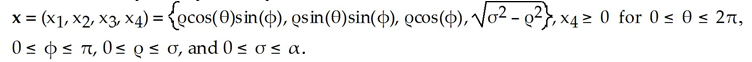
A) 4
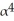
B)
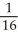
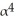
C)

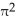
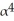
D) 2
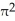
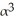
E)

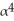

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
75
Let D be a closed bounded domain in  and lot Ψ = xdy∧dz + ydz∧dx + zdx∧dy. Show that the volume V of D is given by
and lot Ψ = xdy∧dz + ydz∧dx + zdx∧dy. Show that the volume V of D is given by 
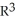 and lot Ψ = xdy∧dz + ydz∧dx + zdx∧dy. Show that the volume V of D is given by
and lot Ψ = xdy∧dz + ydz∧dx + zdx∧dy. Show that the volume V of D is given by 
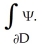

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
76
Integrate the differential (n -1)-form 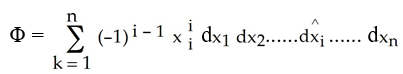 over the boundary of the n-dimensional cube
over the boundary of the n-dimensional cube 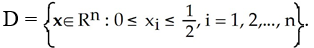
Note: The hat ∧ is used to indicate a missing component.
A)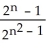
B)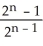
C)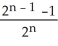
D)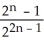
E)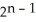
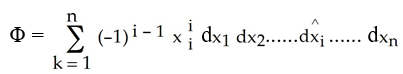 over the boundary of the n-dimensional cube
over the boundary of the n-dimensional cube 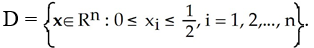
Note: The hat ∧ is used to indicate a missing component.
A)
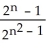
B)
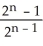
C)
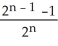
D)
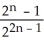
E)
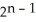

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck


