Exam 18: Differential Forms and Exterior Calculus
Exam 1: Preliminaries127 Questions
Exam 2: Limits and Continuity92 Questions
Exam 3: Differentiation131 Questions
Exam 4: Transcendental Functions129 Questions
Exam 5: More Applications of Differentiation130 Questions
Exam 6: Integration117 Questions
Exam 7: Techniques of Integration118 Questions
Exam 8: Applications of Integration139 Questions
Exam 9: Conics, Parametric Curves, and Polar Curves114 Questions
Exam 10: Sequences, Series, and Power Series125 Questions
Exam 11: Vectors and Coordinate Geometry in 3-Space119 Questions
Exam 12: Vector Functions and Curves87 Questions
Exam 13: Partial Differentiation104 Questions
Exam 14: Applications of Partial Derivatives67 Questions
Exam 15: Multiple Integration105 Questions
Exam 16: Vector Fields90 Questions
Exam 17: Vector Calculus92 Questions
Exam 18: Differential Forms and Exterior Calculus76 Questions
Exam 19: Ordinary Differential Equations135 Questions
Select questions type
Simplify a dx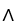 dy 11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11 dz + b dx
dy 11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11 dz + b dx dy + c dy11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11dz11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11dx + (a + b +c) dy
dy + c dy11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11dz11ee7bba_a357_125b_ae82_afb9ee65da13_TB9661_11dx + (a + b +c) dy dy.
dy.
Free
(Multiple Choice)
4.8/5  (36)
(36)
Correct Answer:
A
Find 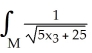 d
d 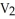 (x), where M is the 2-manifold in
(x), where M is the 2-manifold in 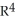 given parametrically by
given parametrically by 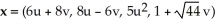 for 0 ≤ u ≤ 1, 0 ≤ v ≤ 1.
for 0 ≤ u ≤ 1, 0 ≤ v ≤ 1.
(Short Answer)
4.8/5  (27)
(27)
Let [r, θ, z] be the cylindrical coordinates of a point in 3-space. Prove that rdr∧dθ∧dz = dx∧dy∧dz.
(Essay)
4.7/5  (32)
(32)
If M is the part of the surface z = g(x, y) in 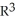 that lies above a closed region D in the
that lies above a closed region D in the 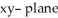 , then the integral of the differential 2-form
, then the integral of the differential 2-form 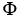 = f(x, y) dx
= f(x, y) dx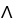 dy over M is independent of the function g.
dy over M is independent of the function g.
(True/False)
4.9/5  (32)
(32)
Let 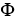 be a differential k-form,
be a differential k-form, 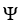 be a differential l-form, and
be a differential l-form, and 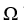 be an m-form on a domain D
be an m-form on a domain D 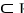
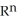 . Find an expression for a product rule for the exterior derivative of the wedge product 11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11
. Find an expression for a product rule for the exterior derivative of the wedge product 11ee7bc3_71c2_6b7a_ae82_2ff308d77e4f_TB9661_11 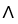 11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 .
11ee7bc3_ff64_cfeb_ae82_d9001ab9380d_TB9661_11 11ee7bc5_64fc_b24d_ae82_a1e274b00064_TB9661_11 11ee7bc4_a745_09fc_ae82_03df54d144ea_TB9661_11 .
(Multiple Choice)
4.8/5  (33)
(33)
Let k and n be integers such that 1 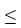 k 11ee7973_99f4_ef7a_88d3_478f26d4adc3_TB9661_11 n. Find the dimension of the vector space of all k-forms on
k 11ee7973_99f4_ef7a_88d3_478f26d4adc3_TB9661_11 n. Find the dimension of the vector space of all k-forms on 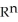 .
.
(Multiple Choice)
4.8/5  (31)
(31)
Let D be a closed bounded domain in 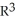 and lot Ψ = xdy∧dz + ydz∧dx + zdx∧dy. Show that the volume V of D is given by
and lot Ψ = xdy∧dz + ydz∧dx + zdx∧dy. Show that the volume V of D is given by 
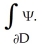
(Essay)
4.8/5  (27)
(27)
Let 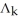 (
( 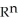 ), 1 k n be the vector space of all k-forms on
), 1 k n be the vector space of all k-forms on 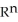 and let
and let 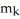 be the dimension of
be the dimension of 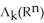 . Find
. Find 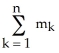 .
.
(Multiple Choice)
4.9/5  (31)
(31)
Let 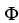 = 4xz
= 4xz 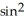 (y) dy
(y) dy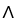 dz + z(2y + sin(2y)) dz11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11dx + (yz - 2
dz + z(2y + sin(2y)) dz11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11dx + (yz - 2 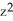 ) dx11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11dy. Find d11ee7bbe_8ef5_094b_ae82_6b47a89a60fc_TB9661_11 .
) dx11ee7bbe_ab46_077c_ae82_9ffd70004b08_TB9661_11dy. Find d11ee7bbe_8ef5_094b_ae82_6b47a89a60fc_TB9661_11 .
(Multiple Choice)
4.7/5  (37)
(37)
Find the 3-volume of the 3-parallelogram in 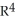 spanned by the vectors v1 = (2, 3, 1, 0),v2 = (0, -3, -2, 1), and v3 = (1, 1, 1, 1).
spanned by the vectors v1 = (2, 3, 1, 0),v2 = (0, -3, -2, 1), and v3 = (1, 1, 1, 1).
(Multiple Choice)
4.9/5  (34)
(34)
Let f be a smooth real value function over a domain D in 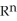 , then the graph xn+1 = f(
, then the graph xn+1 = f( 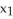 ,
, 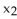 ,.....,
,....., 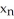 ) is
) is
(Multiple Choice)
4.8/5  (34)
(34)
The two equations z = 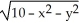 and z =
and z = 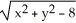 in
in 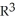 define a smooth manifold of dimension two in
define a smooth manifold of dimension two in 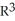 .
.
(True/False)
4.8/5  (38)
(38)
If g is a differential 0-form and 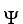 is a differential k-form on domain D
is a differential k-form on domain D 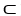
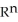 , then
, then 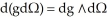 .
.
(True/False)
4.7/5  (35)
(35)
Let the differential 1-form 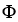 = zdy
= zdy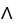 dz + xdz11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11 dx + ydx11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11 dy be defined in a star-like domain
dz + xdz11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11 dx + ydx11ee7bc7_61d1_9f38_ae82_4b21c548d46f_TB9661_11 dy be defined in a star-like domain 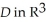 .(a) Is 11ee7bc8_9b9f_54e9_ae82_77ffde740b6c_TB9661_11 closed?(b) Is 11ee7bc8_9b9f_54e9_ae82_77ffde740b6c_TB9661_11 exact on D? If so, find a differential 1-form
.(a) Is 11ee7bc8_9b9f_54e9_ae82_77ffde740b6c_TB9661_11 closed?(b) Is 11ee7bc8_9b9f_54e9_ae82_77ffde740b6c_TB9661_11 exact on D? If so, find a differential 1-form 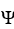 such that 11ee7bc8_9b9f_54e9_ae82_77ffde740b6c_TB9661_11 = d11ee7bc8_e3af_834b_ae82_7d811aed33cf_TB9661_11 .
such that 11ee7bc8_9b9f_54e9_ae82_77ffde740b6c_TB9661_11 = d11ee7bc8_e3af_834b_ae82_7d811aed33cf_TB9661_11 .
(Multiple Choice)
4.8/5  (41)
(41)
Use the generalized Stokes's Theorem to find 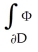 where
where 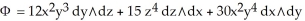 and
and 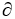 D is the oriented boundary of the domain
D is the oriented boundary of the domain 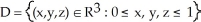 .
.
(Multiple Choice)
4.9/5  (33)
(33)
Expand and simplify: (2a dx + (b + 2a)dy + c dz)∧(a dx + 2b dy + c dz) - (2a2 - 2ab) ( a - b) dy∧dx . Express your answer in terms of the basis vectors dy∧dz, dz∧dx, and dx∧dy of 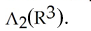
(Short Answer)
4.9/5  (36)
(36)
Showing 1 - 20 of 76
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)