Deck 17: Vector Calculus
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/92
Play
Full screen (f)
Deck 17: Vector Calculus
1
Compute the gradient of the function f(x, y) = 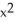 sin y +
sin y + 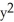 cos x.
cos x.
A) (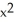 cos y - 2y cos x) i + (2x sin y +
cos y - 2y cos x) i + (2x sin y + 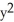 sin x) j
sin x) j
B) (2x sin y +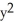 sin x) i + (
sin x) i + ( 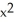 cos y - 2y cos x) j
cos y - 2y cos x) j
C) (2x sin y -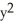 sin x) i + (
sin x) i + ( 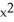 cos y + 2y cos x) j
cos y + 2y cos x) j
D) (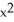 cos y + 2y cos x) i + (2x sin y -
cos y + 2y cos x) i + (2x sin y - 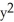 sin x) j
sin x) j
E) (2x sin y) i + (2y cos x) j
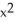 sin y +
sin y + 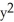 cos x.
cos x.A) (
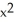 cos y - 2y cos x) i + (2x sin y +
cos y - 2y cos x) i + (2x sin y + 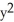 sin x) j
sin x) jB) (2x sin y +
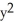 sin x) i + (
sin x) i + ( 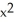 cos y - 2y cos x) j
cos y - 2y cos x) jC) (2x sin y -
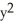 sin x) i + (
sin x) i + ( 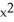 cos y + 2y cos x) j
cos y + 2y cos x) jD) (
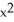 cos y + 2y cos x) i + (2x sin y -
cos y + 2y cos x) i + (2x sin y - 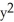 sin x) j
sin x) jE) (2x sin y) i + (2y cos x) j
(2x sin y - 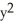 sin x) i + (
sin x) i + ( 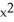 cos y + 2y cos x) j
cos y + 2y cos x) j
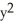 sin x) i + (
sin x) i + ( 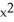 cos y + 2y cos x) j
cos y + 2y cos x) j 2
Find grad f(1, 0, -1) if f(x, y, z) = xy + yz.
A) i
B) j
C) 0
D) k
E) i + j + k
A) i
B) j
C) 0
D) k
E) i + j + k
0
3
If f(x, y, z) = 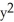 z + cos(z
z + cos(z 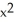 ), find
), find  f.
f.
A) 2zx sin(z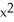 ) i + 2yz j + (
) i + 2yz j + ( 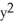 +
+ 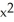 sin(z
sin(z 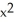 )) k
)) k
B) 2x sin(z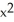 ) i + 2yz j + (
) i + 2yz j + ( 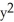 -
- 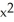 sin(z
sin(z 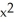 )) k
)) k
C) -2x sin(z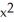 ) i + 2yz j + (
) i + 2yz j + ( 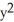 -
- 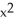 sin(z
sin(z 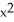 )) k
)) k
D) -2zx sin(z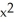 ) i + 2yz j + (
) i + 2yz j + ( 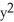 -
- 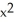 sin(z
sin(z 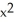 )) k
)) k
E) -2zx cos(z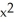 ) i + 2yz j + (
) i + 2yz j + ( 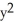 -
- 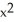 cos(z
cos(z 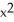 )) k
)) k
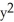 z + cos(z
z + cos(z 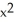 ), find
), find  f.
f.A) 2zx sin(z
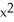 ) i + 2yz j + (
) i + 2yz j + ( 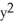 +
+ 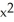 sin(z
sin(z 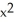 )) k
)) kB) 2x sin(z
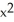 ) i + 2yz j + (
) i + 2yz j + ( 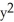 -
- 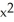 sin(z
sin(z 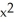 )) k
)) kC) -2x sin(z
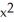 ) i + 2yz j + (
) i + 2yz j + ( 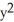 -
- 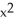 sin(z
sin(z 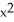 )) k
)) kD) -2zx sin(z
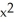 ) i + 2yz j + (
) i + 2yz j + ( 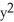 -
- 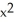 sin(z
sin(z 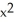 )) k
)) kE) -2zx cos(z
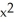 ) i + 2yz j + (
) i + 2yz j + ( 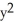 -
- 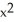 cos(z
cos(z 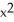 )) k
)) k-2zx sin(z 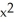 ) i + 2yz j + (
) i + 2yz j + ( 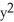 -
- 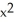 sin(z
sin(z 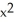 )) k
)) k
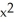 ) i + 2yz j + (
) i + 2yz j + ( 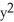 -
- 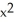 sin(z
sin(z 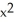 )) k
)) k 4
Compute div F for F = (2x + yz) i + ( 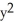 +
+ 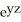 ) j + (x sin(z) +
) j + (x sin(z) + 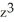 ) k.
) k.
A) 2 + 2y +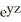 + cos(z) + 3
+ cos(z) + 3 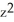
B) 2 + 2y + z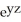 - x cos(z) + 3
- x cos(z) + 3 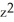
C) 2 + 2y + z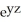 + x cos(z) + 3
+ x cos(z) + 3 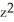
D) 2 + 2y + x cos(z)
E) 2 + 2y +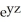 - cos(z) + 3
- cos(z) + 3 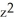
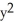 +
+ 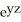 ) j + (x sin(z) +
) j + (x sin(z) + 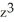 ) k.
) k.A) 2 + 2y +
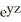 + cos(z) + 3
+ cos(z) + 3 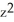
B) 2 + 2y + z
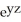 - x cos(z) + 3
- x cos(z) + 3 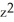
C) 2 + 2y + z
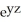 + x cos(z) + 3
+ x cos(z) + 3 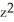
D) 2 + 2y + x cos(z)
E) 2 + 2y +
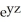 - cos(z) + 3
- cos(z) + 3 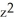

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
5
Compute curl F for F = (x - z) i + (y - x) j + (z - y) k.
A) - i + j - k
B) i + j + k
C) - i + j + k
D) i - j
E) 0
A) - i + j - k
B) i + j + k
C) - i + j + k
D) i - j
E) 0

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
6
Define the curl of a vector field F.
A) F ×
B)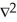 F
F
C) 11ee7bab_8c78_b929_ae82_a3f0e4bb6058_TB9661_11 × F
D) 11ee7bab_8c78_b929_ae82_a3f0e4bb6058_TB9661_11 . F
E) 11ee7bab_8c78_b929_ae82_a3f0e4bb6058_TB9661_11 F
A) F ×

B)
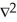 F
FC) 11ee7bab_8c78_b929_ae82_a3f0e4bb6058_TB9661_11 × F
D) 11ee7bab_8c78_b929_ae82_a3f0e4bb6058_TB9661_11 . F
E) 11ee7bab_8c78_b929_ae82_a3f0e4bb6058_TB9661_11 F

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
7
Let 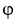 be a scalar field and F be a vector field, both assumed to be sufficiently smooth. Which of the following expressions is meaningless?
be a scalar field and F be a vector field, both assumed to be sufficiently smooth. Which of the following expressions is meaningless?
A) 11ee7bac_4a3a_9aaa_ae82_759e3f104991_TB9661_11 )
B)
C)
D) 11ee7bac_4a3a_9aaa_ae82_759e3f104991_TB9661_11 )
E)
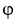 be a scalar field and F be a vector field, both assumed to be sufficiently smooth. Which of the following expressions is meaningless?
be a scalar field and F be a vector field, both assumed to be sufficiently smooth. Which of the following expressions is meaningless?A) 11ee7bac_4a3a_9aaa_ae82_759e3f104991_TB9661_11 )
B)
C)
D) 11ee7bac_4a3a_9aaa_ae82_759e3f104991_TB9661_11 )
E)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
8
Let 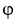 = arctan(x) - arctan(z) and
= arctan(x) - arctan(z) and 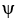 =
= 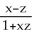 . Find a simplified expression for (11ee7bac_4a3a_9aaa_ae82_759e3f104991_TB9661_11 ) × (11ee7bac_77f1_7c2b_ae82_019616e1397c_TB9661_11 ) .
. Find a simplified expression for (11ee7bac_4a3a_9aaa_ae82_759e3f104991_TB9661_11 ) × (11ee7bac_77f1_7c2b_ae82_019616e1397c_TB9661_11 ) .
A)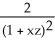 j
j
B) 0 (zero vector field)
C)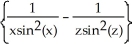 j
j
D) 0 (zero scalar field)
E) -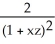 j
j
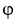 = arctan(x) - arctan(z) and
= arctan(x) - arctan(z) and 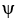 =
= 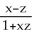 . Find a simplified expression for (11ee7bac_4a3a_9aaa_ae82_759e3f104991_TB9661_11 ) × (11ee7bac_77f1_7c2b_ae82_019616e1397c_TB9661_11 ) .
. Find a simplified expression for (11ee7bac_4a3a_9aaa_ae82_759e3f104991_TB9661_11 ) × (11ee7bac_77f1_7c2b_ae82_019616e1397c_TB9661_11 ) .A)
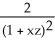 j
jB) 0 (zero vector field)
C)
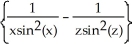 j
jD) 0 (zero scalar field)
E) -
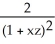 j
j
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
9
Compute for = 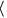 sin 2x, cos 2y, tan 2z
sin 2x, cos 2y, tan 2z 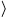 .
.
A) 2cos 2x + 2sin 2y +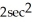 z
z
B) -cos 2x + sin 2y +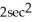 z
z
C) 2cos 2x - 2sin 2y +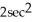 z
z
D) cos 2x + sin 2y +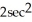 z
z
E) 2cos 2x - 2sin 2y + 2sec z
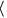 sin 2x, cos 2y, tan 2z
sin 2x, cos 2y, tan 2z 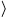 .
.A) 2cos 2x + 2sin 2y +
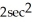 z
zB) -cos 2x + sin 2y +
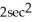 z
zC) 2cos 2x - 2sin 2y +
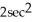 z
zD) cos 2x + sin 2y +
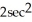 z
zE) 2cos 2x - 2sin 2y + 2sec z

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
10
Find https://storage.examlex.com/TB9661/ .F if F (x, y, z) =
.F if F (x, y, z) =  xy
xy 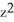 ,
, 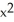 yz, -xyz
yz, -xyz  .
.
A) 2y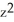 +
+ 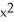 yz - xy
yz - xy
B) y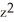 + 2xyz - xy
+ 2xyz - xy
C) y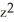 +
+ 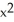 z - xy
z - xy
D) y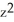 +
+ 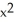 z + 2 xy
z + 2 xy
E) 2y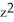 +
+ 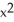 z + xy
z + xy
 .F if F (x, y, z) =
.F if F (x, y, z) = 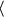 xy
xy 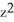 ,
, 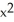 yz, -xyz
yz, -xyz  .
.A) 2y
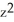 +
+ 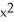 yz - xy
yz - xyB) y
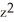 + 2xyz - xy
+ 2xyz - xyC) y
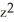 +
+ 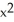 z - xy
z - xyD) y
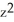 +
+ 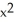 z + 2 xy
z + 2 xyE) 2y
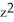 +
+ 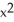 z + xy
z + xy
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
11
Compute the divergence for the vector field F = (xy + xz) i + (yz + yx) j + (zx + zy) k.
A) 2y + 2z + 2x
B) 3y + 2z + x
C) y + z + x
D) 2y -2 z + 2x
E) y + 2z + 3x
A) 2y + 2z + 2x
B) 3y + 2z + x
C) y + z + x
D) 2y -2 z + 2x
E) y + 2z + 3x

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
12
Find the acute angle (to the nearest degree) between the normals of the paraboloid z = x2 + y2 - 6 and the sphere x2 + y2 + z2 = 26 at the point (-3, 1, 4) on both surfaces.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
13
Calculate the divergence of the vector field F(x, y, z) = ( 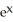 - xz) i + (z
- xz) i + (z 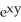 -
- 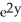 ) j - xy
) j - xy 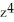 k.
k.
A)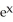 - z - zx
- z - zx 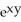 - 2
- 2 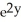 - y
- y 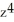
B)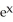 + zx
+ zx 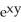 - 2
- 2 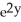 + 4xy
+ 4xy 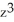
C)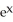 - z + zx
- z + zx 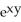 - 2
- 2 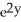 - 4xy
- 4xy 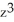
D)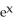 - z + zx
- z + zx 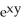 - 4xy
- 4xy 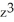
E)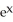 + zx
+ zx 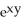 + 2
+ 2 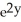 + 4xy
+ 4xy 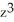
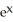 - xz) i + (z
- xz) i + (z 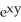 -
- 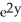 ) j - xy
) j - xy 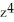 k.
k.A)
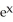 - z - zx
- z - zx 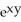 - 2
- 2 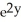 - y
- y 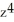
B)
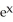 + zx
+ zx 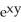 - 2
- 2 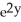 + 4xy
+ 4xy 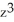
C)
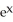 - z + zx
- z + zx 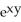 - 2
- 2 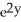 - 4xy
- 4xy 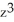
D)
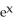 - z + zx
- z + zx 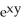 - 4xy
- 4xy 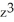
E)
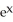 + zx
+ zx 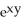 + 2
+ 2 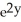 + 4xy
+ 4xy 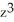

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
14
Calculate the curl of the vector field V = x sin y i + cos y j + xy k.
A) x i + y j - x cos y k
B) x i - y j + x cos y k
C) x i - y j - x cos y k
D) x i + y j + x cos y k
E) -x i + y j + y cos y k
A) x i + y j - x cos y k
B) x i - y j + x cos y k
C) x i - y j - x cos y k
D) x i + y j + x cos y k
E) -x i + y j + y cos y k

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
15
Calculate the divergence of the vector field F = 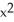 y i +
y i + 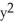 x j + xyz k.
x j + xyz k.
A) 5xy
B) 4xy + yz
C) 6xy
D) 2xy + 2yz + xz
E) 4xy + xz
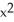 y i +
y i + 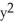 x j + xyz k.
x j + xyz k.A) 5xy
B) 4xy + yz
C) 6xy
D) 2xy + 2yz + xz
E) 4xy + xz

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
16
 . F = F . 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 for any sufficiently smooth vector field F.
. F = F . 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 for any sufficiently smooth vector field F.
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
17
Let w be a function of x, y, and z having continuous second partial derivatives.Calculate curl grad w in terms of those partials.
A)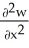 +
+ 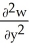 +
+ 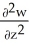
B)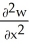 i +
i + 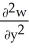 j +
j + 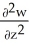 k
k
C)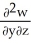 i +
i + 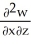 j +
j + 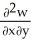 k
k
D) 0
E)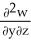 +
+ 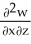 +
+ 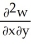
A)
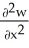 +
+ 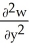 +
+ 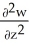
B)
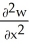 i +
i + 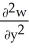 j +
j + 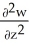 k
kC)
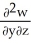 i +
i + 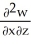 j +
j + 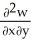 k
kD) 0
E)
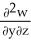 +
+ 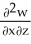 +
+ 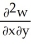

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
18
Let F = f(x, y, z) i + g(x, y, z) j + h(x, y, z) k be a vector field in 3-space whose components f, g, and h have continuous second partial derivatives. Calculate div curl F in terms of those partials.
A)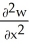 +
+ 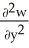 +
+ 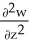
B) -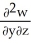 -
- 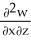 -
- 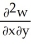
C)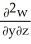 +
+ 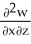 +
+ 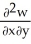
D) 0
E)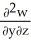 -
- 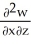 +
+ 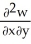
A)
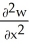 +
+ 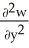 +
+ 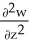
B) -
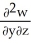 -
- 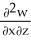 -
- 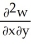
C)
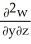 +
+ 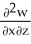 +
+ 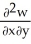
D) 0
E)
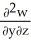 -
- 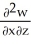 +
+ 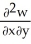

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
19
The divergence of a vector field F is defined by
A)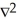 F
F
B) . F
. F
C) 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 F
D) 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 . (11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11F)
E) 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 × F
A)
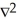 F
FB)
 . F
. FC) 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 F
D) 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 . (11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11F)
E) 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 × F

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
20
The curl of a vector field F is defined by
A) .(11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11F)
.(11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11F)
B) 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 × F
C)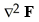
D) 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 F
E) 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 . F
A)
 .(11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11F)
.(11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11F)B) 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 × F
C)
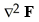
D) 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 F
E) 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 . F

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
21
Compute the divergence and the curl of the vector field r = x i + y j + z k.
A) . r = 2, 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 × r = 0
. r = 2, 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 × r = 0
B)11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 . r = 3, 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11× r = 0
C) 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 . r = 3, 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 × r = r
D) 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 . r = 1, 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 × r = 0
E) 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 . r = 2, 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 × r = r
A)
 . r = 2, 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 × r = 0
. r = 2, 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 × r = 0B)11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 . r = 3, 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11× r = 0
C) 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 . r = 3, 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 × r = r
D) 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 . r = 1, 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 × r = 0
E) 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 . r = 2, 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 × r = r

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
22
If r = x i + y j + z k and f(u) is any differentiable function of one variable, evaluate and simplify 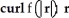 .
.
A) 0
B) r
C) 2r
D) 3r
E) 4r
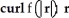 .
.A) 0
B) r
C) 2r
D) 3r
E) 4r

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
23
If r = x i + y j + z k and r = |r|, evaluate and simplify div 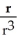 .
.
A) 0
B)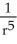
C)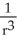
D)
E)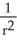
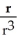 .
.A) 0
B)
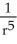
C)
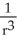
D)

E)
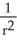

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
24
For r = x i + y j + z k, evaluate and simplify  .
. 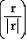 .
.
A)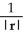
B)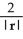
C)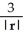
D) |r|
E) 0
 .
.  .
.A)
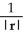
B)
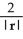
C)
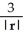
D) |r|
E) 0

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
25
Let B be a constant vector and let G(r) = (B × r) × r be a vector potential of the solenoidal vector field F. Find F.
A) F = B
B) F = r
C) F = r × B
D) F = 3(B × r)
E) F = (B × r)
(B × r)
A) F = B
B) F = r
C) F = r × B
D) F = 3(B × r)
E) F =
 (B × r)
(B × r)
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
26
Verify that the vector field F = (2x y2z2 - sin(x)sin(y)) i + (2 x2y z2+ cos(x)cos(y)) j + (2x2y2 z + ) k is conservative and find a scalar potential f(x, y, z) for it that satisfies f(0, 0, 0) = 1.
A)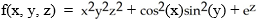
B) f(x, y, z) =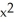
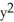
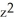 + cos(x)sin(y) +
+ cos(x)sin(y) + 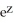 + 1
+ 1
C) f(x, y, z) =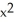
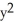
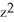 + sin(x)cos(y) +
+ sin(x)cos(y) + 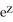 + 1
+ 1
D) f(x, y, z) =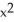
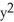
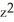 + cos(x)sin(y) +
+ cos(x)sin(y) + 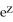
E) f(x, y, z) = xyz + cos(x)sin(y) +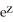
A)
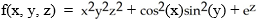
B) f(x, y, z) =
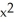
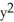
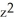 + cos(x)sin(y) +
+ cos(x)sin(y) + 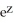 + 1
+ 1C) f(x, y, z) =
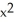
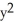
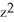 + sin(x)cos(y) +
+ sin(x)cos(y) + 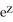 + 1
+ 1D) f(x, y, z) =
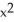
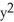
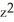 + cos(x)sin(y) +
+ cos(x)sin(y) + 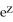
E) f(x, y, z) = xyz + cos(x)sin(y) +
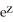

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
27
If the vector field H = f(r) r, r 0 is solenoidal, find an expression for f(r).
A) f(r) = c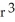 , where c is an arbitrary constant
, where c is an arbitrary constant
B) f(r) = c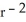 , where c is an arbitrary constant
, where c is an arbitrary constant
C) f(r) = c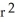 , where c is an arbitrary constant
, where c is an arbitrary constant
D) f(r) = c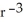 , where c is an arbitrary constant
, where c is an arbitrary constant
E) f(r) = c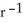 , where c is an arbitrary constant
, where c is an arbitrary constant
A) f(r) = c
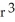 , where c is an arbitrary constant
, where c is an arbitrary constantB) f(r) = c
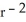 , where c is an arbitrary constant
, where c is an arbitrary constantC) f(r) = c
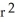 , where c is an arbitrary constant
, where c is an arbitrary constantD) f(r) = c
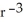 , where c is an arbitrary constant
, where c is an arbitrary constantE) f(r) = c
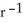 , where c is an arbitrary constant
, where c is an arbitrary constant
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
28
Show that div ( 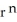 r) = (n + 3)
r) = (n + 3) 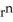 .You may use the following fact: grad (
.You may use the following fact: grad ( 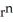 ) = n
) = n 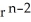 r
r
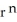 r) = (n + 3)
r) = (n + 3) 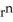 .You may use the following fact: grad (
.You may use the following fact: grad ( 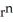 ) = n
) = n 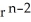 r
r
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
29
A vector field F is called in a domain D if
A)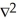 F = 0 in D
F = 0 in D
B) curl(F) = 0 in D
C) F =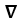
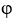 in D for some scalar field 11ee7bad_3b7e_852d_ae82_0ffea7b87591_TB9661_11
in D for some scalar field 11ee7bad_3b7e_852d_ae82_0ffea7b87591_TB9661_11
D) div(F) = 0 in D
E) grad(F) = 0 in D
A)
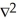 F = 0 in D
F = 0 in DB) curl(F) = 0 in D
C) F =
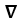
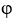 in D for some scalar field 11ee7bad_3b7e_852d_ae82_0ffea7b87591_TB9661_11
in D for some scalar field 11ee7bad_3b7e_852d_ae82_0ffea7b87591_TB9661_11D) div(F) = 0 in D
E) grad(F) = 0 in D

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
30
Find all values of the nonzero constant real numbers a, b, and c so that the vector field F = a cos( 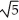 x + 2y )cosh (c z) i + b cos (
x + 2y )cosh (c z) i + b cos ( 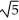 x + 2y)cosh (c z) j + c sin(
x + 2y)cosh (c z) j + c sin( 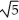 x + 2y)sinh(c z) k is both and .
x + 2y)sinh(c z) k is both and .
A) a = -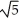 , b = -2, c = 3
, b = -2, c = 3
B) a =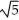 , b = 2, c = 2
, b = 2, c = 2
C) a = -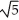 , b = -2, c =
, b = -2, c = 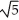 ± 2
± 2
D) a =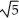 , b = 2, c = ± 3
, b = 2, c = ± 3
E) a =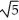 , b = -2, c = 9
, b = -2, c = 9
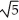 x + 2y )cosh (c z) i + b cos (
x + 2y )cosh (c z) i + b cos ( 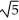 x + 2y)cosh (c z) j + c sin(
x + 2y)cosh (c z) j + c sin( 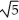 x + 2y)sinh(c z) k is both and .
x + 2y)sinh(c z) k is both and .A) a = -
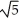 , b = -2, c = 3
, b = -2, c = 3B) a =
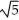 , b = 2, c = 2
, b = 2, c = 2C) a = -
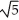 , b = -2, c =
, b = -2, c = 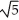 ± 2
± 2D) a =
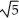 , b = 2, c = ± 3
, b = 2, c = ± 3E) a =
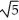 , b = -2, c = 9
, b = -2, c = 9
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
31
Verify that the vector field F = 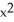 i + (1 - xy) j - xz k is solenoidal, and find a vector potential G for it having the form G(x, y, z) =
i + (1 - xy) j - xz k is solenoidal, and find a vector potential G for it having the form G(x, y, z) = 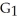 (x, y, z) i +
(x, y, z) i + 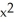 y k.
y k.
A) (xyz + z) i +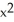 y k
y k
B) (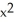 y + z) i +
y + z) i + 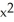 y k
y k
C) (xyz - z) i +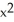 y k
y k
D) (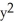 z - z) i +
z - z) i + 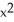 y k
y k
E) xyz i +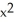 y k
y k
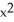 i + (1 - xy) j - xz k is solenoidal, and find a vector potential G for it having the form G(x, y, z) =
i + (1 - xy) j - xz k is solenoidal, and find a vector potential G for it having the form G(x, y, z) = 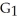 (x, y, z) i +
(x, y, z) i + 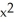 y k.
y k.A) (xyz + z) i +
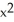 y k
y kB) (
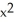 y + z) i +
y + z) i + 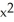 y k
y kC) (xyz - z) i +
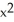 y k
y kD) (
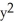 z - z) i +
z - z) i + 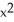 y k
y kE) xyz i +
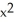 y k
y k
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
32
For what value of the constant C is the vector field F = 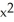 i + C(xy + yz) j +
i + C(xy + yz) j + 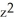 k. solenoidal?
k. solenoidal?
If C has that value, find a vector potential G for F having the form G(x, y, z) =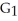 (x, y, z) i +
(x, y, z) i + 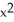 y k.
y k.
A) C = -2, G = y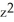 i +
i + 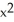 y k
y k
B) C = -2, G = - y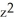 i +
i + 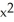 y k
y k
C) C = -2, G = x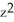 i +
i + 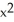 y k
y k
D) C = -2, G = - x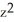 i +
i + 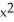 y k
y k
E) C = 2, G = y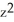 i +
i + 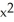 y k
y k
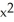 i + C(xy + yz) j +
i + C(xy + yz) j + 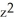 k. solenoidal?
k. solenoidal?If C has that value, find a vector potential G for F having the form G(x, y, z) =
 (x, y, z) i +
(x, y, z) i + 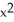 y k.
y k.A) C = -2, G = y
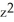 i +
i + 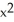 y k
y kB) C = -2, G = - y
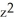 i +
i + 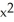 y k
y kC) C = -2, G = x
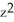 i +
i + 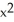 y k
y kD) C = -2, G = - x
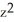 i +
i + 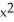 y k
y kE) C = 2, G = y
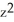 i +
i + 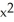 y k
y k
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
33
Show that there does not exist a twice continuously differentiable vector field G such that = x i + y j + z k.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
34
A vector field F satisfying the equation div F = 0 in domain D is called:
A) irrotational in D
B) a scalar potential
C) solenoidal in D
D) conservative in D
E) a vector potential
A) irrotational in D
B) a scalar potential
C) solenoidal in D
D) conservative in D
E) a vector potential

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
35
Let 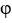 and F be sufficiently smooth scalar and vector fields, respectively.Express the well-known identity https://storage.examlex.com/TB9661/https://storage.examlex.com/TB9661/
and F be sufficiently smooth scalar and vector fields, respectively.Express the well-known identity https://storage.examlex.com/TB9661/https://storage.examlex.com/TB9661/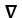 . (11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 F ) = (11ee7bad_7817_372f_ae82_a36163e56c30_TB9661_11 11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 ) . F + 11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 (11ee7bad_7817_372f_ae82_a36163e56c30_TB9661_11. F) using the notations grad , div or curl.
. (11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 F ) = (11ee7bad_7817_372f_ae82_a36163e56c30_TB9661_11 11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 ) . F + 11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 (11ee7bad_7817_372f_ae82_a36163e56c30_TB9661_11. F) using the notations grad , div or curl.
A) curl (11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 F) = grad (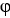 ) . F + 11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 div (F)
) . F + 11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 div (F)
B) div (11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 F) = curl (11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 ) . F + 11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 grad (F)
C) div (11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 F) = grad (11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 ) . F + 11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 div (F)
D) grad (11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 F) = div (11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 ) . F + 11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 curl (F)
E) curl (11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 F) = div (11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 ) . F +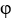 grad (F)
grad (F)
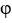 and F be sufficiently smooth scalar and vector fields, respectively.Express the well-known identity https://storage.examlex.com/TB9661/https://storage.examlex.com/TB9661/
and F be sufficiently smooth scalar and vector fields, respectively.Express the well-known identity https://storage.examlex.com/TB9661/https://storage.examlex.com/TB9661/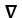 . (11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 F ) = (11ee7bad_7817_372f_ae82_a36163e56c30_TB9661_11 11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 ) . F + 11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 (11ee7bad_7817_372f_ae82_a36163e56c30_TB9661_11. F) using the notations grad , div or curl.
. (11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 F ) = (11ee7bad_7817_372f_ae82_a36163e56c30_TB9661_11 11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 ) . F + 11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 (11ee7bad_7817_372f_ae82_a36163e56c30_TB9661_11. F) using the notations grad , div or curl.A) curl (11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 F) = grad (
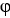 ) . F + 11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 div (F)
) . F + 11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 div (F)B) div (11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 F) = curl (11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 ) . F + 11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 grad (F)
C) div (11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 F) = grad (11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 ) . F + 11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 div (F)
D) grad (11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 F) = div (11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 ) . F + 11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 curl (F)
E) curl (11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 F) = div (11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 ) . F +
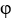 grad (F)
grad (F)
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
36
Every conservative vector field is irrotational.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
37
If r = x i + y j + z k and k is a constant vector field in R3, then
A) div ( k × r) = 0
B) div ( k × r) = 0.
C) grad ( k . r) = 2k
D) curl ( k × r) = 0
E) curl ( k × r) = 0.
A) div ( k × r) = 0
B) div ( k × r) = 0.
C) grad ( k . r) = 2k
D) curl ( k × r) = 0
E) curl ( k × r) = 0.

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
38
Use Green's Theorem to evaluate the line integral 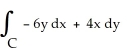 counterclockwise around the square with vertices (0, 3), (3, 0), (-3, 0), and (0, -3).
counterclockwise around the square with vertices (0, 3), (3, 0), (-3, 0), and (0, -3).
A) 18
B) 180
C) -36
D) 0
E) 36
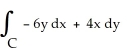 counterclockwise around the square with vertices (0, 3), (3, 0), (-3, 0), and (0, -3).
counterclockwise around the square with vertices (0, 3), (3, 0), (-3, 0), and (0, -3).A) 18
B) 180
C) -36
D) 0
E) 36

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
39
Evaluate the integral 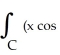 (
( 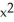 ) - 2y) dx + (3x - ysin(
) - 2y) dx + (3x - ysin( 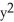 )) dy counterclockwise around the triangle in the xy-plane having vertices (0, 0), (2, 2), and (2, 0).
)) dy counterclockwise around the triangle in the xy-plane having vertices (0, 0), (2, 2), and (2, 0).
A) 5
B) 20
C) 0
D) 10
E) 2
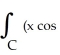 (
( 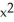 ) - 2y) dx + (3x - ysin(
) - 2y) dx + (3x - ysin( 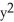 )) dy counterclockwise around the triangle in the xy-plane having vertices (0, 0), (2, 2), and (2, 0).
)) dy counterclockwise around the triangle in the xy-plane having vertices (0, 0), (2, 2), and (2, 0).A) 5
B) 20
C) 0
D) 10
E) 2

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
40
Use Green's Theorem to compute 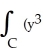 + xy) dx + (
+ xy) dx + ( 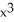 + xy) dy counterclockwise around the rectangle having vertices (± 1, 1) and (± 1, 2).
+ xy) dy counterclockwise around the rectangle having vertices (± 1, 1) and (± 1, 2).
A) -9
B) -12
C) 2
D) 0
E) 12
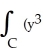 + xy) dx + (
+ xy) dx + ( 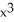 + xy) dy counterclockwise around the rectangle having vertices (± 1, 1) and (± 1, 2).
+ xy) dy counterclockwise around the rectangle having vertices (± 1, 1) and (± 1, 2).A) -9
B) -12
C) 2
D) 0
E) 12

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
41
Use Green's Theorem to compute the integral 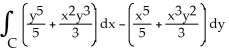 clockwise around the circle of radius 3 centred at the origin.
clockwise around the circle of radius 3 centred at the origin.
A) 18
B) 9
C) 127
D) 243
E) 0
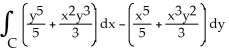 clockwise around the circle of radius 3 centred at the origin.
clockwise around the circle of radius 3 centred at the origin.A) 18
B) 9
C) 127
D) 243
E) 0

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
42
Use Green's Theorem to compute the integral 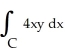 counterclockwise around the square with vertices at (4, 2), (4, 5), (7, 5), and (7, 2).
counterclockwise around the square with vertices at (4, 2), (4, 5), (7, 5), and (7, 2).
A) -198
B) -210
C) -126
D) -72
E) -21
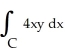 counterclockwise around the square with vertices at (4, 2), (4, 5), (7, 5), and (7, 2).
counterclockwise around the square with vertices at (4, 2), (4, 5), (7, 5), and (7, 2).A) -198
B) -210
C) -126
D) -72
E) -21

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
43
Use Green's Theorem to compute the integral 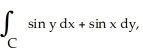 where C is the triangle formed by the lines y = -x + 1, x = 0 and y = 0, oriented clockwise.
where C is the triangle formed by the lines y = -x + 1, x = 0 and y = 0, oriented clockwise.
A) 3
B) 2
C) 1
D) 0
E)
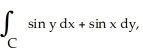 where C is the triangle formed by the lines y = -x + 1, x = 0 and y = 0, oriented clockwise.
where C is the triangle formed by the lines y = -x + 1, x = 0 and y = 0, oriented clockwise.A) 3
B) 2
C) 1
D) 0
E)

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
44
Let C be a non-self-intersecting closed curve in the xy-plane oriented counterclockwise and bounding a region R having area A and centroid 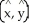 . In terms of these quantities, evaluate the line integral
. In terms of these quantities, evaluate the line integral 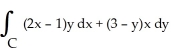 .
.
A) A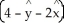
B) A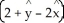
C) A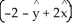
D) A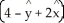
E) -A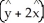
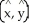 . In terms of these quantities, evaluate the line integral
. In terms of these quantities, evaluate the line integral 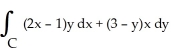 .
.A) A
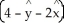
B) A
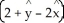
C) A
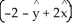
D) A
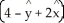
E) -A
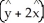

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
45
Evaluate the integral 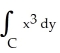 -
- 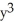 dx counterclockwise around the closed curve formed by y = x3 and y = x, between the points (0, 0) and (1, 1).
dx counterclockwise around the closed curve formed by y = x3 and y = x, between the points (0, 0) and (1, 1).
A) 1
B)
C)
D)
E) 0
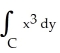 -
- 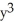 dx counterclockwise around the closed curve formed by y = x3 and y = x, between the points (0, 0) and (1, 1).
dx counterclockwise around the closed curve formed by y = x3 and y = x, between the points (0, 0) and (1, 1).A) 1
B)

C)

D)

E) 0

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
46
Evaluate 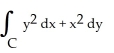 clockwise around the triangle with vertices (0, 0), (3, 0), and (3, 3).
clockwise around the triangle with vertices (0, 0), (3, 0), and (3, 3).
A) 27
B) 9
C) -9
D) -27
E) 0
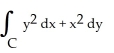 clockwise around the triangle with vertices (0, 0), (3, 0), and (3, 3).
clockwise around the triangle with vertices (0, 0), (3, 0), and (3, 3).A) 27
B) 9
C) -9
D) -27
E) 0

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
47
Let F = - 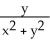 i +
i + 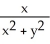 j and let C be the boundary of circle
j and let C be the boundary of circle 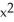 +
+ 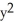 = 9 oriented counterclockwise. Use Green's Theorem to evaluate
= 9 oriented counterclockwise. Use Green's Theorem to evaluate 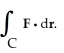
A) 9
B) 0
C) -2
D) 2
E) 3
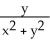 i +
i + 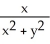 j and let C be the boundary of circle
j and let C be the boundary of circle 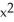 +
+ 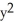 = 9 oriented counterclockwise. Use Green's Theorem to evaluate
= 9 oriented counterclockwise. Use Green's Theorem to evaluate 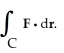
A) 9
B) 0
C) -2
D) 2
E) 3

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
48
Find the flux of F = x i + 2y j out of the circular disk of radius 2 centred at (3, -5).
A) 8
B) 12
C) 16
D) 24
E) 4
A) 8
B) 12
C) 16
D) 24
E) 4

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
49
If C is the positively oriented boundary of a plane region R having area 3 units and centroid at the point (12, 6), evaluate (i) 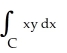 (ii)
(ii) 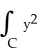 dx + 3xy dy
dx + 3xy dy
A) (i) 36 (ii) 15
B) (i) -36 (ii) 18
C) (i) -18 (ii) 36
D) (i) -4 (ii) 2
E) (i) 432 (ii) 1080
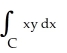 (ii)
(ii) 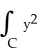 dx + 3xy dy
dx + 3xy dyA) (i) 36 (ii) 15
B) (i) -36 (ii) 18
C) (i) -18 (ii) 36
D) (i) -4 (ii) 2
E) (i) 432 (ii) 1080

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
50
Find the flux of F = 2 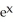 y i +
y i + 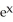
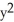 j out of the rectangle 0 x ln(3), 0 y 2.
j out of the rectangle 0 x ln(3), 0 y 2.
A) 4
B) 8
C) 16
D) 32
E) 24
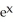 y i +
y i + 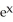
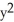 j out of the rectangle 0 x ln(3), 0 y 2.
j out of the rectangle 0 x ln(3), 0 y 2.A) 4
B) 8
C) 16
D) 32
E) 24

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
51
Find the flux of F = 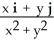 out of (a) the disk
out of (a) the disk 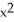 +
+ 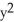
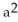 , (b) an arbitrary plane region not containing the origin in its interior or on its boundary, and (c) an arbitrary plane region containing the origin in its interior.
, (b) an arbitrary plane region not containing the origin in its interior or on its boundary, and (c) an arbitrary plane region containing the origin in its interior.
A) (a) 0 (b) 0 (c) 0
B) (a) 2 (b) 0 (c) 2
C) (a) 2 a (b) 0 (c) 2
D) (a) 0 (b) 2 (c) 0
E) None of the above
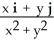 out of (a) the disk
out of (a) the disk 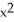 +
+ 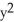
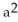 , (b) an arbitrary plane region not containing the origin in its interior or on its boundary, and (c) an arbitrary plane region containing the origin in its interior.
, (b) an arbitrary plane region not containing the origin in its interior or on its boundary, and (c) an arbitrary plane region containing the origin in its interior.A) (a) 0 (b) 0 (c) 0
B) (a) 2 (b) 0 (c) 2
C) (a) 2 a (b) 0 (c) 2
D) (a) 0 (b) 2 (c) 0
E) None of the above

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
52
Use Green's theorem in the plane to show that the area A of a regular plane region R enclosed by a positively oriented, piecewise smooth, simple closed curve C is given by A = 
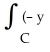 dx + x dy).
dx + x dy).

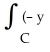 dx + x dy).
dx + x dy).
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
53
Use Green's theorem in the plane to find the x-coordinate of the centroid of a regular plane region R (with areaA) enclosed by a positively oriented, piecewise smooth, simple closed curve C .
A)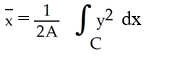
B)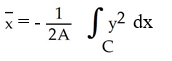
C)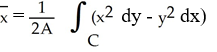
D)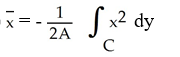
E)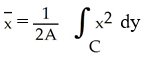
A)
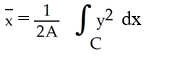
B)
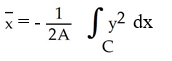
C)
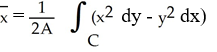
D)
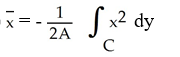
E)
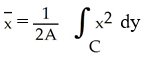

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
54
Use a line integral to find the area enclosed by the x-axis and one arch of the cycloid given parametrically by the equations x(t) = 3(t - sin(t)), y(t) =3(1 - cos(t)), 0 t 2 .
A) 36
B) 18
C) 27
D) 54
E) 9
A) 36
B) 18
C) 27
D) 54
E) 9

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
55
Find the flux of F = x i + 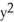 j +
j + 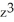 k out of the cube bounded by the coordinate planes and the planes
k out of the cube bounded by the coordinate planes and the planes 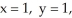 and
and 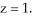
A) 0
B) 1
C)
D) 3
E)
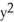 j +
j + 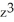 k out of the cube bounded by the coordinate planes and the planes
k out of the cube bounded by the coordinate planes and the planes 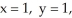 and
and 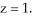
A) 0
B) 1
C)

D) 3
E)


Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
56
Evaluate 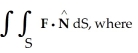 F = x
F = x 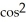 y i + xz j + z
y i + xz j + z 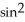 y k and S is the sphere of radius 3 with centre at the origin and unit outward normal field
y k and S is the sphere of radius 3 with centre at the origin and unit outward normal field  .
.
A) 32
B) 34
C) 36
D) 38
E) 72
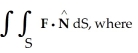 F = x
F = x 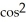 y i + xz j + z
y i + xz j + z 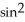 y k and S is the sphere of radius 3 with centre at the origin and unit outward normal field
y k and S is the sphere of radius 3 with centre at the origin and unit outward normal field  .
.A) 32
B) 34
C) 36
D) 38
E) 72

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
57
Evaluate the integral 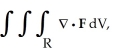 where R is the region
where R is the region 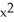 +
+ 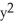 +
+ 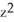 25 and
25 and 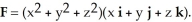
A) 12500
B) 2500
C) 6250
D) 1250
E) 25000
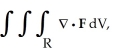 where R is the region
where R is the region 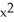 +
+ 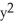 +
+ 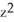 25 and
25 and 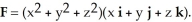
A) 12500
B) 2500
C) 6250
D) 1250
E) 25000

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
58
Use the Divergence Theorem to find the outward flux of F = 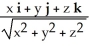 across the boundary of the region
across the boundary of the region 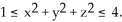
A) 12
B) 16
C) 3
D)
E) 60
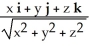 across the boundary of the region
across the boundary of the region 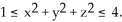
A) 12
B) 16
C) 3
D)
E) 60

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
59
Find the flux of r = x i + y j + z k out of the cone with base 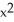 +
+ 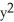 16, z = 0, and vertex at (0, 0, 3).
16, z = 0, and vertex at (0, 0, 3).
A) 46
B) 48
C) 50
D) 52
E) 16
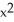 +
+ 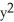 16, z = 0, and vertex at (0, 0, 3).
16, z = 0, and vertex at (0, 0, 3).A) 46
B) 48
C) 50
D) 52
E) 16

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
60
Calculate the surface integral 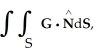 where G = (x + y) i + (y + z) j + (z + x) k and S is the sphere
where G = (x + y) i + (y + z) j + (z + x) k and S is the sphere 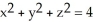 with outward normal.
with outward normal.
A) 32
B) 16
C) 8
D) 64
E) 256
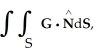 where G = (x + y) i + (y + z) j + (z + x) k and S is the sphere
where G = (x + y) i + (y + z) j + (z + x) k and S is the sphere 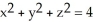 with outward normal.
with outward normal.A) 32
B) 16
C) 8
D) 64
E) 256

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
61
Find the flux of 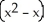 i - xy j +3z k out of the solid region bounded by the parabolic cylinder
i - xy j +3z k out of the solid region bounded by the parabolic cylinder 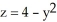 and the planes
and the planes 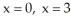 , and
, and 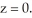
A) 208
B) 112
C) 64
D) 48
E) 176
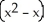 i - xy j +3z k out of the solid region bounded by the parabolic cylinder
i - xy j +3z k out of the solid region bounded by the parabolic cylinder 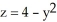 and the planes
and the planes 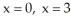 , and
, and 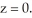
A) 208
B) 112
C) 64
D) 48
E) 176

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
62
Evaluate 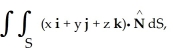 where S is the first-octant part of the sphere of radius a centred at the origin. (Hint: Even though S is not a closed surface, it is still easiest to use the Divergence Theorem because the integrand in the surface integral is zero on the coordinate planes.)
where S is the first-octant part of the sphere of radius a centred at the origin. (Hint: Even though S is not a closed surface, it is still easiest to use the Divergence Theorem because the integrand in the surface integral is zero on the coordinate planes.)
A)
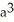
B)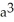
C)
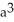
D) 2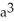
E)
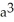
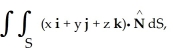 where S is the first-octant part of the sphere of radius a centred at the origin. (Hint: Even though S is not a closed surface, it is still easiest to use the Divergence Theorem because the integrand in the surface integral is zero on the coordinate planes.)
where S is the first-octant part of the sphere of radius a centred at the origin. (Hint: Even though S is not a closed surface, it is still easiest to use the Divergence Theorem because the integrand in the surface integral is zero on the coordinate planes.)A)

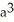
B)
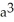
C)

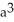
D) 2
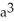
E)

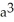

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
63
Let C be a cone whose base is an arbitrarily shaped region in the plane z = h > 0 having area A, and whose vertex is at the origin. By calculating the flux of 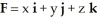 out of C through its entire surface both directly and by using the Divergence Theorem, find the volume of C.
out of C through its entire surface both directly and by using the Divergence Theorem, find the volume of C.
A) Ah
Ah
B)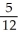 Ah
Ah
C) Ah
Ah
D) Ah
Ah
E) 3 Ah
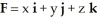 out of C through its entire surface both directly and by using the Divergence Theorem, find the volume of C.
out of C through its entire surface both directly and by using the Divergence Theorem, find the volume of C.A)
 Ah
AhB)
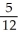 Ah
AhC)
 Ah
AhD)
 Ah
AhE) 3 Ah

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
64
Evaluate the surface integral 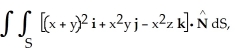 where
where  is the unit inner normal to the surface S of the region lying between the two paraboloids
is the unit inner normal to the surface S of the region lying between the two paraboloids 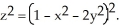
A)
B) 1
C) 0
D) 2
E) -1
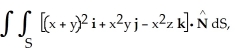 where
where  is the unit inner normal to the surface S of the region lying between the two paraboloids
is the unit inner normal to the surface S of the region lying between the two paraboloids 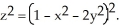
A)

B) 1
C) 0
D) 2
E) -1

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
65
Find the flux of G = (x 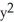 + 2zy) i + (y
+ 2zy) i + (y 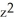 -
- 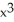 ) j +
) j + 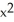 z k outward through the sphere
z k outward through the sphere 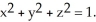
A)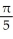
B)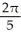
C)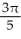
D)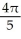
E)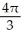
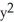 + 2zy) i + (y
+ 2zy) i + (y 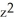 -
- 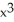 ) j +
) j + 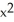 z k outward through the sphere
z k outward through the sphere 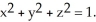
A)
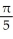
B)
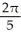
C)
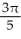
D)
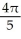
E)
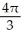

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
66
Use the Divergence Theorem to evaluate the surface integral 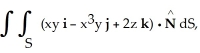 where S is the part of the cone
where S is the part of the cone 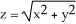 below z = 2, and
below z = 2, and  is the unit normal to S with positive z-component. (An additional surface must be introduced to enclose a volume.)
is the unit normal to S with positive z-component. (An additional surface must be introduced to enclose a volume.)
A)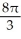
B)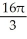
C)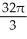
D)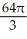
E)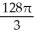
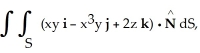 where S is the part of the cone
where S is the part of the cone 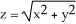 below z = 2, and
below z = 2, and  is the unit normal to S with positive z-component. (An additional surface must be introduced to enclose a volume.)
is the unit normal to S with positive z-component. (An additional surface must be introduced to enclose a volume.)A)
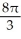
B)
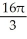
C)
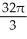
D)
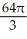
E)
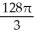

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
67
If F = x i + y j, calculate the flux of F upward through the part of the surface z = 4 - x2 - y2 that lies above the (x, y) plane by applying the Divergence Theorem to the volume bounded by the surface and the disk that it cuts out of the (x, y) plane.
A) 14
B) 16
C) 18
D) 20
E) 8
A) 14
B) 16
C) 18
D) 20
E) 8

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
68
Find the outward flux of F = ln( 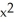 +
+ 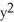 ) i -
) i - 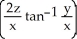 j + z
j + z 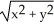 k across the boundary of the region
k across the boundary of the region 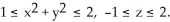
A) 4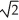 - 3 ln 2 + 2
- 3 ln 2 + 2
B) 4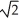 - 3 ln 2 - 2
- 3 ln 2 - 2
C) 4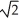 + 3 ln 2 - 2
+ 3 ln 2 - 2
D) 4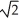 + 3 ln 2 + 2
+ 3 ln 2 + 2
E) 4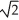 +
+  ln 2 - 2
ln 2 - 2
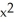 +
+ 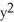 ) i -
) i - 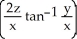 j + z
j + z 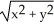 k across the boundary of the region
k across the boundary of the region 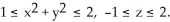
A) 4
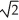 - 3 ln 2 + 2
- 3 ln 2 + 2 B) 4
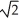 - 3 ln 2 - 2
- 3 ln 2 - 2 C) 4
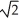 + 3 ln 2 - 2
+ 3 ln 2 - 2 D) 4
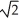 + 3 ln 2 + 2
+ 3 ln 2 + 2 E) 4
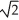 +
+  ln 2 - 2
ln 2 - 2 
Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
69
A certain region R in 3-space has volume 5 cubic units and centroid at the point (2, -3, 4). Find the flux of 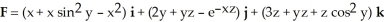 out of R across its boundary.
out of R across its boundary.
A) 60
B) 50
C) 20
D) 15
E) 90
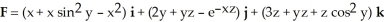 out of R across its boundary.
out of R across its boundary.A) 60
B) 50
C) 20
D) 15
E) 90

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
70
Find 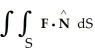 , where F(x, y, z) = x
, where F(x, y, z) = x 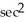 y i +
y i + 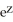 ln x j - z
ln x j - z 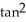 y k, S is the sphere of radius 3 centred at the origin, and
y k, S is the sphere of radius 3 centred at the origin, and  is the unit outward normal field on S.
is the unit outward normal field on S.
A) 24
B) 12
C) 36
D) 72
E) 54
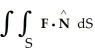 , where F(x, y, z) = x
, where F(x, y, z) = x 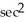 y i +
y i + 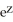 ln x j - z
ln x j - z 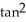 y k, S is the sphere of radius 3 centred at the origin, and
y k, S is the sphere of radius 3 centred at the origin, and  is the unit outward normal field on S.
is the unit outward normal field on S.A) 24
B) 12
C) 36
D) 72
E) 54

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
71
Given F = 4y i + x j + 2z k, find 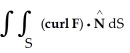 over the hemisphere
over the hemisphere 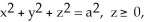 with outward normal
with outward normal  .
.
A) 2
B) -2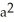
C) -3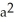
D) 3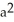
E) 0
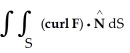 over the hemisphere
over the hemisphere 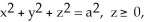 with outward normal
with outward normal  .
.A) 2
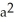
B) -2
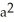
C) -3
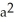
D) 3
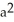
E) 0

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
72
Evaluate the integral of 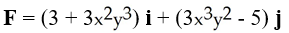 over the portion of the ellipse
over the portion of the ellipse 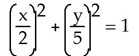 in the first quadrant, traversed in the counterclockwise direction.
in the first quadrant, traversed in the counterclockwise direction.
A) -31
B) -32
C) -33
D) -34
E) -30
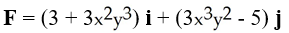 over the portion of the ellipse
over the portion of the ellipse 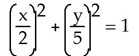 in the first quadrant, traversed in the counterclockwise direction.
in the first quadrant, traversed in the counterclockwise direction. A) -31
B) -32
C) -33
D) -34
E) -30

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
73
Use Stokes's Theorem to evaluate the line integral 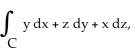 where C is the triangle with vertices (0, 0, 1), (0, 1, 1) and (1, 0, 0) with counterclockwise orientation as seen from high on the z-axis.
where C is the triangle with vertices (0, 0, 1), (0, 1, 1) and (1, 0, 0) with counterclockwise orientation as seen from high on the z-axis.
A) 0
B) 1
C) -1
D) 2
E) -2
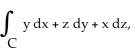 where C is the triangle with vertices (0, 0, 1), (0, 1, 1) and (1, 0, 0) with counterclockwise orientation as seen from high on the z-axis.
where C is the triangle with vertices (0, 0, 1), (0, 1, 1) and (1, 0, 0) with counterclockwise orientation as seen from high on the z-axis.A) 0
B) 1
C) -1
D) 2
E) -2

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
74
Let F be a smooth vector field in 3-space satisfying the condition 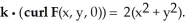 Find the flux of curl F upward through the part of the
Find the flux of curl F upward through the part of the 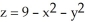 lying above the xy-plane.
lying above the xy-plane.
A) 81
B) 72
C) 27
D) 18
E) None of the above
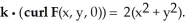 Find the flux of curl F upward through the part of the
Find the flux of curl F upward through the part of the 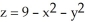 lying above the xy-plane.
lying above the xy-plane.A) 81
B) 72
C) 27
D) 18
E) None of the above

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
75
Evaluate the line integral 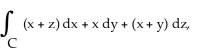 where C is the circle given by the parametric equations
where C is the circle given by the parametric equations 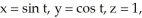 for
for 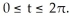
A) -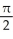
B) -
C)
D) 2
E)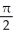
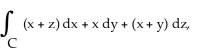 where C is the circle given by the parametric equations
where C is the circle given by the parametric equations 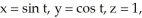 for
for 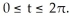
A) -
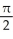
B) -
C)
D) 2
E)
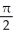

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
76
Evaluate the line integral 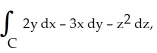 where C is the circle
where C is the circle 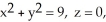 oriented clockwise as seen from high on the z-axis.
oriented clockwise as seen from high on the z-axis.
A) 40
B) 45
C) 50
D) 55
E) 35
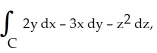 where C is the circle
where C is the circle 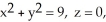 oriented clockwise as seen from high on the z-axis.
oriented clockwise as seen from high on the z-axis.A) 40
B) 45
C) 50
D) 55
E) 35

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
77
Evaluate 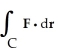 , where F = y i + zx j +
, where F = y i + zx j + 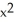 k and C are the positively oriented boundary of the triangle in which the plane
k and C are the positively oriented boundary of the triangle in which the plane 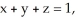 with upward normal, intersects the first octant of space.
with upward normal, intersects the first octant of space.
A)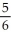
B) -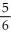
C)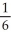
D) -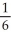
E) -
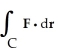 , where F = y i + zx j +
, where F = y i + zx j + 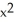 k and C are the positively oriented boundary of the triangle in which the plane
k and C are the positively oriented boundary of the triangle in which the plane 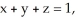 with upward normal, intersects the first octant of space.
with upward normal, intersects the first octant of space.A)
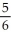
B) -
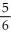
C)
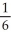
D) -
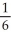
E) -


Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
78
Use Stokes's Theorem to evaluate the line integral 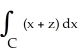 + (2x - y) dy + (y + z) dz,where C is the triangle cut from the plane P with equation
+ (2x - y) dy + (y + z) dz,where C is the triangle cut from the plane P with equation 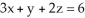 by the three coordinate planes. C has orientation inherited from the upward normal on P.
by the three coordinate planes. C has orientation inherited from the upward normal on P.
A) 18
B) -6
C) 6
D) 24
E) -24
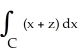 + (2x - y) dy + (y + z) dz,where C is the triangle cut from the plane P with equation
+ (2x - y) dy + (y + z) dz,where C is the triangle cut from the plane P with equation 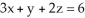 by the three coordinate planes. C has orientation inherited from the upward normal on P.
by the three coordinate planes. C has orientation inherited from the upward normal on P.A) 18
B) -6
C) 6
D) 24
E) -24

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
79
Use Stokes's Theorem to evaluate the line integral 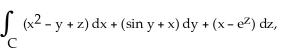 where C is the triangle with vertices (1, 1, 1), (0, 1, 0) and (0, 0, 0) oriented counterclockwise as seen from high on the z-axis.
where C is the triangle with vertices (1, 1, 1), (0, 1, 0) and (0, 0, 0) oriented counterclockwise as seen from high on the z-axis.
A) 0
B) 1
C) 2
D) -2
E) -1
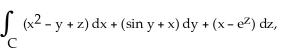 where C is the triangle with vertices (1, 1, 1), (0, 1, 0) and (0, 0, 0) oriented counterclockwise as seen from high on the z-axis.
where C is the triangle with vertices (1, 1, 1), (0, 1, 0) and (0, 0, 0) oriented counterclockwise as seen from high on the z-axis.A) 0
B) 1
C) 2
D) -2
E) -1

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck
80
Let F = (z - y) i + (x - z) j + (y - x) k. Compute the work done by the force F in moving an object along the curve of intersection of the cylinder 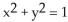 with the plane
with the plane 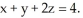 The orientation of the curve is consistent with the upward normal on the plane.
The orientation of the curve is consistent with the upward normal on the plane.
A) 8
B) 6
C) 4
D) 2
E) 0
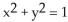 with the plane
with the plane 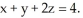 The orientation of the curve is consistent with the upward normal on the plane.
The orientation of the curve is consistent with the upward normal on the plane.A) 8
B) 6
C) 4
D) 2
E) 0

Unlock Deck
Unlock for access to all 92 flashcards in this deck.
Unlock Deck
k this deck


