Exam 17: Vector Calculus
Exam 1: Preliminaries127 Questions
Exam 2: Limits and Continuity92 Questions
Exam 3: Differentiation131 Questions
Exam 4: Transcendental Functions129 Questions
Exam 5: More Applications of Differentiation130 Questions
Exam 6: Integration117 Questions
Exam 7: Techniques of Integration118 Questions
Exam 8: Applications of Integration139 Questions
Exam 9: Conics, Parametric Curves, and Polar Curves114 Questions
Exam 10: Sequences, Series, and Power Series125 Questions
Exam 11: Vectors and Coordinate Geometry in 3-Space119 Questions
Exam 12: Vector Functions and Curves87 Questions
Exam 13: Partial Differentiation104 Questions
Exam 14: Applications of Partial Derivatives67 Questions
Exam 15: Multiple Integration105 Questions
Exam 16: Vector Fields90 Questions
Exam 17: Vector Calculus92 Questions
Exam 18: Differential Forms and Exterior Calculus76 Questions
Exam 19: Ordinary Differential Equations135 Questions
Select questions type
Evaluate 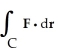 , where F = y i + zx j +
, where F = y i + zx j + 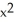 k and C are the positively oriented boundary of the triangle in which the plane
k and C are the positively oriented boundary of the triangle in which the plane 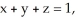 with upward normal, intersects the first octant of space.
with upward normal, intersects the first octant of space.
Free
(Multiple Choice)
4.9/5  (33)
(33)
Correct Answer:
B
Every conservative vector field is irrotational.
Free
(True/False)
4.8/5  (35)
(35)
Correct Answer:
True
Find the flux of F = 2 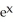 y i +
y i + 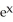
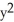 j out of the rectangle 0 x ln(3), 0 y 2.
j out of the rectangle 0 x ln(3), 0 y 2.
Free
(Multiple Choice)
4.9/5  (33)
(33)
Correct Answer:
C
A vector field F satisfying the equation div F = 0 in domain D is called:
(Multiple Choice)
4.8/5  (39)
(39)
For what value of the constant C is the vector field F = 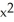 i + C(xy + yz) j +
i + C(xy + yz) j + 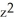 k. solenoidal?
If C has that value, find a vector potential G for F having the form G(x, y, z) =
k. solenoidal?
If C has that value, find a vector potential G for F having the form G(x, y, z) = 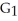 (x, y, z) i +
(x, y, z) i + 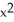 y k.
y k.
(Multiple Choice)
4.9/5  (30)
(30)
 . F = F . 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 for any sufficiently smooth vector field F.
. F = F . 11ee7bac_9657_298c_ae82_2b2223aa180c_TB9661_11 for any sufficiently smooth vector field F.
(True/False)
4.8/5  (33)
(33)
Show that div ( 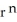 r) = (n + 3)
r) = (n + 3) 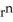 .You may use the following fact: grad (
.You may use the following fact: grad ( 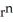 ) = n
) = n 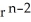 r
r
(Essay)
4.8/5  (29)
(29)
Use Green's Theorem to compute the integral 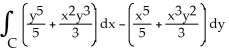 clockwise around the circle of radius 3 centred at the origin.
clockwise around the circle of radius 3 centred at the origin.
(Multiple Choice)
4.8/5  (37)
(37)
Compute the gradient of the function f(x, y) = 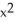 sin y +
sin y + 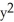 cos x.
cos x.
(Multiple Choice)
4.8/5  (35)
(35)
Find the flux of F = 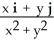 out of (a) the disk
out of (a) the disk 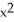 +
+ 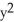
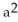 , (b) an arbitrary plane region not containing the origin in its interior or on its boundary, and (c) an arbitrary plane region containing the origin in its interior.
, (b) an arbitrary plane region not containing the origin in its interior or on its boundary, and (c) an arbitrary plane region containing the origin in its interior.
(Multiple Choice)
4.9/5  (22)
(22)
If F = x i + y j, calculate the flux of F upward through the part of the surface z = 4 - x2 - y2 that lies above the (x, y) plane by applying the Divergence Theorem to the volume bounded by the surface and the disk that it cuts out of the (x, y) plane.
(Multiple Choice)
4.8/5  (33)
(33)
Verify that the vector field F = (2x y2z2 - sin(x)sin(y)) i + (2 x2y z2+ cos(x)cos(y)) j + (2x2y2 z + ) k is conservative and find a scalar potential f(x, y, z) for it that satisfies f(0, 0, 0) = 1.
(Multiple Choice)
4.8/5  (35)
(35)
Compute div F for F = (2x + yz) i + ( 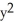 +
+ 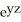 ) j + (x sin(z) +
) j + (x sin(z) + 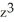 ) k.
) k.
(Multiple Choice)
4.8/5  (41)
(41)
If r = x i + y j + z k and f(u) is any differentiable function of one variable, evaluate and simplify 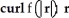 .
.
(Multiple Choice)
4.7/5  (38)
(38)
Evaluate 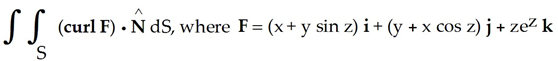 and S is the part of the sphere
and S is the part of the sphere 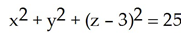 that lies above the xy-plane with outward normal field.
that lies above the xy-plane with outward normal field.
(Multiple Choice)
4.9/5  (40)
(40)
Use Stokes's Theorem to evaluate the line integral 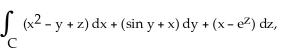 where C is the triangle with vertices (1, 1, 1), (0, 1, 0) and (0, 0, 0) oriented counterclockwise as seen from high on the z-axis.
where C is the triangle with vertices (1, 1, 1), (0, 1, 0) and (0, 0, 0) oriented counterclockwise as seen from high on the z-axis.
(Multiple Choice)
4.9/5  (28)
(28)
Calculate the divergence of the vector field F(x, y, z) = ( 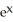 - xz) i + (z
- xz) i + (z 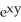 -
- 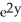 ) j - xy
) j - xy 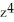 k.
k.
(Multiple Choice)
4.9/5  (37)
(37)
Use a line integral to find the area enclosed by the x-axis and one arch of the cycloid given parametrically by the equations x(t) = 3(t - sin(t)), y(t) =3(1 - cos(t)), 0 t 2 .
(Multiple Choice)
4.9/5  (41)
(41)
Use Stokes's Theorem to evaluate the line integral 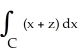 + (2x - y) dy + (y + z) dz,where C is the triangle cut from the plane P with equation
+ (2x - y) dy + (y + z) dz,where C is the triangle cut from the plane P with equation 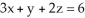 by the three coordinate planes. C has orientation inherited from the upward normal on P.
by the three coordinate planes. C has orientation inherited from the upward normal on P.
(Multiple Choice)
4.7/5  (40)
(40)
Verify that the vector field F = 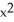 i + (1 - xy) j - xz k is solenoidal, and find a vector potential G for it having the form G(x, y, z) =
i + (1 - xy) j - xz k is solenoidal, and find a vector potential G for it having the form G(x, y, z) =  (x, y, z) i +
(x, y, z) i + 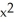 y k.
y k.
(Multiple Choice)
4.9/5  (34)
(34)
Showing 1 - 20 of 92
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)