Deck 16: Vector Fields
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/90
Play
Full screen (f)
Deck 16: Vector Fields
1
Find the gradient vector field of f(x, y) = ln ( 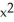 + 3y).
+ 3y).
A)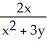 i +
i + 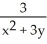 j
j
B)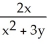 i +
i + 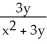 j
j
C)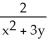 i +
i + 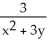 j
j
D)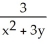 i +
i + 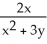 j
j
E)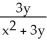 i +
i + 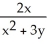 j
j
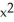 + 3y).
+ 3y).A)
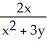 i +
i + 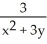 j
jB)
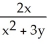 i +
i + 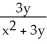 j
jC)
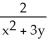 i +
i + 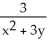 j
jD)
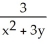 i +
i + 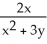 j
jE)
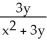 i +
i + 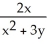 j
j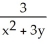 i +
i + 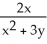 j
j 2
Find the gradient vector field  f(x,y) of f(x, y) =
f(x,y) of f(x, y) = 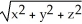 .
.
A) -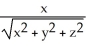 i -
i - 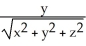 j -
j - 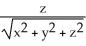 k
k
B)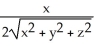 i +
i + 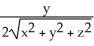 j +
j + 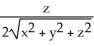 k
k
C)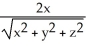 i +
i + 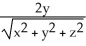 j +
j + 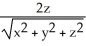 k
k
D)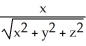 i +
i + 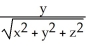 j +
j + 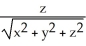 k
k
E) -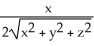 i -
i - 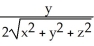 j -
j - 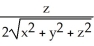 k
k
 f(x,y) of f(x, y) =
f(x,y) of f(x, y) = 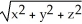 .
.A) -
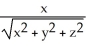 i -
i - 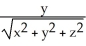 j -
j - 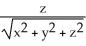 k
kB)
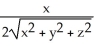 i +
i + 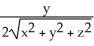 j +
j + 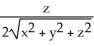 k
kC)
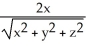 i +
i + 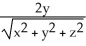 j +
j + 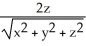 k
kD)
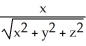 i +
i + 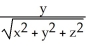 j +
j + 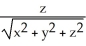 k
kE) -
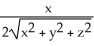 i -
i - 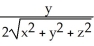 j -
j - 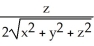 k
k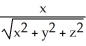 i +
i + 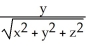 j +
j + 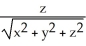 k
k 3
Describe the streamlines of the given velocity field v(x, y, z) = - yi + xj.
A) concentric circles centred on the x-axis in planes perpendicular to the x-axis
B) concentric circles centred on the y-axis in planes perpendicular to the y-axis
C) concentric circles centred on the z-axis in planes perpendicular to the z-axis
D) hyperbolas in planes perpendicular to the z-axis
E) parabolas in planes perpendicular to the z-axis
A) concentric circles centred on the x-axis in planes perpendicular to the x-axis
B) concentric circles centred on the y-axis in planes perpendicular to the y-axis
C) concentric circles centred on the z-axis in planes perpendicular to the z-axis
D) hyperbolas in planes perpendicular to the z-axis
E) parabolas in planes perpendicular to the z-axis
concentric circles centred on the z-axis in planes perpendicular to the z-axis
4
Show that r(t) =  i + 2t j +
i + 2t j + 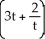 k for t ≠ 0 is a streamline for the velocity vector field
k for t ≠ 0 is a streamline for the velocity vector field 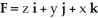 .
.
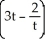 i + 2t j +
i + 2t j + 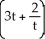 k for t ≠ 0 is a streamline for the velocity vector field
k for t ≠ 0 is a streamline for the velocity vector field 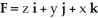 .
.
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
5
Find the family of field lines of the plane polar field F(r, ) = 2  +
+  .
.
A) r = C
B) r =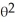 + C
+ C
C) r = C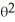
D) r = C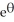
E) r = ln
 +
+  .
.A) r = C
B) r =
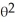 + C
+ CC) r = C
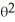
D) r = C
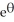
E) r = ln

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
6
Find parametric equations of the streamline of the velocity field v(x, y, z) = y i - y j + y k that passes through the point (2, -3, -4).
A) x = 2 + t, y = -3 - t, z = -4 + t
B) x = 2 + t, y = -3 + t, z = -4 + t
C) x = 2 + t, y = -3 - t, z = -4 - t
D) x = 2 + t, y = 3 - t, z = 4 + t
E) x = 2t, y = -3t, z = -4t
A) x = 2 + t, y = -3 - t, z = -4 + t
B) x = 2 + t, y = -3 + t, z = -4 + t
C) x = 2 + t, y = -3 - t, z = -4 - t
D) x = 2 + t, y = 3 - t, z = 4 + t
E) x = 2t, y = -3t, z = -4t

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
7
Find a vector parametric equation of the field line of the vector field F(x, y, z) = -y i + x j + k that passes through the point (2, 0, 0).
A) r = 2 cos t i + 2 sin t j - t k
B) r = 2 cos t i + 2 sin t j + t k
C) r = 2 cos t i - 2 sin t j + t k
D) r = cos t i + sin t j + t k
E) r = 2 cos t i + 2 sin t j
A) r = 2 cos t i + 2 sin t j - t k
B) r = 2 cos t i + 2 sin t j + t k
C) r = 2 cos t i - 2 sin t j + t k
D) r = cos t i + sin t j + t k
E) r = 2 cos t i + 2 sin t j

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
8
Define carefully what is meant by: The function V(x,y) is a Liapunov function in a domain D (containing the fixed point at the origin) for the autonomous system associated with the vector field F = P(x,y) i + Q(j, x,y).Assume that P and Q have continuous partial derivatives in D.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
9
The function V(x,y) = 3 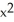 +3xy + 5
+3xy + 5  is a Liapunov function for the autonomous system associated with the vector field F = (y -7x) i + (3x - 5y) j in any domain D containing the fixed point at the origin.
is a Liapunov function for the autonomous system associated with the vector field F = (y -7x) i + (3x - 5y) j in any domain D containing the fixed point at the origin.
 +3xy + 5
+3xy + 5  is a Liapunov function for the autonomous system associated with the vector field F = (y -7x) i + (3x - 5y) j in any domain D containing the fixed point at the origin.
is a Liapunov function for the autonomous system associated with the vector field F = (y -7x) i + (3x - 5y) j in any domain D containing the fixed point at the origin.
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
10
Use a suitable Liapunov function to show that the fixed point at the origin for the autonomous system 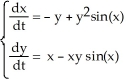 is at least stable.
is at least stable.
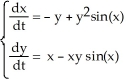 is at least stable.
is at least stable.
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
11
Use the Liapunov function V(x,y) =  (
( 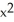 +
+ 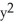 ) to determine the stability of the fixed point at the origin of an autonomous system associated with the vector field F = (- y - x
) to determine the stability of the fixed point at the origin of an autonomous system associated with the vector field F = (- y - x 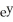 ) i + (x - y
) i + (x - y 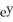 ) j.
) j.
 (
( 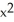 +
+ 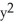 ) to determine the stability of the fixed point at the origin of an autonomous system associated with the vector field F = (- y - x
) to determine the stability of the fixed point at the origin of an autonomous system associated with the vector field F = (- y - x 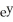 ) i + (x - y
) i + (x - y 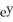 ) j.
) j.
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
12
Show that the fixed point at the origin for the autonomous system 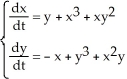 is unstable.
is unstable.
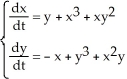 is unstable.
is unstable.
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
13
The Liapunov function V(x,y) = 2 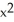 - xy + 3
- xy + 3 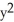 is suitable to confirm that the fixed point at the origin for the autonomous system
is suitable to confirm that the fixed point at the origin for the autonomous system 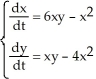 is at least stable.
is at least stable.
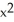 - xy + 3
- xy + 3 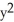 is suitable to confirm that the fixed point at the origin for the autonomous system
is suitable to confirm that the fixed point at the origin for the autonomous system 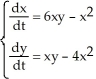 is at least stable.
is at least stable.
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
14
Let V(x , y) = A 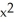 + B
+ B 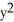 , where A and B are constant real numbers, be a Liapunov function in a domain D (containing the fixed point at the origin) for the autonomous non-linear system
, where A and B are constant real numbers, be a Liapunov function in a domain D (containing the fixed point at the origin) for the autonomous non-linear system 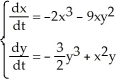 .Find A and B if the derivative of V along the trajectories of the system is equal to -
.Find A and B if the derivative of V along the trajectories of the system is equal to - 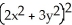 .Is the origin stable, asymptotically stable, or unstable?
.Is the origin stable, asymptotically stable, or unstable?
A) A = 2, B = -3; asymptotically stable
B) A = -2, B = -3; unstable
C) A =2, B = 3; unstable
D) A = -2, B = 3; stable
E) A = 2, B = 3; asymptotically stable
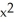 + B
+ B 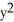 , where A and B are constant real numbers, be a Liapunov function in a domain D (containing the fixed point at the origin) for the autonomous non-linear system
, where A and B are constant real numbers, be a Liapunov function in a domain D (containing the fixed point at the origin) for the autonomous non-linear system 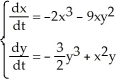 .Find A and B if the derivative of V along the trajectories of the system is equal to -
.Find A and B if the derivative of V along the trajectories of the system is equal to - 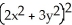 .Is the origin stable, asymptotically stable, or unstable?
.Is the origin stable, asymptotically stable, or unstable?A) A = 2, B = -3; asymptotically stable
B) A = -2, B = -3; unstable
C) A =2, B = 3; unstable
D) A = -2, B = 3; stable
E) A = 2, B = 3; asymptotically stable

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
15
Is F (x,y) = (3 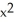 y + 2x
y + 2x 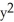 + 1) i + (
+ 1) i + ( 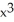 + 2
+ 2 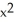 y + 1) j conservative? If so, find a potential for it.
y + 1) j conservative? If so, find a potential for it.
A)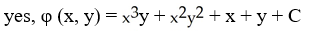
B)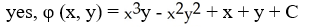
C)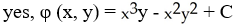
D)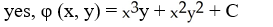
E) No, it is not conservative.
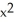 y + 2x
y + 2x 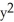 + 1) i + (
+ 1) i + ( 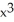 + 2
+ 2 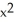 y + 1) j conservative? If so, find a potential for it.
y + 1) j conservative? If so, find a potential for it.A)
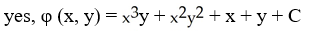
B)
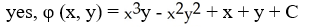
C)
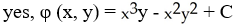
D)
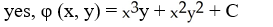
E) No, it is not conservative.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
16
Is F (x,y,z) = 6xy sin(2z) i + 3 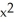 sin(2z) j - 6 xy cos(2z) k conservative? If so, find a potential for it.
sin(2z) j - 6 xy cos(2z) k conservative? If so, find a potential for it.
A) yes,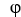 (x,y) = 3
(x,y) = 3 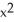 y sin(2z) + C
y sin(2z) + C
B) yes, 11ee7ba1_26b3_e973_ae82_2f72847b9867_TB9661_11 (x,y) = 3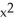 y cos(2z) + C
y cos(2z) + C
C) yes, 11ee7ba1_26b3_e973_ae82_2f72847b9867_TB9661_11 (x,y) = 6xy sin(2z) + C
D) yes, 11ee7ba1_26b3_e973_ae82_2f72847b9867_TB9661_11 (x,y) = 3x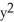 sin(2z) + C
sin(2z) + C
E) No, it is not conservative.
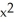 sin(2z) j - 6 xy cos(2z) k conservative? If so, find a potential for it.
sin(2z) j - 6 xy cos(2z) k conservative? If so, find a potential for it.A) yes,
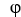 (x,y) = 3
(x,y) = 3 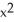 y sin(2z) + C
y sin(2z) + CB) yes, 11ee7ba1_26b3_e973_ae82_2f72847b9867_TB9661_11 (x,y) = 3
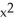 y cos(2z) + C
y cos(2z) + CC) yes, 11ee7ba1_26b3_e973_ae82_2f72847b9867_TB9661_11 (x,y) = 6xy sin(2z) + C
D) yes, 11ee7ba1_26b3_e973_ae82_2f72847b9867_TB9661_11 (x,y) = 3x
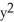 sin(2z) + C
sin(2z) + CE) No, it is not conservative.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
17
An equipotential surface of a conservative vector field F is given by 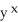 + ln(
+ ln( 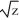 ) = 12 for y, z > 0.Find F.
) = 12 for y, z > 0.Find F.
A)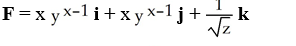
B)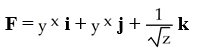
C)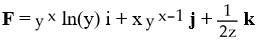
D)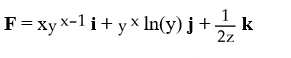
E)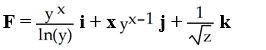
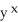 + ln(
+ ln( 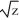 ) = 12 for y, z > 0.Find F.
) = 12 for y, z > 0.Find F.A)
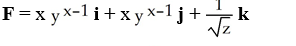
B)
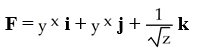
C)
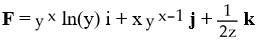
D)
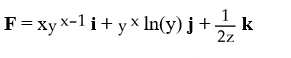
E)
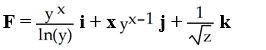

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
18
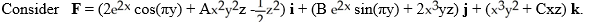 For what values of the constants A, B, and C is F conservative?
For what values of the constants A, B, and C is F conservative?A) A = 2, B = - , C = 1
B) A = 3, B = - , C = -1
C) A = 3, B = -2, C = -1
D) A = 2, B = , C = 2
E) There are no values of A, B, and C that will make F conservative.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
19
The gradient of a scalar field ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee7ba9_d077_68d8_ae82_6357d8c80115_TB9661_11.jpg) expressed in terms of polar coordinates [r, ] in the plane is
expressed in terms of polar coordinates [r, ] in the plane is![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee7ba1_8550_5724_ae82_1fed9cde7479_TB9661_11.jpg) (r, ) =
(r, ) = ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de41_a0f8_0f3ea7ccd08b_TB9661_11.jpg)
![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de42_a0f8_2fd44569cc80_TB9661_11.jpg) +
+ ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de43_a0f8_61d586b44d12_TB9661_11.jpg) .
. ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de44_a0f8_b346e40bf9b3_TB9661_11.jpg)
![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de45_a0f8_93245f5dc084_TB9661_11.jpg) Use the result above to find the necessary condition for the vector field F(r, ) = P(r, )
Use the result above to find the necessary condition for the vector field F(r, ) = P(r, ) ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de46_a0f8_0766653367fc_TB9661_11.jpg) + Q(r, )
+ Q(r, ) ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de47_a0f8_01b43d2ef1f7_TB9661_11.jpg) to be conservative.
to be conservative.
A)![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de48_a0f8_f3caef633b0e_TB9661_11.jpg) =
= ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de49_a0f8_734863b5ae26_TB9661_11.jpg)
B)![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de4a_a0f8_87af9f342c20_TB9661_11.jpg) = r
= r ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de4b_a0f8_1f6a31408a7b_TB9661_11.jpg)
C)![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de4c_a0f8_dd3e1f2df27b_TB9661_11.jpg) = -
= - ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de4d_a0f8_19f3022176de_TB9661_11.jpg)
![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de4e_a0f8_61457bb16978_TB9661_11.jpg)
D)![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de4f_a0f8_2744ec5270f7_TB9661_11.jpg) - r
- r ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de50_a0f8_27651820fed5_TB9661_11.jpg) = Q
= Q
E)![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de51_a0f8_ad18cb9aae80_TB9661_11.jpg) -
- ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de52_a0f8_cbc3d949ab1c_TB9661_11.jpg) = r
= r
![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee7ba9_d077_68d8_ae82_6357d8c80115_TB9661_11.jpg) expressed in terms of polar coordinates [r, ] in the plane is
expressed in terms of polar coordinates [r, ] in the plane is![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee7ba1_8550_5724_ae82_1fed9cde7479_TB9661_11.jpg) (r, ) =
(r, ) = ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de41_a0f8_0f3ea7ccd08b_TB9661_11.jpg)
![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de42_a0f8_2fd44569cc80_TB9661_11.jpg) +
+ ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de43_a0f8_61d586b44d12_TB9661_11.jpg) .
. ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de44_a0f8_b346e40bf9b3_TB9661_11.jpg)
![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de45_a0f8_93245f5dc084_TB9661_11.jpg) Use the result above to find the necessary condition for the vector field F(r, ) = P(r, )
Use the result above to find the necessary condition for the vector field F(r, ) = P(r, ) ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de46_a0f8_0766653367fc_TB9661_11.jpg) + Q(r, )
+ Q(r, ) ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de47_a0f8_01b43d2ef1f7_TB9661_11.jpg) to be conservative.
to be conservative.A)
![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de48_a0f8_f3caef633b0e_TB9661_11.jpg) =
= ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de49_a0f8_734863b5ae26_TB9661_11.jpg)
B)
![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de4a_a0f8_87af9f342c20_TB9661_11.jpg) = r
= r ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de4b_a0f8_1f6a31408a7b_TB9661_11.jpg)
C)
![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de4c_a0f8_dd3e1f2df27b_TB9661_11.jpg) = -
= - ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de4d_a0f8_19f3022176de_TB9661_11.jpg)
![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de4e_a0f8_61457bb16978_TB9661_11.jpg)
D)
![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de4f_a0f8_2744ec5270f7_TB9661_11.jpg) - r
- r ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de50_a0f8_27651820fed5_TB9661_11.jpg) = Q
= QE)
![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de51_a0f8_ad18cb9aae80_TB9661_11.jpg) -
- ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the necessary condition for the vector field F(r, \theta ) = P(r, \theta ) + Q(r, \theta ) to be conservative.</strong> A) = B) = r C) = - D) - r = Q E) - = r](https://storage.examlex.com/TB9661/11ee77e1_779c_de52_a0f8_cbc3d949ab1c_TB9661_11.jpg) = r
= r
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
20
Find the equipotential surfaces of the conservative field F(x,y,z) = 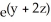 (i + x j + 2x k).
(i + x j + 2x k).
A) x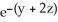 = C
= C
B) x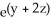 = C
= C
C)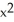
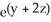 = C
= C
D) x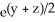 = C
= C
E) y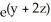 = C
= C
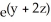 (i + x j + 2x k).
(i + x j + 2x k).A) x
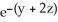 = C
= CB) x
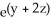 = C
= CC)
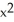
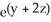 = C
= CD) x
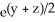 = C
= CE) y
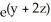 = C
= C
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
21
(a)In terms of polar coordinates r and , describe the field lines of the conservative plane vector field F(x,y) = x i + y j.
(b) In terms of polar coordinates r and , describe the equipotential curves of the conservative plane vector field F(x,y) = x i + y j.
A) (a) radial lines =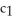 (b) circles r =
(b) circles r = 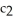
B) (a) circles r =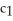 (b) radial lines =
(b) radial lines = 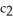
C) (a) circles r =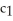 sin( ) (b) circles r =
sin( ) (b) circles r = 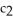 cos( )
cos( )
D) (a) lines r cos =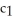 (b) lines r sin =
(b) lines r sin = 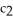
E) (a) lines r cos =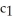 (b) radial lines =
(b) radial lines = 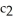
(b) In terms of polar coordinates r and , describe the equipotential curves of the conservative plane vector field F(x,y) = x i + y j.
A) (a) radial lines =
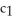 (b) circles r =
(b) circles r = 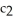
B) (a) circles r =
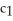 (b) radial lines =
(b) radial lines = 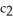
C) (a) circles r =
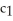 sin( ) (b) circles r =
sin( ) (b) circles r = 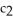 cos( )
cos( )D) (a) lines r cos =
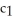 (b) lines r sin =
(b) lines r sin = 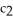
E) (a) lines r cos =
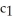 (b) radial lines =
(b) radial lines = 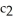

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
22
Which of the following three vector fields is conservative?
F = (4xz + 4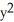 ) i + (xy +
) i + (xy + 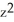 ) j + (2yz + 2
) j + (2yz + 2 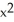 ) k,
) k,
G = 7xy j
H = F + G
A) only F
B) only G
C) only H
D) only F and G
E) All three are conservative.
F = (4xz + 4
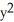 ) i + (xy +
) i + (xy + 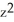 ) j + (2yz + 2
) j + (2yz + 2 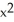 ) k,
) k,G = 7xy j
H = F + G
A) only F
B) only G
C) only H
D) only F and G
E) All three are conservative.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
23
Let F = 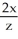 i +
i + 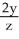 j + K
j + K 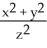 k. For what value of the constant K is F conservative?
k. For what value of the constant K is F conservative?
If K has that value, find the family of equipotential surfaces of F.
A) K = -1, z = C(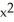 +
+ 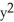 )
)
B) K = 1,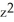 = C(
= C( 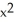 +
+ 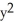 )
)
C) K = -1, z (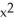 +
+ 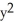 ) = C
) = C
D) K = -2,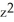 = C(
= C( 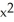 +
+ 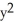 )
)
E) K = 2, z = C(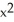 +
+ 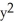 )
)
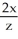 i +
i + 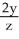 j + K
j + K 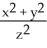 k. For what value of the constant K is F conservative?
k. For what value of the constant K is F conservative?If K has that value, find the family of equipotential surfaces of F.
A) K = -1, z = C(
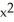 +
+ 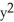 )
)B) K = 1,
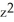 = C(
= C( 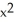 +
+ 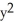 )
)C) K = -1, z (
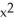 +
+ 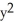 ) = C
) = CD) K = -2,
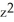 = C(
= C( 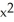 +
+ 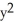 )
)E) K = 2, z = C(
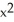 +
+ 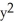 )
)
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
24
If F and G are plane conservative vector fields with potentials 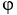 and
and 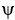 , respectively, then the vector field H = 3F - 2G is also conservative with potential 311ee7ba1_f0bb_6cc5_ae82_7109d7d2775a_TB9661_11 - 2https://storage.examlex.com/TB9661/11ee7ba1_ff03_9556_ae82_45b7421486b4_TB9661_11.
, respectively, then the vector field H = 3F - 2G is also conservative with potential 311ee7ba1_f0bb_6cc5_ae82_7109d7d2775a_TB9661_11 - 2https://storage.examlex.com/TB9661/11ee7ba1_ff03_9556_ae82_45b7421486b4_TB9661_11.
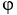 and
and 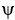 , respectively, then the vector field H = 3F - 2G is also conservative with potential 311ee7ba1_f0bb_6cc5_ae82_7109d7d2775a_TB9661_11 - 2https://storage.examlex.com/TB9661/11ee7ba1_ff03_9556_ae82_45b7421486b4_TB9661_11.
, respectively, then the vector field H = 3F - 2G is also conservative with potential 311ee7ba1_f0bb_6cc5_ae82_7109d7d2775a_TB9661_11 - 2https://storage.examlex.com/TB9661/11ee7ba1_ff03_9556_ae82_45b7421486b4_TB9661_11.
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
25
The gradient of a scalar field ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the constant real numbers a and b such that the vector field F = cos(2 \theta ) + a sin(2 \theta ) is conservative.</strong> A) a = 1 , b = -1 B) a = -1 , b = 2 C) a = - , b = 2 D) a = - , b = 2 E) a = , b = -2](https://storage.examlex.com/TB9661/11ee7ba1_f0bb_6cc5_ae82_7109d7d2775a_TB9661_11.jpg) expressed in terms of polar coordinates [r, ] in the plane is
expressed in terms of polar coordinates [r, ] in the plane is![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the constant real numbers a and b such that the vector field F = cos(2 \theta ) + a sin(2 \theta ) is conservative.</strong> A) a = 1 , b = -1 B) a = -1 , b = 2 C) a = - , b = 2 D) a = - , b = 2 E) a = , b = -2](https://storage.examlex.com/TB9661/11ee7ba2_4068_4e57_ae82_01d6039f494d_TB9661_11.jpg) (r, ) =
(r, ) = ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the constant real numbers a and b such that the vector field F = cos(2 \theta ) + a sin(2 \theta ) is conservative.</strong> A) a = 1 , b = -1 B) a = -1 , b = 2 C) a = - , b = 2 D) a = - , b = 2 E) a = , b = -2](https://storage.examlex.com/TB9661/11ee77e1_779d_79b6_a0f8_b357e82de6cc_TB9661_11.jpg)
![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the constant real numbers a and b such that the vector field F = cos(2 \theta ) + a sin(2 \theta ) is conservative.</strong> A) a = 1 , b = -1 B) a = -1 , b = 2 C) a = - , b = 2 D) a = - , b = 2 E) a = , b = -2](https://storage.examlex.com/TB9661/11ee77e1_779d_79b7_a0f8_ef07a08e17ba_TB9661_11.jpg) +
+ ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the constant real numbers a and b such that the vector field F = cos(2 \theta ) + a sin(2 \theta ) is conservative.</strong> A) a = 1 , b = -1 B) a = -1 , b = 2 C) a = - , b = 2 D) a = - , b = 2 E) a = , b = -2](https://storage.examlex.com/TB9661/11ee77e1_779d_79b8_a0f8_5931186181c6_TB9661_11.jpg) .
. ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the constant real numbers a and b such that the vector field F = cos(2 \theta ) + a sin(2 \theta ) is conservative.</strong> A) a = 1 , b = -1 B) a = -1 , b = 2 C) a = - , b = 2 D) a = - , b = 2 E) a = , b = -2](https://storage.examlex.com/TB9661/11ee77e1_779d_79b9_a0f8_91dbeb59c2f4_TB9661_11.jpg)
![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the constant real numbers a and b such that the vector field F = cos(2 \theta ) + a sin(2 \theta ) is conservative.</strong> A) a = 1 , b = -1 B) a = -1 , b = 2 C) a = - , b = 2 D) a = - , b = 2 E) a = , b = -2](https://storage.examlex.com/TB9661/11ee77e1_779d_79ba_a0f8_e173583e9e49_TB9661_11.jpg) Use the result above to find the constant real numbers a and b such that the vector field F =
Use the result above to find the constant real numbers a and b such that the vector field F = ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the constant real numbers a and b such that the vector field F = cos(2 \theta ) + a sin(2 \theta ) is conservative.</strong> A) a = 1 , b = -1 B) a = -1 , b = 2 C) a = - , b = 2 D) a = - , b = 2 E) a = , b = -2](https://storage.examlex.com/TB9661/11ee77e1_779d_79bb_a0f8_9d0671ae54b1_TB9661_11.jpg) cos(2 )
cos(2 ) ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the constant real numbers a and b such that the vector field F = cos(2 \theta ) + a sin(2 \theta ) is conservative.</strong> A) a = 1 , b = -1 B) a = -1 , b = 2 C) a = - , b = 2 D) a = - , b = 2 E) a = , b = -2](https://storage.examlex.com/TB9661/11ee77e1_779d_79bc_a0f8_7558dac33989_TB9661_11.jpg) + a
+ a ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the constant real numbers a and b such that the vector field F = cos(2 \theta ) + a sin(2 \theta ) is conservative.</strong> A) a = 1 , b = -1 B) a = -1 , b = 2 C) a = - , b = 2 D) a = - , b = 2 E) a = , b = -2](https://storage.examlex.com/TB9661/11ee77e1_779d_79bd_a0f8_2b49b90ec27c_TB9661_11.jpg) sin(2 )
sin(2 ) ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the constant real numbers a and b such that the vector field F = cos(2 \theta ) + a sin(2 \theta ) is conservative.</strong> A) a = 1 , b = -1 B) a = -1 , b = 2 C) a = - , b = 2 D) a = - , b = 2 E) a = , b = -2](https://storage.examlex.com/TB9661/11ee77e1_779d_79be_a0f8_c54b6757e295_TB9661_11.jpg) is conservative.
is conservative.
A) a = 1 , b = -1
B) a = -1 , b = 2
C) a = -![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the constant real numbers a and b such that the vector field F = cos(2 \theta ) + a sin(2 \theta ) is conservative.</strong> A) a = 1 , b = -1 B) a = -1 , b = 2 C) a = - , b = 2 D) a = - , b = 2 E) a = , b = -2](https://storage.examlex.com/TB9661/11ee77e1_779d_79bf_a0f8_891e91b2e9e3_TB9661_11.jpg) , b = 2
, b = 2
D) a = -![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the constant real numbers a and b such that the vector field F = cos(2 \theta ) + a sin(2 \theta ) is conservative.</strong> A) a = 1 , b = -1 B) a = -1 , b = 2 C) a = - , b = 2 D) a = - , b = 2 E) a = , b = -2](https://storage.examlex.com/TB9661/11ee77e1_779d_79c0_a0f8_d7d933ac81f9_TB9661_11.jpg) , b = 2
, b = 2
E) a =![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the constant real numbers a and b such that the vector field F = cos(2 \theta ) + a sin(2 \theta ) is conservative.</strong> A) a = 1 , b = -1 B) a = -1 , b = 2 C) a = - , b = 2 D) a = - , b = 2 E) a = , b = -2](https://storage.examlex.com/TB9661/11ee77e1_779d_79c1_a0f8_d93d9e48aff9_TB9661_11.jpg) , b = -2
, b = -2
![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the constant real numbers a and b such that the vector field F = cos(2 \theta ) + a sin(2 \theta ) is conservative.</strong> A) a = 1 , b = -1 B) a = -1 , b = 2 C) a = - , b = 2 D) a = - , b = 2 E) a = , b = -2](https://storage.examlex.com/TB9661/11ee7ba1_f0bb_6cc5_ae82_7109d7d2775a_TB9661_11.jpg) expressed in terms of polar coordinates [r, ] in the plane is
expressed in terms of polar coordinates [r, ] in the plane is![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the constant real numbers a and b such that the vector field F = cos(2 \theta ) + a sin(2 \theta ) is conservative.</strong> A) a = 1 , b = -1 B) a = -1 , b = 2 C) a = - , b = 2 D) a = - , b = 2 E) a = , b = -2](https://storage.examlex.com/TB9661/11ee7ba2_4068_4e57_ae82_01d6039f494d_TB9661_11.jpg) (r, ) =
(r, ) = ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the constant real numbers a and b such that the vector field F = cos(2 \theta ) + a sin(2 \theta ) is conservative.</strong> A) a = 1 , b = -1 B) a = -1 , b = 2 C) a = - , b = 2 D) a = - , b = 2 E) a = , b = -2](https://storage.examlex.com/TB9661/11ee77e1_779d_79b6_a0f8_b357e82de6cc_TB9661_11.jpg)
![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the constant real numbers a and b such that the vector field F = cos(2 \theta ) + a sin(2 \theta ) is conservative.</strong> A) a = 1 , b = -1 B) a = -1 , b = 2 C) a = - , b = 2 D) a = - , b = 2 E) a = , b = -2](https://storage.examlex.com/TB9661/11ee77e1_779d_79b7_a0f8_ef07a08e17ba_TB9661_11.jpg) +
+ ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the constant real numbers a and b such that the vector field F = cos(2 \theta ) + a sin(2 \theta ) is conservative.</strong> A) a = 1 , b = -1 B) a = -1 , b = 2 C) a = - , b = 2 D) a = - , b = 2 E) a = , b = -2](https://storage.examlex.com/TB9661/11ee77e1_779d_79b8_a0f8_5931186181c6_TB9661_11.jpg) .
. ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the constant real numbers a and b such that the vector field F = cos(2 \theta ) + a sin(2 \theta ) is conservative.</strong> A) a = 1 , b = -1 B) a = -1 , b = 2 C) a = - , b = 2 D) a = - , b = 2 E) a = , b = -2](https://storage.examlex.com/TB9661/11ee77e1_779d_79b9_a0f8_91dbeb59c2f4_TB9661_11.jpg)
![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the constant real numbers a and b such that the vector field F = cos(2 \theta ) + a sin(2 \theta ) is conservative.</strong> A) a = 1 , b = -1 B) a = -1 , b = 2 C) a = - , b = 2 D) a = - , b = 2 E) a = , b = -2](https://storage.examlex.com/TB9661/11ee77e1_779d_79ba_a0f8_e173583e9e49_TB9661_11.jpg) Use the result above to find the constant real numbers a and b such that the vector field F =
Use the result above to find the constant real numbers a and b such that the vector field F = ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the constant real numbers a and b such that the vector field F = cos(2 \theta ) + a sin(2 \theta ) is conservative.</strong> A) a = 1 , b = -1 B) a = -1 , b = 2 C) a = - , b = 2 D) a = - , b = 2 E) a = , b = -2](https://storage.examlex.com/TB9661/11ee77e1_779d_79bb_a0f8_9d0671ae54b1_TB9661_11.jpg) cos(2 )
cos(2 ) ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the constant real numbers a and b such that the vector field F = cos(2 \theta ) + a sin(2 \theta ) is conservative.</strong> A) a = 1 , b = -1 B) a = -1 , b = 2 C) a = - , b = 2 D) a = - , b = 2 E) a = , b = -2](https://storage.examlex.com/TB9661/11ee77e1_779d_79bc_a0f8_7558dac33989_TB9661_11.jpg) + a
+ a ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the constant real numbers a and b such that the vector field F = cos(2 \theta ) + a sin(2 \theta ) is conservative.</strong> A) a = 1 , b = -1 B) a = -1 , b = 2 C) a = - , b = 2 D) a = - , b = 2 E) a = , b = -2](https://storage.examlex.com/TB9661/11ee77e1_779d_79bd_a0f8_2b49b90ec27c_TB9661_11.jpg) sin(2 )
sin(2 ) ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the constant real numbers a and b such that the vector field F = cos(2 \theta ) + a sin(2 \theta ) is conservative.</strong> A) a = 1 , b = -1 B) a = -1 , b = 2 C) a = - , b = 2 D) a = - , b = 2 E) a = , b = -2](https://storage.examlex.com/TB9661/11ee77e1_779d_79be_a0f8_c54b6757e295_TB9661_11.jpg) is conservative.
is conservative.A) a = 1 , b = -1
B) a = -1 , b = 2
C) a = -
![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the constant real numbers a and b such that the vector field F = cos(2 \theta ) + a sin(2 \theta ) is conservative.</strong> A) a = 1 , b = -1 B) a = -1 , b = 2 C) a = - , b = 2 D) a = - , b = 2 E) a = , b = -2](https://storage.examlex.com/TB9661/11ee77e1_779d_79bf_a0f8_891e91b2e9e3_TB9661_11.jpg) , b = 2
, b = 2D) a = -
![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the constant real numbers a and b such that the vector field F = cos(2 \theta ) + a sin(2 \theta ) is conservative.</strong> A) a = 1 , b = -1 B) a = -1 , b = 2 C) a = - , b = 2 D) a = - , b = 2 E) a = , b = -2](https://storage.examlex.com/TB9661/11ee77e1_779d_79c0_a0f8_d7d933ac81f9_TB9661_11.jpg) , b = 2
, b = 2E) a =
![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the result above to find the constant real numbers a and b such that the vector field F = cos(2 \theta ) + a sin(2 \theta ) is conservative.</strong> A) a = 1 , b = -1 B) a = -1 , b = 2 C) a = - , b = 2 D) a = - , b = 2 E) a = , b = -2](https://storage.examlex.com/TB9661/11ee77e1_779d_79c1_a0f8_d93d9e48aff9_TB9661_11.jpg) , b = -2
, b = -2
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
26
The gradient of a scalar field ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee7ba1_f0bb_6cc5_ae82_7109d7d2775a_TB9661_11.jpg) expressed in terms of polar coordinates [r, ] in the plane is
expressed in terms of polar coordinates [r, ] in the plane is![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee7ba2_4068_4e57_ae82_01d6039f494d_TB9661_11.jpg) (r, ) =
(r, ) = ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_a0d2_a0f8_91c9c22e1802_TB9661_11.jpg)
![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_a0d3_a0f8_853fffb7d8d6_TB9661_11.jpg) +
+ ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_a0d4_a0f8_9d7ab561f873_TB9661_11.jpg) .
. ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_a0d5_a0f8_09b1b9fe8682_TB9661_11.jpg)
![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_a0d6_a0f8_31655b487c77_TB9661_11.jpg) Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3
Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_a0d7_a0f8_477e6d734247_TB9661_11.jpg) cos( )
cos( ) ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_a0d8_a0f8_473150b92b47_TB9661_11.jpg) -
- ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_a0d9_a0f8_c973a6067ff2_TB9661_11.jpg) sin( )
sin( ) ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_a0da_a0f8_f9a3d36cb5eb_TB9661_11.jpg) .
.
A) 4![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_a0db_a0f8_65e4b0ee013f_TB9661_11.jpg) cos( ) + C
cos( ) + C
B) - 8r sin( ) + C
C)![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_a0dc_a0f8_2fc89a5fcb5c_TB9661_11.jpg) cos( )
cos( ) ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_a0dd_a0f8_b1c968b6dd56_TB9661_11.jpg) +
+ ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_a0de_a0f8_e75b4a946698_TB9661_11.jpg) cos( )
cos( ) ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_a0df_a0f8_3ddef973780d_TB9661_11.jpg)
D)![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_a0e0_a0f8_8ffacc0474ee_TB9661_11.jpg) cos( ) + C
cos( ) + C
E)![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_c7f1_a0f8_455e7477d61b_TB9661_11.jpg) cos( )
cos( ) ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_c7f2_a0f8_47b2303e4789_TB9661_11.jpg) +
+ ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_c7f3_a0f8_8d212b06890c_TB9661_11.jpg) cos( )
cos( ) ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_c7f4_a0f8_2d2acba4d298_TB9661_11.jpg) + C
+ C
![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee7ba1_f0bb_6cc5_ae82_7109d7d2775a_TB9661_11.jpg) expressed in terms of polar coordinates [r, ] in the plane is
expressed in terms of polar coordinates [r, ] in the plane is![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee7ba2_4068_4e57_ae82_01d6039f494d_TB9661_11.jpg) (r, ) =
(r, ) = ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_a0d2_a0f8_91c9c22e1802_TB9661_11.jpg)
![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_a0d3_a0f8_853fffb7d8d6_TB9661_11.jpg) +
+ ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_a0d4_a0f8_9d7ab561f873_TB9661_11.jpg) .
. ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_a0d5_a0f8_09b1b9fe8682_TB9661_11.jpg)
![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_a0d6_a0f8_31655b487c77_TB9661_11.jpg) Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3
Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_a0d7_a0f8_477e6d734247_TB9661_11.jpg) cos( )
cos( ) ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_a0d8_a0f8_473150b92b47_TB9661_11.jpg) -
- ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_a0d9_a0f8_c973a6067ff2_TB9661_11.jpg) sin( )
sin( ) ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_a0da_a0f8_f9a3d36cb5eb_TB9661_11.jpg) .
.A) 4
![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_a0db_a0f8_65e4b0ee013f_TB9661_11.jpg) cos( ) + C
cos( ) + CB) - 8r sin( ) + C
C)
![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_a0dc_a0f8_2fc89a5fcb5c_TB9661_11.jpg) cos( )
cos( ) ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_a0dd_a0f8_b1c968b6dd56_TB9661_11.jpg) +
+ ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_a0de_a0f8_e75b4a946698_TB9661_11.jpg) cos( )
cos( ) ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_a0df_a0f8_3ddef973780d_TB9661_11.jpg)
D)
![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_a0e0_a0f8_8ffacc0474ee_TB9661_11.jpg) cos( ) + C
cos( ) + CE)
![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_c7f1_a0f8_455e7477d61b_TB9661_11.jpg) cos( )
cos( ) ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_c7f2_a0f8_47b2303e4789_TB9661_11.jpg) +
+ ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_c7f3_a0f8_8d212b06890c_TB9661_11.jpg) cos( )
cos( ) ![<strong>The gradient of a scalar field expressed in terms of polar coordinates [r, \theta ] in the plane is (r, \theta ) = + . Use the above result to find a potential function for the conservative vector field (expressed in polar form) F = 3 cos( \theta ) - sin( \theta ) .</strong> A) 4 cos( \theta ) + C B) - 8r sin( \theta ) + C C) cos( \theta ) + cos( \theta ) D) cos( \theta ) + C E) cos( \theta ) + cos( \theta ) + C](https://storage.examlex.com/TB9661/11ee77e1_779d_c7f4_a0f8_2d2acba4d298_TB9661_11.jpg) + C
+ C
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
27
A potential function of a vector field F is given by 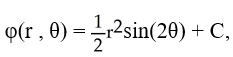 , where (r , θ) are the polar coordinates and C is an arbitrary constant. Find F.
, where (r , θ) are the polar coordinates and C is an arbitrary constant. Find F.
Hint: The gradient of g(r , θ) is given by ∇g(r , θ) =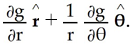 .
.
A) r sin(2 ) + r cos(2 )
B) r sin(2 ) + r cos(2 )
+ r cos(2 ) 
C) r sin(2 ) - r cos(2 )
- r cos(2 ) 
D) r sin(2 ) +
+  r cos(2 )
r cos(2 ) 
E) r sin(2 ) - r cos(2 )
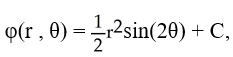 , where (r , θ) are the polar coordinates and C is an arbitrary constant. Find F.
, where (r , θ) are the polar coordinates and C is an arbitrary constant. Find F.Hint: The gradient of g(r , θ) is given by ∇g(r , θ) =
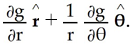 .
.A) r sin(2 ) + r cos(2 )
B) r sin(2 )
 + r cos(2 )
+ r cos(2 ) 
C) r sin(2 )
 - r cos(2 )
- r cos(2 ) 
D) r sin(2 )
 +
+  r cos(2 )
r cos(2 ) 
E) r sin(2 ) - r cos(2 )

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
28
Describe the family of equipotential curves and the family of field lines for the conservative vector field F = x i - yj . Sketch at least four members of each family.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
29
Evaluate the integral 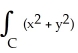 ds once around the square C in the xy-plane with vertices (± 1, 1) and (± 1, -1).
ds once around the square C in the xy-plane with vertices (± 1, 1) and (± 1, -1).
A)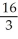
B)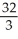
C) 8
D) 11
E)
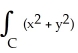 ds once around the square C in the xy-plane with vertices (± 1, 1) and (± 1, -1).
ds once around the square C in the xy-plane with vertices (± 1, 1) and (± 1, -1).A)
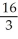
B)
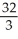
C) 8
D) 11
E)


Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
30
Use a line integral to find the mass of a wire running along the curve y = 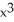 from (0, 0) to (1, 1) if the density (mass per unit length) of the wire at any point (x, y) is numerically equal to y.
from (0, 0) to (1, 1) if the density (mass per unit length) of the wire at any point (x, y) is numerically equal to y.
A)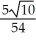 -
- 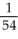
B)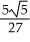 -
- 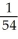
C)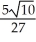 -
- 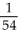
D)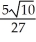 -
- 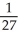
E)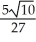 +
+ 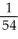
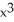 from (0, 0) to (1, 1) if the density (mass per unit length) of the wire at any point (x, y) is numerically equal to y.
from (0, 0) to (1, 1) if the density (mass per unit length) of the wire at any point (x, y) is numerically equal to y.A)
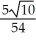 -
- 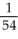
B)
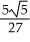 -
- 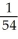
C)
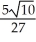 -
- 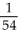
D)
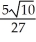 -
- 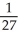
E)
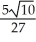 +
+ 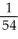

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
31
Evaluate the line integral 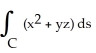 along the straight line from (1, 2, -1) to (3, 2, 5).
along the straight line from (1, 2, -1) to (3, 2, 5).
A)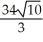
B)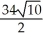
C)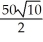
D)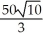
E)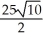
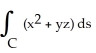 along the straight line from (1, 2, -1) to (3, 2, 5).
along the straight line from (1, 2, -1) to (3, 2, 5).A)
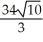
B)
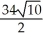
C)
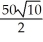
D)
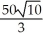
E)
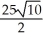

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
32
Evaluate the line integral 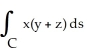 along the first octant part of y =
along the first octant part of y = 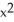 , z + y = 1 from (0, 0, 1) to (1, 1, 0).
, z + y = 1 from (0, 0, 1) to (1, 1, 0).
A)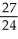
B)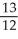
C)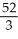
D) 18
E)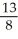
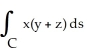 along the first octant part of y =
along the first octant part of y = 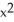 , z + y = 1 from (0, 0, 1) to (1, 1, 0).
, z + y = 1 from (0, 0, 1) to (1, 1, 0).A)
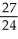
B)
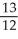
C)
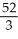
D) 18
E)
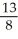

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
33
Evaluate the line integral 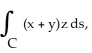 where C is the curve y = x, z = 1 +
where C is the curve y = x, z = 1 + 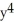 , from (-1, -1, 2) to (1, 1, 2).
, from (-1, -1, 2) to (1, 1, 2).
A) 2
B) 1
C) 0
D) -1
E) -2
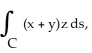 where C is the curve y = x, z = 1 +
where C is the curve y = x, z = 1 + 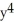 , from (-1, -1, 2) to (1, 1, 2).
, from (-1, -1, 2) to (1, 1, 2).A) 2
B) 1
C) 0
D) -1
E) -2

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
34
Evaluate the line integral 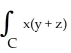 ds, where C is that part of the line of intersection of the two planes 4x - y - z = -1 and 2x - 3y + 2z = 2 from (0, 0, 1) to (1, 2, 3).
ds, where C is that part of the line of intersection of the two planes 4x - y - z = -1 and 2x - 3y + 2z = 2 from (0, 0, 1) to (1, 2, 3).
A)
B)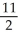
C) 6
D)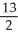
E) 5
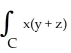 ds, where C is that part of the line of intersection of the two planes 4x - y - z = -1 and 2x - 3y + 2z = 2 from (0, 0, 1) to (1, 2, 3).
ds, where C is that part of the line of intersection of the two planes 4x - y - z = -1 and 2x - 3y + 2z = 2 from (0, 0, 1) to (1, 2, 3).A)

B)
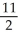
C) 6
D)
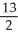
E) 5

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
35
Find the integral 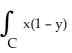 ds, where C is the first octant portion of the curve of intersection of the cylinder x2 + (y - 1)2 = 1 and the plane x + z = 1.
ds, where C is the first octant portion of the curve of intersection of the cylinder x2 + (y - 1)2 = 1 and the plane x + z = 1.
A) (1 - 2
(1 - 2 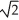 )
)
B) (1 - 2
(1 - 2 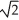 )
)
C) (2
(2 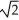 - 1)
- 1)
D) (2
(2 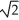 - 1)
- 1)
E) 0
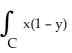 ds, where C is the first octant portion of the curve of intersection of the cylinder x2 + (y - 1)2 = 1 and the plane x + z = 1.
ds, where C is the first octant portion of the curve of intersection of the cylinder x2 + (y - 1)2 = 1 and the plane x + z = 1.A)
 (1 - 2
(1 - 2 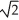 )
)B)
 (1 - 2
(1 - 2 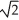 )
)C)
 (2
(2 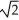 - 1)
- 1)D)
 (2
(2 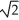 - 1)
- 1)E) 0

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
36
Let C be the curve of intersection of the paraboloid z = 6 - x2 - y2 and the cone z = 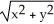 .Find the mass of the wire having the shape of the curve C if the line density function is given by
.Find the mass of the wire having the shape of the curve C if the line density function is given by 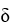 (x, y, z) = z
(x, y, z) = z 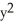 .
.
A)
B) 81
C) 16
D)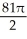
E) 8
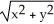 .Find the mass of the wire having the shape of the curve C if the line density function is given by
.Find the mass of the wire having the shape of the curve C if the line density function is given by  (x, y, z) = z
(x, y, z) = z 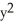 .
.A)
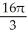
B) 81
C) 16
D)
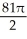
E) 8

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
37
Find 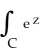 ds along the curve r =
ds along the curve r = 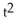 i +
i + 
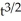 j + t k, 0 t l.
j + t k, 0 t l.
A) 5e -3
B) e + 1
C) 2e - 1
D) e - 1
E) 2e
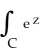 ds along the curve r =
ds along the curve r = 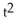 i +
i + 
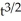 j + t k, 0 t l.
j + t k, 0 t l.A) 5e -3
B) e + 1
C) 2e - 1
D) e - 1
E) 2e

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
38
Find 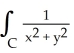 ds along the entire line 3x + 4y = 10. (Hint: Use symmetry to replace the line with a horizontal line at the same distance from the origin.)
ds along the entire line 3x + 4y = 10. (Hint: Use symmetry to replace the line with a horizontal line at the same distance from the origin.)
A)
B)
C) 2
D)
E)
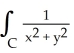 ds along the entire line 3x + 4y = 10. (Hint: Use symmetry to replace the line with a horizontal line at the same distance from the origin.)
ds along the entire line 3x + 4y = 10. (Hint: Use symmetry to replace the line with a horizontal line at the same distance from the origin.)A)
B)
C) 2
D)

E)


Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
39
Use the definition of the line integral to evaluate 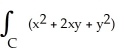 dx, where C is the graph of x + y = 5 with initial point (1, 4) and terminal point (0, 5).
dx, where C is the graph of x + y = 5 with initial point (1, 4) and terminal point (0, 5).
A) -24
B) -25
C) -26
D) -27
E) -23
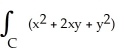 dx, where C is the graph of x + y = 5 with initial point (1, 4) and terminal point (0, 5).
dx, where C is the graph of x + y = 5 with initial point (1, 4) and terminal point (0, 5).A) -24
B) -25
C) -26
D) -27
E) -23

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
40
Find the work done by the force field F(x, y, z) = x i + 3xy j - (x + z) k on a particle moving along the line segment from (1, 4, 2) to (0, 5, 1).
A) 2
B) 10
C) 12
D) 8
E) 16
A) 2
B) 10
C) 12
D) 8
E) 16

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
41
Find 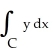 + z dy + x dz where C is part of the helix r(t) = sin t i + cos t j + t k, 0 t .
+ z dy + x dz where C is part of the helix r(t) = sin t i + cos t j + t k, 0 t .
A) 2 +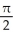
B) 2 -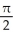
C) 2 -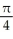
D) 2 +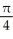
E) 1 -
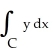 + z dy + x dz where C is part of the helix r(t) = sin t i + cos t j + t k, 0 t .
+ z dy + x dz where C is part of the helix r(t) = sin t i + cos t j + t k, 0 t .A) 2 +
B) 2 -
C) 2 -
D) 2 +
E) 1 -

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
42
If F = -y i + x j + z k, calculate 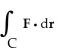 where C is the straight line segment from(1, 0, 0) to (-1, 0, ).
where C is the straight line segment from(1, 0, 0) to (-1, 0, ).
A)
B)
C) 1
D)
E)
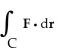 where C is the straight line segment from(1, 0, 0) to (-1, 0, ).
where C is the straight line segment from(1, 0, 0) to (-1, 0, ).A)
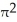
B)
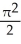
C) 1
D)

E)

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
43
Let  =
= 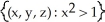 ,
, 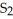 =
=  and
and 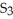 =
= 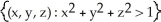 be sets of points in 3-space. Determine whether the set is a connected or a simply connected set.
be sets of points in 3-space. Determine whether the set is a connected or a simply connected set.
A) S1 is simply connected.
B) S2 is not connected.
C) S1 is connected but not simply connected.
D) S3 is simply connected.
E) S3 is connected but not simply connected.
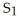 =
= 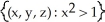 ,
,  =
=  and
and 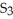 =
= 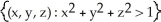 be sets of points in 3-space. Determine whether the set is a connected or a simply connected set.
be sets of points in 3-space. Determine whether the set is a connected or a simply connected set.A) S1 is simply connected.
B) S2 is not connected.
C) S1 is connected but not simply connected.
D) S3 is simply connected.
E) S3 is connected but not simply connected.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
44
Let F be a smooth conservative force field defined in 2-space with a potential function 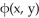 , and let C be the curve shown in the figure below. Find the work done by the force field F in moving a particle along the curve C from P to R given that φ(1,- 2) = -17, andφ(4, 1) = 3.
, and let C be the curve shown in the figure below. Find the work done by the force field F in moving a particle along the curve C from P to R given that φ(1,- 2) = -17, andφ(4, 1) = 3. 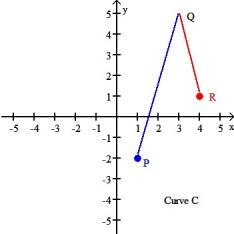
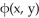 , and let C be the curve shown in the figure below. Find the work done by the force field F in moving a particle along the curve C from P to R given that φ(1,- 2) = -17, andφ(4, 1) = 3.
, and let C be the curve shown in the figure below. Find the work done by the force field F in moving a particle along the curve C from P to R given that φ(1,- 2) = -17, andφ(4, 1) = 3. 

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
45
How much work is required for the force field F = y i + 2x j to move an object along the upper part of the ellipse 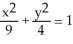 from (3, 0) to (-3, 0)?
from (3, 0) to (-3, 0)?
A) 2
B) 9
C) -9
D) -2
E) 0
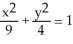 from (3, 0) to (-3, 0)?
from (3, 0) to (-3, 0)?A) 2
B) 9
C) -9
D) -2
E) 0

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
46
Let F be a vector field such that F = ∇φ - y i for some smooth scalar function φ. Evaluate 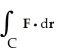 counterclockwise around the ellipse
counterclockwise around the ellipse 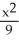 +
+ 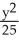 = 1.
= 1.
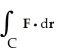 counterclockwise around the ellipse
counterclockwise around the ellipse  +
+ 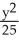 = 1.
= 1.
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
47
Evaluate the line integral 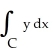 + x dy + z dz along the curve C from (1, 0, 1) to(-1, 2, 5) with parametrization
+ x dy + z dz along the curve C from (1, 0, 1) to(-1, 2, 5) with parametrization 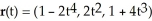 with
with 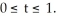
A) 9
B) 10
C) 11
D) 12
E) 8
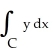 + x dy + z dz along the curve C from (1, 0, 1) to(-1, 2, 5) with parametrization
+ x dy + z dz along the curve C from (1, 0, 1) to(-1, 2, 5) with parametrization 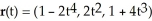 with
with 
A) 9
B) 10
C) 11
D) 12
E) 8

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
48
Evaluate the line integral 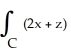 dx + 2y dy + (x + 2z) dz along the curve C with parametrization
dx + 2y dy + (x + 2z) dz along the curve C with parametrization 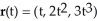 with
with 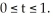
A) 14
B) 15
C) 16
D) 17
E) 18
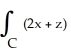 dx + 2y dy + (x + 2z) dz along the curve C with parametrization
dx + 2y dy + (x + 2z) dz along the curve C with parametrization 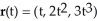 with
with 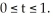
A) 14
B) 15
C) 16
D) 17
E) 18

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
49
Find the work done by the conservative force F = (2y + z) i + (2x + z) j + (x + y) k in moving a particle along the elliptical helix 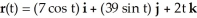 from
from 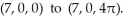
A) 28
B) 39
C) 4
D) 7
E) 16
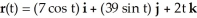 from
from 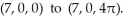
A) 28
B) 39
C) 4
D) 7
E) 16

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
50
Evaluate the line integral 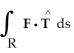 for F =
for F =  y, 0, zy
y, 0, zy  , where R is the helix
, where R is the helix 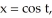
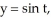
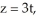
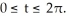
A) -20
B) -17
C) -18
D) -19
E) -21
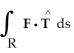 for F =
for F =  y, 0, zy
y, 0, zy  , where R is the helix
, where R is the helix 
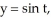
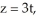
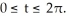
A) -20
B) -17
C) -18
D) -19
E) -21

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
51
Evaluate the line integral 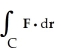 for F = (2y + z) i + (2x + z) j + (x + y) k, where C is the curve
for F = (2y + z) i + (2x + z) j + (x + y) k, where C is the curve 
A)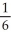
B)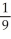
C)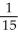
D) 0
E)
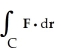 for F = (2y + z) i + (2x + z) j + (x + y) k, where C is the curve
for F = (2y + z) i + (2x + z) j + (x + y) k, where C is the curve 
A)
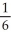
B)
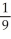
C)
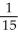
D) 0
E)


Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
52
For what value of the constant A does the line integral I = 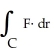 , where
, where 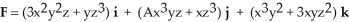 have the same value for all paths from the origin to the point
have the same value for all paths from the origin to the point 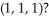 For that value of A, what is the value of the integral?
For that value of A, what is the value of the integral?
A) A = 3, I = 6
B) A = 2, I = -2
C) A = 2, I = 1
D) A = 3, I = 1
E) A = 2, I = 2
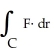 , where
, where 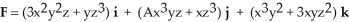 have the same value for all paths from the origin to the point
have the same value for all paths from the origin to the point 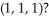 For that value of A, what is the value of the integral?
For that value of A, what is the value of the integral?A) A = 3, I = 6
B) A = 2, I = -2
C) A = 2, I = 1
D) A = 3, I = 1
E) A = 2, I = 2

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
53
Use the fact that the field F = 2x 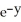 sin(z) i -
sin(z) i - 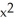
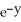 sin(z) j + (
sin(z) j + ( 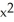
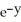 cos(z) + y) k is almost conservative (except for the last term) to help you evaluate
cos(z) + y) k is almost conservative (except for the last term) to help you evaluate 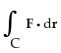 around the circle
around the circle 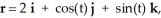
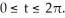
A) 2
B)
C)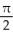
D)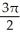
E) 0
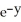 sin(z) i -
sin(z) i - 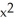
 sin(z) j + (
sin(z) j + ( 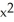
 cos(z) + y) k is almost conservative (except for the last term) to help you evaluate
cos(z) + y) k is almost conservative (except for the last term) to help you evaluate 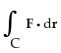 around the circle
around the circle 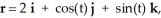
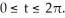
A) 2
B)
C)
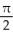
D)
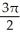
E) 0

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
54
Use the fact that the field 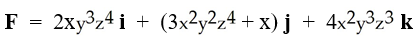 is almost conservative to help you evaluate
is almost conservative to help you evaluate 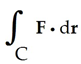 along the curve
along the curve 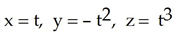 from
from 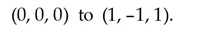
A) -
B) -
C)
D) -
E)
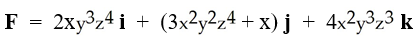 is almost conservative to help you evaluate
is almost conservative to help you evaluate 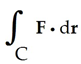 along the curve
along the curve 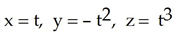 from
from 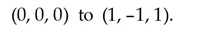
A) -

B) -

C)

D) -

E)


Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
55
Around what non-self-intersecting closed curves in the xy-plane will the line integral 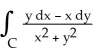 have a zero value?
have a zero value?
A) circles that pass through the origin
B) circles that are centred at the origin
C) curves bounding domains that contain the origin in their interiors
D) curves bounding domains that do not contain the origin in their interiors
E) any non-self-intersecting closed curve in the xy-plane
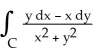 have a zero value?
have a zero value?A) circles that pass through the origin
B) circles that are centred at the origin
C) curves bounding domains that contain the origin in their interiors
D) curves bounding domains that do not contain the origin in their interiors
E) any non-self-intersecting closed curve in the xy-plane

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
56
What conditions must a domain D in the xy-plane satisfy to ensure that the value of the line integral 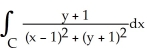 +
+ 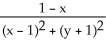 dy should depend only on the initial and terminal points of the path C that lies in D?
dy should depend only on the initial and terminal points of the path C that lies in D?
A) D must be simply connected and not contain the point (1, -1).
B) D must be connected and not contain the point (1, -1).
C) D must not contain the point (1, -1).
D) D must be simply connected and must contain the point (1, -1).
E) D can be any domain in the xy-plane.
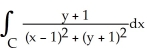 +
+ 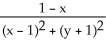 dy should depend only on the initial and terminal points of the path C that lies in D?
dy should depend only on the initial and terminal points of the path C that lies in D?A) D must be simply connected and not contain the point (1, -1).
B) D must be connected and not contain the point (1, -1).
C) D must not contain the point (1, -1).
D) D must be simply connected and must contain the point (1, -1).
E) D can be any domain in the xy-plane.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
57
Evaluate the surface integral 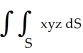 , where S is the graph of z =
, where S is the graph of z = 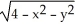 for
for 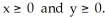
A) 2
B) 3
C) 4
D) 5
E) 1
 , where S is the graph of z =
, where S is the graph of z = 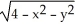 for
for 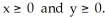
A) 2
B) 3
C) 4
D) 5
E) 1

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
58
Find the area of the surface cut from the paraboloid 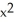 +
+ 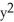 - z = 0 by the plane z = 2.
- z = 0 by the plane z = 2.
A)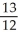 square units
square units
B)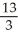 square units
square units
C)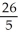 square units
square units
D)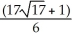 square units
square units
E)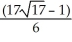 square units
square units
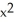 +
+ 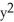 - z = 0 by the plane z = 2.
- z = 0 by the plane z = 2.A)
 square units
square unitsB)
 square units
square unitsC)
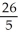 square units
square unitsD)
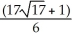 square units
square unitsE)
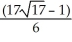 square units
square units
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
59
Evaluate the surface integral 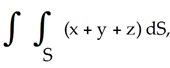 where S is the portion of the plane z = 2x - 4y above the region bounded by y = 0 , x = 1 and x = 3y in the xy-plane.
where S is the portion of the plane z = 2x - 4y above the region bounded by y = 0 , x = 1 and x = 3y in the xy-plane.
A)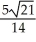
B)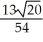
C)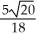
D)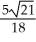
E)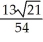
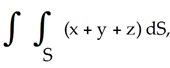 where S is the portion of the plane z = 2x - 4y above the region bounded by y = 0 , x = 1 and x = 3y in the xy-plane.
where S is the portion of the plane z = 2x - 4y above the region bounded by y = 0 , x = 1 and x = 3y in the xy-plane. A)
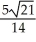
B)
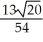
C)
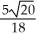
D)
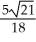
E)
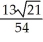

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
60
Find the area of the region cut from the plane x + 2y + 2z = 5 by the cylinder whose walls are 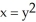 and
and 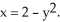
A) 2 square units
B) 3 square units
C) 4 square units
D) 6 square units
E) 1 square unit
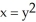 and
and 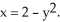
A) 2 square units
B) 3 square units
C) 4 square units
D) 6 square units
E) 1 square unit

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
61
Evaluate the surface integral 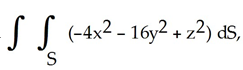 where S is the portion of the plane z = 2x - 4y above the region bounded by y = 0 , x = 1 and x = 3y in the xy-plane.
where S is the portion of the plane z = 2x - 4y above the region bounded by y = 0 , x = 1 and x = 3y in the xy-plane.
A) -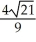
B) -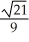
C)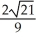
D) -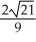
E)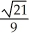
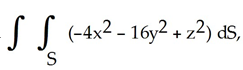 where S is the portion of the plane z = 2x - 4y above the region bounded by y = 0 , x = 1 and x = 3y in the xy-plane.
where S is the portion of the plane z = 2x - 4y above the region bounded by y = 0 , x = 1 and x = 3y in the xy-plane. A) -
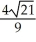
B) -
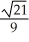
C)
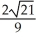
D) -
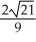
E)
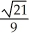

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
62
Find the area of the ellipse cut from the plane z = cx by the cylinder 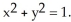 (c is constant.)
(c is constant.)
A)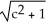 square units
square units
B)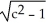 square units
square units
C) 2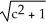 square units
square units
D)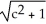 square units
square units
E)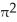
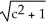 square units
square units
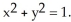 (c is constant.)
(c is constant.)A)
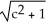 square units
square unitsB)
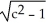 square units
square unitsC) 2
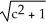 square units
square unitsD)
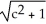 square units
square unitsE)
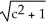 square units
square units
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
63
Evaluate the surface integral 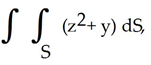 where S is the portion of the plane x + y + z = 1 inside the cylinder x2 + y2 = 1
where S is the portion of the plane x + y + z = 1 inside the cylinder x2 + y2 = 1
A)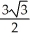
B)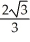
C)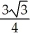
D)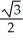
E)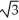
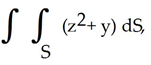 where S is the portion of the plane x + y + z = 1 inside the cylinder x2 + y2 = 1
where S is the portion of the plane x + y + z = 1 inside the cylinder x2 + y2 = 1 A)
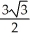
B)
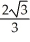
C)
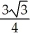
D)
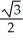
E)
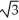

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
64
Evaluate the surface integral 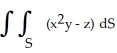 , where S is the portion of the plane
, where S is the portion of the plane 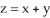 above the region R bounded by
above the region R bounded by 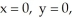 and
and 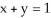 in the xy-plane.
in the xy-plane.
A)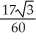
B) -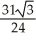
C)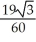
D) -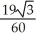
E) -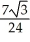
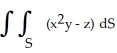 , where S is the portion of the plane
, where S is the portion of the plane 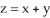 above the region R bounded by
above the region R bounded by 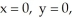 and
and 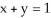 in the xy-plane.
in the xy-plane.A)
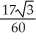
B) -
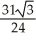
C)
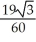
D) -
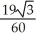
E) -
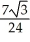

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
65
Find 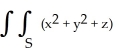 dS, where S is the part of the paraboloid
dS, where S is the part of the paraboloid 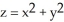 that lies above the ring
that lies above the ring 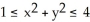 in the xy-plane.
in the xy-plane.
A)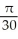 (25
(25 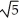 + 1)
+ 1)
B)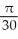 (391
(391 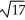 + 1)
+ 1)
C)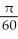 (391
(391 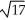 - 25
- 25 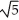 )
)
D)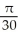 (391
(391 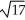 - 25
- 25 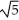 )
)
E)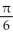 (1235
(1235 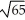 - 5
- 5 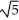 )
)
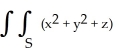 dS, where S is the part of the paraboloid
dS, where S is the part of the paraboloid 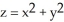 that lies above the ring
that lies above the ring 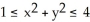 in the xy-plane.
in the xy-plane.A)
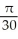 (25
(25 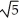 + 1)
+ 1)B)
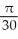 (391
(391 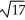 + 1)
+ 1)C)
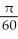 (391
(391 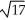 - 25
- 25 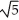 )
)D)
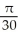 (391
(391 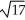 - 25
- 25 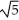 )
)E)
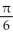 (1235
(1235 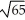 - 5
- 5 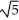 )
)
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
66
Evaluate the surface integral 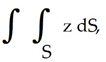 where S is the entire surface x + y + z = 1 lying in the first octant.
where S is the entire surface x + y + z = 1 lying in the first octant.
A)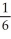
B)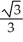
C)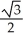
D)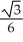
E)
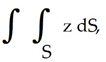 where S is the entire surface x + y + z = 1 lying in the first octant.
where S is the entire surface x + y + z = 1 lying in the first octant.A)
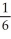
B)
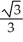
C)
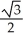
D)
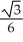
E)


Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
67
Find the area of the part of the surface 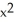 - 2 ln x +
- 2 ln x + 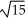 y - z = 0 inside the prism bounded by the planes x = 1, x = 2, y = 0, and y = 1.
y - z = 0 inside the prism bounded by the planes x = 1, x = 2, y = 0, and y = 1.
A) 2 + 2 ln 2 square units
B) 3 + 2 ln 2 square units
C) 4 + ln 2 square units
D) 5 + 2 ln 2 square units
E) + ln 2 square units
+ ln 2 square units
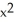 - 2 ln x +
- 2 ln x + 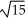 y - z = 0 inside the prism bounded by the planes x = 1, x = 2, y = 0, and y = 1.
y - z = 0 inside the prism bounded by the planes x = 1, x = 2, y = 0, and y = 1.A) 2 + 2 ln 2 square units
B) 3 + 2 ln 2 square units
C) 4 + ln 2 square units
D) 5 + 2 ln 2 square units
E)
 + ln 2 square units
+ ln 2 square units
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
68
Evaluate the surface integral 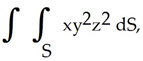 where S is the portion of the cone
where S is the portion of the cone 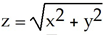 above the quarter disk
above the quarter disk 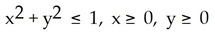 in the xy-plane.
in the xy-plane.
A)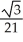
B)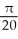
C)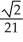
D)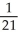
E) 0
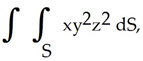 where S is the portion of the cone
where S is the portion of the cone 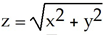 above the quarter disk
above the quarter disk 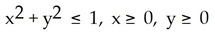 in the xy-plane.
in the xy-plane.A)
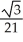
B)
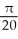
C)
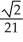
D)
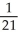
E) 0

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
69
Integrate f(x, y, z) = x + y + z over the surface of the cube cut from the first octant by the planes x = a, y = a, and z = a.
A) 8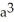
B) 9
C) 10
D) 11
E) 6
A) 8
B) 9
C) 10
D) 11
E) 6
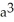

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
70
Integrate g(x, y, z) = x2y2z2 over the surface of the rectangular solid cut from the first octant by the planes x = a, y = b, and z = c.
A)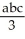 (ab + ac + bc)
(ab + ac + bc)
B)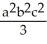 (ab + ac + bc)
(ab + ac + bc)
C)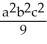 (ab + ac + bc)
(ab + ac + bc)
D)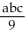 (ab + ac + bc)
(ab + ac + bc)
E) abc(ab + ac + bc)
A)
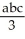 (ab + ac + bc)
(ab + ac + bc)B)
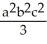 (ab + ac + bc)
(ab + ac + bc)C)
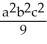 (ab + ac + bc)
(ab + ac + bc)D)
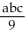 (ab + ac + bc)
(ab + ac + bc)E) abc(ab + ac + bc)

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
71
Find the value of the positive constant real number a such that the area of the part of the plane 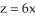 inside the elliptic paraboloid z = 3x2 + ay2 is equal to
inside the elliptic paraboloid z = 3x2 + ay2 is equal to 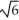 square units.
square units.
A)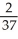
B)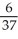
C)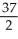
D)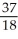
E)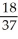
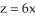 inside the elliptic paraboloid z = 3x2 + ay2 is equal to
inside the elliptic paraboloid z = 3x2 + ay2 is equal to 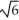 square units.
square units.A)
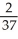
B)
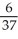
C)
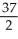
D)
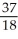
E)
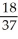

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
72
Find the area element at a point r (θ, φ) on the parametric surface 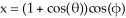 ,
, 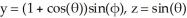 .
.
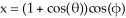 ,
, 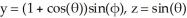 .
.
Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
73
Evaluate 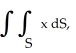 where S is the part of the paraboloid 2x = 8 -
where S is the part of the paraboloid 2x = 8 - 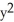 -
- 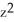 lying between the planes
lying between the planes 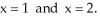
A) 2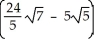
B) 2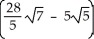
C) 2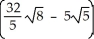
D)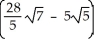
E)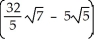
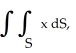 where S is the part of the paraboloid 2x = 8 -
where S is the part of the paraboloid 2x = 8 -  -
-  lying between the planes
lying between the planes 
A) 2
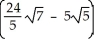
B) 2
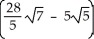
C) 2
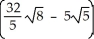
D)
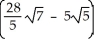
E)
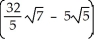

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
74
Find the surface area of the part of the cylinder x2 + y2 = 2y that lies in the first octant and under the paraboloid 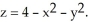
A) square units
B) 2 square units
C) 3 square units
D) 4 square units
E) 6 square units
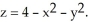
A) square units
B) 2 square units
C) 3 square units
D) 4 square units
E) 6 square units

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
75
Find the surface area of the part of the sphere x2 + y2 + z2 = 36 between the planes z = 1 and z = 5.
A) 12 square units
B) 288 square units
C) 48 square units
D) 96 square units
E) 144 square units
A) 12 square units
B) 288 square units
C) 48 square units
D) 96 square units
E) 144 square units

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
76
Find two unit vectors orthogonal to the parametric surface S given by r (u, v) = ( 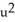 - 4
- 4 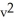 -
- 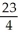 ) i + 4v j + 2u k at the point on the surface corresponding to (u, v) = ( 3 , -
) i + 4v j + 2u k at the point on the surface corresponding to (u, v) = ( 3 , -  ).
).
A) ±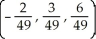
B) ± (- 1 , 0 ,0)
C) ±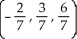
D) ±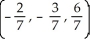
E) ±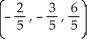
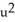 - 4
- 4 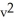 -
- 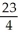 ) i + 4v j + 2u k at the point on the surface corresponding to (u, v) = ( 3 , -
) i + 4v j + 2u k at the point on the surface corresponding to (u, v) = ( 3 , -  ).
).A) ±
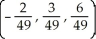
B) ± (- 1 , 0 ,0)
C) ±
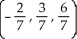
D) ±
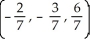
E) ±
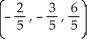

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
77
Compute the flux of F = x i + y j + z k upward through the part of the plane x + y + z = 3 in the first octant of 3-space.
A)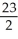
B)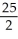
C)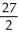
D)
E)
A)
B)
C)
D)
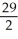
E)


Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
78
Compute the flux of F = x i + y j + z k outward through the whole surface of the tetrahedron bounded by the coordinate planes and the plane 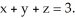
A)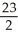
B)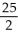
C)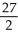
D)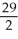
E) 0
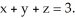
A)
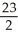
B)
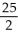
C)
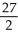
D)
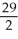
E) 0

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
79
Compute the flux of F = 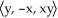 upward through the the part of the cone
upward through the the part of the cone 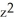 =
= 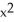 +
+ 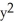 lying inside the first octant of cylinder
lying inside the first octant of cylinder 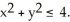
A) 1
B) 2
C) 4
D)
E)
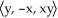 upward through the the part of the cone
upward through the the part of the cone  =
=  +
+  lying inside the first octant of cylinder
lying inside the first octant of cylinder 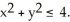
A) 1
B) 2
C) 4
D)

E)


Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
80
Compute the flux of F = 2x i - 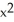 j + (z - 2x + 2y) k upward through the part of the plane
j + (z - 2x + 2y) k upward through the part of the plane 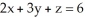 in the first octant of 3-space.
in the first octant of 3-space.
A)
B)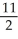
C)
D)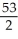
E) 0
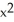 j + (z - 2x + 2y) k upward through the part of the plane
j + (z - 2x + 2y) k upward through the part of the plane 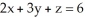 in the first octant of 3-space.
in the first octant of 3-space.A)

B)
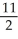
C)

D)
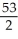
E) 0

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck


