Exam 16: Vector Fields
Exam 1: Preliminaries127 Questions
Exam 2: Limits and Continuity92 Questions
Exam 3: Differentiation131 Questions
Exam 4: Transcendental Functions129 Questions
Exam 5: More Applications of Differentiation130 Questions
Exam 6: Integration117 Questions
Exam 7: Techniques of Integration118 Questions
Exam 8: Applications of Integration139 Questions
Exam 9: Conics, Parametric Curves, and Polar Curves114 Questions
Exam 10: Sequences, Series, and Power Series125 Questions
Exam 11: Vectors and Coordinate Geometry in 3-Space119 Questions
Exam 12: Vector Functions and Curves87 Questions
Exam 13: Partial Differentiation104 Questions
Exam 14: Applications of Partial Derivatives67 Questions
Exam 15: Multiple Integration105 Questions
Exam 16: Vector Fields90 Questions
Exam 17: Vector Calculus92 Questions
Exam 18: Differential Forms and Exterior Calculus76 Questions
Exam 19: Ordinary Differential Equations135 Questions
Select questions type
Find the flux of F = xi + yj + zk upward through the hemisphere x2 + y2 + z2 = 1, z 0.
Free
(Multiple Choice)
4.8/5  (40)
(40)
Correct Answer:
A
Find two unit vectors orthogonal to the parametric surface S given by r (u, v) = ( 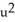 - 4
- 4 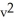 -
- 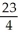 ) i + 4v j + 2u k at the point on the surface corresponding to (u, v) = ( 3 , -
) i + 4v j + 2u k at the point on the surface corresponding to (u, v) = ( 3 , -  ).
).
Free
(Multiple Choice)
4.8/5  (35)
(35)
Correct Answer:
C
Find the flux of the field F = (x + y) i + (y + z) j + (x + z)k outward across the surface of the cube 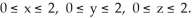
Free
(Multiple Choice)
4.8/5  (30)
(30)
Correct Answer:
B
The Liapunov function V(x,y) = 2 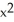 - xy + 3
- xy + 3 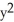 is suitable to confirm that the fixed point at the origin for the autonomous system
is suitable to confirm that the fixed point at the origin for the autonomous system 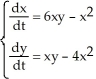 is at least stable.
is at least stable.
(True/False)
5.0/5  (35)
(35)
Find the work done by the force field F(x, y, z) = x i + 3xy j - (x + z) k on a particle moving along the line segment from (1, 4, 2) to (0, 5, 1).
(Multiple Choice)
4.9/5  (37)
(37)
Find 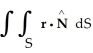 , where r = xi + yj + zk, over the entire surface of the cone with vertex at
, where r = xi + yj + zk, over the entire surface of the cone with vertex at 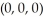 and base given by
and base given by 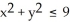 in the plane z = 5.
in the plane z = 5.
(Multiple Choice)
4.8/5  (35)
(35)
Evaluate the surface integral 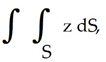 where S is the entire surface x + y + z = 1 lying in the first octant.
where S is the entire surface x + y + z = 1 lying in the first octant.
(Multiple Choice)
4.9/5  (43)
(43)
Let C be the curve of intersection of the paraboloid z = 6 - x2 - y2 and the cone z = 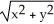 .Find the mass of the wire having the shape of the curve C if the line density function is given by
.Find the mass of the wire having the shape of the curve C if the line density function is given by 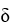 (x, y, z) = z
(x, y, z) = z 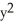 .
.
(Multiple Choice)
4.8/5  (39)
(39)
Integrate g(x, y, z) = x2y2z2 over the surface of the rectangular solid cut from the first octant by the planes x = a, y = b, and z = c.
(Multiple Choice)
4.9/5  (35)
(35)
Find the area of the ellipse cut from the plane z = cx by the cylinder 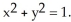 (c is constant.)
(c is constant.)
(Multiple Choice)
4.8/5  (28)
(28)
Show that the fixed point at the origin for the autonomous system 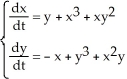 is unstable.
is unstable.
(Essay)
4.9/5  (40)
(40)
Evaluate the integral 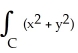 ds once around the square C in the xy-plane with vertices (± 1, 1) and (± 1, -1).
ds once around the square C in the xy-plane with vertices (± 1, 1) and (± 1, -1).
(Multiple Choice)
4.8/5  (43)
(43)
A potential function of a vector field F is given by 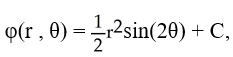 , where (r , θ) are the polar coordinates and C is an arbitrary constant. Find F.
Hint: The gradient of g(r , θ) is given by ∇g(r , θ) =
, where (r , θ) are the polar coordinates and C is an arbitrary constant. Find F.
Hint: The gradient of g(r , θ) is given by ∇g(r , θ) = 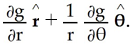 .
.
(Multiple Choice)
4.9/5  (27)
(27)
Compute the flux of F = x i + y j + z k upward through the part of the plane x + y + z = 3 in the first octant of 3-space.
(Multiple Choice)
4.7/5  (34)
(34)
Describe the streamlines of the given velocity field v(x, y, z) = - yi + xj.
(Multiple Choice)
4.8/5  (45)
(45)
Is F (x,y,z) = 6xy sin(2z) i + 3 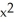 sin(2z) j - 6 xy cos(2z) k conservative? If so, find a potential for it.
sin(2z) j - 6 xy cos(2z) k conservative? If so, find a potential for it.
(Multiple Choice)
4.7/5  (37)
(37)
Evaluate the line integral 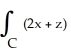 dx + 2y dy + (x + 2z) dz along the curve C with parametrization
dx + 2y dy + (x + 2z) dz along the curve C with parametrization 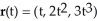 with
with 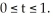
(Multiple Choice)
4.7/5  (35)
(35)
Find the work done by the conservative force F = (2y + z) i + (2x + z) j + (x + y) k in moving a particle along the elliptical helix 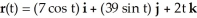 from
from 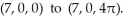
(Multiple Choice)
4.7/5  (38)
(38)
Find the family of field lines of the plane polar field F(r, ) = 2  +
+  .
.
(Multiple Choice)
4.8/5  (31)
(31)
Find a vector parametric equation of the field line of the vector field F(x, y, z) = -y i + x j + k that passes through the point (2, 0, 0).
(Multiple Choice)
4.8/5  (32)
(32)
Showing 1 - 20 of 90
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)