Deck 11: Vectors and Coordinate Geometry in 3-Space
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/119
Play
Full screen (f)
Deck 11: Vectors and Coordinate Geometry in 3-Space
1
Describe the surface with equation x2 + y2 + z2 - 6x + 2y - 12z = 75.
A) sphere with centre at (3, -1, 6) and radius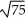
B) sphere with centre at (-3, 1, -6) and radius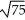
C) sphere with centre at (3, 1, 6) and radius 11
D) sphere with centre at (3, -1, 6) and radius 11
E) sphere with centre at (3, 1, 6) and radius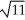
A) sphere with centre at (3, -1, 6) and radius
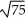
B) sphere with centre at (-3, 1, -6) and radius
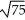
C) sphere with centre at (3, 1, 6) and radius 11
D) sphere with centre at (3, -1, 6) and radius 11
E) sphere with centre at (3, 1, 6) and radius
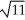
sphere with centre at (3, -1, 6) and radius 11
2
Find the distance between the points (x, y, z) and (2, 0, -3).
A)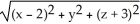
B)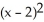 +
+ 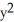 +
+ 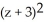
C)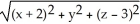
D)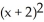 +
+ 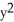 +
+ 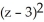
E)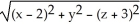
A)
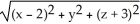
B)
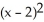 +
+ 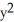 +
+ 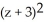
C)
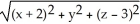
D)
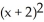 +
+ 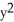 +
+ 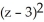
E)
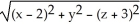
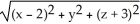
3
Find the distance between the points (2, 4, 7) and the (1, 5, 10).
A) 3
B)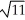
C)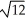
D)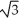
E) 11
A) 3
B)
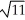
C)
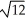
D)
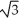
E) 11
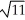
4
Find the distance between (2, -1, -2) and the origin.
A)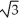
B)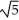
C) 3
D) 4
E) 9
A)
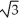
B)
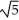
C) 3
D) 4
E) 9

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
5
Find the distance between (-2, 3, 1) and (4, 1, -3).
A)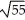
B) 2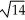
C)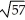
D)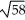
E) 2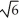
A)
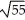
B) 2
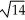
C)
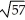
D)
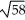
E) 2
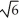

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
6
Find the equation of the sphere with radius 7 and centre (-1, 12, 9).
A)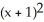 +
+ 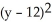 +
+ 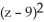 = 49
= 49
B)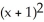 +
+ 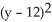 +
+ 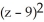 = 7
= 7
C)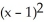 +
+ 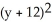 +
+ 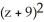 = 7
= 7
D)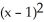 +
+ 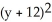 +
+ 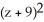 = 49
= 49
E)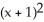 +
+ 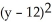 +
+ 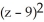 =
= 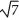
A)
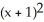 +
+ 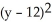 +
+ 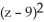 = 49
= 49B)
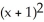 +
+ 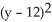 +
+ 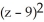 = 7
= 7C)
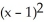 +
+ 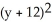 +
+ 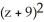 = 7
= 7D)
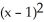 +
+ 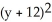 +
+ 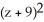 = 49
= 49E)
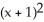 +
+ 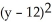 +
+ 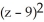 =
= 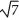

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
7
Describe the 3-space graph of the equation x2 + y2 = 0.
A) the xy-plane
B) the z-axis
C) a circle
D) a circular cylinder
E) a parabolic cylinder
A) the xy-plane
B) the z-axis
C) a circle
D) a circular cylinder
E) a parabolic cylinder

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
8
Describe the 3-space graph of the equation x2 + z2 = 4.
A) a circle of radius 2 in the xz-plane having centre at the origin
B) a circular cylinder of radius 2 with central axis along the y-axis
C) a sphere of radius 2 having centre at the origin
D) a disk of radius 2 in the xz-plane having centre at the origin.
E) a circular cylinder of radius 4 with central axis along the x-axis
A) a circle of radius 2 in the xz-plane having centre at the origin
B) a circular cylinder of radius 2 with central axis along the y-axis
C) a sphere of radius 2 having centre at the origin
D) a disk of radius 2 in the xz-plane having centre at the origin.
E) a circular cylinder of radius 4 with central axis along the x-axis

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
9
Describe the 3-space graph of the equation z2 = y2 + x2.
A) a surface of revolution obtained by rotating the parabola z = x2 in the xz-plane about the z-axis
B) a circular cone with vertex at the origin, axis along the z-axis, and semi-vertical angle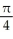
C) a circular cylinder with axis along the z-axis radius z
D) a circle having radius z in the xy-plane
E) a surface of revolution obtained by rotating the parabola z = y2 in the yz-plane about the z-axis
A) a surface of revolution obtained by rotating the parabola z = x2 in the xz-plane about the z-axis
B) a circular cone with vertex at the origin, axis along the z-axis, and semi-vertical angle
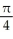
C) a circular cylinder with axis along the z-axis radius z
D) a circle having radius z in the xy-plane
E) a surface of revolution obtained by rotating the parabola z = y2 in the yz-plane about the z-axis

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
10
Describe the set of points in 3-space defined by the equations x2 + y2 + z2 - 8z = 9, x = 3.
A) a circle of radius 3 lying in the plane x = 3 and having centre at (3, 0, 4)
B) a circle of radius 3 lying in the plane x = 3 and having centre at (3, 0, -4)
C) a circle of radius 4 lying in the plane x = 3 and having centre at (3, 0, -4)
D) a circle of radius 4 lying in the plane x = 3 and having centre at (3, 0, 4)
E) a sphere of radius 5 having centre at (3, 0, 4)
A) a circle of radius 3 lying in the plane x = 3 and having centre at (3, 0, 4)
B) a circle of radius 3 lying in the plane x = 3 and having centre at (3, 0, -4)
C) a circle of radius 4 lying in the plane x = 3 and having centre at (3, 0, -4)
D) a circle of radius 4 lying in the plane x = 3 and having centre at (3, 0, 4)
E) a sphere of radius 5 having centre at (3, 0, 4)

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
11
If line L passes through point (1, 2, 3) and is perpendicular to the xy-plane, what are the coordinates of the points on the line that are at a distance 7 from the point P(3, -1, 5)?
A) (1, 2, 1) and (1, 2, 9)
B) (1, 2, 0) and (1, 2, 10)
C) (1, 2, -1) and (1, 2, 11)
D) (1, 2, -2) and (1, -2, 12)
E) (1, 2, -4) and (1, 2, 10)
A) (1, 2, 1) and (1, 2, 9)
B) (1, 2, 0) and (1, 2, 10)
C) (1, 2, -1) and (1, 2, 11)
D) (1, 2, -2) and (1, -2, 12)
E) (1, 2, -4) and (1, 2, 10)

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
12
Describe the intersection of the graphs of x2 + z2 = 4 and y = 2.
A) circle of radius 4 with centre at (0, 2, 0) in the plane z = 2
B) circle of radius 2 with centre at (0, 2, 0) in the plane y = 2
C) circle of radius 2 with centre at (0, -2, 0) in the plane y = -2
D) circle of radius 2 with centre at (1, 2, 1) in the plane y = 2
E) circle of radius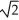 with centre at (0, 2, 0) in the plane y = 2
with centre at (0, 2, 0) in the plane y = 2
A) circle of radius 4 with centre at (0, 2, 0) in the plane z = 2
B) circle of radius 2 with centre at (0, 2, 0) in the plane y = 2
C) circle of radius 2 with centre at (0, -2, 0) in the plane y = -2
D) circle of radius 2 with centre at (1, 2, 1) in the plane y = 2
E) circle of radius
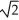 with centre at (0, 2, 0) in the plane y = 2
with centre at (0, 2, 0) in the plane y = 2
Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
13
Describe the intersection of the graphs of y = x and y = 5 in 3-space.
A) line through the point (5, 5, 0) and perpendicular to the xy-plane
B) line through the points (5, 5, 5) and (0, 0, 0)
C) line through the point (0, 5, 0) and perpendicular to the xy-plane
D) line through the points (5, 5, 0) and (0, 0, 0)
E) line through the points (0, 0, 0) and (5, 5, 0)
A) line through the point (5, 5, 0) and perpendicular to the xy-plane
B) line through the points (5, 5, 5) and (0, 0, 0)
C) line through the point (0, 5, 0) and perpendicular to the xy-plane
D) line through the points (5, 5, 0) and (0, 0, 0)
E) line through the points (0, 0, 0) and (5, 5, 0)

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
14
Describe the intersection of the graphs of y = x and y2 + z2 = 9.
A) the ellipse in which the vertical plane containing the z-axis and the point (1, 1, 0) intersects the horizontal circular cylinder of radius 3 with central axis along the x-axis
B) the circle in which the vertical plane containing the z-axis and the point (1, 1, 0) intersects the horizontal circular cylinder of radius 3 with central axis along the x-axis
C) the hyperbola in which the vertical plane containing the z-axis and the point (1, 1, 0) intersects the horizontal circular cylinder of radius 3 with central axis along the x-axis
D) the parabola in which the vertical plane containing the z-axis and the point (1, 1, 0) intersects the horizontal circular cylinder of radius 3 with central axis along the x-axis
E) the ellipse in which the vertical plane containing the z-axis and the point (1, 1, 0) intersects the horizontal circular cylinder of radius 3 with central axis along the y-axis
A) the ellipse in which the vertical plane containing the z-axis and the point (1, 1, 0) intersects the horizontal circular cylinder of radius 3 with central axis along the x-axis
B) the circle in which the vertical plane containing the z-axis and the point (1, 1, 0) intersects the horizontal circular cylinder of radius 3 with central axis along the x-axis
C) the hyperbola in which the vertical plane containing the z-axis and the point (1, 1, 0) intersects the horizontal circular cylinder of radius 3 with central axis along the x-axis
D) the parabola in which the vertical plane containing the z-axis and the point (1, 1, 0) intersects the horizontal circular cylinder of radius 3 with central axis along the x-axis
E) the ellipse in which the vertical plane containing the z-axis and the point (1, 1, 0) intersects the horizontal circular cylinder of radius 3 with central axis along the y-axis

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
15
Describe the intersection of the graphs of y = 3 and x2 + y2 = z2.
A) the parabola in which the vertical plane perpendicular to the y-axis and the point (0, 3, 0) intersects the right circular cone with axis along the x-axis and semi-vertical angle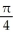
B) the circle in which the vertical plane perpendicular to the y-axis and the point (0, 3, 0) intersects the right circular cone with axis along the x-axis and semi-vertical angle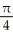
C) the hyperbola in which the vertical plane perpendicular to the y-axis and the point (0, 3, 0) intersects the right circular cone with axis along the x-axis and semi-vertical angle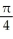
D) the ellipse in which the vertical plane perpendicular to the y-axis and the point (0, 3, 0) intersects the right circular cone with axis along the x-axis and semi-vertical angle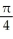
E) none of the above
A) the parabola in which the vertical plane perpendicular to the y-axis and the point (0, 3, 0) intersects the right circular cone with axis along the x-axis and semi-vertical angle
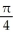
B) the circle in which the vertical plane perpendicular to the y-axis and the point (0, 3, 0) intersects the right circular cone with axis along the x-axis and semi-vertical angle
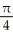
C) the hyperbola in which the vertical plane perpendicular to the y-axis and the point (0, 3, 0) intersects the right circular cone with axis along the x-axis and semi-vertical angle
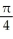
D) the ellipse in which the vertical plane perpendicular to the y-axis and the point (0, 3, 0) intersects the right circular cone with axis along the x-axis and semi-vertical angle
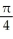
E) none of the above

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
16
Find an equation of the sphere with centre in the xz-plane and passing through the points(0, 8, 0), (4, 6, 2), and (0, 12, 4).
A) x2 + y2 + z2 - 14x + 24z = 257
B) x2 + y2 + z2 + 14x - 24z = 257
C) x2 + y2 + z2 - 14x + 24z = 64
D) x2 + y2 + z2 + 14x - 24z = 64
E) x2 + y2 + z2 - 14x - 24z = 257
A) x2 + y2 + z2 - 14x + 24z = 257
B) x2 + y2 + z2 + 14x - 24z = 257
C) x2 + y2 + z2 - 14x + 24z = 64
D) x2 + y2 + z2 + 14x - 24z = 64
E) x2 + y2 + z2 - 14x - 24z = 257

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
17
Find the point on the y-axis equidistant from (2, 5, -3) and (-3, 6, 1).
A) (0, -5, 0)
B) (0, 4, 0)
C) (0, 3, 2)
D) (0, -2, 0)
E) (0, -4, 0)
A) (0, -5, 0)
B) (0, 4, 0)
C) (0, 3, 2)
D) (0, -2, 0)
E) (0, -4, 0)

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
18
Find an equation describing all points that are equidistant from the points A(-3, 0, 4) and B(2, 1, 5). What does this equation describe geometrically?
A) 10x + 2y + 2z = 5, the plane that right bisects the line segment AB
B) 10x - 2y + 2z = 5, the plane that right bisects the line segment AB
C) 10x - 2y + 18z = 5, the plane that right bisects the line segment AB
D) 10x + 2y + 18z = 5, the plane that right bisects the line segment AB
E) 10x + 2y + 2z = 5, the plane that contains the points A and B
A) 10x + 2y + 2z = 5, the plane that right bisects the line segment AB
B) 10x - 2y + 2z = 5, the plane that right bisects the line segment AB
C) 10x - 2y + 18z = 5, the plane that right bisects the line segment AB
D) 10x + 2y + 18z = 5, the plane that right bisects the line segment AB
E) 10x + 2y + 2z = 5, the plane that contains the points A and B

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
19
When does the equation x2 + y2 + z2 + Ax + By + Cz + D = 0 represent a sphere?
A) if and only if A2 + B2 + C2 + D > 0
B) if and only if A2 + B2 - C2 > D
C) if and only if A2 - B2 + C2 > 0
D) if and only if A2 + B2 + C2 > 4D
E) if and only if A = 0, B = 0, C = 0, and D < 0
A) if and only if A2 + B2 + C2 + D > 0
B) if and only if A2 + B2 - C2 > D
C) if and only if A2 - B2 + C2 > 0
D) if and only if A2 + B2 + C2 > 4D
E) if and only if A = 0, B = 0, C = 0, and D < 0

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
20
There are fewer than two points on the graph of x2 + y2 + z2 + 2z + 2 = 0.

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
21
If v = -i + 7j and w = 4i - 4j, then find v + w.
A) 4i + 11j
B) 3i + 11j
C) 3i + 3j
D) 4i + 3j
E) 5i + 3j
A) 4i + 11j
B) 3i + 11j
C) 3i + 3j
D) 4i + 3j
E) 5i + 3j

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
22
Find the components of the unit vector in the same direction as v = 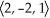 .
.
A)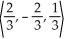
B)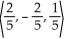
C)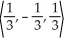
D)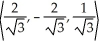
E)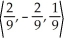
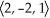 .
.A)
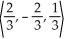
B)
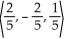
C)
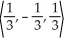
D)
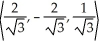
E)
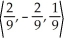

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
23
If v is a vector in the xy-plane, |v| = 7 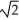 , and v makes an angle of 3 /4 with the positive direction of the x-axis, then what are the components of v?
, and v makes an angle of 3 /4 with the positive direction of the x-axis, then what are the components of v?
A)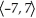
B)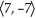
C)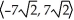
D)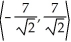
E)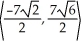
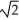 , and v makes an angle of 3 /4 with the positive direction of the x-axis, then what are the components of v?
, and v makes an angle of 3 /4 with the positive direction of the x-axis, then what are the components of v?A)
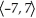
B)
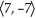
C)
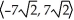
D)
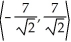
E)
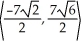

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
24
Find the length of the vector PQ where P = (1, -2, 4) and Q = (3, 4, 3).
A)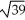
B) 2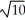
C)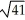
D)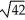
E)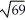
A)
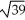
B) 2
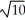
C)
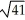
D)
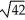
E)
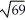

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
25
Find the angle between the vectors i + 2j - 3k and -i + 2j + k.
A)
B)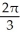
C)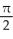
D)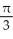
E)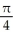
A)
B)
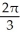
C)
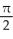
D)
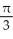
E)
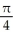

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
26
Find the angle between the vectors i + 2j + 3k and 2i - 3j - k.
A)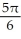
B)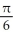
C)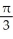
D)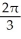
E)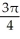
A)
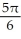
B)
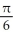
C)
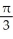
D)
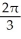
E)
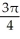

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
27
Find a value c for which A = 2i - j + 4k and B = i + cj + 8k will be perpendicular.
A) c = -18
B) c = -12
C) c = -34
D) c = 34
E) 0
A) c = -18
B) c = -12
C) c = -34
D) c = 34
E) 0

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
28
Find the vector of unit length in the direction opposite to that of v = 4i + 7j - 4k.
A) i +
i +  j -
j -  k
k
B) i +
i + 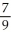 j -
j -  k
k
C) - i -
i -  j +
j +  k
k
D) - i -
i - 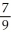 j +
j +  k
k
E) -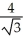 i -
i - 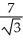 j +
j + 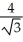 k
k
A)
 i +
i +  j -
j -  k
kB)
 i +
i + 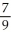 j -
j -  k
kC) -
 i -
i -  j +
j +  k
kD) -
 i -
i - 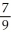 j +
j +  k
kE) -
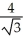 i -
i - 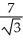 j +
j + 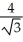 k
k
Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
29
Find the vector that makes equal acute angles with the positive coordinate axes and has length 2.
A)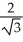 (i + j + k)
(i + j + k)
B) 2(i + j + k)
C)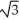 (i + j + k)
(i + j + k)
D)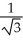 (i + j + k)
(i + j + k)
E)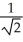 (i + j + k)
(i + j + k)
A)
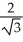 (i + j + k)
(i + j + k)B) 2(i + j + k)
C)
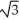 (i + j + k)
(i + j + k)D)
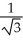 (i + j + k)
(i + j + k)E)
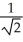 (i + j + k)
(i + j + k)
Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
30
Let u and v be non-zero vectors in 2 or 3-space. Find a simplified expression for 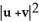 .
.
A)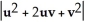
B)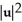 + 2
+ 2 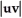 +
+ 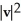
C)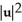 + 2
+ 2 
 +
+ 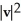
D)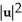 + 2
+ 2 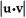 +
+ 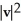
E)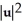 + 2u.v +
+ 2u.v + 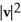
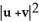 .
.A)
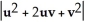
B)
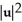 + 2
+ 2 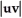 +
+ 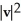
C)
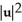 + 2
+ 2 
 +
+ 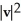
D)
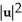 + 2
+ 2 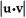 +
+ 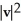
E)
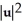 + 2u.v +
+ 2u.v + 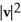

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
31
Find the scalar and vector projections of 2i -5j + k in the direction of 3i - 4k.
A) scalar 2, vector (3i - 4k)
(3i - 4k)
B) scalar , vector
, vector 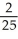 (3i - 4k)
(3i - 4k)
C) scalar , vector
, vector  (3i - 4k)
(3i - 4k)
D) scalar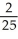 , vector
, vector 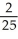 (3i - 4k)
(3i - 4k)
E) scalar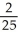 , vector
, vector  (3i - 4k)
(3i - 4k)
A) scalar 2, vector
 (3i - 4k)
(3i - 4k)B) scalar
 , vector
, vector 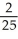 (3i - 4k)
(3i - 4k)C) scalar
 , vector
, vector  (3i - 4k)
(3i - 4k)D) scalar
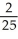 , vector
, vector 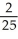 (3i - 4k)
(3i - 4k)E) scalar
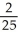 , vector
, vector  (3i - 4k)
(3i - 4k)
Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
32
A vector in 100-dimensional Euclidean space R100 makes equal acute angles with the positive directions of the 100 coordinate axes. Approximately what is that angle?
A) 68.71°
B) 84.26°
C) 75.44°
D) 87.18°
E) 45.00°
A) 68.71°
B) 84.26°
C) 75.44°
D) 87.18°
E) 45.00°

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
33
Given u = i - 2j + k and v = 3i + j - 2k, find each of the following:
(a) u x v, (b) v x u, and (c) v x v.
(a) u x v, (b) v x u, and (c) v x v.

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
34
Given u = i - 2j + k and v = 3i + j - 2k, find each of the following:(a) u x v, (b) v x u, and (c) v x v.
A) (a) 3i + 5j + 7k, (b) -3i - 5j - 7k, (c) 0
B) (a) 3i - 5j + 7k, (b) -3i + 5j - 7k, (c) -4i +12j
C) (a) 3i + 5j - 5k, (b) -3i - 5j + 5k, (c) 12j
D) (a) 3i - 5j - 5k, (b) -3i + 5j + 5k, (c) -4 i + 6k
E) (a) 3i + 5j + 7k, (b) -3i - 5j - 5k, (c) 0
A) (a) 3i + 5j + 7k, (b) -3i - 5j - 7k, (c) 0
B) (a) 3i - 5j + 7k, (b) -3i + 5j - 7k, (c) -4i +12j
C) (a) 3i + 5j - 5k, (b) -3i - 5j + 5k, (c) 12j
D) (a) 3i - 5j - 5k, (b) -3i + 5j + 5k, (c) -4 i + 6k
E) (a) 3i + 5j + 7k, (b) -3i - 5j - 5k, (c) 0

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
35
Calculate u × v where u = 2i + j - k and v = -3i + 4j + k.
A) 5i + j - 11k
B) 5i - j + 11k
C) 5i + j + 11k
D) -5i + j + 11k
E) -5i + j - 11k
A) 5i + j - 11k
B) 5i - j + 11k
C) 5i + j + 11k
D) -5i + j + 11k
E) -5i + j - 11k

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
36
If u = 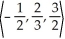 and v =
and v = 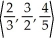 , evaluate u x v.
, evaluate u x v.
A)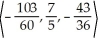
B)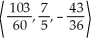
C)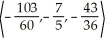
D)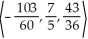
E)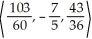
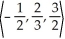 and v =
and v = 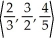 , evaluate u x v.
, evaluate u x v.A)
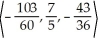
B)
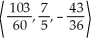
C)
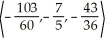
D)
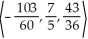
E)
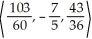

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
37
Given u = 2i - j + 2k and v = i - j + 4k, find each of the following:(a) u × v, (b) v × u, and (c) v × v.
A) (a) -2i - 6j - k, (b) 2i + 6j + k, (c) 0
B) (a) -2i - 6j - k, (b) -2i - 6j - k, (c) -4i +8j -4k
C) (a) 2i + 6j + k, (b) -2i - 6j - k, (c) -4i +8j -4k
D) (a) -2i - 6j + k, (b) 2i + 6j - k, (c) 0
E) (a) -2i + 6j - k, (b) 2i - 6j + k, (c) 0
A) (a) -2i - 6j - k, (b) 2i + 6j + k, (c) 0
B) (a) -2i - 6j - k, (b) -2i - 6j - k, (c) -4i +8j -4k
C) (a) 2i + 6j + k, (b) -2i - 6j - k, (c) -4i +8j -4k
D) (a) -2i - 6j + k, (b) 2i + 6j - k, (c) 0
E) (a) -2i + 6j - k, (b) 2i - 6j + k, (c) 0

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
38
Find the area of a triangle that has vertices (4, 3, 6), (-2, 0, 8), (1, 5, 0).
A)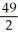 square units
square units
B) 49 square units
C)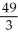 square units
square units
D)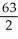 square units
square units
E) 28 square units
A)
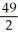 square units
square unitsB) 49 square units
C)
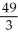 square units
square unitsD)
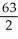 square units
square unitsE) 28 square units

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
39
Find the two unit vectors orthogonal to both a = 3j + 2k and b = - i - 2k.
A) - i -
i -  j +
j +  k and
k and  i +
i +  j -
j -  k
k
B) k and -k
C) - i +
i +  j and
j and  i -
i -  j
j
D) - i +
i +  j +
j +  k and
k and  i -
i -  j -
j -  k
k
E) -6i - 2j + 3k and 6i + 2j - 3k
A) -
 i -
i -  j +
j +  k and
k and  i +
i +  j -
j -  k
kB) k and -k
C) -
 i +
i +  j and
j and  i -
i -  j
jD) -
 i +
i +  j +
j +  k and
k and  i -
i -  j -
j -  k
kE) -6i - 2j + 3k and 6i + 2j - 3k

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
40
If u = 3i + j + 4k, v = -i + 2j, and w = - 2i - 3j + 5k, evaluate u × (3v - w).
A) 41i + 11j + 28k
B) 41i - 11j + 28k
C) -41i - 11j + 28k
D) -41i + 11j + 28k
E) 41i - 11j - 28k
A) 41i + 11j + 28k
B) 41i - 11j + 28k
C) -41i - 11j + 28k
D) -41i + 11j + 28k
E) 41i - 11j - 28k

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
41
If u = 3i + j + 4k, v = -i + 2j, and w = - 2i - 3j + 5k, evaluate u × (v × w).
A) -13i + 19j + 5k
B) -14i + 20j + 4k
C) -13i - 19j - 5k
D) 14i - 20j - 4k
E) 13i - 19j - 5k
A) -13i + 19j + 5k
B) -14i + 20j + 4k
C) -13i - 19j - 5k
D) 14i - 20j - 4k
E) 13i - 19j - 5k

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
42
If u = 3i + j + 4k, v = -i + 2j, and w = - 2i - 3j + 5k, evaluate u . (v × w).
A) 63
B) 64
C) -64
D) 62
E) -63
A) 63
B) 64
C) -64
D) 62
E) -63

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
43
If u, v, and w are vectors in 3-space and u × v = u × w, then v = w.

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
44
u × (v × w) = (u × v) × w for all vectors u, v, and w in 3-space.

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
45
Find the volume of a parallelepiped spanned by vectors from the origin to the three points (1, 1, -3), (-1, 3, -1), and (3, 5, 7).
A) 70 cubic units
B) 72 cubic units
C) 68 cubic units
D) 76 cubic units
E) 11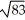 cubic units
cubic units
A) 70 cubic units
B) 72 cubic units
C) 68 cubic units
D) 76 cubic units
E) 11
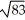 cubic units
cubic units
Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
46
Find the volume of the tetrahedron spanned by the vectors u = 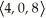 , v =
, v = 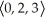 , and w =
, and w = 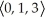 .
.
A) 2 cubic units
B) 3 cubic units
C) 4 cubic units
D) 5 cubic units
E) 1 cubic unit
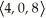 , v =
, v = 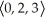 , and w =
, and w = 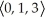 .
.A) 2 cubic units
B) 3 cubic units
C) 4 cubic units
D) 5 cubic units
E) 1 cubic unit

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
47
A force F of magnitude 6 N acts in the direction of the vector i + 2j- 2k and is applied at the point 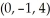 . (Distances are in centimetres.) What is the magnitude of the torque of F about the point
. (Distances are in centimetres.) What is the magnitude of the torque of F about the point 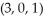 ?
?
A) 14 N . cm
B) 5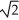 N . cm
N . cm
C) 10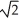 N . cm
N . cm
D) 15 N . cm
E) 30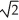 N . cm
N . cm
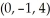 . (Distances are in centimetres.) What is the magnitude of the torque of F about the point
. (Distances are in centimetres.) What is the magnitude of the torque of F about the point 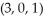 ?
?A) 14 N . cm
B) 5
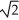 N . cm
N . cmC) 10
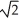 N . cm
N . cmD) 15 N . cm
E) 30
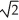 N . cm
N . cm
Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
48
Given three vectors u, v, and w, with v and w not 0 or parallel, find the vector projection of u in the plane containing the origin and the points represented by the position vectors v and w.
A) -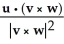 (v × w)
(v × w)
B)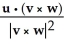 (v × w) - u
(v × w) - u
C) u -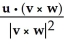 (v × w)
(v × w)
D)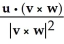 (v × w)
(v × w)
E) none of the above
A) -
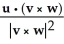 (v × w)
(v × w)B)
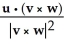 (v × w) - u
(v × w) - uC) u -
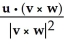 (v × w)
(v × w)D)
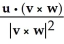 (v × w)
(v × w)E) none of the above

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
49
If u × v = 0 (the zero vector), then either u = 0 or v = 0.

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
50
Write standard form equations for the line through the point (1, 2, -6) and parallel to the vector 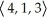 .
.
A)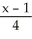 =
= 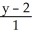 =
= 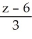
B)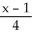 =
= 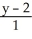 =
= 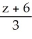
C)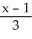 =
= 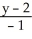 =
= 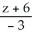
D)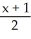 =
= 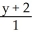 =
= 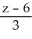
E)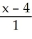 =
= 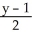 = -
= - 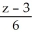
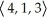 .
.A)
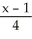 =
= 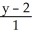 =
= 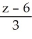
B)
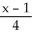 =
= 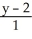 =
= 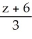
C)
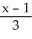 =
= 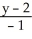 =
= 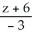
D)
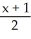 =
= 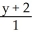 =
= 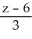
E)
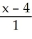 =
= 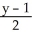 = -
= - 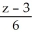

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
51
The planes x + 2y - 4z = 10 and -2x - 4y - 8z = 11 are parallel.

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
52
Find the cosine of the angle between the planes 3x + 3y - 6z = 12 and 7x - 5y + 2z = -8.
A) ±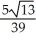
B) ±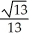
C) ±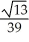
D) ±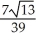
E) ±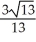
A) ±
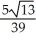
B) ±
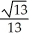
C) ±
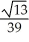
D) ±
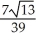
E) ±
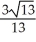

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
53
Find the equation for the plane that passes through the point (1, 2, 3) and is normal to the vector joining (1, 3, 2) and (2, 3, 1).
A) x - z + 2 = 0
B) x + z +2 = 0
C) 2x - z +1 = 0
D) x - 2z -1 = 0
E) x + z -2= 0
A) x - z + 2 = 0
B) x + z +2 = 0
C) 2x - z +1 = 0
D) x - 2z -1 = 0
E) x + z -2= 0

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
54
Find the equation of a plane containing the point (2, -4, 3) and the line 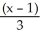 =
= 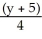 = z + 2.
= z + 2.
A) 19x + 14y - z = -21
B) 19x - 14y - z = 91
C) 19x - 14y + z = 97
D) 19x + 14y + z = -15
E) 19x + 14y - 2z = 91
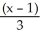 =
= 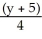 = z + 2.
= z + 2.A) 19x + 14y - z = -21
B) 19x - 14y - z = 91
C) 19x - 14y + z = 97
D) 19x + 14y + z = -15
E) 19x + 14y - 2z = 91

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
55
Find the equation of the straight line passing through the point (1, 2, -3) and is perpendicular to the plane 3x - 7y +4z - 17 = 0.
A) r = (1 + 3t) i + (2 - 7t) j + (- 3 + 4t) k, t (- , )
(- , )
B) 3x - 7y + 4z - 23 = 0
C) r = (3 + t) i + (- 7 + 2t) j + (4 - 3t) k, t 11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 (- , )
D) x + y + z = 0
E)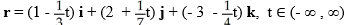
A) r = (1 + 3t) i + (2 - 7t) j + (- 3 + 4t) k, t
 (- , )
(- , )B) 3x - 7y + 4z - 23 = 0
C) r = (3 + t) i + (- 7 + 2t) j + (4 - 3t) k, t 11ee7b17_3372_5854_ae82_d19d2ea0c252_TB9661_11 (- , )
D) x + y + z = 0
E)
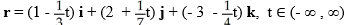

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
56
Find the acute angle between the planes with equations
x + y -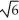 z = 3 and x + y +
z = 3 and x + y + 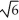 z = 5.
z = 5.
A)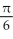
B)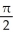
C)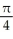
D)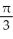
E)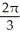
x + y -
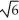 z = 3 and x + y +
z = 3 and x + y + 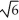 z = 5.
z = 5.A)
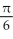
B)
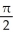
C)
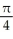
D)
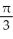
E)
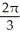

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
57
Find the distance from the point P(1, -1, 2) to the line connecting the point (3, 1, 4) to (1, -3, 0).
A)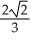 units
units
B)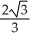 units
units
C) units
units
D) units
units
E)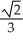 units
units
A)
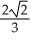 units
unitsB)
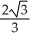 units
unitsC)
 units
unitsD)
 units
unitsE)
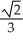 units
units
Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
58
Find parametric equations of the straight line containing the point (2, 1, -4) and is parallel to the line of intersection of the planes 3x +2y - z = 0 and x + y + z = -9.

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
59
Find the distance between the lines  =
= 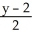 =
= 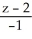 and
and 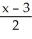 =
= 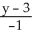 =
= 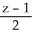 .
.
A)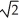 units
units
B) 3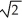 units
units
C) 2 units
D) 3 units
E) 1 unit
 =
= 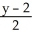 =
= 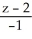 and
and 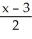 =
= 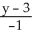 =
= 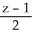 .
.A)
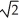 units
unitsB) 3
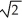 units
unitsC) 2 units
D) 3 units
E) 1 unit

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
60
Find the equation of a plane that contains the line 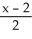 =
= 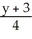 =
= 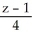 and is parallel to the plane 2x - 3y + 2z = 0.
and is parallel to the plane 2x - 3y + 2z = 0.
A) 2x - 3y + 2z = 15
B) 2x - 3y + 2z = -15
C) 2x - 3y + 2z = 12
D) 2x - 3y + 2z = -12
E) 2x + 3y + 2z = 15
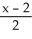 =
= 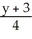 =
= 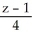 and is parallel to the plane 2x - 3y + 2z = 0.
and is parallel to the plane 2x - 3y + 2z = 0.A) 2x - 3y + 2z = 15
B) 2x - 3y + 2z = -15
C) 2x - 3y + 2z = 12
D) 2x - 3y + 2z = -12
E) 2x + 3y + 2z = 15

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
61
Find the equation of a plane that contains the lines= 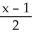
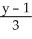 =
= 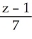 and
and 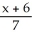 -
- 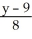 == z - 2.
== z - 2.
A) 53x + 51y - 37z = 67
B) 53x - 47y + 5z = -731
C) 53x - 47y +57 = 11
D) 53x + 51y - 37z = -67
E) 53x - 47y - 5z = 11
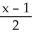
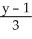 =
= 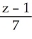 and
and 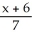 -
- 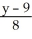 == z - 2.
== z - 2.A) 53x + 51y - 37z = 67
B) 53x - 47y + 5z = -731
C) 53x - 47y +57 = 11
D) 53x + 51y - 37z = -67
E) 53x - 47y - 5z = 11

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
62
For what values of the constants k and c does the line 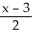 =
=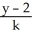 =
= 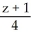 lie in the plane x - y + 2z = c?
lie in the plane x - y + 2z = c?
A) k = -10, c = 1
B) k = 10, c = 0
C) k = 10, c = -1
D) k = -8, c = 2
E) k = -2, c = 0
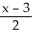 =
=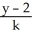 =
= 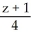 lie in the plane x - y + 2z = c?
lie in the plane x - y + 2z = c?A) k = -10, c = 1
B) k = 10, c = 0
C) k = 10, c = -1
D) k = -8, c = 2
E) k = -2, c = 0

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
63
For what value of the constant k will the vectors 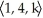 ,
, 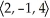 , and
, and 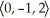 be coplanar?
be coplanar?
A) k = 8
B) k = -7
C) k = 6
D) k = -5
E) k = 0
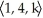 ,
, 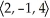 , and
, and 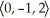 be coplanar?
be coplanar?A) k = 8
B) k = -7
C) k = 6
D) k = -5
E) k = 0

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
64
The distance from the point (2, -1, -2) to the plane 6x + 2y - 3z + a = 0 is 2 units. Find a.
A) 2
B) -2 or -30
C) -14
D) -10 or -22
E) -14, -18
A) 2
B) -2 or -30
C) -14
D) -10 or -22
E) -14, -18

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
65
A plane in 3-space is uniquely determined by any three different points that lie on it.

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
66
Consider the straight line L: 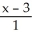 =
= 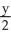 =
= 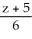
(i) Find the point on the line L closest to the point P (-2, -1, 3).
(ii) Find the shortest distance from the point P to the line L.
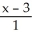 =
= 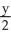 =
= 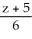
(i) Find the point on the line L closest to the point P (-2, -1, 3).
(ii) Find the shortest distance from the point P to the line L.

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
67
Find the coordinates of the point where the line that passes through the point (0, -3, 8) and is parallel to the line given by x = 10 + 3t, y = 12t, and z = -3 - t intersects the xz-plane.
A)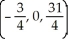
B)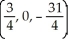
C)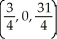
D)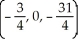
E)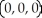
A)
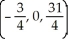
B)
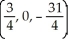
C)
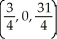
D)
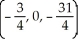
E)
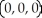

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
68
Determine the equation of the plane that contains the points P = (1, -2, 0), Q = (3, 1, 4), and R = (0, -1, 2).
A) 2x - 8y + 5z = 18
B) 2x + 8y + 5z = -14
C) 2x + 8y - 5z = -14
D) 2x - 8y - 5z = 18
E) 2x + 8y + 5z = 18
A) 2x - 8y + 5z = 18
B) 2x + 8y + 5z = -14
C) 2x + 8y - 5z = -14
D) 2x - 8y - 5z = 18
E) 2x + 8y + 5z = 18

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
69
Describe the graph of 9x2 - y2 + 16z2 = 144.
A) a hyperboloid of one sheet
B) a hyperboloid of two sheets
C) a hyperbolic paraboloid
D) an elliptic paraboloid
E) an ellipsoid (or a sphere)
F) a cylinder (circular, elliptic, parabolic, or hyperbolic)
G) a cone (circular, elliptic, parabolic, or hyperbolic)
H) none of the above
A) a hyperboloid of one sheet
B) a hyperboloid of two sheets
C) a hyperbolic paraboloid
D) an elliptic paraboloid
E) an ellipsoid (or a sphere)
F) a cylinder (circular, elliptic, parabolic, or hyperbolic)
G) a cone (circular, elliptic, parabolic, or hyperbolic)
H) none of the above

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
70
Describe the graph of 25x2 - y2 - z2 = 25.
A) a hyperboloid of one sheet
B) a hyperboloid of two sheets
C) a hyperbolic paraboloid
D) an elliptic paraboloid
E) an ellipsoid (or a sphere)
F) a cylinder (circular, elliptic, parabolic, or hyperbolic)
G) a cone (circular, elliptic, parabolic, or hyperbolic)
H) none of the above
A) a hyperboloid of one sheet
B) a hyperboloid of two sheets
C) a hyperbolic paraboloid
D) an elliptic paraboloid
E) an ellipsoid (or a sphere)
F) a cylinder (circular, elliptic, parabolic, or hyperbolic)
G) a cone (circular, elliptic, parabolic, or hyperbolic)
H) none of the above

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
71
Which of the following equations is an equation of a circular cone?
A) z2 = 1 + 4x2 + 4y2
B) z = x2 + y2 + z2
C) z = 1 + x2 + y2
D) x2 + z2 = 1
E) z2 = 4(x2 + y2)
A) z2 = 1 + 4x2 + 4y2
B) z = x2 + y2 + z2
C) z = 1 + x2 + y2
D) x2 + z2 = 1
E) z2 = 4(x2 + y2)

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
72
Which of the following equations is an equation of a hyperboloid of one sheet?
A) x2 + y2 - z2 = 0
B) x2 - y2 - z2 + 1= 0
C) x2 + y2 - z2 + 1= 0
D) z2 = x2 - y2
E) 2x2 - y + 3z2 = 1
A) x2 + y2 - z2 = 0
B) x2 - y2 - z2 + 1= 0
C) x2 + y2 - z2 + 1= 0
D) z2 = x2 - y2
E) 2x2 - y + 3z2 = 1

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
73
Describe the graph of x2 + 4z2 = 2y.
A) a hyperboloid of one sheet
B) a hyperboloid of two sheets
C) a hyperbolic paraboloid
D) an elliptic paraboloid
E) an ellipsoid (or a sphere)
F) a cylinder (circular, elliptic, parabolic, or hyperbolic)
G) a cone (circular, elliptic, parabolic, or hyperbolic)
H) none of the above
A) a hyperboloid of one sheet
B) a hyperboloid of two sheets
C) a hyperbolic paraboloid
D) an elliptic paraboloid
E) an ellipsoid (or a sphere)
F) a cylinder (circular, elliptic, parabolic, or hyperbolic)
G) a cone (circular, elliptic, parabolic, or hyperbolic)
H) none of the above

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
74
Describe the graph of 4x2 - y2 = 2x + 3y.
A) a hyperboloid of one sheet
B) a hyperboloid of two sheets
C) a hyperbolic paraboloid
D) an elliptic paraboloid
E) an ellipsoid (or a sphere)
F) a cylinder (circular, elliptic, parabolic, or hyperbolic)
G) a cone (circular, elliptic, parabolic, or hyperbolic)
H) none of the above
A) a hyperboloid of one sheet
B) a hyperboloid of two sheets
C) a hyperbolic paraboloid
D) an elliptic paraboloid
E) an ellipsoid (or a sphere)
F) a cylinder (circular, elliptic, parabolic, or hyperbolic)
G) a cone (circular, elliptic, parabolic, or hyperbolic)
H) none of the above

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
75
Describe the graph of x2 + 4y2 + 16z2 = 2x - 8y.
A) a hyperboloid of one sheet
B) a hyperboloid of two sheets
C) a hyperbolic paraboloid
D) an elliptic paraboloid
E) an ellipsoid (or a sphere)
F) a cylinder (circular, elliptic, parabolic, or hyperbolic)
G) a cone (circular, elliptic, parabolic, or hyperbolic)
H) none of the above
A) a hyperboloid of one sheet
B) a hyperboloid of two sheets
C) a hyperbolic paraboloid
D) an elliptic paraboloid
E) an ellipsoid (or a sphere)
F) a cylinder (circular, elliptic, parabolic, or hyperbolic)
G) a cone (circular, elliptic, parabolic, or hyperbolic)
H) none of the above

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
76
Which of the following is an equation of a hyperboloid of two sheets?
A) x2 + y2 - z2 = 0
B) x2 - y2 - z2 = -1
C) z2 = 1 - x2 - y2
D) x2 + y2 + 1 = z2
E) z = - x2 - y2
A) x2 + y2 - z2 = 0
B) x2 - y2 - z2 = -1
C) z2 = 1 - x2 - y2
D) x2 + y2 + 1 = z2
E) z = - x2 - y2

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
77
Describe the set of points in 3-space satisfying z2 = x2 + y2 and z = x + y.
A) two straight lines
B) one straight line
C) an ellipse
D) a parabola
E) a hyperbola
F) none of the above
A) two straight lines
B) one straight line
C) an ellipse
D) a parabola
E) a hyperbola
F) none of the above

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
78
Describe the set of points in 3-space satisfying z2 = x2 + y2 and z = 2x.
A) two straight lines
B) one straight line
C) an ellipse
D) a parabola
E) a hyperbola
F) none of the above
A) two straight lines
B) one straight line
C) an ellipse
D) a parabola
E) a hyperbola
F) none of the above

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
79
Describe the set of points in 3-space satisfying z2 = x2 + y2 and z = 1 + y.
A) two straight lines
B) one straight line
C) an ellipse (or a circle)
D) a parabola
E) a hyperbola
F) none of the above
A) two straight lines
B) one straight line
C) an ellipse (or a circle)
D) a parabola
E) a hyperbola
F) none of the above

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck
80
Describe the set of points in 3-space satisfying x2 + 2y2 + 3z2 = 4 and z = x + y.
A) two straight lines
B) one straight line
C) an ellipse
D) a parabola
E) a hyperbola
F) none of the above
A) two straight lines
B) one straight line
C) an ellipse
D) a parabola
E) a hyperbola
F) none of the above

Unlock Deck
Unlock for access to all 119 flashcards in this deck.
Unlock Deck
k this deck


