Exam 11: Vectors and Coordinate Geometry in 3-Space
Exam 1: Preliminaries127 Questions
Exam 2: Limits and Continuity92 Questions
Exam 3: Differentiation131 Questions
Exam 4: Transcendental Functions129 Questions
Exam 5: More Applications of Differentiation130 Questions
Exam 6: Integration117 Questions
Exam 7: Techniques of Integration118 Questions
Exam 8: Applications of Integration139 Questions
Exam 9: Conics, Parametric Curves, and Polar Curves114 Questions
Exam 10: Sequences, Series, and Power Series125 Questions
Exam 11: Vectors and Coordinate Geometry in 3-Space119 Questions
Exam 12: Vector Functions and Curves87 Questions
Exam 13: Partial Differentiation104 Questions
Exam 14: Applications of Partial Derivatives67 Questions
Exam 15: Multiple Integration105 Questions
Exam 16: Vector Fields90 Questions
Exam 17: Vector Calculus92 Questions
Exam 18: Differential Forms and Exterior Calculus76 Questions
Exam 19: Ordinary Differential Equations135 Questions
Select questions type
Describe the set of points in 3-space satisfying z2 = 1 + x2 + 2y2 and z = y.
Free
(Multiple Choice)
4.9/5  (31)
(31)
Correct Answer:
F
Find the equation of a plane that contains the lines= 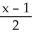
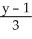 =
= 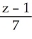 and
and 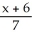 -
- 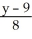 == z - 2.
== z - 2.
Free
(Multiple Choice)
4.8/5  (30)
(30)
Correct Answer:
A
A plane in 3-space is uniquely determined by any three different points that lie on it.
Free
(True/False)
4.9/5  (36)
(36)
Correct Answer:
False
Find the distance from the point P(1, -1, 2) to the line connecting the point (3, 1, 4) to (1, -3, 0).
(Multiple Choice)
4.8/5  (37)
(37)
Given u = i - 2j + k and v = 3i + j - 2k, find each of the following:(a) u x v, (b) v x u, and (c) v x v.
(Multiple Choice)
4.8/5  (37)
(37)
If u = 3i + j + 4k, v = -i + 2j, and w = - 2i - 3j + 5k, evaluate u × (v × w).
(Multiple Choice)
4.7/5  (35)
(35)
Find the equation of the line of intersection of the planes 2x + 6y - z - 19 = 0,x + 3 y - 3z = 2.
(Multiple Choice)
4.8/5  (34)
(34)
If line L passes through point (1, 2, 3) and is perpendicular to the xy-plane, what are the coordinates of the points on the line that are at a distance 7 from the point P(3, -1, 5)?
(Multiple Choice)
4.9/5  (41)
(41)
Given u = 2i - j + 2k and v = i - j + 4k, find each of the following:(a) u × v, (b) v × u, and (c) v × v.
(Multiple Choice)
4.9/5  (39)
(39)
For what value of the constant k will the vectors 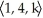 ,
, 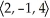 , and
, and 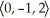 be coplanar?
be coplanar?
(Multiple Choice)
4.9/5  (40)
(40)
Find the eigenvalues and corresponding eigenvectors of the matrix A =  .
.
(Multiple Choice)
4.8/5  (34)
(34)
If v is a vector in the xy-plane, |v| = 7 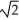 , and v makes an angle of 3 /4 with the positive direction of the x-axis, then what are the components of v?
, and v makes an angle of 3 /4 with the positive direction of the x-axis, then what are the components of v?
(Multiple Choice)
4.9/5  (44)
(44)
If u = 3i + j + 4k, v = -i + 2j, and w = - 2i - 3j + 5k, evaluate u . (v × w).
(Multiple Choice)
4.8/5  (39)
(39)
Find the vector that makes equal acute angles with the positive coordinate axes and has length 2.
(Multiple Choice)
4.8/5  (34)
(34)
The planes x + 2y - 4z = 10 and -2x - 4y - 8z = 11 are parallel.
(True/False)
4.9/5  (31)
(31)
Use Maple or other computer algebra software to classify the symmetric matrix A = 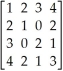 as positive or negative definite, positive or negative semidefinite, or indefinite.
as positive or negative definite, positive or negative semidefinite, or indefinite.
(Multiple Choice)
4.9/5  (45)
(45)
Showing 1 - 20 of 119
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)