Deck 10: Managing Customer and Work Flows
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/50
Play
Full screen (f)
Deck 10: Managing Customer and Work Flows
1
Leyland Motors can service an average 5 cars per hour, and the owner of Leyland Motors wants to know the probability of various customer arrival rates. Given the average arrival rate of 4 customers per hour, the owner uses the Poisson distribution to calculate the probabilities of various customer arrivals per hour.
-What is the probability of exactly 2 customers arriving within 1 hour?
A)0.0183
B)0.0733
C)0.1465
D)0.1954
E)0.1563
-What is the probability of exactly 2 customers arriving within 1 hour?
A)0.0183
B)0.0733
C)0.1465
D)0.1954
E)0.1563
0.1465
2
Leyland Motors can service an average 5 cars per hour, and the owner of Leyland Motors wants to know the probability of various customer arrival rates. Given the average arrival rate of 4 customers per hour, the owner uses the Poisson distribution to calculate the probabilities of various customer arrivals per hour.
-What is the probability of exactly 5 customers arriving within 1 hour?
A)0.0183
B)0.0733
C)0.1465
D)0.1954
E)0.1563
-What is the probability of exactly 5 customers arriving within 1 hour?
A)0.0183
B)0.0733
C)0.1465
D)0.1954
E)0.1563
0.1563
3
Leyland Motors can service an average 5 cars per hour, and the owner of Leyland Motors wants to know the probability of various customer arrival rates. Given the average arrival rate of 4 customers per hour, the owner uses the Poisson distribution to calculate the probabilities of various customer arrivals per hour.
-What is the probability that none of the customers will arrive within 1 hour?
A)0.0183
B)0.0733
C)0.1465
D)0.1954
E)0.1563
-What is the probability that none of the customers will arrive within 1 hour?
A)0.0183
B)0.0733
C)0.1465
D)0.1954
E)0.1563
0.0183
4
Leyland Motors can service an average 5 cars per hour, and the owner of Leyland Motors wants to know the probability of various customer arrival rates. Given the average arrival rate of 4 customers per hour, the owner uses the Poisson distribution to calculate the probabilities of various customer arrivals per hour.
-What is the probability that at least 2 of the customers will arrive within 1 hour?
A)0.0183
B)0.0733
C)0.1465
D)0.9084
E)0.0916
-What is the probability that at least 2 of the customers will arrive within 1 hour?
A)0.0183
B)0.0733
C)0.1465
D)0.9084
E)0.0916

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
5
Leyland Motors can service an average 5 cars per hour, and the owner of Leyland Motors wants to know the probability of various customer arrival rates. Given the average arrival rate of 4 customers per hour, the owner uses the Poisson distribution to calculate the probabilities of various customer arrivals per hour.
-What is the probability that, at most, 3 of the customers will arrive within 1 hour?
A)0.2381
B)0.4335
C)0.5665
D)0.1954
E)0.7619
-What is the probability that, at most, 3 of the customers will arrive within 1 hour?
A)0.2381
B)0.4335
C)0.5665
D)0.1954
E)0.7619

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
6
Leyland Motors can service an average 5 cars per hour, and the owner of Leyland Motors wants to know the probability of various customer arrival rates. Given the average arrival rate of 4 customers per hour, the owner uses the Poisson distribution to calculate the probabilities of various customer arrivals per hour.
-What is the probability that there will be more than 5 customers arriving within 1 hour?
A)0.1954
B)0.6288
C)0.2149
D)0.1563
E)0.7851
-What is the probability that there will be more than 5 customers arriving within 1 hour?
A)0.1954
B)0.6288
C)0.2149
D)0.1563
E)0.7851

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
7
A street noodle vendor in Singapore can service an average of 10 customers per hour. Given an average arrival rate of 8 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-What is the probability of having exactly 4 customers arriving within 1 hour?
A)0.0107
B)0.0286
C)0.0573
D)0.0916
E)0.1221
-What is the probability of having exactly 4 customers arriving within 1 hour?
A)0.0107
B)0.0286
C)0.0573
D)0.0916
E)0.1221

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
8
A street noodle vendor in Singapore can service an average of 10 customers per hour. Given an average arrival rate of 8 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-What is the probability of having exactly 10 customers arriving within 1 hour?
A)0.8159
B)0.1221
C)0.1396
D)0.1241
E)0.0993
-What is the probability of having exactly 10 customers arriving within 1 hour?
A)0.8159
B)0.1221
C)0.1396
D)0.1241
E)0.0993

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
9
A street noodle vendor in Singapore can service an average of 10 customers per hour. Given an average arrival rate of 8 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-What is the probability of having, at most, 10 customers arriving within 1 hour?
A)0.8159
B)0.2834
C)0.1841
D)0.7166
E)0.0993
-What is the probability of having, at most, 10 customers arriving within 1 hour?
A)0.8159
B)0.2834
C)0.1841
D)0.7166
E)0.0993

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
10
A street noodle vendor in Singapore can service an average of 10 customers per hour. Given an average arrival rate of 8 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-What is the probability of having at least 10 customers arriving within 1 hour?
A)0.8159
B)0.2834
C)0.1841
D)0.7166
E)0.0993
-What is the probability of having at least 10 customers arriving within 1 hour?
A)0.8159
B)0.2834
C)0.1841
D)0.7166
E)0.0993

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
11
A street noodle vendor in Singapore can service an average of 10 customers per hour. Given an average arrival rate of 8 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-What is the probability of having more than 10 customers arriving within 1 hour?
A)0.8159
B)0.2834
C)0.1841
D)0.7166
E)0.0993
-What is the probability of having more than 10 customers arriving within 1 hour?
A)0.8159
B)0.2834
C)0.1841
D)0.7166
E)0.0993

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
12
A street noodle vendor in Singapore can service an average of 10 customers per hour. Given an average arrival rate of 8 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-What is the probability of having none of the customers arriving within 1 hour?
A)0.8159
B)0.0993
C)0.1841
D)0.0003
E)0.9997
-What is the probability of having none of the customers arriving within 1 hour?
A)0.8159
B)0.0993
C)0.1841
D)0.0003
E)0.9997

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
13
A street noodle vendor in Singapore can service an average of 10 customers per hour. Given an average arrival rate of 8 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-What is the probability of having exactly 12 customers arriving within 1 hour?
A)0.0481
B)0.9362
C)0.0638
D)0.8881
E)0.1119
-What is the probability of having exactly 12 customers arriving within 1 hour?
A)0.0481
B)0.9362
C)0.0638
D)0.8881
E)0.1119

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
14
A street noodle vendor in Singapore can service an average of 10 customers per hour. Given an average arrival rate of 8 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-What is the probability of having more than 12 customers arriving within 1 hour?
A)0.0481
B)0.9362
C)0.0638
D)0.8881
E)0.1119
-What is the probability of having more than 12 customers arriving within 1 hour?
A)0.0481
B)0.9362
C)0.0638
D)0.8881
E)0.1119

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
15
A street noodle vendor in Singapore can service an average of 10 customers per hour. Given an average arrival rate of 8 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-What is the probability of having exactly 15 customers arriving within 1 hour?
A)0.0003
B)0.0169
C)0.0082
D)0.9918
E)0.0090
-What is the probability of having exactly 15 customers arriving within 1 hour?
A)0.0003
B)0.0169
C)0.0082
D)0.9918
E)0.0090

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
16
A street noodle vendor in Singapore can service an average of 10 customers per hour. Given an average arrival rate of 8 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-What is the probability that exactly 10 customers will arrive in 1 hour, when the mean arrival rate is 15 customers per hour, and interarrival times are exponentially distributed?
A)0.0486
B)0.1185
C)0.0699
D)0.9301
E)0.8815
-What is the probability that exactly 10 customers will arrive in 1 hour, when the mean arrival rate is 15 customers per hour, and interarrival times are exponentially distributed?
A)0.0486
B)0.1185
C)0.0699
D)0.9301
E)0.8815

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
17
A street noodle vendor in Singapore can service an average of 10 customers per hour. Given an average arrival rate of 8 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-What is the probability that more than 10 customers will arrive in 1 hour, when the mean arrival rate is 15 customers per hour, and interarrival times are exponentially distributed?
A)0.0486
B)0.1185
C)0.0699
D)0.9301
E)0.8815
-What is the probability that more than 10 customers will arrive in 1 hour, when the mean arrival rate is 15 customers per hour, and interarrival times are exponentially distributed?
A)0.0486
B)0.1185
C)0.0699
D)0.9301
E)0.8815

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
18
A street noodle vendor in Singapore can service an average of 10 customers per hour. Given an average arrival rate of 8 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-What is the probability that less than 10 customers will arrive in 1 hour, when the mean arrival rate is 15 customers per hour and interarrival times are exponentially distributed?
A)0.0486
B)0.1185
C)0.0699
D)0.9301
E)0.8815
-What is the probability that less than 10 customers will arrive in 1 hour, when the mean arrival rate is 15 customers per hour and interarrival times are exponentially distributed?
A)0.0486
B)0.1185
C)0.0699
D)0.9301
E)0.8815

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
19
A street noodle vendor in Singapore can service an average of 10 customers per hour. Given an average arrival rate of 8 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-What is the probability that at least 10 customers will arrive in 1 hour, when the mean arrival rate is 15 customers per hour, and interarrival times are exponentially distributed?
A)0.0486
B)0.1185
C)0.0699
D)0.9301
E)0.8815
-What is the probability that at least 10 customers will arrive in 1 hour, when the mean arrival rate is 15 customers per hour, and interarrival times are exponentially distributed?
A)0.0486
B)0.1185
C)0.0699
D)0.9301
E)0.8815

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
20
A street noodle vendor in Singapore can service an average of 10 customers per hour. Given an average arrival rate of 8 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-What is the probability that, at most, 10 customers will arrive in 1 hour, when the mean arrival rate is 15 customers per hour, and interarrival times are exponentially distributed?
A)0.0486
B)0.1185
C)0.0699
D)0.9301
E)0.8815
-What is the probability that, at most, 10 customers will arrive in 1 hour, when the mean arrival rate is 15 customers per hour, and interarrival times are exponentially distributed?
A)0.0486
B)0.1185
C)0.0699
D)0.9301
E)0.8815

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
21
A street noodle vendor in Singapore can service an average of 10 customers per hour. Given an average arrival rate of 8 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-What is the probability that exactly 4 customers will arrive in 1 hour, when the mean arrival rate is 3 customers per hour, and interarrival times are exponentially distributed?
A)0.3528
B)0.1847
C)0.1680
D)0.8153
E)0.6472
-What is the probability that exactly 4 customers will arrive in 1 hour, when the mean arrival rate is 3 customers per hour, and interarrival times are exponentially distributed?
A)0.3528
B)0.1847
C)0.1680
D)0.8153
E)0.6472

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
22
A street noodle vendor in Singapore can service an average of 10 customers per hour. Given an average arrival rate of 8 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-What is the probability that more than 4 customers will arrive in 1 hour, when the mean arrival rate is 3 customers per hour, and interarrival times are exponentially distributed?
A)0.3528
B)0.1847
C)0.1680
D)0.8153
E)0.6472
-What is the probability that more than 4 customers will arrive in 1 hour, when the mean arrival rate is 3 customers per hour, and interarrival times are exponentially distributed?
A)0.3528
B)0.1847
C)0.1680
D)0.8153
E)0.6472

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
23
A street noodle vendor in Singapore can service an average of 10 customers per hour. Given an average arrival rate of 8 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-What is the probability that less than 4 customers will arrive in 1 hour, when the mean arrival rate is 3 customers per hour, and interarrival times are exponentially distributed?
A)0.3528
B)0.1847
C)0.1680
D)0.8153
E)0.6472
-What is the probability that less than 4 customers will arrive in 1 hour, when the mean arrival rate is 3 customers per hour, and interarrival times are exponentially distributed?
A)0.3528
B)0.1847
C)0.1680
D)0.8153
E)0.6472

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
24
A street noodle vendor in Singapore can service an average of 10 customers per hour. Given an average arrival rate of 8 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-What is the probability that at least 4 customers will arrive in 1 hour, when the mean arrival rate is 3 customers per hour, and interarrival times are exponentially distributed?
A)0.3528
B)0.1847
C)0.1680
D)0.8153
E)0.6472
-What is the probability that at least 4 customers will arrive in 1 hour, when the mean arrival rate is 3 customers per hour, and interarrival times are exponentially distributed?
A)0.3528
B)0.1847
C)0.1680
D)0.8153
E)0.6472

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
25
A street noodle vendor in Singapore can service an average of 10 customers per hour. Given an average arrival rate of 8 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-What is the probability that, at most, 4 customers will arrive in 1 hour, when the mean arrival rate is 3 customers per hour, and interarrival times are exponentially distributed?
A)0.3528
B)0.1847
C)0.1680
D)0.8153
E)0.6472
-What is the probability that, at most, 4 customers will arrive in 1 hour, when the mean arrival rate is 3 customers per hour, and interarrival times are exponentially distributed?
A)0.3528
B)0.1847
C)0.1680
D)0.8153
E)0.6472

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
26
A street noodle vendor in Singapore can service an average of 10 customers per hour. Given an average arrival rate of 8 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-What is the probability that no customer will arrive in 1 hour, when the mean arrival rate is 3 customers per hour, and interarrival times are exponentially distributed?
A)0.1680
B)0.2240
C)0.1494
D)0.9502
E)0.0498
-What is the probability that no customer will arrive in 1 hour, when the mean arrival rate is 3 customers per hour, and interarrival times are exponentially distributed?
A)0.1680
B)0.2240
C)0.1494
D)0.9502
E)0.0498

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
27
A street noodle vendor in Singapore can service an average of 10 customers per hour. Given an average arrival rate of 8 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-What is the probability that exactly 10 customers will arrive in 1 hour, when the mean arrival rate is 3 customers per hour, and interarrival times are exponentially distributed?
A)0.0027
B)0.0008
C)0.0002
D)0.9998
E)0.0498
-What is the probability that exactly 10 customers will arrive in 1 hour, when the mean arrival rate is 3 customers per hour, and interarrival times are exponentially distributed?
A)0.0027
B)0.0008
C)0.0002
D)0.9998
E)0.0498

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
28
A street noodle vendor in Singapore can service an average of 10 customers per hour. Given an average arrival rate of 8 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-What is the probability that more than 4 customers will arrive in 1 hour, when the mean arrival rate is 4 customers per hour, and interarrival times are exponentially distributed?
A)0.6288
B)0.1954
C)0.4335
D)0.5665
E)0.3712
-What is the probability that more than 4 customers will arrive in 1 hour, when the mean arrival rate is 4 customers per hour, and interarrival times are exponentially distributed?
A)0.6288
B)0.1954
C)0.4335
D)0.5665
E)0.3712

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
29
A street noodle vendor in Singapore can service an average of 10 customers per hour. Given an average arrival rate of 8 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-What is the probability that less than 2 customers will arrive in 1 hour, when the mean arrival rate is 2 customers per hour, and interarrival times are exponentially distributed?
A)0.4060
B)0.6767
C)0.3233
D)0.5940
E)0.2707
-What is the probability that less than 2 customers will arrive in 1 hour, when the mean arrival rate is 2 customers per hour, and interarrival times are exponentially distributed?
A)0.4060
B)0.6767
C)0.3233
D)0.5940
E)0.2707

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
30
A street noodle vendor in Singapore can service an average of 10 customers per hour. Given an average arrival rate of 8 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-What is the probability that exactly 30 calls arrive at a call center in an hour, when the mean arrival rate is 30 customer calls per hour, and interarrival times are exponentially distributed?
A)0.0511
B)0.0659
C)0.0702
D)0.0726
E)0.0453
-What is the probability that exactly 30 calls arrive at a call center in an hour, when the mean arrival rate is 30 customer calls per hour, and interarrival times are exponentially distributed?
A)0.0511
B)0.0659
C)0.0702
D)0.0726
E)0.0453

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
31
A street noodle vendor (one server) in Singapore can service an average of 20 customers per hour. Given an average arrival rate of 12 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-Calculate the mean server utilization.
A)20%
B)35%
C)50%
D)60%
E)75%
-Calculate the mean server utilization.
A)20%
B)35%
C)50%
D)60%
E)75%

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
32
A street noodle vendor (one server) in Singapore can service an average of 20 customers per hour. Given an average arrival rate of 12 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-Calculate the mean number of customers in the queue.
A)none
B)1.2
C)0.9
D)3.1
E)4.1
-Calculate the mean number of customers in the queue.
A)none
B)1.2
C)0.9
D)3.1
E)4.1

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
33
A street noodle vendor (one server) in Singapore can service an average of 20 customers per hour. Given an average arrival rate of 12 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-Calculate the mean number of customers in the system (being served and in the queue).
A)none
B)2.6
C)1.5
D)3.4
E)4.2
-Calculate the mean number of customers in the system (being served and in the queue).
A)none
B)2.6
C)1.5
D)3.4
E)4.2

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
34
A street noodle vendor (one server) in Singapore can service an average of 20 customers per hour. Given an average arrival rate of 12 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-Calculate the mean waiting time in the queue.
A)4.5 minutes
B)2.5 minutes
C)1.5 minutes
D)3.5 minutes
E)5 minutes
-Calculate the mean waiting time in the queue.
A)4.5 minutes
B)2.5 minutes
C)1.5 minutes
D)3.5 minutes
E)5 minutes

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
35
A street noodle vendor (one server) in Singapore can service an average of 20 customers per hour. Given an average arrival rate of 12 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-Calculate the mean waiting time in the system (being served and in the queue).
A)4.5 minutes
B)2.5 minutes
C)1.5 minutes
D)3.5 minutes
E)7.5 minutes
-Calculate the mean waiting time in the system (being served and in the queue).
A)4.5 minutes
B)2.5 minutes
C)1.5 minutes
D)3.5 minutes
E)7.5 minutes

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
36
A street noodle vendor (one server) in Singapore can service an average of 20 customers per hour. Given an average arrival rate of 12 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-What is the probability that there is no customer in the system at any given time?
A)20%
B)40%
C)24%
D)60%
E)36%
-What is the probability that there is no customer in the system at any given time?
A)20%
B)40%
C)24%
D)60%
E)36%

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
37
A street noodle vendor (one server) in Singapore can service an average of 20 customers per hour. Given an average arrival rate of 12 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-What is the probability that there is 1 customer in the system at any given time?
A)20%
B)40%
C)24%
D)60%
E)36%
-What is the probability that there is 1 customer in the system at any given time?
A)20%
B)40%
C)24%
D)60%
E)36%

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
38
A street noodle vendor (one server) in Singapore can service an average of 20 customers per hour. Given an average arrival rate of 12 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-What is the probability that there is more than 1 customer in the system at any given time?
A)20%
B)40%
C)24%
D)60%
E)36%
-What is the probability that there is more than 1 customer in the system at any given time?
A)20%
B)40%
C)24%
D)60%
E)36%

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
39
A street noodle vendor (one server) in Singapore can service an average of 20 customers per hour. Given an average arrival rate of 12 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-Change the arrival rate from 12 customers per hour to 10 customers per hour. What is the probability that there is more than 1 customer in the system at any given time?
A)25%
B)50%
C)75%
D)15%
E)36%
-Change the arrival rate from 12 customers per hour to 10 customers per hour. What is the probability that there is more than 1 customer in the system at any given time?
A)25%
B)50%
C)75%
D)15%
E)36%

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
40
A street noodle vendor (one server) in Singapore can service an average of 20 customers per hour. Given an average arrival rate of 12 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-Change the arrival rate of from 12 customers per hour to 15 customers per hour. What is the probability that there is more than 1 customer in the system at any given time?
A)25.00%
B)18.75%
C)43.75%
D)56.25%
E)36.00%
-Change the arrival rate of from 12 customers per hour to 15 customers per hour. What is the probability that there is more than 1 customer in the system at any given time?
A)25.00%
B)18.75%
C)43.75%
D)56.25%
E)36.00%

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
41
A street noodle vendor (one server) in Singapore can service an average of 20 customers per hour. Given an average arrival rate of 12 customers per hour, use the Poisson distribution to calculate the probability that the vendor can handle the demand.
-Change the number of customers the street vendor can serve per hour from 20 to 15. What is the probability that there is more than 1 customer in the system at any given time?
A)50%
B)36%
C)64%
D)20%
E)16%
-Change the number of customers the street vendor can serve per hour from 20 to 15. What is the probability that there is more than 1 customer in the system at any given time?
A)50%
B)36%
C)64%
D)20%
E)16%

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
42
Use the following information to determine the optimal overbooking policy for a spa center at downtown Marquette. The center's capacity is 12 guests. The historic number of no-shows for a typical day, along with the probability of occurrence, is shown in the following table. The average profitability per guest is $80, and the cost of lost goodwill per guest due to overbooking is approximately $40.

-Calculate the total expected profit with 12 reservations (and no overbooking).
A)$884
B)$922
C)$918
D)$960
E)Need additional information to calculate the total expected profit

-Calculate the total expected profit with 12 reservations (and no overbooking).
A)$884
B)$922
C)$918
D)$960
E)Need additional information to calculate the total expected profit

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
43
Use the following information to determine the optimal overbooking policy for a spa center at downtown Marquette. The center's capacity is 12 guests. The historic number of no-shows for a typical day, along with the probability of occurrence, is shown in the following table. The average profitability per guest is $80, and the cost of lost goodwill per guest due to overbooking is approximately $40.

-Calculate the total expected profit with 13 reservations (which means 1 overbooking).
A)$884
B)$922
C)$918
D)$960
E)Need additional information to calculate the total expected profit

-Calculate the total expected profit with 13 reservations (which means 1 overbooking).
A)$884
B)$922
C)$918
D)$960
E)Need additional information to calculate the total expected profit

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
44
Use the following information to determine the optimal overbooking policy for a spa center at downtown Marquette. The center's capacity is 12 guests. The historic number of no-shows for a typical day, along with the probability of occurrence, is shown in the following table. The average profitability per guest is $80, and the cost of lost goodwill per guest due to overbooking is approximately $40.

-Calculate the total expected profit with 14 reservations (which means 2 overbookings).
A)$884
B)$922
C)$918
D)$960
E)Need additional information to calculate the total expected profit

-Calculate the total expected profit with 14 reservations (which means 2 overbookings).
A)$884
B)$922
C)$918
D)$960
E)Need additional information to calculate the total expected profit

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
45
Use the following information to determine the optimal overbooking policy for a spa center at downtown Marquette. The center's capacity is 12 guests. The historic number of no-shows for a typical day, along with the probability of occurrence, is shown in the following table. The average profitability per guest is $80, and the cost of lost goodwill per guest due to overbooking is approximately $40.

-Based on the total expected profits obtained in Questions 41 through 43, which policy should be selected?
A)More than 14 reservations
B)12 reservations (that implies no overbooking)
C)14 reservations (that implies 2 overbookings)
D)13 reservations (that implies 1 overbooking)
E)Need additional information to calculate the total expected profit

-Based on the total expected profits obtained in Questions 41 through 43, which policy should be selected?
A)More than 14 reservations
B)12 reservations (that implies no overbooking)
C)14 reservations (that implies 2 overbookings)
D)13 reservations (that implies 1 overbooking)
E)Need additional information to calculate the total expected profit

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
46
Use the following information to determine the optimal overbooking policy for a motel at a rural town in South Carolina. The motel's capacity is 30 rooms. The historic number of no-shows for a typical day, along with the probability of occurrence, is shown in the following table. The average profitability per room is $110, and the cost of lost goodwill per guest due to overbooking is approximately $60.
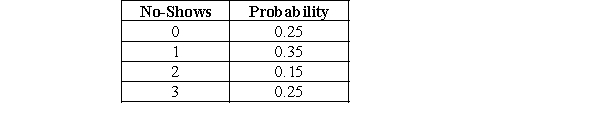
-Calculate the total expected profit with 30 reservations (and no overbooking).
A)$3,300.00
B)$2,886.00
C)$2,897.50
D)$2,883.50
E)$3,146.00

-Calculate the total expected profit with 30 reservations (and no overbooking).
A)$3,300.00
B)$2,886.00
C)$2,897.50
D)$2,883.50
E)$3,146.00

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
47
Use the following information to determine the optimal overbooking policy for a motel at a rural town in South Carolina. The motel's capacity is 30 rooms. The historic number of no-shows for a typical day, along with the probability of occurrence, is shown in the following table. The average profitability per room is $110, and the cost of lost goodwill per guest due to overbooking is approximately $60.

-Calculate the total expected profit with 31 reservations (which means 1 overbooking).
A)$3,300.00
B)$2,886.00
C)$2,897.50
D)$3,213.50
E)$2,827.00

-Calculate the total expected profit with 31 reservations (which means 1 overbooking).
A)$3,300.00
B)$2,886.00
C)$2,897.50
D)$3,213.50
E)$2,827.00

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
48
Use the following information to determine the optimal overbooking policy for a motel at a rural town in South Carolina. The motel's capacity is 30 rooms. The historic number of no-shows for a typical day, along with the probability of occurrence, is shown in the following table. The average profitability per room is $110, and the cost of lost goodwill per guest due to overbooking is approximately $60.

-Calculate the total expected profit with 32 reservations (which means 2 overbookings).
A)$3,300.00
B)$2,886.00
C)$2,897.50
D)$3,221.50
E)$2,827.00

-Calculate the total expected profit with 32 reservations (which means 2 overbookings).
A)$3,300.00
B)$2,886.00
C)$2,897.50
D)$3,221.50
E)$2,827.00

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
49
Use the following information to determine the optimal overbooking policy for a motel at a rural town in South Carolina. The motel's capacity is 30 rooms. The historic number of no-shows for a typical day, along with the probability of occurrence, is shown in the following table. The average profitability per room is $110, and the cost of lost goodwill per guest due to overbooking is approximately $60.

-Calculate the total expected profit with 33 reservations (which means 3 overbookings).
A)$3,300.00
B)$3,204.00
C)$2,897.50
D)$2,883.50
E)$2,827.00

-Calculate the total expected profit with 33 reservations (which means 3 overbookings).
A)$3,300.00
B)$3,204.00
C)$2,897.50
D)$2,883.50
E)$2,827.00

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
50
Use the following information to determine the optimal overbooking policy for a motel at a rural town in South Carolina. The motel's capacity is 30 rooms. The historic number of no-shows for a typical day, along with the probability of occurrence, is shown in the following table. The average profitability per room is $110, and the cost of lost goodwill per guest due to overbooking is approximately $60.

-Based on the total expected profits obtained in Questions 46 through 49, which policy should be selected?
A)More than 33 reservations
B)30 reservations (that implies no overbooking)
C)33 reservations (that implies 3 overbookings)
D)31 reservations (that implies 1 overbooking)
E)32 reservations (that implies 2 overbookings)

-Based on the total expected profits obtained in Questions 46 through 49, which policy should be selected?
A)More than 33 reservations
B)30 reservations (that implies no overbooking)
C)33 reservations (that implies 3 overbookings)
D)31 reservations (that implies 1 overbooking)
E)32 reservations (that implies 2 overbookings)

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck


