Deck 9: Comparing More Than Two Proportions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/46
Play
Full screen (f)
Deck 9: Comparing More Than Two Proportions
1
Researchers analyzed eating behavior and obesity at Chinese buffets. They estimated people's body mass indexes (BMI) as they entered the restaurant then categorized them into three groups---bottom third (lightest), middle third, and top third (heaviest). One variable they looked at was whether or not they browsed the buffet (looked it over) before serving themselves or served themselves immediately. Treating the BMI categories as the explanatory variable and whether or not they browsed first as the response, the researchers wanted to see if there was an association between BMI and whether or not they browsed the buffet before serving themselves. They found the following results:
• Bottom Third: 35 of the 50 people browsed first
• Middle Third: 24 of the 50 people browsed first
• Top Third: 17 of the 50 people browsed first
-Fill in the following two-way table with the observed data.

• Bottom Third: 35 of the 50 people browsed first
• Middle Third: 24 of the 50 people browsed first
• Top Third: 17 of the 50 people browsed first
-Fill in the following two-way table with the observed data.

Tol for each value = +/- 0 

2
Researchers analyzed eating behavior and obesity at Chinese buffets. They estimated people's body mass indexes (BMI) as they entered the restaurant then categorized them into three groups---bottom third (lightest), middle third, and top third (heaviest). One variable they looked at was whether or not they browsed the buffet (looked it over) before serving themselves or served themselves immediately. Treating the BMI categories as the explanatory variable and whether or not they browsed first as the response, the researchers wanted to see if there was an association between BMI and whether or not they browsed the buffet before serving themselves. They found the following results:
• Bottom Third: 35 of the 50 people browsed first
• Middle Third: 24 of the 50 people browsed first
• Top Third: 17 of the 50 people browsed first
-For each BMI category, calculate the conditional proportion of people that browsed first and write these numbers below as decimals, not fractions.
Bottom Third___________ Middle Third____________ Top Third____________
• Bottom Third: 35 of the 50 people browsed first
• Middle Third: 24 of the 50 people browsed first
• Top Third: 17 of the 50 people browsed first
-For each BMI category, calculate the conditional proportion of people that browsed first and write these numbers below as decimals, not fractions.
Bottom Third___________ Middle Third____________ Top Third____________
Bottom Third = 35/50 = 0.7; Middle Third = 0.48, Top Third = 0.34
3
Researchers analyzed eating behavior and obesity at Chinese buffets. They estimated people's body mass indexes (BMI) as they entered the restaurant then categorized them into three groups---bottom third (lightest), middle third, and top third (heaviest). One variable they looked at was whether or not they browsed the buffet (looked it over) before serving themselves or served themselves immediately. Treating the BMI categories as the explanatory variable and whether or not they browsed first as the response, the researchers wanted to see if there was an association between BMI and whether or not they browsed the buffet before serving themselves. They found the following results:
• Bottom Third: 35 of the 50 people browsed first
• Middle Third: 24 of the 50 people browsed first
• Top Third: 17 of the 50 people browsed first
-What is the null hypothesis to determine if there is an association between BMI and if a person browses first?
A) H _0:?1=?2=?3=0
B) H_0:x ?1=x ?2=x ?3=0
C) H_0:?1=?2=?3=0
D) H_0:p ?1=p ?2=p ?3=0
• Bottom Third: 35 of the 50 people browsed first
• Middle Third: 24 of the 50 people browsed first
• Top Third: 17 of the 50 people browsed first
-What is the null hypothesis to determine if there is an association between BMI and if a person browses first?
A) H _0:?1=?2=?3=0
B) H_0:x ?1=x ?2=x ?3=0
C) H_0:?1=?2=?3=0
D) H_0:p ?1=p ?2=p ?3=0
H_0:?1=?2=?3=0
4
Researchers analyzed eating behavior and obesity at Chinese buffets. They estimated people's body mass indexes (BMI) as they entered the restaurant then categorized them into three groups---bottom third (lightest), middle third, and top third (heaviest). One variable they looked at was whether or not they browsed the buffet (looked it over) before serving themselves or served themselves immediately. Treating the BMI categories as the explanatory variable and whether or not they browsed first as the response, the researchers wanted to see if there was an association between BMI and whether or not they browsed the buffet before serving themselves. They found the following results:
• Bottom Third: 35 of the 50 people browsed first
• Middle Third: 24 of the 50 people browsed first
• Top Third: 17 of the 50 people browsed first
-Compute the Mean Group Diff statistic.
• Bottom Third: 35 of the 50 people browsed first
• Middle Third: 24 of the 50 people browsed first
• Top Third: 17 of the 50 people browsed first
-Compute the Mean Group Diff statistic.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
5
Researchers analyzed eating behavior and obesity at Chinese buffets. They estimated people's body mass indexes (BMI) as they entered the restaurant then categorized them into three groups---bottom third (lightest), middle third, and top third (heaviest). One variable they looked at was whether or not they browsed the buffet (looked it over) before serving themselves or served themselves immediately. Treating the BMI categories as the explanatory variable and whether or not they browsed first as the response, the researchers wanted to see if there was an association between BMI and whether or not they browsed the buffet before serving themselves. They found the following results:
• Bottom Third: 35 of the 50 people browsed first
• Middle Third: 24 of the 50 people browsed first
• Top Third: 17 of the 50 people browsed first
-Use the Multiple Proportions applet to calculate an approximate p-value for this test. Use at least 1,000 shuffles.
• Bottom Third: 35 of the 50 people browsed first
• Middle Third: 24 of the 50 people browsed first
• Top Third: 17 of the 50 people browsed first
-Use the Multiple Proportions applet to calculate an approximate p-value for this test. Use at least 1,000 shuffles.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
6
Researchers analyzed eating behavior and obesity at Chinese buffets. They estimated people's body mass indexes (BMI) as they entered the restaurant then categorized them into three groups---bottom third (lightest), middle third, and top third (heaviest). One variable they looked at was whether or not they browsed the buffet (looked it over) before serving themselves or served themselves immediately. Treating the BMI categories as the explanatory variable and whether or not they browsed first as the response, the researchers wanted to see if there was an association between BMI and whether or not they browsed the buffet before serving themselves. They found the following results:
• Bottom Third: 35 of the 50 people browsed first
• Middle Third: 24 of the 50 people browsed first
• Top Third: 17 of the 50 people browsed first
-What is the shape of the resulting null distribution of MAD statistics shown in the output of the Multiple Proportions applet?
A) Symmetric
B) Normal
C) Left skewed
D) Right skewed
• Bottom Third: 35 of the 50 people browsed first
• Middle Third: 24 of the 50 people browsed first
• Top Third: 17 of the 50 people browsed first
-What is the shape of the resulting null distribution of MAD statistics shown in the output of the Multiple Proportions applet?
A) Symmetric
B) Normal
C) Left skewed
D) Right skewed

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
7
Researchers analyzed eating behavior and obesity at Chinese buffets. They estimated people's body mass indexes (BMI) as they entered the restaurant then categorized them into three groups---bottom third (lightest), middle third, and top third (heaviest). One variable they looked at was whether or not they browsed the buffet (looked it over) before serving themselves or served themselves immediately. Treating the BMI categories as the explanatory variable and whether or not they browsed first as the response, the researchers wanted to see if there was an association between BMI and whether or not they browsed the buffet before serving themselves. They found the following results:
• Bottom Third: 35 of the 50 people browsed first
• Middle Third: 24 of the 50 people browsed first
• Top Third: 17 of the 50 people browsed first
-Based upon the p-value of 0.001, what is the appropriate conclusion for this test?
A) We have strong evidence of an association between BMI and if a person browses first among all people who eat at Chinese buffets.
B) We have strong evidence of an association between BMI and if a person browses first among people who eat at Chinese buffets similar to those in the study.
C) We have strong evidence of no association between BMI and if a person browses first among all people who eat at Chinese buffets.
D) We have strong evidence of no association between BMI and if a person browses first among people who eat at Chinese buffets similar to those in the study.
• Bottom Third: 35 of the 50 people browsed first
• Middle Third: 24 of the 50 people browsed first
• Top Third: 17 of the 50 people browsed first
-Based upon the p-value of 0.001, what is the appropriate conclusion for this test?
A) We have strong evidence of an association between BMI and if a person browses first among all people who eat at Chinese buffets.
B) We have strong evidence of an association between BMI and if a person browses first among people who eat at Chinese buffets similar to those in the study.
C) We have strong evidence of no association between BMI and if a person browses first among all people who eat at Chinese buffets.
D) We have strong evidence of no association between BMI and if a person browses first among people who eat at Chinese buffets similar to those in the study.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
8
Which of the following is not one of the 3 "S"'s in the 3S strategy?
A) Simulate
B) Statistic
C) Sample
D) Strength of evidence
A) Simulate
B) Statistic
C) Sample
D) Strength of evidence

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
9
Suppose three students were interested in studying the association between a person's political party (Democrat, Republican, Independent, or Other), and whether they voted in the last election (Yes, No). Each of the three students selects a random sample of 40 students and asks each student their political party and if they voted in the last election. Their three Mean Group Diff statistics are:
Mean Group Diff 1 = 0.12 Mean Group Diff 2 = 0.35 Mean Group Diff 3 = 0.27
Which Mean Group Diff statistic provides the strongest evidence against the null hypothesis?
A) 0.12
B) 0.35
C) 0.27
Mean Group Diff 1 = 0.12 Mean Group Diff 2 = 0.35 Mean Group Diff 3 = 0.27
Which Mean Group Diff statistic provides the strongest evidence against the null hypothesis?
A) 0.12
B) 0.35
C) 0.27

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
10
As the Mean Group Diff statistic increases, the p-value decreases.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
11
The Mean Group Diff statistic can never be negative.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
12
The Mean Group Diff statistic is the average distance sample proportions are from each other.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
13
The Mean Group Diff statistic is the average of a group of sample proportions.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
14
Is there an association between a person's political affiliation (Democrat, Republican, or Inde-pendent) and whether or not they give to charity?
-Describe the appropriate parameter(s) and assign symbols(s) to the parameters. Select all that apply
A) ?Dem = probability that a Democrat will give to charity
B) ?Rep = probability that a Republican will give to charity
C) ?Ind = probability that a Independent will give to charity
-Describe the appropriate parameter(s) and assign symbols(s) to the parameters. Select all that apply
A) ?Dem = probability that a Democrat will give to charity
B) ?Rep = probability that a Republican will give to charity
C) ?Ind = probability that a Independent will give to charity

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
15
Is there an association between a person's political affiliation (Democrat, Republican, or Inde-pendent) and whether or not they give to charity?
-Assume that, in reality, there is no association between a person's political affiliation and whether or not they give to charity. Which of the following has the largest probability?
A) The p-value for a test of H 0:? Dem=? Rep is greater than 0.05.
B) The p-value for a test of H 0:? Dem=? Rep is greater than 0.05 AND the p-value for a test of H 0:? Dem=? Ind is greater than 0.05.
C) The p-value for a test of H 0:? Dem=? Rep is greater than 0.05 AND the p-value for a test of H 0:? Dem=? Ind is greater than 0.05 AND the p-value for a test of H 0:? Ind=? Rep is greater than 0.05.
D) All of the above have equal probability.
-Assume that, in reality, there is no association between a person's political affiliation and whether or not they give to charity. Which of the following has the largest probability?
A) The p-value for a test of H 0:? Dem=? Rep is greater than 0.05.
B) The p-value for a test of H 0:? Dem=? Rep is greater than 0.05 AND the p-value for a test of H 0:? Dem=? Ind is greater than 0.05.
C) The p-value for a test of H 0:? Dem=? Rep is greater than 0.05 AND the p-value for a test of H 0:? Dem=? Ind is greater than 0.05 AND the p-value for a test of H 0:? Ind=? Rep is greater than 0.05.
D) All of the above have equal probability.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
16
Hope student researchers want to determine if students yawning (when being yawned at) is asso-ciated with the time of day (morning, afternoon, and evening). They found the following results when they yawned in front of people around campus:
• Morning: 25 of the 39 people yawned
• Afternoon: 15 of the 38 people yawned
• Evening: 29 of the 44 people yawned
-Fill in the following two-way table with the observed data.

• Morning: 25 of the 39 people yawned
• Afternoon: 15 of the 38 people yawned
• Evening: 29 of the 44 people yawned
-Fill in the following two-way table with the observed data.


Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
17
Hope student researchers want to determine if students yawning (when being yawned at) is asso-ciated with the time of day (morning, afternoon, and evening). They found the following results when they yawned in front of people around campus:
• Morning: 25 of the 39 people yawned
• Afternoon: 15 of the 38 people yawned
• Evening: 29 of the 44 people yawned
-Are validity conditions met to conduct a chi-square test of association?
A) Yes, since 39, 38, and 44 are all larger than 20.
B) Yes, since 121 is larger than 20.
C) Yes, since each cell in the table has at least 10 observations.
D) No, since several cells in the table have less than 20 observations.
• Morning: 25 of the 39 people yawned
• Afternoon: 15 of the 38 people yawned
• Evening: 29 of the 44 people yawned
-Are validity conditions met to conduct a chi-square test of association?
A) Yes, since 39, 38, and 44 are all larger than 20.
B) Yes, since 121 is larger than 20.
C) Yes, since each cell in the table has at least 10 observations.
D) No, since several cells in the table have less than 20 observations.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
18
Hope student researchers want to determine if students yawning (when being yawned at) is asso-ciated with the time of day (morning, afternoon, and evening). They found the following results when they yawned in front of people around campus:
• Morning: 25 of the 39 people yawned
• Afternoon: 15 of the 38 people yawned
• Evening: 29 of the 44 people yawned
-For each time of day, calculate the conditional proportion of people that yawned and write these numbers as decimals not fractions.
Morning___________ Afternoon____________ Evening____________
• Morning: 25 of the 39 people yawned
• Afternoon: 15 of the 38 people yawned
• Evening: 29 of the 44 people yawned
-For each time of day, calculate the conditional proportion of people that yawned and write these numbers as decimals not fractions.
Morning___________ Afternoon____________ Evening____________

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
19
Hope student researchers want to determine if students yawning (when being yawned at) is asso-ciated with the time of day (morning, afternoon, and evening). They found the following results when they yawned in front of people around campus:
• Morning: 25 of the 39 people yawned
• Afternoon: 15 of the 38 people yawned
• Evening: 29 of the 44 people yawned
-Which applet would you use to conduct a theory-based test of association between time of day and whether a person yawns?
A) One Proportion
B) Two Proportions
C) Multiple Proportions
D) Theory-Based Inference
• Morning: 25 of the 39 people yawned
• Afternoon: 15 of the 38 people yawned
• Evening: 29 of the 44 people yawned
-Which applet would you use to conduct a theory-based test of association between time of day and whether a person yawns?
A) One Proportion
B) Two Proportions
C) Multiple Proportions
D) Theory-Based Inference

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
20
Hope student researchers want to determine if students yawning (when being yawned at) is asso-ciated with the time of day (morning, afternoon, and evening). They found the following results when they yawned in front of people around campus:
• Morning: 25 of the 39 people yawned
• Afternoon: 15 of the 38 people yawned
• Evening: 29 of the 44 people yawned
-When this test is run, a p-value of 0.03 is found. What would be an appropriate conclusion?
A) We have strong evidence that the probability a person yawns is different between all three times of day: morning, afternoon, and evening.
B) We have strong evidence of an association between time of day and whether a person yawns.
C) We have strong evidence of no association between time of day and whether a person yawns.
D) We do not have strong evidence of an association between time of day and whether a person yawns.
• Morning: 25 of the 39 people yawned
• Afternoon: 15 of the 38 people yawned
• Evening: 29 of the 44 people yawned
-When this test is run, a p-value of 0.03 is found. What would be an appropriate conclusion?
A) We have strong evidence that the probability a person yawns is different between all three times of day: morning, afternoon, and evening.
B) We have strong evidence of an association between time of day and whether a person yawns.
C) We have strong evidence of no association between time of day and whether a person yawns.
D) We do not have strong evidence of an association between time of day and whether a person yawns.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
21
Hope student researchers want to determine if students yawning (when being yawned at) is asso-ciated with the time of day (morning, afternoon, and evening). They found the following results when they yawned in front of people around campus:
• Morning: 25 of the 39 people yawned
• Afternoon: 15 of the 38 people yawned
• Evening: 29 of the 44 people yawned
-The chi-square statistic for this test was 6.991. If instead, the chi-square statistic had been 5.332, would the p-value be smaller, larger, or remain the same?
A) Smaller
B) Larger
C) Remain the same
• Morning: 25 of the 39 people yawned
• Afternoon: 15 of the 38 people yawned
• Evening: 29 of the 44 people yawned
-The chi-square statistic for this test was 6.991. If instead, the chi-square statistic had been 5.332, would the p-value be smaller, larger, or remain the same?
A) Smaller
B) Larger
C) Remain the same

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
22
Hope student researchers want to determine if students yawning (when being yawned at) is asso-ciated with the time of day (morning, afternoon, and evening). They found the following results when they yawned in front of people around campus:
• Morning: 25 of the 39 people yawned
• Afternoon: 15 of the 38 people yawned
• Evening: 29 of the 44 people yawned
-Follow-up confidence intervals for all pairwise differences in proportions are as follows:
•0.0299 to 0.4627: Morning - Afternoon
•-0.2237 to 0.1876: Morning - Evening
•-0.4736 to -0.0551: Afternoon - Evening
Based off of these intervals, which of the following conclusions are correct?
A) The probability of yawning in the morning differs significantly from the probability of yawning in the evening.
B) The probability of yawning in the morning differs significantly from the probability of yawning the afternoon.
C) The probability of yawning in the afternoon does not differ significantly from the probability of yawning in the evening.
D) The probability of yawning in the morning does not differ significantly from the probability of yawning in the afternoon.
• Morning: 25 of the 39 people yawned
• Afternoon: 15 of the 38 people yawned
• Evening: 29 of the 44 people yawned
-Follow-up confidence intervals for all pairwise differences in proportions are as follows:
•0.0299 to 0.4627: Morning - Afternoon
•-0.2237 to 0.1876: Morning - Evening
•-0.4736 to -0.0551: Afternoon - Evening
Based off of these intervals, which of the following conclusions are correct?
A) The probability of yawning in the morning differs significantly from the probability of yawning in the evening.
B) The probability of yawning in the morning differs significantly from the probability of yawning the afternoon.
C) The probability of yawning in the afternoon does not differ significantly from the probability of yawning in the evening.
D) The probability of yawning in the morning does not differ significantly from the probability of yawning in the afternoon.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
23
Can telling a joke affect whether or not a customer in a coffee bar leaves a tip for the waiter? A study investigated this question at a coffee bar in France. The waiter randomly assigned coffee-ordering customers into three groups: one received a card telling a joke with their bill, another group received a card containing an advertisement for a local restaurant, and the third received no card. The results are shown below. 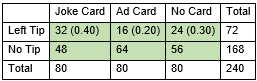
-Are validity conditions met to conduct a chi-square test of association?
A) Yes, since 80 is larger than 20.
B) Yes, since 240 is larger than 20.
C) Yes, since each cell in the table has at least 10 observations.
D) No, we did not collect a random sample of customers.

-Are validity conditions met to conduct a chi-square test of association?
A) Yes, since 80 is larger than 20.
B) Yes, since 240 is larger than 20.
C) Yes, since each cell in the table has at least 10 observations.
D) No, we did not collect a random sample of customers.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
24
Can telling a joke affect whether or not a customer in a coffee bar leaves a tip for the waiter? A study investigated this question at a coffee bar in France. The waiter randomly assigned coffee-ordering customers into three groups: one received a card telling a joke with their bill, another group received a card containing an advertisement for a local restaurant, and the third received no card. The results are shown below. 
-Use the Multiple Proportions applet to calculate the chi-square statistic and theory-based p-value for these data.
Chi-square statistic =
p-value =

-Use the Multiple Proportions applet to calculate the chi-square statistic and theory-based p-value for these data.
Chi-square statistic =
p-value =

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
25
Can telling a joke affect whether or not a customer in a coffee bar leaves a tip for the waiter? A study investigated this question at a coffee bar in France. The waiter randomly assigned coffee-ordering customers into three groups: one received a card telling a joke with their bill, another group received a card containing an advertisement for a local restaurant, and the third received no card. The results are shown below. 
-Use the Multiple Proportions applet to calculate the follow-up 95% confidence intervals for difference in proportions. Based on the output, which of the following statements are correct? Select all that apply.
A) The probability a customer leaves a tip is statistically significantly larger if a joke card is left than if an ad card is left.
B) The probability a customer leaves a tip is statistically significantly larger if a joke card is left than if no card is left.
C) The probability a customer leaves a tip is not statistically significantly different between the ad card and no card conditions.
D) The probability a customer leaves a tip is not statistically significantly different between the joke card and ad card conditions.

-Use the Multiple Proportions applet to calculate the follow-up 95% confidence intervals for difference in proportions. Based on the output, which of the following statements are correct? Select all that apply.
A) The probability a customer leaves a tip is statistically significantly larger if a joke card is left than if an ad card is left.
B) The probability a customer leaves a tip is statistically significantly larger if a joke card is left than if no card is left.
C) The probability a customer leaves a tip is not statistically significantly different between the ad card and no card conditions.
D) The probability a customer leaves a tip is not statistically significantly different between the joke card and ad card conditions.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
26
As the chi-square statistic increases, the p-value increases.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
27
As the chi-square statistic increases, we have more evidence against the null hypothesis.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
28
The chi-square statistic can be negative.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
29
The chi-square statistic is the ratio of variability between the groups and the variability within the groups.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
30
What shape is the distribution of the chi-square statistic?
A) Symmetric
B) Normal
C) Right skewed
D) Left skewed
A) Symmetric
B) Normal
C) Right skewed
D) Left skewed

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
31
Why do we do overall tests when comparing multiple proportions and not just do the follow-up confidence intervals?
A) Doing an overall test will more likely lead to significant results than just doing the follow-up confidence intervals.
B) Doing an overall test allows us to see exactly which group is significantly different from which other groups.
C) Doing an overall test allows us to quickly get our results, while the follow-up confidence intervals are very time-consuming.
D) Doing an overall test allows us to keep the probability of a type I error at 5% or whatever significance level we would like.
A) Doing an overall test will more likely lead to significant results than just doing the follow-up confidence intervals.
B) Doing an overall test allows us to see exactly which group is significantly different from which other groups.
C) Doing an overall test allows us to quickly get our results, while the follow-up confidence intervals are very time-consuming.
D) Doing an overall test allows us to keep the probability of a type I error at 5% or whatever significance level we would like.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
32
Suppose we conduct a chi-square goodness-of-fit test to determine if a 6-sided die is fair. We roll the die 10 times, and the resulting p-value is very large. What may we conclude? Select all that apply.
A) We have proven that the die is fair.
B) The hypothesis that the die is fair is plausible.
C) There is evidence that the die is fair.
D) There is evidence against the hypothesis that the die is not fair.
E) There is little to no evidence that the die is not fair. F. We have proven that the hypothesis that the die is not fair is false.
A) We have proven that the die is fair.
B) The hypothesis that the die is fair is plausible.
C) There is evidence that the die is fair.
D) There is evidence against the hypothesis that the die is not fair.
E) There is little to no evidence that the die is not fair. F. We have proven that the hypothesis that the die is not fair is false.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
33
Are people equally likely to be born on any day of the seven days of the week? Or are some days more likely to be a person's birthday than other days? To investigate this question, days of birth were recorded for the 147 "noted writers of the present" listed in The World Almanac and Book of Facts 2000. The counts for the seven days of the week are given in the following table. 
-Let ?_day be the probability that a person is born on a particular day. What is the null hypothesis?
A)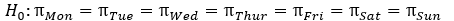
B)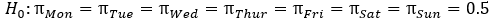
C)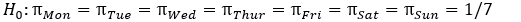
D)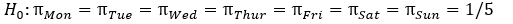

-Let ?_day be the probability that a person is born on a particular day. What is the null hypothesis?
A)
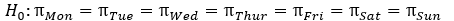
B)
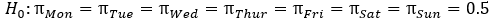
C)
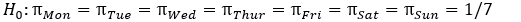
D)
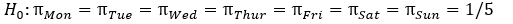

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
34
Are people equally likely to be born on any day of the seven days of the week? Or are some days more likely to be a person's birthday than other days? To investigate this question, days of birth were recorded for the 147 "noted writers of the present" listed in The World Almanac and Book of Facts 2000. The counts for the seven days of the week are given in the following table. 
-Fill in the table below with the expected counts based on the hypothesized model that people are equally likely to be born on any day of the seven days of the week.


-Fill in the table below with the expected counts based on the hypothesized model that people are equally likely to be born on any day of the seven days of the week.


Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
35
Are people equally likely to be born on any day of the seven days of the week? Or are some days more likely to be a person's birthday than other days? To investigate this question, days of birth were recorded for the 147 "noted writers of the present" listed in The World Almanac and Book of Facts 2000. The counts for the seven days of the week are given in the following table. 
-Use the Goodness of Fit applet to conduct a simulation-based chi-square goodness-of-fit test using the MAD (mean absolute difference) statistic, and report the statistic and the p-value. Use at least 1000 shuffles.
MAD statistic =
p-value =

-Use the Goodness of Fit applet to conduct a simulation-based chi-square goodness-of-fit test using the MAD (mean absolute difference) statistic, and report the statistic and the p-value. Use at least 1000 shuffles.
MAD statistic =
p-value =

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
36
Are people equally likely to be born on any day of the seven days of the week? Or are some days more likely to be a person's birthday than other days? To investigate this question, days of birth were recorded for the 147 "noted writers of the present" listed in The World Almanac and Book of Facts 2000. The counts for the seven days of the week are given in the following table. 
-Use the Goodness of Fit applet to conduct a simulation-based chi-square goodness-of-fit test using the chi-square statistic, and report the statistic and the p-value. Use at least 1000 shuffles.
chi-square statistic =
p-value =

-Use the Goodness of Fit applet to conduct a simulation-based chi-square goodness-of-fit test using the chi-square statistic, and report the statistic and the p-value. Use at least 1000 shuffles.
chi-square statistic =
p-value =

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
37
Are people equally likely to be born on any day of the seven days of the week? Or are some days more likely to be a person's birthday than other days? To investigate this question, days of birth were recorded for the 147 "noted writers of the present" listed in The World Almanac and Book of Facts 2000. The counts for the seven days of the week are given in the following table. 
-Use the Goodness of Fit applet to conduct a theory-based chi-square goodness-of-fit test, and report the chi-square statistic and the p-value.
chi-square statistic =
p-value =

-Use the Goodness of Fit applet to conduct a theory-based chi-square goodness-of-fit test, and report the chi-square statistic and the p-value.
chi-square statistic =
p-value =

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
38
Are people equally likely to be born on any day of the seven days of the week? Or are some days more likely to be a person's birthday than other days? To investigate this question, days of birth were recorded for the 147 "noted writers of the present" listed in The World Almanac and Book of Facts 2000. The counts for the seven days of the week are given in the following table. 
-Are validity conditions met to conduct a theory-based chi-square goodness-of-fit test?
A) Yes, since all observed counts are at least 10.
B) Yes, since we have at least 10 successes and 10 failures.
C) No, since the p-values in questions 35 and 37 were different.
D) No, since this was not a random sample.

-Are validity conditions met to conduct a theory-based chi-square goodness-of-fit test?
A) Yes, since all observed counts are at least 10.
B) Yes, since we have at least 10 successes and 10 failures.
C) No, since the p-values in questions 35 and 37 were different.
D) No, since this was not a random sample.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
39
Are people equally likely to be born on any day of the seven days of the week? Or are some days more likely to be a person's birthday than other days? To investigate this question, days of birth were recorded for the 147 "noted writers of the present" listed in The World Almanac and Book of Facts 2000. The counts for the seven days of the week are given in the following table. 
-Based upon a p-value of 0.53, what is the appropriate conclusion for the test?
A) We have strong evidence that people are equally likely to be born on any day of the seven days of the week.
B) We do not have strong evidence that people are equally likely to be born on any day of the seven days of the week.
C) We have strong evidence that people are not equally likely to be born on any day of the seven days of the week.
D) We do not have strong evidence that people are not equally likely to be born on any day of the seven days of the week.

-Based upon a p-value of 0.53, what is the appropriate conclusion for the test?
A) We have strong evidence that people are equally likely to be born on any day of the seven days of the week.
B) We do not have strong evidence that people are equally likely to be born on any day of the seven days of the week.
C) We have strong evidence that people are not equally likely to be born on any day of the seven days of the week.
D) We do not have strong evidence that people are not equally likely to be born on any day of the seven days of the week.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
40
According to the 2019 U.S. Census Bureau estimates, 63.4% of the U.S. self-identifies as Non-Hispanic white, 15.3% as Hispanic and Latino, 13.4% as Black or African American, 5.9% as Asian, and 2.0% as Other. A random sample of 1000 students graduating from California colleges and universities resulted in the following data on self-identified race:  You would like to determine if the distribution of self-identified race among California college and university students differs from the distribution of self-identified race in the U.S. overall.
You would like to determine if the distribution of self-identified race among California college and university students differs from the distribution of self-identified race in the U.S. overall.
-What is the null hypothesis? Fill in the value for each parameter.

 You would like to determine if the distribution of self-identified race among California college and university students differs from the distribution of self-identified race in the U.S. overall.
You would like to determine if the distribution of self-identified race among California college and university students differs from the distribution of self-identified race in the U.S. overall.-What is the null hypothesis? Fill in the value for each parameter.


Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
41
According to the 2019 U.S. Census Bureau estimates, 63.4% of the U.S. self-identifies as Non-Hispanic white, 15.3% as Hispanic and Latino, 13.4% as Black or African American, 5.9% as Asian, and 2.0% as Other. A random sample of 1000 students graduating from California colleges and universities resulted in the following data on self-identified race:  You would like to determine if the distribution of self-identified race among California college and university students differs from the distribution of self-identified race in the U.S. overall.
You would like to determine if the distribution of self-identified race among California college and university students differs from the distribution of self-identified race in the U.S. overall.
-In the null hypothesis, what does the symbol ?_Race represent?
A) The proportion of the U.S. that self-identify as a certain Race
B) The proportion of Californians that self-identify as a certain Race
C) The proportion of all students graduating from California colleges and universities that self-identify as a certain Race
D) The proportion of the sample of 1000 students that self-identified as a certain Race
 You would like to determine if the distribution of self-identified race among California college and university students differs from the distribution of self-identified race in the U.S. overall.
You would like to determine if the distribution of self-identified race among California college and university students differs from the distribution of self-identified race in the U.S. overall.-In the null hypothesis, what does the symbol ?_Race represent?
A) The proportion of the U.S. that self-identify as a certain Race
B) The proportion of Californians that self-identify as a certain Race
C) The proportion of all students graduating from California colleges and universities that self-identify as a certain Race
D) The proportion of the sample of 1000 students that self-identified as a certain Race

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
42
According to the 2019 U.S. Census Bureau estimates, 63.4% of the U.S. self-identifies as Non-Hispanic white, 15.3% as Hispanic and Latino, 13.4% as Black or African American, 5.9% as Asian, and 2.0% as Other. A random sample of 1000 students graduating from California colleges and universities resulted in the following data on self-identified race:  You would like to determine if the distribution of self-identified race among California college and university students differs from the distribution of self-identified race in the U.S. overall.
You would like to determine if the distribution of self-identified race among California college and university students differs from the distribution of self-identified race in the U.S. overall.
-What is the expected count based on the null model for the "Hispanic or Latino" cell?
A) 77
B) 15.3
C) 11.8
D) 153
 You would like to determine if the distribution of self-identified race among California college and university students differs from the distribution of self-identified race in the U.S. overall.
You would like to determine if the distribution of self-identified race among California college and university students differs from the distribution of self-identified race in the U.S. overall.-What is the expected count based on the null model for the "Hispanic or Latino" cell?
A) 77
B) 15.3
C) 11.8
D) 153

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
43
According to the 2019 U.S. Census Bureau estimates, 63.4% of the U.S. self-identifies as Non-Hispanic white, 15.3% as Hispanic and Latino, 13.4% as Black or African American, 5.9% as Asian, and 2.0% as Other. A random sample of 1000 students graduating from California colleges and universities resulted in the following data on self-identified race:  You would like to determine if the distribution of self-identified race among California college and university students differs from the distribution of self-identified race in the U.S. overall.
You would like to determine if the distribution of self-identified race among California college and university students differs from the distribution of self-identified race in the U.S. overall.
-Use the Goodness of Fit applet to conduct a simulation-based chi-square goodness-of-fit test using the chi-square statistic, and report the statistic and the p-value. Use at least 1000 shuffles.
chi-square statistic =
p-value =
 You would like to determine if the distribution of self-identified race among California college and university students differs from the distribution of self-identified race in the U.S. overall.
You would like to determine if the distribution of self-identified race among California college and university students differs from the distribution of self-identified race in the U.S. overall.-Use the Goodness of Fit applet to conduct a simulation-based chi-square goodness-of-fit test using the chi-square statistic, and report the statistic and the p-value. Use at least 1000 shuffles.
chi-square statistic =
p-value =

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
44
According to the 2019 U.S. Census Bureau estimates, 63.4% of the U.S. self-identifies as Non-Hispanic white, 15.3% as Hispanic and Latino, 13.4% as Black or African American, 5.9% as Asian, and 2.0% as Other. A random sample of 1000 students graduating from California colleges and universities resulted in the following data on self-identified race:  You would like to determine if the distribution of self-identified race among California college and university students differs from the distribution of self-identified race in the U.S. overall.
You would like to determine if the distribution of self-identified race among California college and university students differs from the distribution of self-identified race in the U.S. overall.
-Use the
Goodness of Fit applet to conduct a simulation-based chi-square goodness-of-fit test using the MAD (mean absolute difference) statistic, and report the statistic and the p-value. Use at least 1000 shuffles.
MAD statistic =
p-value =
 You would like to determine if the distribution of self-identified race among California college and university students differs from the distribution of self-identified race in the U.S. overall.
You would like to determine if the distribution of self-identified race among California college and university students differs from the distribution of self-identified race in the U.S. overall.-Use the
Goodness of Fit applet to conduct a simulation-based chi-square goodness-of-fit test using the MAD (mean absolute difference) statistic, and report the statistic and the p-value. Use at least 1000 shuffles.
MAD statistic =
p-value =

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
45
According to the 2019 U.S. Census Bureau estimates, 63.4% of the U.S. self-identifies as Non-Hispanic white, 15.3% as Hispanic and Latino, 13.4% as Black or African American, 5.9% as Asian, and 2.0% as Other. A random sample of 1000 students graduating from California colleges and universities resulted in the following data on self-identified race:  You would like to determine if the distribution of self-identified race among California college and university students differs from the distribution of self-identified race in the U.S. overall.
You would like to determine if the distribution of self-identified race among California college and university students differs from the distribution of self-identified race in the U.S. overall.
-Based upon a p-value of less than 0.001, what is an appropriate conclusion for the goodness-of-fit test?
A) We do not have strong evidence that the distribution of self-identified race among California college and university students differs from the distribution of self-identified race in the U.S. overall.
B) We have strong evidence that the distribution of self-identified race among California college and university students differs from the distribution of self-identified race in the U.S. overall.
C) We have strong evidence that the distribution of self-identified race among California college and university students is the same as the distribution of self-identified race in the U.S. overall.
D) We have strong evidence that the probabilities of each self-identified race among California college and university students are not all equal.
 You would like to determine if the distribution of self-identified race among California college and university students differs from the distribution of self-identified race in the U.S. overall.
You would like to determine if the distribution of self-identified race among California college and university students differs from the distribution of self-identified race in the U.S. overall.-Based upon a p-value of less than 0.001, what is an appropriate conclusion for the goodness-of-fit test?
A) We do not have strong evidence that the distribution of self-identified race among California college and university students differs from the distribution of self-identified race in the U.S. overall.
B) We have strong evidence that the distribution of self-identified race among California college and university students differs from the distribution of self-identified race in the U.S. overall.
C) We have strong evidence that the distribution of self-identified race among California college and university students is the same as the distribution of self-identified race in the U.S. overall.
D) We have strong evidence that the probabilities of each self-identified race among California college and university students are not all equal.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
46
According to the 2019 U.S. Census Bureau estimates, 63.4% of the U.S. self-identifies as Non-Hispanic white, 15.3% as Hispanic and Latino, 13.4% as Black or African American, 5.9% as Asian, and 2.0% as Other. A random sample of 1000 students graduating from California colleges and universities resulted in the following data on self-identified race:  You would like to determine if the distribution of self-identified race among California college and university students differs from the distribution of self-identified race in the U.S. overall.
You would like to determine if the distribution of self-identified race among California college and university students differs from the distribution of self-identified race in the U.S. overall.
-Are the validity conditions met for a theory-based chi-square goodness-of-fit test?
A) Yes, since 1000 is larger than 20.
B) Yes, since all of the expected counts are at least 10.
C) No, since the observed count for Other is less than 10.
D) Yes, since the p-values from both the simulation-based and theory-based tests are similar.
 You would like to determine if the distribution of self-identified race among California college and university students differs from the distribution of self-identified race in the U.S. overall.
You would like to determine if the distribution of self-identified race among California college and university students differs from the distribution of self-identified race in the U.S. overall.-Are the validity conditions met for a theory-based chi-square goodness-of-fit test?
A) Yes, since 1000 is larger than 20.
B) Yes, since all of the expected counts are at least 10.
C) No, since the observed count for Other is less than 10.
D) Yes, since the p-values from both the simulation-based and theory-based tests are similar.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck


