Deck 2: Significance: How Strong Is the Evidence
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/75
Play
Full screen (f)
Deck 2: Significance: How Strong Is the Evidence
1
Do red uniform wearers tend to win more often than those wearing blue uniforms in Taekwondo matches where competitors are randomly assigned to wear either a red or blue uniform? In a sample of 80 Taekwondo matches, there were 45 matches where the red uni-form wearer won.
-What is the parameter of interest for this study?
A) The long-run proportion of Taekwondo matches in which the red uniform wearer wins
B) The proportion of matches in which the red uniform wearer wins in a sample of 80 Taekwondo matches
C) Whether the red uniform wearer wins a match
D) 0.50
-What is the parameter of interest for this study?
A) The long-run proportion of Taekwondo matches in which the red uniform wearer wins
B) The proportion of matches in which the red uniform wearer wins in a sample of 80 Taekwondo matches
C) Whether the red uniform wearer wins a match
D) 0.50
The long-run proportion of Taekwondo matches in which the red uniform wearer wins
2
Do red uniform wearers tend to win more often than those wearing blue uniforms in Taekwondo matches where competitors are randomly assigned to wear either a red or blue uniform? In a sample of 80 Taekwondo matches, there were 45 matches where the red uni-form wearer won.
-What is the statistic for this study?
A) The long-run proportion of Taekwondo matches in which the red uniform wearer wins
B) The proportion of matches in which the red uniform wearer wins in a sample of 80 Taekwondo matches
C) Whether the red uniform wearer wins a match
D) 0.50
-What is the statistic for this study?
A) The long-run proportion of Taekwondo matches in which the red uniform wearer wins
B) The proportion of matches in which the red uniform wearer wins in a sample of 80 Taekwondo matches
C) Whether the red uniform wearer wins a match
D) 0.50
The proportion of matches in which the red uniform wearer wins in a sample of 80 Taekwondo matches
3
Do red uniform wearers tend to win more often than those wearing blue uniforms in Taekwondo matches where competitors are randomly assigned to wear either a red or blue uniform? In a sample of 80 Taekwondo matches, there were 45 matches where the red uni-form wearer won.
-Given below is the simulated distribution of the number of "red wins" that could happen by chance alone in a sample of 80 matches. Based on this simulation, is our observed result statistically significant?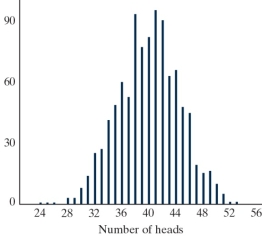
A) Yes, since 45 is larger than 40.
B) Yes, since the height of the dotplot above 45 is smaller than the height of the dotplot above 40.
C) No, since 45 is a fairly typical outcome if the color of the winner's uniform was determined by chance alone.
D) No, since we could have observed a value greater than 45 just by random chance.
-Given below is the simulated distribution of the number of "red wins" that could happen by chance alone in a sample of 80 matches. Based on this simulation, is our observed result statistically significant?

A) Yes, since 45 is larger than 40.
B) Yes, since the height of the dotplot above 45 is smaller than the height of the dotplot above 40.
C) No, since 45 is a fairly typical outcome if the color of the winner's uniform was determined by chance alone.
D) No, since we could have observed a value greater than 45 just by random chance.
No, since 45 is a fairly typical outcome if the color of the winner's uniform was determined by chance alone.
4
Do red uniform wearers tend to win more often than those wearing blue uniforms in Taekwondo matches where competitors are randomly assigned to wear either a red or blue uniform? In a sample of 80 Taekwondo matches, there were 45 matches where the red uni-form wearer won.
-What can we conclude from the results of this study? Select all that apply.
A) The results of this study are something that could easily have happened if the color of the winner's uniform was determined by chance alone.
B) We do not have convincing evidence against the "by-chance-alone" model.
C) The results of this study prove that the color of the winner's uniform was determined by chance alone.
D) We do not have convincing evidence that red uniform wearers tend to win more often than those wearing blue uniforms.
-What can we conclude from the results of this study? Select all that apply.
A) The results of this study are something that could easily have happened if the color of the winner's uniform was determined by chance alone.
B) We do not have convincing evidence against the "by-chance-alone" model.
C) The results of this study prove that the color of the winner's uniform was determined by chance alone.
D) We do not have convincing evidence that red uniform wearers tend to win more often than those wearing blue uniforms.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
5
Suppose you are testing to see if your dog, Hope, understands pointing towards an object. You place two objects about 2.5 meters away, then you point towards one of the objects. In 20 trials, Hope goes to the correct object 13 times (or 65%).
-Fill in the blanks with the correct One Proportion applet inputs to carry out an appropriate simulation of this process, if Hope does not understand pointing towards an object and is just guessing.
Probability of success: _______
Sample size: _______
Number of samples: _______
-Fill in the blanks with the correct One Proportion applet inputs to carry out an appropriate simulation of this process, if Hope does not understand pointing towards an object and is just guessing.
Probability of success: _______
Sample size: _______
Number of samples: _______

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
6
Match the parts of the real study corresponding to the physical (coin-flipping) simulation:
-Coin flip = _______
A) 0.5, probability of Hope going to the correct object
B) Hope going to the correct object
C) Hope going to the incorrect object
D) One set of 20 attempts by Hope
E) Hope going to an object
-Coin flip = _______
A) 0.5, probability of Hope going to the correct object
B) Hope going to the correct object
C) Hope going to the incorrect object
D) One set of 20 attempts by Hope
E) Hope going to an object

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
7
Match the parts of the real study corresponding to the physical (coin-flipping) simulation:
-Heads = _______
A) 0.5, probability of Hope going to the correct object
B) Hope going to the correct object
C) Hope going to the incorrect object
D) One set of 20 attempts by Hope
E) Hope going to an object
-Heads = _______
A) 0.5, probability of Hope going to the correct object
B) Hope going to the correct object
C) Hope going to the incorrect object
D) One set of 20 attempts by Hope
E) Hope going to an object

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
8
Match the parts of the real study corresponding to the physical (coin-flipping) simulation:
-Tails = _______
A) 0.5, probability of Hope going to the correct object
B) Hope going to the correct object
C) Hope going to the incorrect object
D) One set of 20 attempts by Hope
E) Hope going to an object
-Tails = _______
A) 0.5, probability of Hope going to the correct object
B) Hope going to the correct object
C) Hope going to the incorrect object
D) One set of 20 attempts by Hope
E) Hope going to an object

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
9
Match the parts of the real study corresponding to the physical (coin-flipping) simulation:
-Chance of heads = _______
A) 0.5, probability of Hope going to the correct object
B) Hope going to the correct object
C) Hope going to the incorrect object
D) One set of 20 attempts by Hope
E) Hope going to an object
-Chance of heads = _______
A) 0.5, probability of Hope going to the correct object
B) Hope going to the correct object
C) Hope going to the incorrect object
D) One set of 20 attempts by Hope
E) Hope going to an object

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
10
Match the parts of the real study corresponding to the physical (coin-flipping) simulation:
-One repetition = _______
A) 0.5, probability of Hope going to the correct object
B) Hope going to the correct object
C) Hope going to the incorrect object
D) One set of 20 attempts by Hope
E) Hope going to an object
-One repetition = _______
A) 0.5, probability of Hope going to the correct object
B) Hope going to the correct object
C) Hope going to the incorrect object
D) One set of 20 attempts by Hope
E) Hope going to an object

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
11
Suppose you are testing to see if your dog, Hope, understands pointing towards an object. You place two objects about 2.5 meters away, then you point towards one of the objects. In 20 trials, Hope goes to the correct object 13 times (or 65%).
-Given below is the resulting simulation distribution from the One Proportion applet. Based on this simulation, do we have convincing evidence against the observed study results happening by chance alone?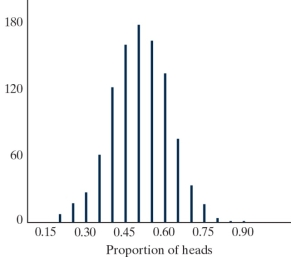
A) No, since 0.65 is a fairly typical outcome if Hope was just guessing.
B) No, since we could have observed a value greater than 0.65 just by random chance.
C) Yes, since 0.65 is larger than 0.5.
D) Yes, since the height of the dotplot above 0.65 is smaller than the height of the dotplot above 0.5.
-Given below is the resulting simulation distribution from the One Proportion applet. Based on this simulation, do we have convincing evidence against the observed study results happening by chance alone?

A) No, since 0.65 is a fairly typical outcome if Hope was just guessing.
B) No, since we could have observed a value greater than 0.65 just by random chance.
C) Yes, since 0.65 is larger than 0.5.
D) Yes, since the height of the dotplot above 0.65 is smaller than the height of the dotplot above 0.5.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
12
Suppose you are testing to see if your dog, Hope, understands pointing towards an object. You place two objects about 2.5 meters away, then you point towards one of the objects. In 20 trials, Hope goes to the correct object 13 times (or 65%).
-Which of the following is NOT a step in the 3S Strategy for measuring strength of evidence?
A) Strength of evidence
B) Statistic
C) Sample
D) Simulate
-Which of the following is NOT a step in the 3S Strategy for measuring strength of evidence?
A) Strength of evidence
B) Statistic
C) Sample
D) Simulate

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
13
A parameter is a number summarizing the results in the sample.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
14
A result that is unlikely to occur just by chance alone is called statistically significant.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
15
If an observed statistic is statistically significant, then we have strong evidence that the chance-alone explanation is correct.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
16
If an observed statistic is NOT statistically significant, then the chance model is plausible.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
17
A survey on 1,500 high school seniors who took the SAT and who completed an optional web survey shows that 55% of high school seniors are fairly certain that they will participate in a study abroad program in college. Does this survey provide convincing evidence that the majority (more than 50%) of all high school seniors who take the SAT are fairly certain they will participate in a study abroad program in college?
-What is the value of the statistic and its proper notation in this study?
A)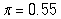
B)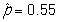
C)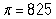
D)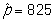
-What is the value of the statistic and its proper notation in this study?
A)
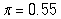
B)
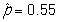
C)
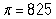
D)
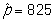

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
18
A survey on 1,500 high school seniors who took the SAT and who completed an optional web survey shows that 55% of high school seniors are fairly certain that they will participate in a study abroad program in college. Does this survey provide convincing evidence that the majority (more than 50%) of all high school seniors who take the SAT are fairly certain they will participate in a study abroad program in college?
-Under the null hypothesis, what is the value of the parameter of interest and its proper notation in this study?
A) ?=0.50
B) p ?=0.50
C)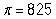
D)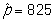
-Under the null hypothesis, what is the value of the parameter of interest and its proper notation in this study?
A) ?=0.50
B) p ?=0.50
C)
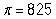
D)
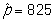

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
19
A survey on 1,500 high school seniors who took the SAT and who completed an optional web survey shows that 55% of high school seniors are fairly certain that they will participate in a study abroad program in college. Does this survey provide convincing evidence that the majority (more than 50%) of all high school seniors who take the SAT are fairly certain they will participate in a study abroad program in college?
-State the null and alternative hypotheses in proper notation.
A)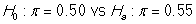
B)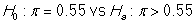
C)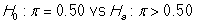
D)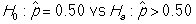
-State the null and alternative hypotheses in proper notation.
A)
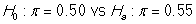
B)
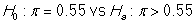
C)
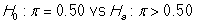
D)
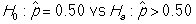

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
20
A survey on 1,500 high school seniors who took the SAT and who completed an optional web survey shows that 55% of high school seniors are fairly certain that they will participate in a study abroad program in college. Does this survey provide convincing evidence that the majority (more than 50%) of all high school seniors who take the SAT are fairly certain they will participate in a study abroad program in college?
-Fill in the blanks with the correct values to simulate another survey of 1,500 high school seniors who took the SAT in which the long-run proportion of all high school seniors who take the SAT that are fairly certain they will participate in a study abroad program in college is 0.50.
Create a spinner with ______ percent shaded red, and _____ percent shaded black. Spin the spinner _____ times. Record the _____ of times the spinner lands on red.
-Fill in the blanks with the correct values to simulate another survey of 1,500 high school seniors who took the SAT in which the long-run proportion of all high school seniors who take the SAT that are fairly certain they will participate in a study abroad program in college is 0.50.
Create a spinner with ______ percent shaded red, and _____ percent shaded black. Spin the spinner _____ times. Record the _____ of times the spinner lands on red.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
21
A survey on 1,500 high school seniors who took the SAT and who completed an optional web survey shows that 55% of high school seniors are fairly certain that they will participate in a study abroad program in college. Does this survey provide convincing evidence that the majority (more than 50%) of all high school seniors who take the SAT are fairly certain they will participate in a study abroad program in college?
-Using a count as the statistic, where would you expect the null distribution to be centered?
A) 0.55
B) 0.50
C) 825
D) 750
-Using a count as the statistic, where would you expect the null distribution to be centered?
A) 0.55
B) 0.50
C) 825
D) 750

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
22
A survey on 1,500 high school seniors who took the SAT and who completed an optional web survey shows that 55% of high school seniors are fairly certain that they will participate in a study abroad program in college. Does this survey provide convincing evidence that the majority (more than 50%) of all high school seniors who take the SAT are fairly certain they will participate in a study abroad program in college?
-The p-value for this study is less than 0.001. Interpret this value in the context of the problem.
A) There is less than a 0.1% chance that 50% of all high school seniors who take the SAT are fairly certain they will participate in a study abroad program in college.
B) In less than 0.1% of all samples of 1,500 high school seniors who take the SAT, we would see 55% or more respond that they are fairly certain they will participate in a study abroad program in college, if the true probability is 0.50.
C) In less than 0.1% of all samples of 1,500 high school seniors who take the SAT, we would see 50% or more respond that they are fairly certain they will participate in a study abroad program in college, if the true probability is 0.55.
D) There is less than a 0.1% chance that more than 50% of all high school seniors who take the SAT are fairly certain they will participate in a study abroad program in college.
-The p-value for this study is less than 0.001. Interpret this value in the context of the problem.
A) There is less than a 0.1% chance that 50% of all high school seniors who take the SAT are fairly certain they will participate in a study abroad program in college.
B) In less than 0.1% of all samples of 1,500 high school seniors who take the SAT, we would see 55% or more respond that they are fairly certain they will participate in a study abroad program in college, if the true probability is 0.50.
C) In less than 0.1% of all samples of 1,500 high school seniors who take the SAT, we would see 50% or more respond that they are fairly certain they will participate in a study abroad program in college, if the true probability is 0.55.
D) There is less than a 0.1% chance that more than 50% of all high school seniors who take the SAT are fairly certain they will participate in a study abroad program in college.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
23
Research done in the mid 1980s indicated that 80% of grizzly bears in the greater ecosystem of Yellowstone National Park entered their den for hibernation by the last day of November. This has come into question as of late. Researchers have hypothesized that climate change has postponed bears entering hibernation until later in the season; that is, researchers believe that a smaller percentage of bears are entering their den for hibernation by the last day of November. Sixty-two Yellowstone grizzly bears were tracked via radio monitors, which allow scientists to pinpoint when the bears enter their dens with a high degree of accuracy. Of the sixty-two Yellowstone grizzly bears being tracked, forty-two entered their den for hibernation by the last day of November.
-Identify which of the following is the null hypothesis, and which is the alternative hypothesis:
_____The sample proportion of 62 Yellowstone grizzly bears that enter their den for hibernation by the last day of November is 0.80.
_____The long-run proportion of Yellowstone grizzly bears that enter their den for hibernation by the last day of November is 0.80.
_____ The long-run proportion of Yellowstone grizzly bears that enter their den for hibernation by the last day of November is less than 0.80.
_____ The long-run proportion of Yellowstone grizzly bears that enter their den for hibernation by the last day of November is greater than 0.80.
-Identify which of the following is the null hypothesis, and which is the alternative hypothesis:
_____The sample proportion of 62 Yellowstone grizzly bears that enter their den for hibernation by the last day of November is 0.80.
_____The long-run proportion of Yellowstone grizzly bears that enter their den for hibernation by the last day of November is 0.80.
_____ The long-run proportion of Yellowstone grizzly bears that enter their den for hibernation by the last day of November is less than 0.80.
_____ The long-run proportion of Yellowstone grizzly bears that enter their den for hibernation by the last day of November is greater than 0.80.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
24
Research done in the mid 1980s indicated that 80% of grizzly bears in the greater ecosystem of Yellowstone National Park entered their den for hibernation by the last day of November. This has come into question as of late. Researchers have hypothesized that climate change has postponed bears entering hibernation until later in the season; that is, researchers believe that a smaller percentage of bears are entering their den for hibernation by the last day of November. Sixty-two Yellowstone grizzly bears were tracked via radio monitors, which allow scientists to pinpoint when the bears enter their dens with a high degree of accuracy. Of the sixty-two Yellowstone grizzly bears being tracked, forty-two entered their den for hibernation by the last day of November.
-What values would you enter for each of the following in the One Proportion applet to conduct a simulation-based hypothesis test with these data?
Probability of success: _______
Sample size: _______
Number of samples: _______
-What values would you enter for each of the following in the One Proportion applet to conduct a simulation-based hypothesis test with these data?
Probability of success: _______
Sample size: _______
Number of samples: _______

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
25
Research done in the mid 1980s indicated that 80% of grizzly bears in the greater ecosystem of Yellowstone National Park entered their den for hibernation by the last day of November. This has come into question as of late. Researchers have hypothesized that climate change has postponed bears entering hibernation until later in the season; that is, researchers believe that a smaller percentage of bears are entering their den for hibernation by the last day of November. Sixty-two Yellowstone grizzly bears were tracked via radio monitors, which allow scientists to pinpoint when the bears enter their dens with a high degree of accuracy. Of the sixty-two Yellowstone grizzly bears being tracked, forty-two entered their den for hibernation by the last day of November.
-A distribution of simulated "Number of successes," assuming the null hypothesis is true, is shown below. Circle the portion of the plot below that you would count to calculate the p-value.
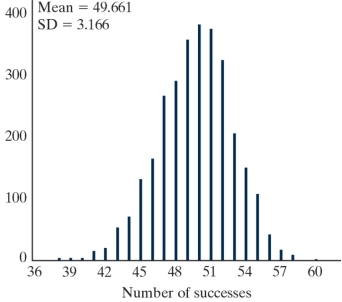
-A distribution of simulated "Number of successes," assuming the null hypothesis is true, is shown below. Circle the portion of the plot below that you would count to calculate the p-value.


Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
26
Research done in the mid 1980s indicated that 80% of grizzly bears in the greater ecosystem of Yellowstone National Park entered their den for hibernation by the last day of November. This has come into question as of late. Researchers have hypothesized that climate change has postponed bears entering hibernation until later in the season; that is, researchers believe that a smaller percentage of bears are entering their den for hibernation by the last day of November. Sixty-two Yellowstone grizzly bears were tracked via radio monitors, which allow scientists to pinpoint when the bears enter their dens with a high degree of accuracy. Of the sixty-two Yellowstone grizzly bears being tracked, forty-two entered their den for hibernation by the last day of November.
-How could we use coins, a spinner, or cards to simulate one of the samples in the above simulation? Select all that apply.
A) Flip a coin 62 times, where heads represents "hibernate by November 30." Count the number of heads in 62 flips.
B) Create a spinner with 80% shaded to represent "hibernate by November 30." Spin the spinner 62 times and count the number of times the spinner lands in the shaded area.
C) Have 8 black cards and 2 red cards where black represents "hibernate by November 30". Draw with replacement from the cards 62 times and count the number of times a black card is drawn.
D) Create a spinner with 68% shaded to represent "hibernate by November 30." Spin the spinner 62 times and count the number of times the spinner lands in the shaded area.
-How could we use coins, a spinner, or cards to simulate one of the samples in the above simulation? Select all that apply.
A) Flip a coin 62 times, where heads represents "hibernate by November 30." Count the number of heads in 62 flips.
B) Create a spinner with 80% shaded to represent "hibernate by November 30." Spin the spinner 62 times and count the number of times the spinner lands in the shaded area.
C) Have 8 black cards and 2 red cards where black represents "hibernate by November 30". Draw with replacement from the cards 62 times and count the number of times a black card is drawn.
D) Create a spinner with 68% shaded to represent "hibernate by November 30." Spin the spinner 62 times and count the number of times the spinner lands in the shaded area.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
27
Research done in the mid 1980s indicated that 80% of grizzly bears in the greater ecosystem of Yellowstone National Park entered their den for hibernation by the last day of November. This has come into question as of late. Researchers have hypothesized that climate change has postponed bears entering hibernation until later in the season; that is, researchers believe that a smaller percentage of bears are entering their den for hibernation by the last day of November. Sixty-two Yellowstone grizzly bears were tracked via radio monitors, which allow scientists to pinpoint when the bears enter their dens with a high degree of accuracy. Of the sixty-two Yellowstone grizzly bears being tracked, forty-two entered their den for hibernation by the last day of November.
-The simulation-based p-value for this test is 0.0153. Which of the following conclusions are correct? Select all that apply.
A) We have strong evidence against the null hypothesis.
B) We have strong evidence in favor of the null hypothesis.
C) We have strong evidence against the alternative hypothesis.
D) We have strong evidence in favor of the alternative hypothesis.
-The simulation-based p-value for this test is 0.0153. Which of the following conclusions are correct? Select all that apply.
A) We have strong evidence against the null hypothesis.
B) We have strong evidence in favor of the null hypothesis.
C) We have strong evidence against the alternative hypothesis.
D) We have strong evidence in favor of the alternative hypothesis.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
28
When using the One Proportion applet, the simulated null distribution should be centered around the observed sample proportion.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
29
If the sample size increases, the mean of the null distribution of sample proportions will decrease.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
30
If the sample size increases, the standard deviation of the null distribution of sample proportions will also increase.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
31
The first iPhone became available for public purchase in 2007. By 2010, approximately 30% of smartphone users in the US owned an iPhone. Several new companies have entered the smartphone market since then and the folks at Apple want to know how they are stacking up against their competition. In 2019, a representative sample of 529 smartphone users in the US showed that 47.4% use an Apple iOS device. Does it appear that Apple's share of the US smartphone market has increased since 2010?
-State the null and alternative hypotheses in proper notation.
A)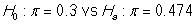
B)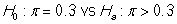
C)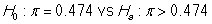
D)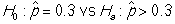
-State the null and alternative hypotheses in proper notation.
A)
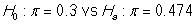
B)
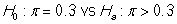
C)
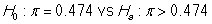
D)
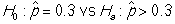

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
32
The first iPhone became available for public purchase in 2007. By 2010, approximately 30% of smartphone users in the US owned an iPhone. Several new companies have entered the smartphone market since then and the folks at Apple want to know how they are stacking up against their competition. In 2019, a representative sample of 529 smartphone users in the US showed that 47.4% use an Apple iOS device. Does it appear that Apple's share of the US smartphone market has increased since 2010?
-What is the value of the statistic and its proper notation in this study?
A)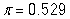
B)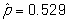
C)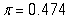
D)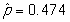
-What is the value of the statistic and its proper notation in this study?
A)
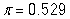
B)
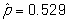
C)
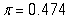
D)
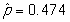

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
33
The first iPhone became available for public purchase in 2007. By 2010, approximately 30% of smartphone users in the US owned an iPhone. Several new companies have entered the smartphone market since then and the folks at Apple want to know how they are stacking up against their competition. In 2019, a representative sample of 529 smartphone users in the US showed that 47.4% use an Apple iOS device. Does it appear that Apple's share of the US smartphone market has increased since 2010?
-The following simulated null distribution of proportion of "Apple iOS users" that could happen by chance alone in a sample of 529 smartphone users was created with the One Proportion applet. Also, given are the mean and SD for this null distribution.
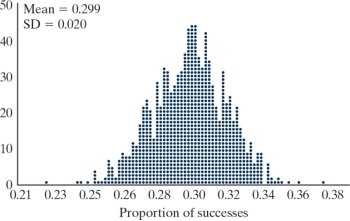 Calculate and report the standardized statistic.
Calculate and report the standardized statistic.
-The following simulated null distribution of proportion of "Apple iOS users" that could happen by chance alone in a sample of 529 smartphone users was created with the One Proportion applet. Also, given are the mean and SD for this null distribution.
 Calculate and report the standardized statistic.
Calculate and report the standardized statistic.
Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
34
The first iPhone became available for public purchase in 2007. By 2010, approximately 30% of smartphone users in the US owned an iPhone. Several new companies have entered the smartphone market since then and the folks at Apple want to know how they are stacking up against their competition. In 2019, a representative sample of 529 smartphone users in the US showed that 47.4% use an Apple iOS device. Does it appear that Apple's share of the US smartphone market has increased since 2010?
-Let X represent the value of your standardized statistic in 29. Select the best contextual interpretation of the value X.
A) On average, each simulated proportion of the US smartphone market which uses Apple iOS devices is X away from 0.299.
B) The probability of obtaining a sample proportion of 0.474 or something more extreme, assuming 30% of all US smartphone users use an Apple iOS device, is X.
C) The proportion of the US smartphone market that uses an Apple iOS device is X.
D) The 0.474 proportion of the US smartphone users sampled who use Apple iOS devices is X standard deviations above the 2010 Apple US market-share of 0.30.
-Let X represent the value of your standardized statistic in 29. Select the best contextual interpretation of the value X.
A) On average, each simulated proportion of the US smartphone market which uses Apple iOS devices is X away from 0.299.
B) The probability of obtaining a sample proportion of 0.474 or something more extreme, assuming 30% of all US smartphone users use an Apple iOS device, is X.
C) The proportion of the US smartphone market that uses an Apple iOS device is X.
D) The 0.474 proportion of the US smartphone users sampled who use Apple iOS devices is X standard deviations above the 2010 Apple US market-share of 0.30.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
35
The first iPhone became available for public purchase in 2007. By 2010, approximately 30% of smartphone users in the US owned an iPhone. Several new companies have entered the smartphone market since then and the folks at Apple want to know how they are stacking up against their competition. In 2019, a representative sample of 529 smartphone users in the US showed that 47.4% use an Apple iOS device. Does it appear that Apple's share of the US smartphone market has increased since 2010?
-Which of the following strength of evidence statements are correct, based on the standardized statistic in 29? Select all that apply. (If you didn't report a standardized statistic in 29, then use for this question.)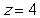
A) We have very strong evidence against the null hypothesis.
B) We have very strong evidence against the alternative hypothesis.
C) We have very strong evidence in favor of the null hypothesis.
D) We have very strong evidence in favor of the alternative hypothesis.
-Which of the following strength of evidence statements are correct, based on the standardized statistic in 29? Select all that apply. (If you didn't report a standardized statistic in 29, then use for this question.)
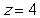
A) We have very strong evidence against the null hypothesis.
B) We have very strong evidence against the alternative hypothesis.
C) We have very strong evidence in favor of the null hypothesis.
D) We have very strong evidence in favor of the alternative hypothesis.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
36
The first iPhone became available for public purchase in 2007. By 2010, approximately 30% of smartphone users in the US owned an iPhone. Several new companies have entered the smartphone market since then and the folks at Apple want to know how they are stacking up against their competition. In 2019, a representative sample of 529 smartphone users in the US showed that 47.4% use an Apple iOS device. Does it appear that Apple's share of the US smartphone market has increased since 2010?
-What can we conclude about this study, based on the standardized statistic in 29? (If you didn't report a standardized statistic in 29, then use for this question.)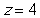
A) We have very strong evidence that Apple's share of the US smartphone market has remained the same since 2010.
B) We have very strong evidence that Apple's share of the US smartphone market has increased since 2010.
C) We do not have very strong evidence that Apple's share of the US smartphone market has increased since 2010.
D) We have very strong evidence that the proportion of the representative sample of 529 smartphone users in the US using an Apple iOS device is greater than 0.30.
-What can we conclude about this study, based on the standardized statistic in 29? (If you didn't report a standardized statistic in 29, then use for this question.)
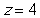
A) We have very strong evidence that Apple's share of the US smartphone market has remained the same since 2010.
B) We have very strong evidence that Apple's share of the US smartphone market has increased since 2010.
C) We do not have very strong evidence that Apple's share of the US smartphone market has increased since 2010.
D) We have very strong evidence that the proportion of the representative sample of 529 smartphone users in the US using an Apple iOS device is greater than 0.30.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
37
Match each standardized statistic value with its corresponding p-value:
-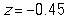 _______
_______
A) p-value = 0.009
B) p-value = 0.085
C) p-value = 0.653
-
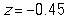 _______
_______A) p-value = 0.009
B) p-value = 0.085
C) p-value = 0.653

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
38
Match each standardized statistic value with its corresponding p-value:
-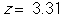 _______
_______
A) p-value = 0.010
B) p-value = 0.086
C) p-value = 0.654
-
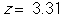 _______
_______A) p-value = 0.010
B) p-value = 0.086
C) p-value = 0.654

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
39
Match each standardized statistic value with its corresponding p-value:
-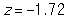 _______
_______
A) p-value = 0.011
B) p-value = 0.087
C) p-value = 0.655
-
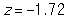 _______
_______A) p-value = 0.011
B) p-value = 0.087
C) p-value = 0.655

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
40
Do red uniform wearers tend to win more often than those wearing blue uniforms in Taekwondo matches where competitors are randomly assigned to wear either a red or blue uniform? In a sample of 80 Taekwondo matches, there were 45 matches where the red uniform wearer won. Given below is the simulated null distribution of proportion of "red wins" that could happen by chance alone in a sample of 80 matches. Also, given are the mean and SD for this null distribution. 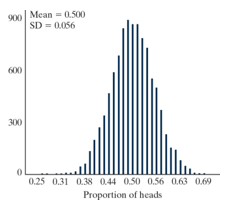
-What is the value of the standardized statistic?
A)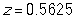
B)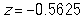
C)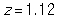
D)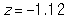

-What is the value of the standardized statistic?
A)
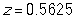
B)
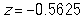
C)
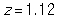
D)
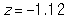

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
41
Do red uniform wearers tend to win more often than those wearing blue uniforms in Taekwondo matches where competitors are randomly assigned to wear either a red or blue uniform? In a sample of 80 Taekwondo matches, there were 45 matches where the red uniform wearer won. Given below is the simulated null distribution of proportion of "red wins" that could happen by chance alone in a sample of 80 matches. Also, given are the mean and SD for this null distribution. 
-Is there evidence that in Taekwondo matches, red uniform wearers tend to win more often than those wearing blue uniforms than would be expected by chance alone?
A) Yes, since 45 is greater than 30.
B) No, since we only observed 80 Taekwondo matches.
C) No, since the standardized statistic is between -1.5 and 1.5.
D) Yes, since the standardized statistic is between -1.5 and 1.5.

-Is there evidence that in Taekwondo matches, red uniform wearers tend to win more often than those wearing blue uniforms than would be expected by chance alone?
A) Yes, since 45 is greater than 30.
B) No, since we only observed 80 Taekwondo matches.
C) No, since the standardized statistic is between -1.5 and 1.5.
D) Yes, since the standardized statistic is between -1.5 and 1.5.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
42
The standardized statistic represents the number of standard deviations the observed statistic is above or below the hypothesized null value.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
43
If the standardized statistic is larger than 3, then the p-value will be larger than 0.10.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
44
A standardized statistic that is closer to zero provides stronger evidence against the null hypothesis.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
45
Research done in the mid 1980s indicated that 80% of grizzly bears in the greater ecosystem of Yellowstone National Park entered their den for hibernation by the last day of November. This has come into question as of late. Researchers have hypothesized that climate change has postponed bears entering hibernation until later in the season; that is, researchers believe that a smaller percentage of bears are entering their den for hibernation by the last day of November.
Sixty-two Yellowstone grizzly bears were tracked via radio monitors, which allow scientists to pinpoint when the bears enter their dens with a high degree of accuracy. Of the 62 Yellowstone grizzly bears being tracked, 42 entered their den for hibernation by the last day of November.
For each of the following sample results, circle whether the p-value would increase, decrease, or remain the same if we were to track another sample of Yellowstone grizzly bears.
-126 of 186 bears had entered their den for hibernation by the last day of November.
A) Increase
B) Decrease
C) Remain the same
Sixty-two Yellowstone grizzly bears were tracked via radio monitors, which allow scientists to pinpoint when the bears enter their dens with a high degree of accuracy. Of the 62 Yellowstone grizzly bears being tracked, 42 entered their den for hibernation by the last day of November.
For each of the following sample results, circle whether the p-value would increase, decrease, or remain the same if we were to track another sample of Yellowstone grizzly bears.
-126 of 186 bears had entered their den for hibernation by the last day of November.
A) Increase
B) Decrease
C) Remain the same

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
46
Research done in the mid 1980s indicated that 80% of grizzly bears in the greater ecosystem of Yellowstone National Park entered their den for hibernation by the last day of November. This has come into question as of late. Researchers have hypothesized that climate change has postponed bears entering hibernation until later in the season; that is, researchers believe that a smaller percentage of bears are entering their den for hibernation by the last day of November.
Sixty-two Yellowstone grizzly bears were tracked via radio monitors, which allow scientists to pinpoint when the bears enter their dens with a high degree of accuracy. Of the 62 Yellowstone grizzly bears being tracked, 42 entered their den for hibernation by the last day of November.
For each of the following sample results, circle whether the p-value would increase, decrease, or remain the same if we were to track another sample of Yellowstone grizzly bears.
-45 of 62 bears had entered their den for hibernation by the last day of November.
A) Increase
B) Decrease
C) Remain the same
Sixty-two Yellowstone grizzly bears were tracked via radio monitors, which allow scientists to pinpoint when the bears enter their dens with a high degree of accuracy. Of the 62 Yellowstone grizzly bears being tracked, 42 entered their den for hibernation by the last day of November.
For each of the following sample results, circle whether the p-value would increase, decrease, or remain the same if we were to track another sample of Yellowstone grizzly bears.
-45 of 62 bears had entered their den for hibernation by the last day of November.
A) Increase
B) Decrease
C) Remain the same

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
47
Research done in the mid 1980s indicated that 80% of grizzly bears in the greater ecosystem of Yellowstone National Park entered their den for hibernation by the last day of November. This has come into question as of late. Researchers have hypothesized that climate change has postponed bears entering hibernation until later in the season; that is, researchers believe that a smaller percentage of bears are entering their den for hibernation by the last day of November.
Sixty-two Yellowstone grizzly bears were tracked via radio monitors, which allow scientists to pinpoint when the bears enter their dens with a high degree of accuracy. Of the 62 Yellowstone grizzly bears being tracked, 42 entered their den for hibernation by the last day of November.
For each of the following sample results, circle whether the p-value would increase, decrease, or remain the same if we were to track another sample of Yellowstone grizzly bears.
-21 of 31 bears had entered their den for hibernation by the last day of November.
A) Increase
B) Decrease
C) Remain the same
Sixty-two Yellowstone grizzly bears were tracked via radio monitors, which allow scientists to pinpoint when the bears enter their dens with a high degree of accuracy. Of the 62 Yellowstone grizzly bears being tracked, 42 entered their den for hibernation by the last day of November.
For each of the following sample results, circle whether the p-value would increase, decrease, or remain the same if we were to track another sample of Yellowstone grizzly bears.
-21 of 31 bears had entered their den for hibernation by the last day of November.
A) Increase
B) Decrease
C) Remain the same

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
48
An environmental science teacher at a high school with a large population of students was curious whether the majority (more than half) of students at the school regularly recycle plastic bottles. The teacher selected a random sample of 146 students at the school to interview, then asked each student: "Do you recycle plastic bottles more often than you throw them in the trash?" (Yes/No). Suppose that 89 of the students answered "Yes".
-What is the parameter of interest for this study?
A) The proportion of the 146 students in the sample that would answer "Yes"
B) The proportion of all students at the school that would answer "Yes"
C) All students at the school
D) The true mean number of students at the school who would answer "Yes"
-What is the parameter of interest for this study?
A) The proportion of the 146 students in the sample that would answer "Yes"
B) The proportion of all students at the school that would answer "Yes"
C) All students at the school
D) The true mean number of students at the school who would answer "Yes"

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
49
An environmental science teacher at a high school with a large population of students was curious whether the majority (more than half) of students at the school regularly recycle plastic bottles. The teacher selected a random sample of 146 students at the school to interview, then asked each student: "Do you recycle plastic bottles more often than you throw them in the trash?" (Yes/No). Suppose that 89 of the students answered "Yes".
-What are the null and alternative hypotheses in appropriate notation?
A)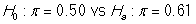
B)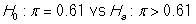
C)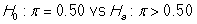
D)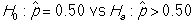
-What are the null and alternative hypotheses in appropriate notation?
A)
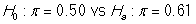
B)
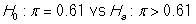
C)
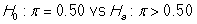
D)
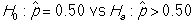

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
50
An environmental science teacher at a high school with a large population of students was curious whether the majority (more than half) of students at the school regularly recycle plastic bottles. The teacher selected a random sample of 146 students at the school to interview, then asked each student: "Do you recycle plastic bottles more often than you throw them in the trash?" (Yes/No). Suppose that 89 of the students answered "Yes".
-Use the One Proportion applet to calculate a p-value for this study.
-Use the One Proportion applet to calculate a p-value for this study.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
51
An environmental science teacher at a high school with a large population of students was curious whether the majority (more than half) of students at the school regularly recycle plastic bottles. The teacher selected a random sample of 146 students at the school to interview, then asked each student: "Do you recycle plastic bottles more often than you throw them in the trash?" (Yes/No). Suppose that 89 of the students answered "Yes".
-How could we use coins, a spinner, or cards to simulate one of the samples in the simulated null distribution? Select all that apply.
A) Flip a coin 146 times, where heads represents "answered Yes". Count the number of heads in 146 flips.
B) Create a spinner with 61% shaded to represent "answered Yes". Spin the spinner 146 times and count the number of times the spinner lands in the shaded area.
C) Have 5 black cards and 5 red cards where black represents "answered Yes". Draw with replacement from the cards 146 times and count the number of times a black card is drawn.
D) Create a spinner with 50% shaded to represent "answered Yes". Spin the spinner 146 times and count the number of times the spinner lands in the shaded area.
-How could we use coins, a spinner, or cards to simulate one of the samples in the simulated null distribution? Select all that apply.
A) Flip a coin 146 times, where heads represents "answered Yes". Count the number of heads in 146 flips.
B) Create a spinner with 61% shaded to represent "answered Yes". Spin the spinner 146 times and count the number of times the spinner lands in the shaded area.
C) Have 5 black cards and 5 red cards where black represents "answered Yes". Draw with replacement from the cards 146 times and count the number of times a black card is drawn.
D) Create a spinner with 50% shaded to represent "answered Yes". Spin the spinner 146 times and count the number of times the spinner lands in the shaded area.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
52
An environmental science teacher at a high school with a large population of students was curious whether the majority (more than half) of students at the school regularly recycle plastic bottles. The teacher selected a random sample of 146 students at the school to interview, then asked each student: "Do you recycle plastic bottles more often than you throw them in the trash?" (Yes/No). Suppose that 89 of the students answered "Yes".
-Would you consider the results of this test to be statistically significant?
A) Yes, because the simulated distribution is not centered on the observed statistic.
B) No, because the results are unlikely to occur by random chance alone.
C) No, because the simulation proves that the null hypothesis is true.
D) Yes, because the results are unlikely to occur by random chance alone.
-Would you consider the results of this test to be statistically significant?
A) Yes, because the simulated distribution is not centered on the observed statistic.
B) No, because the results are unlikely to occur by random chance alone.
C) No, because the simulation proves that the null hypothesis is true.
D) Yes, because the results are unlikely to occur by random chance alone.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
53
An environmental science teacher at a high school with a large population of students was curious whether the majority (more than half) of students at the school regularly recycle plastic bottles. The teacher selected a random sample of 146 students at the school to interview, then asked each student: "Do you recycle plastic bottles more often than you throw them in the trash?" (Yes/No). Suppose that 89 of the students answered "Yes".
-The teacher sampled 300 students instead of 146.
A) Stronger evidence against the null hypothesis
B) Weaker evidence against the null hypothesis
C) The same amount of evidence against the null hypothesis
D) Cannot be determined from the information given
-The teacher sampled 300 students instead of 146.
A) Stronger evidence against the null hypothesis
B) Weaker evidence against the null hypothesis
C) The same amount of evidence against the null hypothesis
D) Cannot be determined from the information given

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
54
An environmental science teacher at a high school with a large population of students was curious whether the majority (more than half) of students at the school regularly recycle plastic bottles. The teacher selected a random sample of 146 students at the school to interview, then asked each student: "Do you recycle plastic bottles more often than you throw them in the trash?" (Yes/No). Suppose that 89 of the students answered "Yes".
-The sample proportion of students who said "Yes" was 0.75 instead of 0.61.
A) Stronger evidence against the null hypothesis
B) Weaker evidence against the null hypothesis
C) The same amount of evidence against the null hypothesis
D) Cannot be determined from the information given
-The sample proportion of students who said "Yes" was 0.75 instead of 0.61.
A) Stronger evidence against the null hypothesis
B) Weaker evidence against the null hypothesis
C) The same amount of evidence against the null hypothesis
D) Cannot be determined from the information given

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
55
An environmental science teacher at a high school with a large population of students was curious whether the majority (more than half) of students at the school regularly recycle plastic bottles. The teacher selected a random sample of 146 students at the school to interview, then asked each student: "Do you recycle plastic bottles more often than you throw them in the trash?" (Yes/No). Suppose that 89 of the students answered "Yes".
-The sample proportion of students who said "Yes" was 0.55 instead of 0.61.
A) Stronger evidence against the null hypothesis
B) Weaker evidence against the null hypothesis
C) The same amount of evidence against the null hypothesis
D) Cannot be determined from the information given
-The sample proportion of students who said "Yes" was 0.55 instead of 0.61.
A) Stronger evidence against the null hypothesis
B) Weaker evidence against the null hypothesis
C) The same amount of evidence against the null hypothesis
D) Cannot be determined from the information given

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
56
An environmental science teacher at a high school with a large population of students was curious whether the majority (more than half) of students at the school regularly recycle plastic bottles. The teacher selected a random sample of 146 students at the school to interview, then asked each student: "Do you recycle plastic bottles more often than you throw them in the trash?" (Yes/No). Suppose that 89 of the students answered "Yes".
-We want to know if the proportion of students at the school that would have said "Yes" differed from 0.5 rather than was greater than 0.5.
A) Stronger evidence against the null hypothesis
B) Weaker evidence against the null hypothesis
C) The same amount of evidence against the null hypothesis
D) Cannot be determined from the information given
-We want to know if the proportion of students at the school that would have said "Yes" differed from 0.5 rather than was greater than 0.5.
A) Stronger evidence against the null hypothesis
B) Weaker evidence against the null hypothesis
C) The same amount of evidence against the null hypothesis
D) Cannot be determined from the information given

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
57
An environmental science teacher at a high school with a large population of students was curious whether the majority (more than half) of students at the school regularly recycle plastic bottles. The teacher selected a random sample of 146 students at the school to interview, then asked each student: "Do you recycle plastic bottles more often than you throw them in the trash?" (Yes/No). Suppose that 89 of the students answered "Yes".
-We want to know if less than half of all students at the school would have said "Yes" rather than greater than half.
A) Stronger evidence against the null hypothesis
B) Weaker evidence against the null hypothesis
C) The same amount of evidence against the null hypothesis
D) Cannot be determined from the information given
-We want to know if less than half of all students at the school would have said "Yes" rather than greater than half.
A) Stronger evidence against the null hypothesis
B) Weaker evidence against the null hypothesis
C) The same amount of evidence against the null hypothesis
D) Cannot be determined from the information given

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
58
For each of the following scenarios, determine whether the alternative hypothesis would be one-sided or two-sided.
-A recent Gallup poll reported that 77% of Americans are at least 'somewhat' confident in the government's ability to handle a coronavirus outbreak. A student researcher is interested if students at their university are more skeptical (less likely to feel confident) than what was reported in the Gallup poll.
A) one-sided
B) two-sided
-A recent Gallup poll reported that 77% of Americans are at least 'somewhat' confident in the government's ability to handle a coronavirus outbreak. A student researcher is interested if students at their university are more skeptical (less likely to feel confident) than what was reported in the Gallup poll.
A) one-sided
B) two-sided

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
59
For each of the following scenarios, determine whether the alternative hypothesis would be one-sided or two-sided.
-In 2010, it was believed that 18% of American cell phone owners do their browsing on their phone rather than a computer or other device. A recent survey conducted on a representative sample of 621 American cell phone owners showed 22% now do their browsing on their mobile device. Do these data provide evidence that the proportion of American cell phone owners who do their browsing on their phones rather than their computers or other devices has changed in the last 10 years?
A) one-sided
B) two-sided
-In 2010, it was believed that 18% of American cell phone owners do their browsing on their phone rather than a computer or other device. A recent survey conducted on a representative sample of 621 American cell phone owners showed 22% now do their browsing on their mobile device. Do these data provide evidence that the proportion of American cell phone owners who do their browsing on their phones rather than their computers or other devices has changed in the last 10 years?
A) one-sided
B) two-sided

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
60
For each of the following scenarios, determine whether the alternative hypothesis would be one-sided or two-sided.
-According to enrollment data in 2016, 55% of undergraduates at a state university were out-of-state students. Your statistics instructor wonders if the proportion of out-of-state undergraduates at this university has changed. She surveys her students (145 students). The results of the sample showed that 73 were out-of-state students.
A) one-sided
B) two-sided
-According to enrollment data in 2016, 55% of undergraduates at a state university were out-of-state students. Your statistics instructor wonders if the proportion of out-of-state undergraduates at this university has changed. She surveys her students (145 students). The results of the sample showed that 73 were out-of-state students.
A) one-sided
B) two-sided

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
61
For each of the following scenarios, determine whether the alternative hypothesis would be one-sided or two-sided.
-Retired professional tennis players Martina Navratilova, Monica Seles, John McEnroe, and Jimmy Connors are all left-handed. About 10% of the general population is left-handed. Researchers are interested if the proportion of professional tennis players that are left-handed is larger than that of the general population.
A) one-sided
B) two-sided
-Retired professional tennis players Martina Navratilova, Monica Seles, John McEnroe, and Jimmy Connors are all left-handed. About 10% of the general population is left-handed. Researchers are interested if the proportion of professional tennis players that are left-handed is larger than that of the general population.
A) one-sided
B) two-sided

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
62
The official four-year graduation rate among US colleges and universities is 57.6%. Suppose a researcher takes a random sample of 100 college students and tracks their progress through school to determine whether each student graduates in four years or not. Which of the following do you know to be true? Select all that apply.
A) If many samples of 100 students were taken, the distribution of the sample proportions would be bell-shaped and symmetric.
B) If many samples of 100 students were taken, the distribution of the sample proportions would be centered at 0.576.
C) The sample proportion collected by the researcher would be 0.576.
D) If many samples of 100 students were taken, the standard deviation of the sample proportions would be 0.049.
A) If many samples of 100 students were taken, the distribution of the sample proportions would be bell-shaped and symmetric.
B) If many samples of 100 students were taken, the distribution of the sample proportions would be centered at 0.576.
C) The sample proportion collected by the researcher would be 0.576.
D) If many samples of 100 students were taken, the standard deviation of the sample proportions would be 0.049.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
63
A study conducted by the National Center for Health Statistics as part of the Center for Disease Control and Prevention (CDC) found that, as of 2015-2016, 39.6% of Americans over the age of 20 fit the medical definition of being obese (BMI of 30 or higher). A city known for its plentiful outdoor opportunities believes that number is lower among its residents. A representative sample of 80 city residents is collected and the BMI calculated for each (based on reported height and weight). The variable of interest is whether the resident fit the medical definition of obese. The study found 22 people in the sample fit the medical definition of obese.
-Is a theory-based method appropriate for these data?
A) Yes, because a representative sample was collected.
B) Yes, because there were 22 people defined as obese and 58 people not defined as obese in the sample, and both of these values are greater than 10.
C) No, because the researcher did not collect a random sample.
D) No, because the national obesity rate is not 0.5.
-Is a theory-based method appropriate for these data?
A) Yes, because a representative sample was collected.
B) Yes, because there were 22 people defined as obese and 58 people not defined as obese in the sample, and both of these values are greater than 10.
C) No, because the researcher did not collect a random sample.
D) No, because the national obesity rate is not 0.5.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
64
A study conducted by the National Center for Health Statistics as part of the Center for Disease Control and Prevention (CDC) found that, as of 2015-2016, 39.6% of Americans over the age of 20 fit the medical definition of being obese (BMI of 30 or higher). A city known for its plentiful outdoor opportunities believes that number is lower among its residents. A representative sample of 80 city residents is collected and the BMI calculated for each (based on reported height and weight). The variable of interest is whether the resident fit the medical definition of obese. The study found 22 people in the sample fit the medical definition of obese.
-Identify which of the following is the null hypothesis.
A) The sample proportion of 80 city residents that fit the medical definition of obese is equal to 0.396.
B) The long-run proportion of city residents that fit the medical definition of obese is equal to 0.396.
C) The long-run proportion of all Americans over the age of 20 that fit the medical definition of obese is equal to 0.396.
D) The sample proportion of 80 city residents that fit the medical definition of obese is equal to 0.275.
-Identify which of the following is the null hypothesis.
A) The sample proportion of 80 city residents that fit the medical definition of obese is equal to 0.396.
B) The long-run proportion of city residents that fit the medical definition of obese is equal to 0.396.
C) The long-run proportion of all Americans over the age of 20 that fit the medical definition of obese is equal to 0.396.
D) The sample proportion of 80 city residents that fit the medical definition of obese is equal to 0.275.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
65
A study conducted by the National Center for Health Statistics as part of the Center for Disease Control and Prevention (CDC) found that, as of 2015-2016, 39.6% of Americans over the age of 20 fit the medical definition of being obese (BMI of 30 or higher). A city known for its plentiful outdoor opportunities believes that number is lower among its residents. A representative sample of 80 city residents is collected and the BMI calculated for each (based on reported height and weight). The variable of interest is whether the resident fit the medical definition of obese. The study found 22 people in the sample fit the medical definition of obese.
-Identify the correct alternative hypothesis.
A)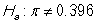
B)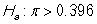
C)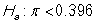
D)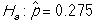
-Identify the correct alternative hypothesis.
A)
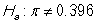
B)
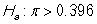
C)
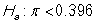
D)
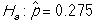

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
66
A study conducted by the National Center for Health Statistics as part of the Center for Disease Control and Prevention (CDC) found that, as of 2015-2016, 39.6% of Americans over the age of 20 fit the medical definition of being obese (BMI of 30 or higher). A city known for its plentiful outdoor opportunities believes that number is lower among its residents. A representative sample of 80 city residents is collected and the BMI calculated for each (based on reported height and weight). The variable of interest is whether the resident fit the medical definition of obese. The study found 22 people in the sample fit the medical definition of obese.
-Select the appropriate method of calculating the standard deviation of the sample proportions under the null hypothesis.
A)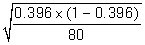
B)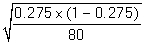
C)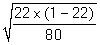
D)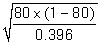
-Select the appropriate method of calculating the standard deviation of the sample proportions under the null hypothesis.
A)
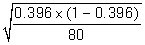
B)
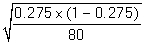
C)
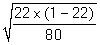
D)
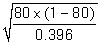

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
67
A study conducted by the National Center for Health Statistics as part of the Center for Disease Control and Prevention (CDC) found that, as of 2015-2016, 39.6% of Americans over the age of 20 fit the medical definition of being obese (BMI of 30 or higher). A city known for its plentiful outdoor opportunities believes that number is lower among its residents. A representative sample of 80 city residents is collected and the BMI calculated for each (based on reported height and weight). The variable of interest is whether the resident fit the medical definition of obese. The study found 22 people in the sample fit the medical definition of obese.
-Let 'A' represent your answer from 60. Which of the following displays the correct method of calculating the standardized statistic?
A)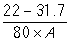
B)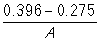
C)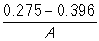
D)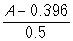
-Let 'A' represent your answer from 60. Which of the following displays the correct method of calculating the standardized statistic?
A)
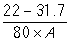
B)
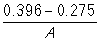
C)
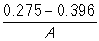
D)
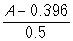

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
68
A study conducted by the National Center for Health Statistics as part of the Center for Disease Control and Prevention (CDC) found that, as of 2015-2016, 39.6% of Americans over the age of 20 fit the medical definition of being obese (BMI of 30 or higher). A city known for its plentiful outdoor opportunities believes that number is lower among its residents. A representative sample of 80 city residents is collected and the BMI calculated for each (based on reported height and weight). The variable of interest is whether the resident fit the medical definition of obese. The study found 22 people in the sample fit the medical definition of obese.
-The standardized statistic is equal to -2.213. Interpret this value in the context of the problem.
A) On average, each simulated sample proportion of residents that fit the medical definition of obese is 2.213 standard deviations away from 0.396.
B) The probability of obtaining a sample proportion of 0.275 or something more extreme, assuming 39.6% of all city residents fit the medical definition of obese, is 0.02213.
C) The observed sample proportion of city residents that fit the medical definition of obese, 0.275, is 2.213 standard deviations below the hypothesized proportion 0.396.
D) The hypothesized proportion of city residents that fit the medical definition of obese, 0.396, is 2.213 standard deviations below the sample proportion 0.275.
-The standardized statistic is equal to -2.213. Interpret this value in the context of the problem.
A) On average, each simulated sample proportion of residents that fit the medical definition of obese is 2.213 standard deviations away from 0.396.
B) The probability of obtaining a sample proportion of 0.275 or something more extreme, assuming 39.6% of all city residents fit the medical definition of obese, is 0.02213.
C) The observed sample proportion of city residents that fit the medical definition of obese, 0.275, is 2.213 standard deviations below the hypothesized proportion 0.396.
D) The hypothesized proportion of city residents that fit the medical definition of obese, 0.396, is 2.213 standard deviations below the sample proportion 0.275.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
69
A study conducted by the National Center for Health Statistics as part of the Center for Disease Control and Prevention (CDC) found that, as of 2015-2016, 39.6% of Americans over the age of 20 fit the medical definition of being obese (BMI of 30 or higher). A city known for its plentiful outdoor opportunities believes that number is lower among its residents. A representative sample of 80 city residents is collected and the BMI calculated for each (based on reported height and weight). The variable of interest is whether the resident fit the medical definition of obese. The study found 22 people in the sample fit the medical definition of obese.
-Once more, let 'A' represent your answer from 60. How should the p-value be calculated for this test? Select all that apply.
A) Find the area below the standardized statistic on the Standard Normal distribution.
B) Find the area below 0.275 on a Normal distribution centered at the null value with standard deviation
C) Find the proportion of samples at or below 0.275 on a simulated null distribution.
D) Find the area below A on a Standard Normal distribution.
-Once more, let 'A' represent your answer from 60. How should the p-value be calculated for this test? Select all that apply.
A) Find the area below the standardized statistic on the Standard Normal distribution.
B) Find the area below 0.275 on a Normal distribution centered at the null value with standard deviation
C) Find the proportion of samples at or below 0.275 on a simulated null distribution.
D) Find the area below A on a Standard Normal distribution.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
70
The World Health Organization reports that the SARS (Severe Acute Respiratory Syndrome) outbreak in 2003 resulted in 8098 probable cases reported, 774 of which were fatalities. A student who is planning to travel to Vietnam is concerned about another virus outbreak and would like to use data on how Vietnam handled SARS cases as a gauge for how well its health care system would handle another virus outbreak. The student plans to test if the fatality rate in Vietnam from SARS is different from the global fatality rate. Of the 89 SARS cases reported in Vietnam in 2003, 5 people died. The student analyzes these data in two ways:
Method 1: The theory-based p-value was calculated to be 0.2061.
Method 2: The simulation-based p-value was calculated to be 0.2797.
Which p-value is most valid?
A) The theory-based p-value, since the p-value is calculated by finding the exact area under a Normal distribution.
B) The theory-based p-value, since there are over 10 "failures" (people who survived SARS).
C) The simulation-based p-value, since there are only 5 "successes" (people who died from SARS).
D) The simulation-based p-value, since it simulates thousands of samples.
Method 1: The theory-based p-value was calculated to be 0.2061.
Method 2: The simulation-based p-value was calculated to be 0.2797.
Which p-value is most valid?
A) The theory-based p-value, since the p-value is calculated by finding the exact area under a Normal distribution.
B) The theory-based p-value, since there are over 10 "failures" (people who survived SARS).
C) The simulation-based p-value, since there are only 5 "successes" (people who died from SARS).
D) The simulation-based p-value, since it simulates thousands of samples.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
71
When President Trump took office in 2016, a Gallup poll reported that 55% of Americans supported stricter laws covering the sale of firearms. In 2020, the same poll was conducted on a representative sample of 943 Americans, and 64% of those surveyed supported stricter laws covering the sale of firearms. Has the percent of Americans supporting stricter laws covering the sale of firearms increased from 2016?
-Which hypothesis testing method is appropriate for this study?
A) Theory-based test
B) Simulation-based test
C) Either method is appropriate
D) Neither method is appropriate
-Which hypothesis testing method is appropriate for this study?
A) Theory-based test
B) Simulation-based test
C) Either method is appropriate
D) Neither method is appropriate

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
72
When President Trump took office in 2016, a Gallup poll reported that 55% of Americans supported stricter laws covering the sale of firearms. In 2020, the same poll was conducted on a representative sample of 943 Americans, and 64% of those surveyed supported stricter laws covering the sale of firearms. Has the percent of Americans supporting stricter laws covering the sale of firearms increased from 2016?
-Fill in the appropriate inputs to the Theory-Based Inference applet to conduct a theory-based test for this scenario.
n: _______
count: _______
 _______
_______
-Fill in the appropriate inputs to the Theory-Based Inference applet to conduct a theory-based test for this scenario.
n: _______
count: _______
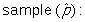 _______
_______
Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
73
When President Trump took office in 2016, a Gallup poll reported that 55% of Americans supported stricter laws covering the sale of firearms. In 2020, the same poll was conducted on a representative sample of 943 Americans, and 64% of those surveyed supported stricter laws covering the sale of firearms. Has the percent of Americans supporting stricter laws covering the sale of firearms increased from 2016?
-Fill in the blanks to enter the appropriate hypotheses into the Theory-Based Inference applet.
H0:? = ______ (B1)
HS:? ______ (DD) ______ (B3)
Drop-down (DD) options:
• ?
• <
• >
-Fill in the blanks to enter the appropriate hypotheses into the Theory-Based Inference applet.
H0:? = ______ (B1)
HS:? ______ (DD) ______ (B3)
Drop-down (DD) options:
• ?
• <
• >

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
74
When President Trump took office in 2016, a Gallup poll reported that 55% of Americans supported stricter laws covering the sale of firearms. In 2020, the same poll was conducted on a representative sample of 943 Americans, and 64% of those surveyed supported stricter laws covering the sale of firearms. Has the percent of Americans supporting stricter laws covering the sale of firearms increased from 2016?
-Use the Theory-Based Inference applet to compute the standardized statistic and p-value for this study.
standardized statistic = ______
p-value = _____
-Use the Theory-Based Inference applet to compute the standardized statistic and p-value for this study.
standardized statistic = ______
p-value = _____

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck
75
A simulated distribution of sample proportions will always be approximately normal.

Unlock Deck
Unlock for access to all 75 flashcards in this deck.
Unlock Deck
k this deck


