Deck 4: Linear Programming: Applications and Solutions

Question 1

A two-variable linear programming problem cannot be solved by the simplex method.

Answer 1

False

Question 2

A two-variable linear programming problem can only be solved by the simplex method.

Answer 2

False

Question 3

Graphical simplex is a good alternative to simplex method for all linear programming problems.

Answer 3

False

Question 4

In a linear programming problem with an equality constraint and an optimal solution, if the equality constraint is changed to an inequality constraint, all other things remaining the same, the problem may become infeasible.

Question 5

In a linear programming problem with an equality constraint and an optimal solution, if the equality constraint is changed to an inequality constraint, all other things remaining the same, the problem may become unbounded.

Question 6

In a linear programming problem with an inequality constraint and an optimal solution, if the inequality constraint is changed to an inequality constraint, all other things remaining the same, the problem may become infeasible.

Question 7

In a linear programming problem with an inequality constraint and an optimal solution, if the inequality constraint is changed to an inequality constraint, all other things remaining the same, the problem may become unbounded.

Question 8

If the sale of the first 10 units of a product gives a profit of $\$ 10.00$ per unit and every additional unit sold gives a profit of $\$ 15.00$ per unit, the situation cannot be modeled easily as a linear program.

Question 9

SUMPRODUCT command of excel can be used for multiplying elements of two arrays of unequal lengths, though it is usually used for arrays of equal length.

Question 10

In a linear program, if a constraint is of the form $\leq$ , solutions that make the constraint exactly equal will also be allowed.

Question 11

In a linear program, if a constraint is of the equality type (=), then solutions that make the constraint $<$ will also be allowed (that is, these solutions will also be feasible).

Question 12

In a linear program, with the decision variables corresponding to level of sales of three products, and the objective of maximizing total contribution, selling price may be used as objective function coefficients even if the net contribution per unit is given.

Question 13

In a linear program, if a constraint simply relates the ratio of constant multiples of two decision variables to a constant through $=, \geq$ , or $\leq$ , then the constraint can always be converted to a linear constraint.

Question 14

In a linear program, if a constraint simply relates the ratio of linear expressions involving decision variables to a constant through $=$ , $\geq$ , or $\leq$ , then the constraint can always be converted to a linear constraint.

Question 15

In a linear program, if a constraint simply relates the ratio of linear expressions involving decision variables to another decision variable through $=, \geq$ , or $\leq$ , then the constraint can always be converted to a linear constraint.

Question 16

In a linear program, if the constraint simply relates the ratio of constant multiples of two decision variables to another decision variable through $=, \geq$ , or $\leq$ , then the constraint can always be converted to a linear constraint.

Question 17

If a linear program does not have a feasible solution, adding one more constraint to the linear program, but keeping all other things unchanged, may make the problem feasible.

Question 18

If a linear program does not have a feasible solution, removing one constraint from the linear program, but keeping all other things unchanged, may make the problem feasible.

Question 19

If a linear program is unbounded, adding one more constraint to the linear program, but keeping all other things unchanged, may make the problem bounded and hence have an optimal solution.

Question 20

If a linear program is unbounded, removing one constraint from the linear program, but keeping all other things unchanged, may make the problem bounded and hence have an optimal solution.

Question 21

All linear programming formulations with minimize objective function can be converted into an equivalent problem with maximize objective function by simply multiplying the objective function expression by -1 and leaving constraints unchanged.

Question 22

In any linear programming problem with an equality constraint, an equivalent formulation can be obtained by simply replacing the equality constraint with a pair of inequality constraints obtained by serially replacing the equality sign of the constraint with $\pounds$ and by ${ }^{3}$ signs, leaving all other things unchanged.

Question 23

In using the Solver package to solve a linear programming problem, the non-negativity constraints must be explicitly specified as part of the constraint set.

Question 24

In a typical diet problem formulation, suppose that drinking milk and eating carrots together added more nutritional value due to the interaction of the two foods in the digestive process than doing the exact same things 3 hours apart. This would still lend itself to linear programming formulation.

Question 25

In a typical diet problem formulation, suppose that carrots cost $\$ 1.00$ per pound if you buy one pound or less and only $\$ 0.70$ per pound if you purchase more than one pound. One of the components of the formulation is to minimize cost of the diet. This would still lend itself to linear programming formulation.

Question 26

A linear programming formulation, which is unbounded, cannot have a feasible solution.

Question 27

A linear programming formulation, which is unbounded, may become bounded and have an optimal solution by the addition of a constraint.

Question 28

A linear programming formulation, which has an optimal solution, cannot become unbounded by the addition of a single constraint.

Question 29

A linear programming formulation, which has an optimal solution, cannot become infeasible by the addition of a single constraint.

Question 30

A linear programming formulation, which has an optimal solution, can become unbounded by removal of a single constraint.

Question 31

A linear programming formulation, which has a unique optimal solution, cannot have multiple optimal solutions by the addition of a single constraint.

Question 32

A linear programming formulation, which has a unique optimal solution, can have multiple optimal solutions for a different objective function.

Question 33

A linear programming formulation, which has a unique optimal solution, can be infeasible for a different objective function.

Question 34

A linear programming formulation, which has a unique optimal solution, can be unbounded for a different objective function.

Question 35

In using the Solver package to solve a linear programming problem, the decision variables are assigned to the

A) target cell/s
B) changing cell/s
C) constraint cells
D) variable cells

Question 36

In using the Solver package to solve a linear programming problem, the objective function expression and its value are defined in the

A) target cell/s
B) changing cell/s
C) constraint cells
D) variable cells

Question 37

Problem $\mathrm{A}$ is a given formulation of a linear program with an optimal solution. Problem $\mathrm{B}$ is a formulation obtained by multiplying the objective function of Problem A by a positive constant and leaving all other things unchanged. Problems A and B will have

A) the same optimal solution and same objective function value
B) the same optimal solution but different objective function values
C) different optimal solutions but same objective function value
D) different optimal solutions and different objective function values
E) same or different solution profile depending on the role of the constraint in the solutions

Question 38

Problem A is a given formulation of a linear program with an optimal solution. Problem B is a formulation obtained by multiplying the objective function of Problem A by a negative constant and leaving all other things unchanged. Problems A and B may have

A) the same optimal solution and same objective function value
B) the same optimal solution but different objective function values
C) different optimal solutions but same objective function value
D) different optimal solutions and different objective function values
E) same or different solution profile depending on the role of the constraint in the solutions.

Question 39

Problem A is a given formulation of a linear program with an optimal solution. Problem B is a formulation obtained by multiplying constraint 1 of Problem A by a positive constant and leaving all other things unchanged. Problems A and B will have

A) the same optimal solution and same objective function value
B) the same optimal solution but different objective function values
C) different optimal solutions but same objective function value
D) different optimal solutions and different objective function values
E) same or different solution profile depending on the role of the constraint in the solutions

Question 40

Problem $A$ is a given formulation of a linear program with an optimal solution. Problem $B$ is a formulation obtained by multiplying all constraints of Problem A by a positive constant and leaving all other things unchanged. Problems A and B will have

A) the same optimal solution and same objective function value
B) the same optimal solution but different objective function values
C) different optimal solutions but same objective function value
D) different optimal solutions and different objective function values
E) same or different solution profile depending on the role of the constraint in the solutions

Question 41

Problem $A$ is a given formulation of a linear program with an optimal solution. Problem $B$ is a formulation obtained by adding a constant to the objective function of Problem A and leaving all other things unchanged. Problems A and B will have

A) the same optimal solution and same objective function value
B) the same optimal solution but different objective function values
C) different optimal solutions but same objective function value
D) different optimal solutions and different objective function values
E) same or different solution profile depending on the role of the constraint in the solutions

Question 42

Problem $\mathrm{A}$ is a given formulation of a linear program with an optimal solution. Problem $\mathrm{B}$ is a formulation obtained by multiplying constraint 1 of Problem A by a negative constant and leaving all other things unchanged. Problems A and B may have

A) the same optimal solution and same objective function value
B) the same optimal solution but different objective function values
C) different optimal solutions but same objective function value
D) different optimal solutions and different objective function values
E) same or different solution profile depending on the role of the constraint in the solutions

Question 43

Problem $A$ is a given formulation of a linear program with an optimal solution. Problem $B$ is a formulation obtained by adding a constant to the right hand side of Constraint 1 of Problem A and leaving all other things unchanged. Problems A and B will have

A) the same optimal solution and same objective function value
B) the same optimal solution but different objective function values
C) different optimal solutions but same objective function value
D) different optimal solutions and different objective function values
E) same or different solution profile depending on the role of the constraint in the solutions

Question 44

Problem $\mathrm{A}$ is a given formulation of a linear program with an optimal solution. Problem $\mathrm{B}$ is a formulation obtained from Problem A by omitting the non-negativity constraints and leaving all other things unchanged. Problems A and B will have

A) the same optimal solution and same objective function value
B) the same optimal solution but different objective function values
C) different optimal solutions but same objective function value
D) different optimal solutions and different objective function values
E) same or different solution profile depending on the role of the constraints in the solutions

Question 45

Problem $\mathrm{A}$ is a given formulation of a linear program with an optimal solution. Problem $\mathrm{B}$ is a formulation obtained from Problem A by omitting constraint 1 of Problem A and leaving all other things unchanged. Problems A and B will have

A) the same optimal solution and same objective function value
B) the same optimal solution but different objective function values
C) different optimal solutions but same objective function value
D) different optimal solutions and different objective function values
E) same or different solution profile depending on the role of the constraints in the solutions

Question 46

Problem $\mathrm{A}$ is a given formulation of a linear program with an optimal solution. Problem $\mathrm{B}$ is a formulation obtained from Problem A by dropping exactly one variable and leaving all other things unchanged. Problems A and B will have

A) the same optimal solution and same objective function value
B) the same optimal solution but different objective function values
C) different optimal solutions but same objective function value
D) different optimal solutions and different objective function values
E) same or different solution profile depending on the role of the constraints in the solutions

Question 47

Problem $\mathrm{A}$ is a given formulation of a linear program with an optimal solution and exactly one equality constraint. Problem B is a formulation obtained from Problem A by replacing the equality constraint with a pair of inequality constraints obtained by serially replacing the equality sign of the constraint with $\pounds$ and ${ }^{3}$ signs, leaving all other things unchanged. Problems A and B will have

A) the same optimal solution and same objective function value
B) the same optimal solution but different objective function values
C) different optimal solutions but same objective function value
D) different optimal solutions and different objective function values
E) same or different solution profile depending on the role of the constraints in the solutions

Question 48

Problem $\mathrm{A}$ is a given formulation of a linear program with an optimal solution, and its constraint 1 is $\pounds$ type. Problem B is a formulation obtained from Problem A by replacing the $\pounds$ constraint with an equality constraint and leaving all other things unchanged. Problems A and B will have

A) the same optimal solution and same objective function value
B) the same optimal solution but different objective function values
C) different optimal solutions but same objective function value
D) different optimal solutions and different objective function values
E) same or different solution profile depending on the role of the constraints in the solutions

Question 49

Problem A is a given formulation of a linear program with an optimal solution. Problem B is a formulation obtained from Problem A by adding a redundant constraint, leaving all other things unchanged. Problems A and B will have

A) the same optimal solution and same objective function value
B) the same optimal solution but different objective function values
C) different optimal solutions but same objective function value
D) different optimal solutions and different objective function values
E) same or different solution profile depending on the role of the constraints in the solutions

Question 50

Problem $A$ is a given formulation of a linear program with an optimal solution. Problem B is a formulation obtained from Problem A by adding a constraint, and leaving all other things unchanged. Problems A and B will have

A) the same optimal solution and same objective function value
B) the same optimal solution but different objective function values
C) different optimal solutions but same objective function value
D) different optimal solutions and different objective function values
E) same or different solution profile depending on the role of the constraint in Problem B

Question 51

In formulating a coffee blending problem where there are three types of coffee beans, the objective is to find a recipe to make 1 pound of blended coffee that satisfies a set of properties at the least cost. The decision variables are $X_{1}, X_{2}$ , and $X_{3}$ , representing pounds (actually fractional pounds) of coffee beans used per pound of blended coffee. One of the constraints of the problem will be

A) $X_{1}+X_{2}+X_{3}<1.0$
B) $X_{1}+X_{2}+X_{3}>1.0$
C) $X_{1}+X_{2}+X_{3}=1.0$
D) no such constraint is required

Question 52

In formulating a coffee blending problem where there are three types of coffee beans, the objective is to find a recipe to make 1 pound of blended coffee that satisfies a set of properties at the least cost. The decision variables are $X_{1}, X_{2}$ , and ${ }^{X_{3}}$ , representing pounds (actually fractional pounds) of coffee beans used per pound of blended coffee. Suppose that bitterness is a property measured as an index from 1 to 6 and a blend's bitterness is given by the weighted average (using the weight fraction of each beans in the blend as the weight) of the bitterness of individual beans going into the blend. Suppose that the bitterness indices for the three beans are respectively 2, 4, and 5 . A blend with bitterness in the range 3 to 4.5 is most desirable. The appropriate constraint/s will be

A) $2 X_{1}+4 X_{2}+5 X_{3} \geq 3.0$
B) $2 X_{1}+4 X_{2}+5 X_{3} \leq 4.5$
C) $2 X_{1}+4 X_{2}+5 X_{3} \geq 3.0$ and $2 X_{1}+4 X_{2}+5 X_{3} \leq 4.5$
D) the constraint/s are not correct since weights are not correctly represented

Question 53

In formulating a coffee blending problem where there are three types of coffee beans, the objective is to find a recipe to make 1 pound of blended coffee that satisfies a set of properties at the least cost. The decision variables are $X_{1}, X_{2}$ , and, $X_{3}$ , representing pounds (actually fractional pounds) of coffee beans used per pound of blended coffee. Suppose that it is required to produce 200 pounds of coffee using this formulation. The appropriate constraint/s, given the definition of the problem and decision variables, will be

A) $X_{1}+X_{2}+X_{3}=200$
B) $200 X_{1}+200 X_{2}+200 X_{3}>200$
C) $200 X_{1}+200 X_{2}+200 X_{3}<200$
D) $X_{1}+X_{2}+X_{3}=1.0$ and multiply the answer by 200 to blend 200 pounds

Question 54

Wilkinson Auto Dealership sells standard automobiles and station wagons. The profit contribution for automobiles is $\$ 250.00$ per unit and that for station wagons is $\$ 500.00$ per unit. The company is planning the placement of orders with the manufacturer for next quarter. Orders for automobiles and station wagons can not exceed 320 and 160 respectively. Dealer preparation takes 2 hrs/auto and 5.00 hrs/wagon. They have 1100 hrs of preparation time next quarter. Autos take 1 unit of space, whereas wagons take 1.2 units of space. 480 units of space are available. In order to maintain some balance, the number of cars ordered should not be more than $150 \%$ the number of wagons ordered. Assume they can sell all the autos and wagons they order for the quarter. How many automobiles and wagons should be ordered in order to maximize total profit contribution? Define the decision variables, constraints, and the objective function for this problem.

Question 55

XYZ Inc. faces the following data on cost, demand and resource requirnments:

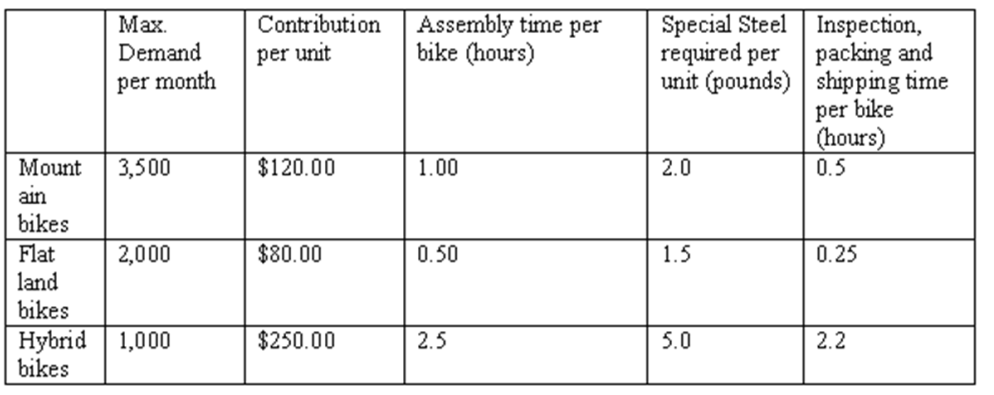
They have a total of 5,000 hours assembly time, and 9,000 hours of inspection, packing, and shipping time available per month. 4,000 pounds of special steel are available in a month. Formulate a linear programming model of this production planning problem so as to maximize the total contribution per month. Solve the problem formulated and report on the optimal solution and its corresponding objective function value.

Question 56

A company produces two products A and B. Both can be produced in any of the two machines called old machine and new machine. The following table gives the cost/unit, selling price per unit, maximum daily demand, daily variable cost budget, etc. for the products. The planning horizon is 1 day of 480 working minutes.

Each machine is available for 480 minutes a day. Daily variable cost budget is $\$ 7,200$ . As a production planner, assume that you have the freedom to decide the type and number of products to make and which machine to use, in order to maximize daily net contribution (selling price - variable cost). Formulate this as a linear program. Specify the decision variables, constraints, and the objective function. Solve it using any computer program.

Question 57

Midwest Money Manger (MMM), an investment firm, has $\$ 4$ million to invest. They have four choices, namely stocks, bonds, money-markets, and government securities. The respective projected yields are: $15 \%, 9 \%, 6 \%$ , and $4.5 \%$ . The respective risk indices are: $0.2,0.11,0.07$ , and 0.01 . It is assumed that risk index of a portfolio is equal to the weighted average value of individual index, using the proportion of investment as weights. MMM wants to limit its investment in stocks and bonds to a maximum of $50 \%$ of the total investment. Investment in money markets should always be less than or equal to investment in government securities. MMM wants to earn at least $\$ 400,000$ in the next year and minimize the risk of its portfolio. Formulate this as a linear program. Specify the decision variables, constraints, and the objective function.

Question 58

Midwest Money Manger (MMM), an investment firm, has $\$ 4$ million to invest. They have four choices, namely stocks, bonds, money-markets, and government securities. The respective projected yields are: $15 \%, 9 \%, 6 \%$ , and $4.5 \%$ . The respective risk indices are: $0.2,0.11,0.07$ , and 0.01 . It is assumed that the risk index of a portfolio is equal to the weighted average value of individual index, using the proportion of investment as weights. MMM wants to limit its investment in stocks and bonds to a maximum of $50 \%$ of the total investment. Investment in money markets should always be less than or equal to investment in government securities. MMM wants to earn at least $\$ 400,000$ in the next year and minimize the risk of its portfolio. Formulate this as a linear program. Specify the decision variables, constraints, and the objective function. Given the following formulation, verify the feasibility of the solution: Invest as follows: Stocks $=\$ 1,500,000$ ; Bonds $=\$ 750,000$ ; Money-market $=\$ 750,000$ ; Government securities $=\$ 1,000,000$ : is feasible. Is it feasible? Is it optimal?

Question 59

Midwest Money Manger (MMM), an investment firm, has $\$ 4$ million to invest. They have four choices, namely stocks, bonds, money-markets, and government securities. The respective projected yields are: $15 \%, 9 \%, 6 \%$ , and $4.5 \%$ . The respective risk indices are: $0.2,0.11,0.07$ , and 0.01 . It is assumed that the risk index of a portfolio is equal to the weighted average value of the individual index, using the proportion of investment as weights. MMM wants to limit its investment in stocks and bonds to a maximum of $50 \%$ of the total investment. Investment in money markets should always be less than or equal to investment in government securities. MMM wants its portfolio risk index to be no more than 0.105 and wants to maximize the earnings of its portfolio. Formulate this as a linear program. Specify the decision variables, constraints, and the objective function.

Question 60

Midwest Money Manger (MMM), an investment firm, has $\$ 4$ million to invest. They have four choices, namely stocks, bonds, money-markets and government securities. The respective projected yields are: $15 \%, 9 \%, 6 \%$ , and $4.5 \%$ . The respective risk indices are: $0.2,0.11,0.07$ , and 0.01 . They can also put their money in a vault (safe deposit vault), earning $0 \%$ and having a risk index of 0 . It is assumed that the risk index of a portfolio is equal to the weighted average value of the individual index, using the proportion of investment as weights. MMM wants to limit its investment in stocks and bonds to a maximum of $50 \%$ of the total investment. Investment in money markets should always be less than or equal to investment in government securities. MMM wants to earn at least $\$ 80,000$ in the next year and minimize the risk of its portfolio. Formulate this as a linear program. Specify the decision variables, constraints, and the objective function.

Question 61

A cargo plane has two compartments for storing cargo-front and back. These compartments have capacity limits on both weight and space, as summarized below.

They have three available cargo for an upcoming flight. The details of the cargo are given below.

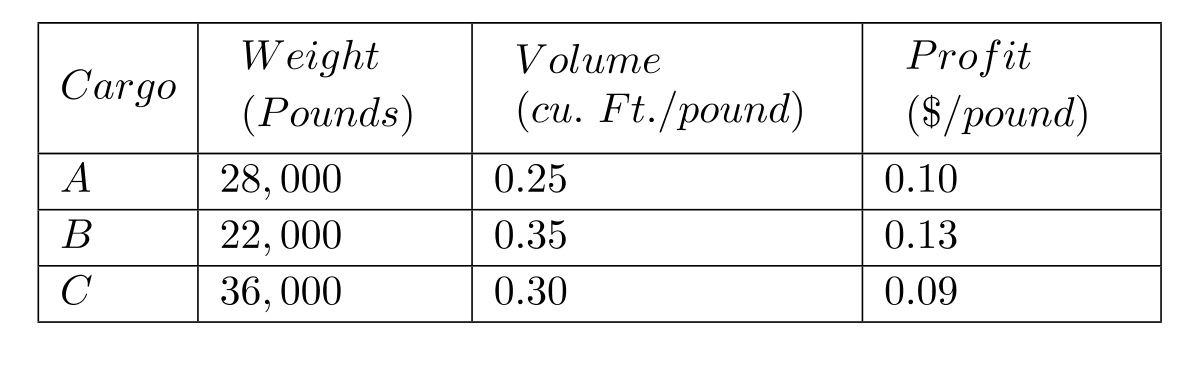
For maintaining balance, the ratio of the weight of cargo in front to the capacity of the front must be equal to the ratio of the weight of cargo at the back to the capacity of the back compartment. From each cargo, a portion of it, or the entire cargo, may be accepted. The objective is to determine how much (if any) of each of these cargo is to be accepted and how to distribute each to the front and back, so as to maximize the total profit for the flight. Formulate this as a linear program.