Exam 4: Linear Programming: Applications and Solutions

Problem A is a given formulation of a linear program with an optimal solution. Problem B is a formulation obtained by multiplying the objective function of Problem A by a negative constant and leaving all other things unchanged. Problems A and B may have

Problem $\mathrm{A}$ is a given formulation of a linear program with an optimal solution. Problem $\mathrm{B}$ is a formulation obtained from Problem A by dropping exactly one variable and leaving all other things unchanged. Problems A and B will have

In a linear programming problem with an inequality constraint and an optimal solution, if the inequality constraint is changed to an inequality constraint, all other things remaining the same, the problem may become infeasible.

In formulating a coffee blending problem where there are three types of coffee beans, the objective is to find a recipe to make 1 pound of blended coffee that satisfies a set of properties at the least cost. The decision variables are $X_{1}, X_{2}$ , and, $X_{3}$ , representing pounds (actually fractional pounds) of coffee beans used per pound of blended coffee. Suppose that it is required to produce 200 pounds of coffee using this formulation. The appropriate constraint/s, given the definition of the problem and decision variables, will be

In a typical diet problem formulation, suppose that drinking milk and eating carrots together added more nutritional value due to the interaction of the two foods in the digestive process than doing the exact same things 3 hours apart. This would still lend itself to linear programming formulation.

If a linear program does not have a feasible solution, removing one constraint from the linear program, but keeping all other things unchanged, may make the problem feasible.

A cargo plane has two compartments for storing cargo-front and back. These compartments have capacity limits on both weight and space, as summarized below. They have three available cargo for an upcoming flight. The details of the cargo are given below. 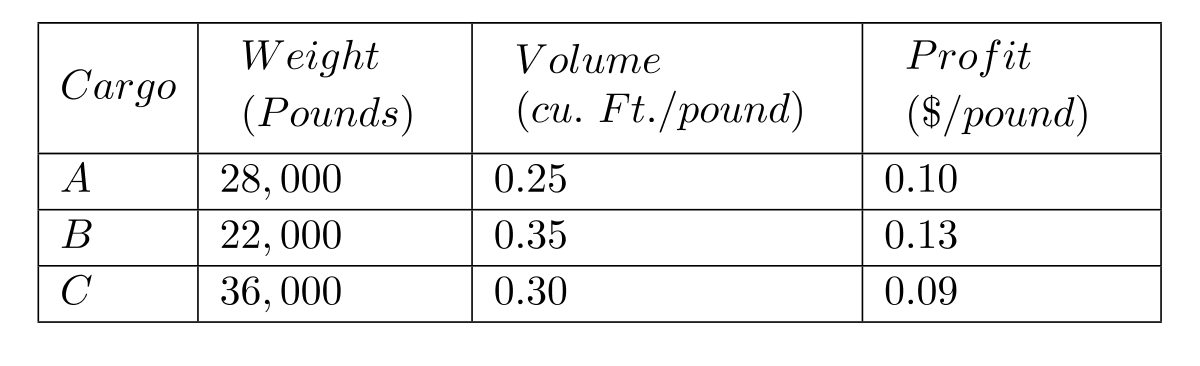For maintaining balance, the ratio of the weight of cargo in front to the capacity of the front must be equal to the ratio of the weight of cargo at the back to the capacity of the back compartment. From each cargo, a portion of it, or the entire cargo, may be accepted. The objective is to determine how much (if any) of each of these cargo is to be accepted and how to distribute each to the front and back, so as to maximize the total profit for the flight. Formulate this as a linear program.

In a linear program, if a constraint is of the form $\leq$ , solutions that make the constraint exactly equal will also be allowed.

In a linear programming problem with an equality constraint and an optimal solution, if the equality constraint is changed to an inequality constraint, all other things remaining the same, the problem may become infeasible.

In using the Solver package to solve a linear programming problem, the non-negativity constraints must be explicitly specified as part of the constraint set.

In any linear programming problem with an equality constraint, an equivalent formulation can be obtained by simply replacing the equality constraint with a pair of inequality constraints obtained by serially replacing the equality sign of the constraint with $\pounds$ and by ${ }^{3}$ signs, leaving all other things unchanged.

Problem $\mathrm{A}$ is a given formulation of a linear program with an optimal solution. Problem $\mathrm{B}$ is a formulation obtained by multiplying the objective function of Problem A by a positive constant and leaving all other things unchanged. Problems A and B will have

Problem $\mathrm{A}$ is a given formulation of a linear program with an optimal solution. Problem $\mathrm{B}$ is a formulation obtained from Problem A by omitting the non-negativity constraints and leaving all other things unchanged. Problems A and B will have

In a linear programming problem with an equality constraint and an optimal solution, if the equality constraint is changed to an inequality constraint, all other things remaining the same, the problem may become unbounded.

Problem $\mathrm{A}$ is a given formulation of a linear program with an optimal solution, and its constraint 1 is $\pounds$ type. Problem B is a formulation obtained from Problem A by replacing the $\pounds$ constraint with an equality constraint and leaving all other things unchanged. Problems A and B will have

In a typical diet problem formulation, suppose that carrots cost $\$ 1.00$ per pound if you buy one pound or less and only $\$ 0.70$ per pound if you purchase more than one pound. One of the components of the formulation is to minimize cost of the diet. This would still lend itself to linear programming formulation.

Wilkinson Auto Dealership sells standard automobiles and station wagons. The profit contribution for automobiles is $\$ 250.00$ per unit and that for station wagons is $\$ 500.00$ per unit. The company is planning the placement of orders with the manufacturer for next quarter. Orders for automobiles and station wagons can not exceed 320 and 160 respectively. Dealer preparation takes 2 hrs/auto and 5.00 hrs/wagon. They have 1100 hrs of preparation time next quarter. Autos take 1 unit of space, whereas wagons take 1.2 units of space. 480 units of space are available. In order to maintain some balance, the number of cars ordered should not be more than $150 \%$ the number of wagons ordered. Assume they can sell all the autos and wagons they order for the quarter. How many automobiles and wagons should be ordered in order to maximize total profit contribution? Define the decision variables, constraints, and the objective function for this problem.

A linear programming formulation, which has a unique optimal solution, can be infeasible for a different objective function.

In a linear program, with the decision variables corresponding to level of sales of three products, and the objective of maximizing total contribution, selling price may be used as objective function coefficients even if the net contribution per unit is given.

SUMPRODUCT command of excel can be used for multiplying elements of two arrays of unequal lengths, though it is usually used for arrays of equal length.