Deck 4: Game Theory: Games Between Three or More Players

Question 1

In a three-player game, which of the following is not one of the player designations for a payoff matrix?

A) row
B) column
C) chapter
D) page

Answer 1

chapter

Question 2

Figure 4.1 :

-Refer to Figure 4.1. Alvin is the ________ player.

A) row
B) column
C) chapter
D) page

Answer 2

page

Question 3

Figure 4.1 :

-Refer to Figure 4.1. Simon is the ________ player.

A) row
B) column
C) chapter
D) page

Answer 3

row

Question 4

Figure 4.1 :

-Refer to Figure 4.1. Theodore is the ________ player.

A) row
B) column
C) chapter
D) page

Question 5

Figure 4.1 :

-Refer to Figure 4.1. Alvin's available strategies include

A) top and bottom.
B) up and down.
C) left and right.
D) all of the above

Question 6

Figure 4.1 :

-Refer to Figure 4.1. Simon's available strategies include

A) top and bottom.
B) up and down.
C) left and right.
D) all of the above

Question 7

Figure 4.1 :

-Refer to Figure 4.1. Theodore's available strategies include

A) top and bottom.
B) up and down.
C) left and right.
D) all of the above

Question 8

Figure 4.1 :

-Refer to Figure 4.1. Suppose Alvin chooses Bottom, while Simon chooses Up, and Theodore chooses Right. Alvin's payoff will be

A) 2.
B) 6.
C) 8.
D) 16.

Question 9

Figure 4.1 :

-Refer to Figure 4.1. Suppose Alvin chooses Top, while Simon chooses Down, and Theodore chooses Right. Simon's payoff will be

A) 2.
B) 8.
C) 10.
D) 18.

Question 10

Figure 4.1 :

-Refer to Figure 4.1. Suppose Alvin chooses Top, while Simon chooses Down, and Theodore chooses Left. Theodore's payoff will be

A) 4.
B) 6.
C) 14.
D) 24.

Question 11

In a three-player game, each player must have three choices.

Question 12

When economists model a game with three players instead of two, what is different about the payoff matrix and the payoffs listed in each cell of the matrix?

Question 13

In a three-player game where each player has to make one of two choices, either North or South, how many possible choices are there, and what specifically are those choices? Identify the players as player A, player B, and player C.

Question 14

Figure 4.1 :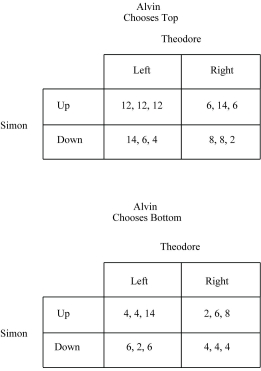

-Refer to Figure 4.1. The dominant strategy for Alvin is

A) Top.
B) Bottom.
C) both Top and Bottom.
D) Alvin does not have a dominant strategy.

Question 15

Figure 4.1 :

-Refer to Figure 4.1. The dominant strategy for Simon is

A) Up.
B) Down.
C) both Up and Down.
D) Simon does not have a dominant strategy.

Question 16

Figure 4.1 :

-Refer to Figure 4.1. The dominant strategy for Theodore is

A) Left.
B) Right.
C) both Left and Right.
D) Theodore does not have a dominant strategy.

Question 17

Figure 4.1 :

-Refer to Figure 4.1. A Nash equilibrium can be found at

A) (Up; Top; Left).
B) (Up; Top; Right).
C) (Down; Bottom; Right).
D) There is no Nash equilibrium.

Question 18

Figure 4.1 :

-Refer to Figure 4.1. The game described in the payoff matrix has the characteristics of a(n) ________ game.

A) prisoner's dilemma
B) pure coordination
C) battle of the sexes
D) assurance

Question 19

Figure 4.2:

-Refer to Figure 4.2. The dominant strategy for Ferris is to

A) go to the movie theater.
B) go to the bowling alley.
C) go to either the movie theater or to the bowling alley.
D) Ferris does not have a dominant strategy.

Question 20

Figure 4.2:

-Refer to Figure 4.2. The dominant strategy for Cameron is to

A) go to the movie theater.
B) go to the bowling alley.
C) go to either the movie theater or to the bowling alley.
D) Cameron does not have a dominant strategy.

Question 21

Figure 4.2:

-Refer to Figure 4.2. The dominant strategy for Sloane is to

A) go to the movie theater.
B) go to the bowling alley.
C) go to either the movie theater or to the bowling alley.
D) Sloane does not have a dominant strategy.

Question 22

Figure 4.2:

-Refer to Figure 4.2. Use best-response analysis to answer the following question. If Ferris's choice placed us in the movie theater, Sloane's best response, depending on the column she finds herself in, would include choosing all of the following cells except the one located at the ________ section of the appropriate payoff matrix.

A) upper right
B) upper left
C) lower right
D) lower left

Question 23

Figure 4.2:

-Refer to Figure 4.2. Use best-response analysis to answer the following question. If Ferris's choice placed us in the bowling alley, Sloane's best response, depending on the column she finds herself in, would include choosing all of the following cells except the one located at the ________ section of the appropriate payoff matrix.

A) upper right
B) upper left
C) lower right
D) lower left

Question 24

Figure 4.2:

-Refer to Figure 4.2. Use best-response analysis to answer the following question. If Ferris's choice placed us in the movie theater, Cameron's best response, depending on the row he finds himself in, would include choosing all of the following cells except the one located at the ________ section of the appropriate payoff matrix.

A) upper right
B) upper left
C) lower right
D) lower left

Question 25

Figure 4.2:

-Refer to Figure 4.2. Use best-response analysis to answer the following question. If Ferris's choice placed us in the bowling alley, Cameron's best response, depending on the row he finds himself in, would include choosing all of the following cells except the one located at the ________ section of the appropriate payoff matrix.

A) upper right
B) upper left
C) lower right
D) lower left

Question 26

Figure 4.2:

-Refer to Figure 4.2. Use best-response analysis to answer the following question. If Ferris's choice placed us in the movie theater, his best response, depending on the row and column Sloane and Cameron find themselves in, would include choosing all of the following cells except the one located at the ________ section of the appropriate payoff matrix.

A) upper right
B) upper left
C) lower right
D) lower left

Question 27

Figure 4.2:

-Refer to Figure 4.2. Use best-response analysis to answer the following question. If Ferris's choice placed us in the bowling alley, his best response, depending on the row and column Sloane and Cameron find themselves in, would include choosing all of the following cells except the one located at the ________ section of the appropriate payoff matrix.

A) upper right
B) upper left
C) lower right
D) lower left

Question 28

Figure 4.2:

-Refer to Figure 4.2. How many Nash equilibria exist in this game?

A) 0
B) 1
C) 2
D) 3

Question 29

Figure 4.2:

-Refer to Figure 4.2. A Nash equilibrium exists

A) only where all three players go to the movie theater.
B) only where all three players go to the bowling alley.
C) where all three players go to the movie theater and where all three players go to the bowling alley.
D) These is no Nash equilibrium in this game.

Question 30

Figure 4.2:

-Refer to Figure 4.2. The game described in the payoff matrix is an example of a(n) ________ game.

A) prisoner's dilemma
B) pure coordination
C) assurance
D) battle of the sexes

Question 31

In a three-player game, if a player's best choice depends on the choices made by the other two players, then the player does not have a dominant strategy.

Question 32

In a three-player game, if the game is symmetric and one player does not have a dominant strategy, then the other two players also have no dominant strategy.

Question 33

In a three-player game, a Nash equilibrium exists when all players are playing their best response to one another.

Question 34

Assume there are three players in a game, Tom, Dick, and Harry, and all three want to meet up at either at the Library or the Student Union, no player knows with certainty where the other two will go, and they will consider their mission a failure if all three do not meet at the same location. Use a series of "if-then"statements to describe Tom's ideal strategies based on the possible choices of Dick and Harry. Explain if Tom has a dominant strategy?

Question 35

Figure 4.3: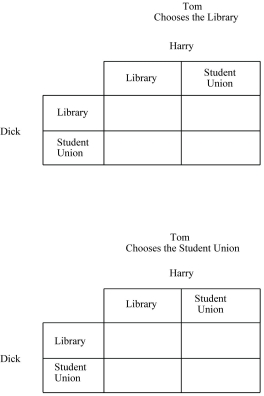
-Refer to Figure 4.3. Tom, Dick, and Harry all want to meet up at either at the Library or the Student Union, but none knows with certainty where the other two will go. They will consider their mission a success if all three meet at the same location, but will consider their mission a failure if all three do not meet at the same location. Fill in the above payoff matrix, assigning a payoff of 1 for each player when their mission is a success and a payoff of 0 for each player when their mission is a failure. Do any of the three players have a dominant strategy? If yes, identify the strategy. Are there any Nash equilibria that exist? If yes, identify them.

Question 36

In the film A Beautiful Mind, each of the three characters, Nash, Sol, and Bender, played a game where each preferred pursuing the blonde while the other two players pursued brunettes, so each preferred a different equilibrium. Also, no player had a dominant strategy in this game. Based on this, explain which of the 5 game archetypes their game did and did not represent.

Question 37

Economists often refer to games with more than three players as

A) complex games.
B) n-player games.
C) games of infinity.
D) global games.

Question 38

Games with more than three players are generally analyzed using a

A) table.
B) payoff matrix.
C) graph.
D) decision tree.

Question 39

In games with more than three players, the horizontal axis measures

A) the number of players.
B) payoffs.
C) time.
D) all of the above

Question 40

In games with more than three players, the vertical axes measure

A) the number of players.
B) payoffs.
C) time.
D) all of the above

Question 41

Figure 4.5: 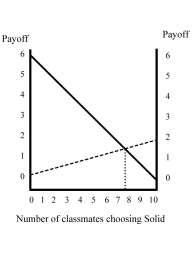You and your 9 classmates each have a chance to earn extra points on a test by selecting either the solid downsloping line or the dashed upsloping line, and the points awarded to each student will be based on the choices made by each member of the class.

-Refer to Figure 4.5. If all 10 students choose Solid, each student will earn ________ extra points.

A) 0
B) 2
C) 4
D) 6

Question 42

Figure 4.5: You and your 9 classmates each have a chance to earn extra points on a test by selecting either the solid downsloping line or the dashed upsloping line, and the points awarded to each student will be based on the choices made by each member of the class.

-Refer to Figure 4.5. If all 10 students choose Dash, each student will earn ________ extra points.

A) 0
B) 2
C) 4
D) 6

Question 43

Figure 4.5: You and your 9 classmates each have a chance to earn extra points on a test by selecting either the solid downsloping line or the dashed upsloping line, and the points awarded to each student will be based on the choices made by each member of the class.

-Refer to Figure 4.5. If you know that at least 8 students will choose Solid, you should choose

A) Solid.
B) Dash.
C) either Solid or Dash, as your payout will be the same either way.
D) You need to know what the 9th student will choose before you will know your best choice.

Question 44

Figure 4.5: You and your 9 classmates each have a chance to earn extra points on a test by selecting either the solid downsloping line or the dashed upsloping line, and the points awarded to each student will be based on the choices made by each member of the class.

-Refer to Figure 4.5. In which of the following cases will you be rewarded with the most extra points?

A) Seven of your classmates choose Dash and you and the rest choose Solid.
B) All of your other classmates choose Solid and you choose Dash.
C) Half of your classmates choose Solid and you and the rest choose Dash.
D) One of your classmates chooses Dash and you and the rest choose Solid.

Question 45

A game with more than three players is called a community game.

Question 46

In n-player games, any number of players between 4 and infinity can theoretically play.

Question 47

In a game with more than three players, the vertical axis on the left side of the graph measures payoffs and the vertical axis on the right side of the graph measures the number of players.

Question 48

What is an "n-player game"? What doe the "n"represent"?

Question 49

Explain how games with more than three players are represented graphically.

Question 50

You are at a sports memorabilia convention and you are the last of 100 people chosen to have your picture taken with either Joe Montana or Nolan Ryan. Your payoff depends on how quickly you can have your picture taken, as you have many other things you want to see at the convention. You have no preference with whom you have your picture taken, and since you were the last chosen you will be the last person in line to get your picture taken with the sports legend you select. Draw a graph that represents this 100 player game. Let the horizontal axis represent the number of people who choose to have their picture taken with Joe Montana.

Question 51

Figure 4.7: 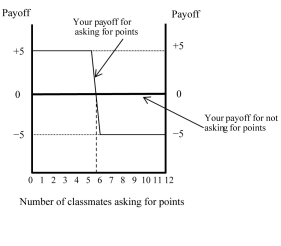Your economics professor offers you the opportunity to ask for extra points on your midterm exam. All you have to do is write "please give me points" at the bottom of the last page of the exam. Depending on the number of students who choose to ask for the extra points, either 5 points will be added to those students' grades, or 5 points will be deducted from those students' grades. If you write nothing, your grade will stay the same. There are 12 students, including you, in the class. The payoffs for this game are shown in the above figure.

-Refer to Figure 4.7. You should definitely ask for points if you believe that ________ of your classmates have asked for points.

A) five or fewer
B) less than five
C) six or more
D) more than six

Question 52

Figure 4.7: Your economics professor offers you the opportunity to ask for extra points on your midterm exam. All you have to do is write "please give me points" at the bottom of the last page of the exam. Depending on the number of students who choose to ask for the extra points, either 5 points will be added to those students' grades, or 5 points will be deducted from those students' grades. If you write nothing, your grade will stay the same. There are 12 students, including you, in the class. The payoffs for this game are shown in the above figure.

-Refer to Figure 4.7. You should definitely not ask for points if you believe that ________ of your classmates have asked for points.

A) none
B) less than five
C) five or more
D) between one and three

Question 53

Figure 4.7: Your economics professor offers you the opportunity to ask for extra points on your midterm exam. All you have to do is write "please give me points" at the bottom of the last page of the exam. Depending on the number of students who choose to ask for the extra points, either 5 points will be added to those students' grades, or 5 points will be deducted from those students' grades. If you write nothing, your grade will stay the same. There are 12 students, including you, in the class. The payoffs for this game are shown in the above figure.

-Refer to Figure 4.7. Which of the following are possible payoffs for this game?

A) 0 points
B) +5 points
C) -5 points
D) All of the above are possible payoffs.

Question 54

Figure 4.7: Your economics professor offers you the opportunity to ask for extra points on your midterm exam. All you have to do is write "please give me points" at the bottom of the last page of the exam. Depending on the number of students who choose to ask for the extra points, either 5 points will be added to those students' grades, or 5 points will be deducted from those students' grades. If you write nothing, your grade will stay the same. There are 12 students, including you, in the class. The payoffs for this game are shown in the above figure.

-Refer to Figure 4.7. You will receive a payoff of -5 points if you ask for points and so do ________ of your classmates.

A) 3
B) 4
C) 5
D) none of the above

Question 55

Figure 4.7: Your economics professor offers you the opportunity to ask for extra points on your midterm exam. All you have to do is write "please give me points" at the bottom of the last page of the exam. Depending on the number of students who choose to ask for the extra points, either 5 points will be added to those students' grades, or 5 points will be deducted from those students' grades. If you write nothing, your grade will stay the same. There are 12 students, including you, in the class. The payoffs for this game are shown in the above figure.

-Refer to Figure 4.7. You will receive a payoff of +5 points if you ask for points and so do ________ of your classmates.

A) 3
B) 5
C) 7
D) both A and B

Question 56

Figure 4.7: Your economics professor offers you the opportunity to ask for extra points on your midterm exam. All you have to do is write "please give me points" at the bottom of the last page of the exam. Depending on the number of students who choose to ask for the extra points, either 5 points will be added to those students' grades, or 5 points will be deducted from those students' grades. If you write nothing, your grade will stay the same. There are 12 students, including you, in the class. The payoffs for this game are shown in the above figure.

-Refer to Figure 4.7. You will receive a payoff of 0 points if you ask for points and so do ________ of your classmates.

A) 0
B) 6
C) 12
D) none of the above

Question 57

Figure 4.7: Your economics professor offers you the opportunity to ask for extra points on your midterm exam. All you have to do is write "please give me points" at the bottom of the last page of the exam. Depending on the number of students who choose to ask for the extra points, either 5 points will be added to those students' grades, or 5 points will be deducted from those students' grades. If you write nothing, your grade will stay the same. There are 12 students, including you, in the class. The payoffs for this game are shown in the above figure.

-Refer to Figure 4.7. An equilibrium occurs when how many students ask for points?

A) 0
B) between 5 and 6
C) 12
D) all of the above

Question 58

Figure 4.7: Your economics professor offers you the opportunity to ask for extra points on your midterm exam. All you have to do is write "please give me points" at the bottom of the last page of the exam. Depending on the number of students who choose to ask for the extra points, either 5 points will be added to those students' grades, or 5 points will be deducted from those students' grades. If you write nothing, your grade will stay the same. There are 12 students, including you, in the class. The payoffs for this game are shown in the above figure.

-Refer to Figure 4.7. The game described in the payoff graph has the characteristics of a(n) ________ game.

A) assurance
B) prisoner's dilemma
C) chicken
D) pure coordination

Question 59

Figure 4.8: You and 100 of your closest friends all decide to spend the day playing Frisbee. There are two places in town that have enough space for all of you to play Frisbee: the local beach, or the local park which is across the street from the beach. The more people who play, the more fun everyone has, and your payoff depends on the number of people that show up to the same location as you. Specifically, you will receive 5 points for each person (besides yourself) at the same location as you. Assume that everyone else's payoff is determined in the same way. The payoffs for this game are shown in the above figure.

-Refer to Figure 4.8. If half of your friends go to the beach and half go to the park, you will receive a payoff of ________ if you go to the park.

A) 0
B) 250
C) 500
D) You cannot determine the payoff from the data in the figure.

Question 60

Figure 4.8: You and 100 of your closest friends all decide to spend the day playing Frisbee. There are two places in town that have enough space for all of you to play Frisbee: the local beach, or the local park which is across the street from the beach. The more people who play, the more fun everyone has, and your payoff depends on the number of people that show up to the same location as you. Specifically, you will receive 5 points for each person (besides yourself) at the same location as you. Assume that everyone else's payoff is determined in the same way. The payoffs for this game are shown in the above figure.

-Refer to Figure 4.8. If half of your friends go to the beach and half go to the park, you will receive a payoff of ________ if you go to the beach.

A) 0
B) 250
C) 500
D) You cannot determine your payoff because the figure represents your payoff from going to the park.

Question 61

Figure 4.8: You and 100 of your closest friends all decide to spend the day playing Frisbee. There are two places in town that have enough space for all of you to play Frisbee: the local beach, or the local park which is across the street from the beach. The more people who play, the more fun everyone has, and your payoff depends on the number of people that show up to the same location as you. Specifically, you will receive 5 points for each person (besides yourself) at the same location as you. Assume that everyone else's payoff is determined in the same way. The payoffs for this game are shown in the above figure.

-Refer to Figure 4.8. If half of your friends go to the beach and half go to the park, you will receive the highest payoff by

A) going to the park.
B) going to the beach.
C) You will receive the same payoff whether you choose the beach or the park.
D) You cannot determine your highest payoff from the data in the figure.

Question 62

Figure 4.8: You and 100 of your closest friends all decide to spend the day playing Frisbee. There are two places in town that have enough space for all of you to play Frisbee: the local beach, or the local park which is across the street from the beach. The more people who play, the more fun everyone has, and your payoff depends on the number of people that show up to the same location as you. Specifically, you will receive 5 points for each person (besides yourself) at the same location as you. Assume that everyone else's payoff is determined in the same way. The payoffs for this game are shown in the above figure.

-Refer to Figure 4.8. If 30 of your friends go to the park and 70 go to the beach,

A) your friends at the beach should switch to the park.
B) your friends at the park should switch to the beach.
C) your friends at the beach should switch to the park and your friends at the park should switch to the beach.
D) your friends should stay where they are.

Question 63

Figure 4.8: You and 100 of your closest friends all decide to spend the day playing Frisbee. There are two places in town that have enough space for all of you to play Frisbee: the local beach, or the local park which is across the street from the beach. The more people who play, the more fun everyone has, and your payoff depends on the number of people that show up to the same location as you. Specifically, you will receive 5 points for each person (besides yourself) at the same location as you. Assume that everyone else's payoff is determined in the same way. The payoffs for this game are shown in the above figure.

-Refer to Figure 4.8. If half of your friends go to the beach and half go to the park, and you decide to go to the park, then

A) your friends at the beach will switch to the park.
B) you and your friends at the park will switch to the beach.
C) your friends at the beach will switch to the park and your friends at the park will switch to the beach.
D) your friends will all stay where they are.

Question 64

Figure 4.8: You and 100 of your closest friends all decide to spend the day playing Frisbee. There are two places in town that have enough space for all of you to play Frisbee: the local beach, or the local park which is across the street from the beach. The more people who play, the more fun everyone has, and your payoff depends on the number of people that show up to the same location as you. Specifically, you will receive 5 points for each person (besides yourself) at the same location as you. Assume that everyone else's payoff is determined in the same way. The payoffs for this game are shown in the above figure.

-Refer to Figure 4.8. How many different Nash equilibrium points are there in this game?

A) 0
B) 1
C) 2
D) 3

Question 65

Figure 4.8: You and 100 of your closest friends all decide to spend the day playing Frisbee. There are two places in town that have enough space for all of you to play Frisbee: the local beach, or the local park which is across the street from the beach. The more people who play, the more fun everyone has, and your payoff depends on the number of people that show up to the same location as you. Specifically, you will receive 5 points for each person (besides yourself) at the same location as you. Assume that everyone else's payoff is determined in the same way. The payoffs for this game are shown in the above figure.

-Refer to Figure 4.8. How many stable Nash equilibrium points are there in this game?

A) 0
B) 1
C) 2
D) 3

Question 66

Figure 4.8: You and 100 of your closest friends all decide to spend the day playing Frisbee. There are two places in town that have enough space for all of you to play Frisbee: the local beach, or the local park which is across the street from the beach. The more people who play, the more fun everyone has, and your payoff depends on the number of people that show up to the same location as you. Specifically, you will receive 5 points for each person (besides yourself) at the same location as you. Assume that everyone else's payoff is determined in the same way. The payoffs for this game are shown in the above figure.

-Refer to Figure 4.8. This game will end up with

A) everyone at the beach.
B) everyone at the park.
C) half of your friends at the beach and half at the park.
D) either a or b

Question 67

Figure 4.8: You and 100 of your closest friends all decide to spend the day playing Frisbee. There are two places in town that have enough space for all of you to play Frisbee: the local beach, or the local park which is across the street from the beach. The more people who play, the more fun everyone has, and your payoff depends on the number of people that show up to the same location as you. Specifically, you will receive 5 points for each person (besides yourself) at the same location as you. Assume that everyone else's payoff is determined in the same way. The payoffs for this game are shown in the above figure.

-Refer to Figure 4.8. The game described in the payoff graph has the characteristics of a(n) ________ game.

A) assurance
B) prisoner's dilemma
C) chicken
D) pure coordination

Question 68

Assume there are two competing social network sites, Mugshot and Graybar, and each grow in value as more people use them. Mugshot has been around longer and has the most users, but people tend to agree that Graybar is a better site, so the equilibrium where everyone uses Graybar is preferred to the equilibrium where everyone uses Mugshot. This situation describes a multiplayer

A) assurance game.
B) prisoner's dilemma game.
C) battle of the sexes game.
D) pure coordination game.

Question 69

In a multiplayer game of chicken, there can be no Nash equilibrium.

Question 70

In a multiplayer game of chicken, natural incentives tend to push the outcome toward the point where payoffs to the two strategies are identical.

Question 71

In a multiplayer game where there are two equally-enjoyable choices of what to do, and everyone wants to do what everyone else is doing, there will be three Nash equilibria.

Question 72

In a multiplayer game where there are two equally-enjoyable choices of what to do, and everyone wants to do what everyone else is doing, only one Nash equilibrium is stable.

Question 73

Figure 4.9: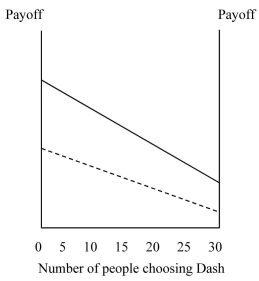
-Refer to Figure 4.9. Payoffs for playing Solid and Dash are indicated by the appropriate lines in the figure.Answer the following questions based on the above figure:
a. If you were playing this game, what would you choose if you thought everyone was playing Solid?
b. If you were playing this game, what would you choose if you thought everyone was playing Dash?
c. What is the dominant strategy in this game?
d. What is the equilibrium outcome in this game?

Question 74

You are at a sports memorabilia convention and you are the last of 100 people chosen to have your picture taken with either Joe Montana or Nolan Ryan. Your payoff depends on how quickly you can have your picture taken, as you have many other things you want to see at the convention. You have no preference with whom you have your picture taken, and since you were the last chosen you will be the last person in line to get your picture taken with the sports legend you select. Identify all the Nash equilibria in this game and explain your reasoning.