Exam 4: Game Theory: Games Between Three or More Players
Exam 1: Fundamental Concepts in Economics100 Questions
Exam 2: Cost-Benefit Analysis and the Value of a Life73 Questions
Exam 3: Basic Game Theory: Games Between Two Players71 Questions
Exam 4: Game Theory: Games Between Three or More Players74 Questions
Exam 5: Free Exchange: Individual and International Trade67 Questions
Exam 6: The Market System: Functions, Structure, and Institutions69 Questions
Exam 7: The Nature of Pollution Problems61 Questions
Exam 8: Government Policies to Regulate Pollution49 Questions
Exam 9: Resource Depletion and Sustainability65 Questions
Exam 10: Public Goods and the Role of Government59 Questions
Exam 11: Public Goods: Tackling Large Projects and Eminent Domain68 Questions
Exam 12: The Volunteers Dilemma: a Collective Inaction Problem75 Questions
Exam 13: Voting: You Cant Always Get What You Want69 Questions
Exam 14: The Economics of Health Insurance and Health Care66 Questions
Exam 15: Segregation and Discrimination69 Questions
Exam 16: Gross Domestic Product and the Wealth of Nations: an Introduction to the Macroeconomy59 Questions
Exam 17: Unemployment66 Questions
Exam 18: An Introduction to Money, Banks, and the Financial System57 Questions
Exam 19: The Federal Reserve: Monetary Policy, Economic Activity, and Inflation65 Questions
Exam 20: The Federal Government: Taxes, Spending, and Fiscal Policy66 Questions
Exam 21: Income Inequality and the Redistribution of Income69 Questions
Select questions type
In a multiplayer game of chicken, there can be no Nash equilibrium.
Free
(True/False)
4.9/5  (36)
(36)
Correct Answer:
False
In a game with more than three players, the vertical axis on the left side of the graph measures payoffs and the vertical axis on the right side of the graph measures the number of players.
Free
(True/False)
4.8/5  (33)
(33)
Correct Answer:
False
In games with more than three players, the vertical axes measure
Free
(Multiple Choice)
4.7/5  (32)
(32)
Correct Answer:
B
In a multiplayer game where there are two equally-enjoyable choices of what to do, and everyone wants to do what everyone else is doing, only one Nash equilibrium is stable.
(True/False)
4.9/5  (34)
(34)
Figure 4.5: 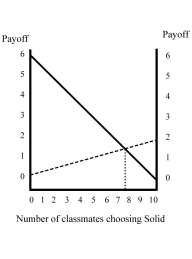 You and your 9 classmates each have a chance to earn extra points on a test by selecting either the solid downsloping line or the dashed upsloping line, and the points awarded to each student will be based on the choices made by each member of the class.
-Refer to Figure 4.5. If all 10 students choose Dash, each student will earn ________ extra points.
You and your 9 classmates each have a chance to earn extra points on a test by selecting either the solid downsloping line or the dashed upsloping line, and the points awarded to each student will be based on the choices made by each member of the class.
-Refer to Figure 4.5. If all 10 students choose Dash, each student will earn ________ extra points.
(Multiple Choice)
4.7/5  (33)
(33)
Figure 4.5:  You and your 9 classmates each have a chance to earn extra points on a test by selecting either the solid downsloping line or the dashed upsloping line, and the points awarded to each student will be based on the choices made by each member of the class.
-Refer to Figure 4.5. If you know that at least 8 students will choose Solid, you should choose
You and your 9 classmates each have a chance to earn extra points on a test by selecting either the solid downsloping line or the dashed upsloping line, and the points awarded to each student will be based on the choices made by each member of the class.
-Refer to Figure 4.5. If you know that at least 8 students will choose Solid, you should choose
(Multiple Choice)
4.8/5  (42)
(42)
Figure 4.7: 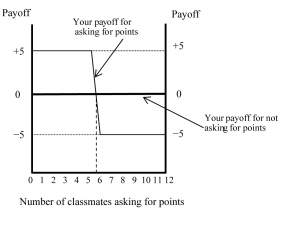 Your economics professor offers you the opportunity to ask for extra points on your midterm exam. All you have to do is write "please give me points" at the bottom of the last page of the exam. Depending on the number of students who choose to ask for the extra points, either 5 points will be added to those students' grades, or 5 points will be deducted from those students' grades. If you write nothing, your grade will stay the same. There are 12 students, including you, in the class. The payoffs for this game are shown in the above figure.
-Refer to Figure 4.7. You should definitely not ask for points if you believe that ________ of your classmates have asked for points.
Your economics professor offers you the opportunity to ask for extra points on your midterm exam. All you have to do is write "please give me points" at the bottom of the last page of the exam. Depending on the number of students who choose to ask for the extra points, either 5 points will be added to those students' grades, or 5 points will be deducted from those students' grades. If you write nothing, your grade will stay the same. There are 12 students, including you, in the class. The payoffs for this game are shown in the above figure.
-Refer to Figure 4.7. You should definitely not ask for points if you believe that ________ of your classmates have asked for points.
(Multiple Choice)
4.8/5  (40)
(40)
Explain how games with more than three players are represented graphically.
(Essay)
4.8/5  (35)
(35)
Figure 4.8: 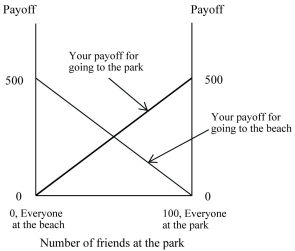 You and 100 of your closest friends all decide to spend the day playing Frisbee. There are two places in town that have enough space for all of you to play Frisbee: the local beach, or the local park which is across the street from the beach. The more people who play, the more fun everyone has, and your payoff depends on the number of people that show up to the same location as you. Specifically, you will receive 5 points for each person (besides yourself) at the same location as you. Assume that everyone else's payoff is determined in the same way. The payoffs for this game are shown in the above figure.
-Refer to Figure 4.8. This game will end up with
You and 100 of your closest friends all decide to spend the day playing Frisbee. There are two places in town that have enough space for all of you to play Frisbee: the local beach, or the local park which is across the street from the beach. The more people who play, the more fun everyone has, and your payoff depends on the number of people that show up to the same location as you. Specifically, you will receive 5 points for each person (besides yourself) at the same location as you. Assume that everyone else's payoff is determined in the same way. The payoffs for this game are shown in the above figure.
-Refer to Figure 4.8. This game will end up with
(Multiple Choice)
4.8/5  (29)
(29)
Figure 4.5:  You and your 9 classmates each have a chance to earn extra points on a test by selecting either the solid downsloping line or the dashed upsloping line, and the points awarded to each student will be based on the choices made by each member of the class.
-Refer to Figure 4.5. If all 10 students choose Solid, each student will earn ________ extra points.
You and your 9 classmates each have a chance to earn extra points on a test by selecting either the solid downsloping line or the dashed upsloping line, and the points awarded to each student will be based on the choices made by each member of the class.
-Refer to Figure 4.5. If all 10 students choose Solid, each student will earn ________ extra points.
(Multiple Choice)
4.7/5  (25)
(25)
Games with more than three players are generally analyzed using a
(Multiple Choice)
4.9/5  (38)
(38)
Figure 4.1 : 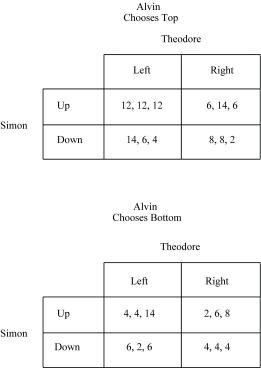 -Refer to Figure 4.1. Suppose Alvin chooses Top, while Simon chooses Down, and Theodore chooses Left. Theodore's payoff will be
-Refer to Figure 4.1. Suppose Alvin chooses Top, while Simon chooses Down, and Theodore chooses Left. Theodore's payoff will be
(Multiple Choice)
4.9/5  (34)
(34)
Figure 4.7:  Your economics professor offers you the opportunity to ask for extra points on your midterm exam. All you have to do is write "please give me points" at the bottom of the last page of the exam. Depending on the number of students who choose to ask for the extra points, either 5 points will be added to those students' grades, or 5 points will be deducted from those students' grades. If you write nothing, your grade will stay the same. There are 12 students, including you, in the class. The payoffs for this game are shown in the above figure.
-Refer to Figure 4.7. You should definitely ask for points if you believe that ________ of your classmates have asked for points.
Your economics professor offers you the opportunity to ask for extra points on your midterm exam. All you have to do is write "please give me points" at the bottom of the last page of the exam. Depending on the number of students who choose to ask for the extra points, either 5 points will be added to those students' grades, or 5 points will be deducted from those students' grades. If you write nothing, your grade will stay the same. There are 12 students, including you, in the class. The payoffs for this game are shown in the above figure.
-Refer to Figure 4.7. You should definitely ask for points if you believe that ________ of your classmates have asked for points.
(Multiple Choice)
4.9/5  (30)
(30)
In a three-player game, a Nash equilibrium exists when all players are playing their best response to one another.
(True/False)
4.8/5  (36)
(36)
Figure 4.2: 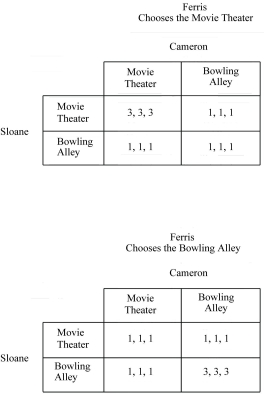 -Refer to Figure 4.2. The dominant strategy for Sloane is to
-Refer to Figure 4.2. The dominant strategy for Sloane is to
(Multiple Choice)
4.7/5  (39)
(39)
Figure 4.2:  -Refer to Figure 4.2. A Nash equilibrium exists
-Refer to Figure 4.2. A Nash equilibrium exists
(Multiple Choice)
4.8/5  (37)
(37)
Figure 4.7:  Your economics professor offers you the opportunity to ask for extra points on your midterm exam. All you have to do is write "please give me points" at the bottom of the last page of the exam. Depending on the number of students who choose to ask for the extra points, either 5 points will be added to those students' grades, or 5 points will be deducted from those students' grades. If you write nothing, your grade will stay the same. There are 12 students, including you, in the class. The payoffs for this game are shown in the above figure.
-Refer to Figure 4.7. You will receive a payoff of +5 points if you ask for points and so do ________ of your classmates.
Your economics professor offers you the opportunity to ask for extra points on your midterm exam. All you have to do is write "please give me points" at the bottom of the last page of the exam. Depending on the number of students who choose to ask for the extra points, either 5 points will be added to those students' grades, or 5 points will be deducted from those students' grades. If you write nothing, your grade will stay the same. There are 12 students, including you, in the class. The payoffs for this game are shown in the above figure.
-Refer to Figure 4.7. You will receive a payoff of +5 points if you ask for points and so do ________ of your classmates.
(Multiple Choice)
4.8/5  (34)
(34)
Figure 4.8:  You and 100 of your closest friends all decide to spend the day playing Frisbee. There are two places in town that have enough space for all of you to play Frisbee: the local beach, or the local park which is across the street from the beach. The more people who play, the more fun everyone has, and your payoff depends on the number of people that show up to the same location as you. Specifically, you will receive 5 points for each person (besides yourself) at the same location as you. Assume that everyone else's payoff is determined in the same way. The payoffs for this game are shown in the above figure.
-Refer to Figure 4.8. If 30 of your friends go to the park and 70 go to the beach,
You and 100 of your closest friends all decide to spend the day playing Frisbee. There are two places in town that have enough space for all of you to play Frisbee: the local beach, or the local park which is across the street from the beach. The more people who play, the more fun everyone has, and your payoff depends on the number of people that show up to the same location as you. Specifically, you will receive 5 points for each person (besides yourself) at the same location as you. Assume that everyone else's payoff is determined in the same way. The payoffs for this game are shown in the above figure.
-Refer to Figure 4.8. If 30 of your friends go to the park and 70 go to the beach,
(Multiple Choice)
4.8/5  (37)
(37)
You are at a sports memorabilia convention and you are the last of 100 people chosen to have your picture taken with either Joe Montana or Nolan Ryan. Your payoff depends on how quickly you can have your picture taken, as you have many other things you want to see at the convention. You have no preference with whom you have your picture taken, and since you were the last chosen you will be the last person in line to get your picture taken with the sports legend you select. Identify all the Nash equilibria in this game and explain your reasoning.
(Essay)
4.8/5  (34)
(34)
Figure 4.9: 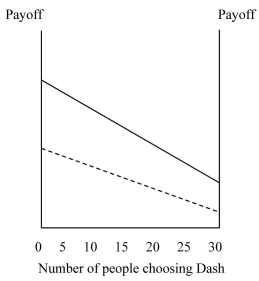 -Refer to Figure 4.9. Payoffs for playing Solid and Dash are indicated by the appropriate lines in the figure.Answer the following questions based on the above figure:
a. If you were playing this game, what would you choose if you thought everyone was playing Solid?
b. If you were playing this game, what would you choose if you thought everyone was playing Dash?
c. What is the dominant strategy in this game?
d. What is the equilibrium outcome in this game?
-Refer to Figure 4.9. Payoffs for playing Solid and Dash are indicated by the appropriate lines in the figure.Answer the following questions based on the above figure:
a. If you were playing this game, what would you choose if you thought everyone was playing Solid?
b. If you were playing this game, what would you choose if you thought everyone was playing Dash?
c. What is the dominant strategy in this game?
d. What is the equilibrium outcome in this game?
(Short Answer)
4.9/5  (34)
(34)
Showing 1 - 20 of 74
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)