Deck 4: Applications of the Derivative
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/228
Play
Full screen (f)
Deck 4: Applications of the Derivative
1
Determine all critical points for the function.
-f(x) =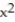 + 6x + 9
+ 6x + 9
A) x = 3
B) x = 0
C) x = -6
D) x = -3
-f(x) =
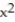 + 6x + 9
+ 6x + 9A) x = 3
B) x = 0
C) x = -6
D) x = -3
x = -3
2
Determine all critical points for the function.
-f(x) =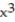 - 12x - 5
- 12x - 5
A) x = -2
B) x = -2 and x = 2
C) x = 2
D) x = -2, x = 0, and x = 2
-f(x) =
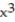 - 12x - 5
- 12x - 5A) x = -2
B) x = -2 and x = 2
C) x = 2
D) x = -2, x = 0, and x = 2
x = -2 and x = 2
3
Determine all critical points for the function.
-f(x) =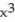 - 9
- 9 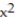 + 10
+ 10
A) x = 0 and x = 6
B) x = -3 and x = 3
C) x = 0
D) x = 0 and x = 3
-f(x) =
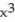 - 9
- 9 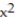 + 10
+ 10A) x = 0 and x = 6
B) x = -3 and x = 3
C) x = 0
D) x = 0 and x = 3
x = 0 and x = 6
4
Determine all critical points for the function.
-f(x) = 5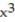 - 3
- 3 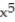
A) x = -1 and x = 1
B) x = -1
C) x = 0, x = -1, and x = 1
D) x = 1
-f(x) = 5
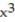 - 3
- 3 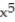
A) x = -1 and x = 1
B) x = -1
C) x = 0, x = -1, and x = 1
D) x = 1

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
5
Determine all critical points for the function.
-f(x) =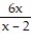
A) x = -12 and x = 0
B) x = 2
C) x = -2
D) x = 0 and x = 2
-f(x) =
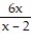
A) x = -12 and x = 0
B) x = 2
C) x = -2
D) x = 0 and x = 2

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
6
Determine all critical points for the function.
-f(x) =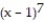
A) x = 0 and x = 1
B) x = 1
C) x = 1 and x = 7
D) x = 0, x = 1, and x = 7
-f(x) =
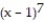
A) x = 0 and x = 1
B) x = 1
C) x = 1 and x = 7
D) x = 0, x = 1, and x = 7

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
7
Determine all critical points for the function.
-y = 3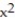 - 96
- 96 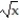
A) x = 4
B) x = 0 and x = 4
C) x = 0, x = 4, and x = -4
D) x = 0
-y = 3
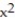 - 96
- 96 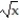
A) x = 4
B) x = 0 and x = 4
C) x = 0, x = 4, and x = -4
D) x = 0

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
8
Find the absolute extreme values of the function on the interval.
-g(x) = -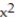 + 5x - 6, 2 x 3
+ 5x - 6, 2 x 3
A) absolute maximum is 1/4 at x = 7/2; absolute minimum is 0 at 3 and 0 at x = 2
B) absolute maximum is 5/4 at x = 7/2; absolute minimum is 0 at 3 and 0 at x = 2
C) absolute maximum is 49/4 at x = 5/2; absolute minimum is 0 at 3 and 0 at x = 2
D) absolute maximum is 1/4 at x = 5/2; absolute minimum is 0 at 3 and 0 at x = 2
-g(x) = -
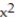 + 5x - 6, 2 x 3
+ 5x - 6, 2 x 3A) absolute maximum is 1/4 at x = 7/2; absolute minimum is 0 at 3 and 0 at x = 2
B) absolute maximum is 5/4 at x = 7/2; absolute minimum is 0 at 3 and 0 at x = 2
C) absolute maximum is 49/4 at x = 5/2; absolute minimum is 0 at 3 and 0 at x = 2
D) absolute maximum is 1/4 at x = 5/2; absolute minimum is 0 at 3 and 0 at x = 2

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
9
Find the absolute extreme values of the function on the interval.
-f( ) = sin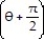 , 0
, 0 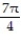
A) absolute maximum is 1 at = 0; absolute minimum is -1 at =
B) absolute maximum is 1 at = 7/8 ; absolute minimum is -1 at = 1/8 ,
C) absolute maximum is 1 at = 9/8 ; absolute minimum is -1 at = 7/8
D) absolute maximum is 1 at = 1/8 ; absolute minimum is -1 at = 7/8 ,
-f( ) = sin
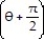 , 0
, 0 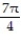
A) absolute maximum is 1 at = 0; absolute minimum is -1 at =
B) absolute maximum is 1 at = 7/8 ; absolute minimum is -1 at = 1/8 ,
C) absolute maximum is 1 at = 9/8 ; absolute minimum is -1 at = 7/8
D) absolute maximum is 1 at = 1/8 ; absolute minimum is -1 at = 7/8 ,

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
10
Find the absolute extreme values of the function on the interval.
-f(x) = csc x, -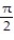 x
x 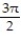
A) absolute maximum is 1 at x = ; absolute minimum is -1 at x =
B) absolute maximum does not exist; absolute minimum does not exist
C) absolute maximum is 0 at x = - ; absolute minimum is -1 at x =
D) absolute maximum is -1 at x = ; absolute minimum is 1 at x = 0
-f(x) = csc x, -
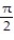 x
x 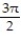
A) absolute maximum is 1 at x = ; absolute minimum is -1 at x =
B) absolute maximum does not exist; absolute minimum does not exist
C) absolute maximum is 0 at x = - ; absolute minimum is -1 at x =
D) absolute maximum is -1 at x = ; absolute minimum is 1 at x = 0

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
11
Find the absolute extreme values of the function on the interval.
-F(x) = -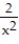 , 0.5 x 2
, 0.5 x 2
A) absolute maximum is 1/2 at x = 1/ 2; absolute minimum is -8 at x = 2
B) absolute maximum is - 1/2 at x = 2 ; absolute minimum is -8 at x = 1/2
C) absolute maximum is - 1/2 at x = 1/ 2; absolute minimum is -8 at x = - 2
D) absolute maximum is at x = -1/2 at x = 2 ; absolute minimum is -8 at x = -1/2
-F(x) = -
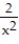 , 0.5 x 2
, 0.5 x 2A) absolute maximum is 1/2 at x = 1/ 2; absolute minimum is -8 at x = 2
B) absolute maximum is - 1/2 at x = 2 ; absolute minimum is -8 at x = 1/2
C) absolute maximum is - 1/2 at x = 1/ 2; absolute minimum is -8 at x = - 2
D) absolute maximum is at x = -1/2 at x = 2 ; absolute minimum is -8 at x = -1/2

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
12
Find the absolute extreme values of the function on the interval.
-F(x) =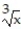 , -1 x 27
, -1 x 27
A) absolute maximum is 3 at x = 27; absolute minimum is 0 at x =0
B) absolute maximum is 3 at x = 27; absolute minimum is -3 at x = -27
C) absolute maximum is 0 at x = 0; absolute minimum is 3 at x = 27
D) absolute maximum is 3 at x = -27; absolute minimum is 0 at x =0
-F(x) =
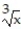 , -1 x 27
, -1 x 27A) absolute maximum is 3 at x = 27; absolute minimum is 0 at x =0
B) absolute maximum is 3 at x = 27; absolute minimum is -3 at x = -27
C) absolute maximum is 0 at x = 0; absolute minimum is 3 at x = 27
D) absolute maximum is 3 at x = -27; absolute minimum is 0 at x =0

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
13
Find the absolute extreme values of the function on the interval.
-h(x) =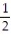 x + 5, -2 x 3
x + 5, -2 x 3
A) absolute maximum is - 7/2 at x = -2; absolute minimum is 4 at x = 3
B) absolute maximum is 13/2 at x = 3; absolute minimum is 4 at x = -2
C) absolute maximum is - 7/2 at x = -3; absolute minimum is -3 at x = 2
D) absolute maximum is - 7/2 at x = 3; absolute minimum is 4 at x = -2
-h(x) =
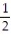 x + 5, -2 x 3
x + 5, -2 x 3A) absolute maximum is - 7/2 at x = -2; absolute minimum is 4 at x = 3
B) absolute maximum is 13/2 at x = 3; absolute minimum is 4 at x = -2
C) absolute maximum is - 7/2 at x = -3; absolute minimum is -3 at x = 2
D) absolute maximum is - 7/2 at x = 3; absolute minimum is 4 at x = -2

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
14
Find the absolute extreme values of the function on the interval.
-g(x) = 7 - 6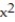 , -2 x 3
, -2 x 3
A) absolute maximum is 14 at x = 0; absolute minimum is -17 at x = 3
B) absolute maximum is 7 at x = 0; absolute minimum is -47 at x = 3
C) absolute maximum is 6 at x = 0; absolute minimum is -61 at x = 3
D) absolute maximum is 42 at x = 0; absolute minimum is -17 at x = -2
-g(x) = 7 - 6
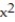 , -2 x 3
, -2 x 3A) absolute maximum is 14 at x = 0; absolute minimum is -17 at x = 3
B) absolute maximum is 7 at x = 0; absolute minimum is -47 at x = 3
C) absolute maximum is 6 at x = 0; absolute minimum is -61 at x = 3
D) absolute maximum is 42 at x = 0; absolute minimum is -17 at x = -2

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
15
Find the absolute extreme values of the function on the interval.
-f(x) = tan x, -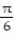 x
x 
A)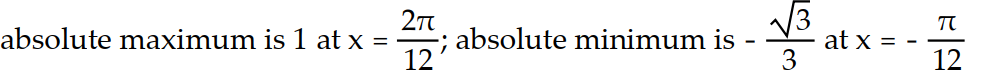
B)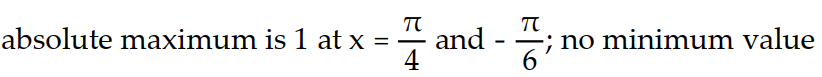
C)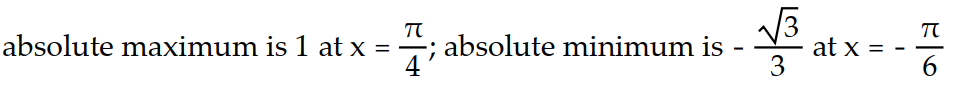
D)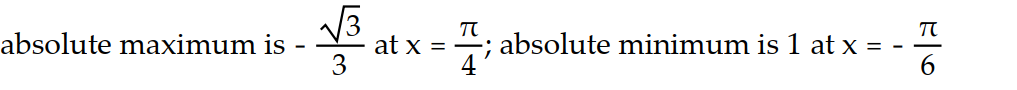
-f(x) = tan x, -
 x
x 
A)
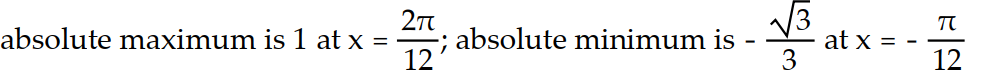
B)
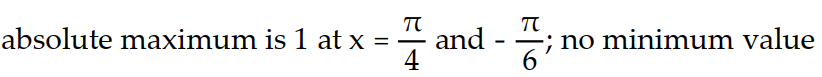
C)
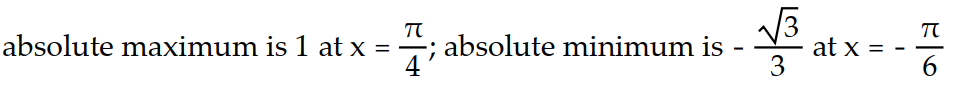
D)
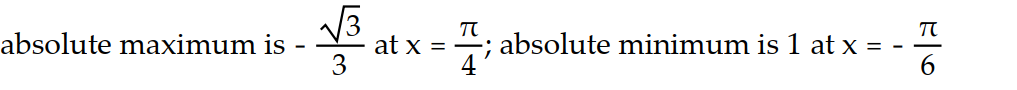

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
16
Find the absolute extreme values of the function on the interval.
-f(x) =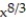 , -1 x 8
, -1 x 8
A) absolute maximum is 512 at x = 8; absolute minimum is 0 at x = 01
B) absolute maximum is 256 at x = 8; absolute minimum is 1 at x = -1
C)absolute maximum is 256 at x = 8; absolute minimum does not exist
D) absolute maximum is 256 at x = 8; absolute minimum is 0 at x = 01
-f(x) =
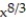 , -1 x 8
, -1 x 8A) absolute maximum is 512 at x = 8; absolute minimum is 0 at x = 01
B) absolute maximum is 256 at x = 8; absolute minimum is 1 at x = -1
C)absolute maximum is 256 at x = 8; absolute minimum does not exist
D) absolute maximum is 256 at x = 8; absolute minimum is 0 at x = 01

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
17
Find the absolute extreme values of the function on the interval.
-f(x) = 7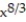 , -27 x 8
, -27 x 8
A) absolute maximum is 1792 at x = 8 ; absolute minimum is 0 at x = 0
B) absolute maximum is 6561 at x = -27 ; absolute minimum is 0 at x = 0
C) absolute maximum is 45,927 at x = -27 ; absolute minimum is 0 at x = 0
D) absolute maximum is 45,927 at x = -27 ; absolute minimum is 1792 at x = 8
-f(x) = 7
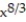 , -27 x 8
, -27 x 8A) absolute maximum is 1792 at x = 8 ; absolute minimum is 0 at x = 0
B) absolute maximum is 6561 at x = -27 ; absolute minimum is 0 at x = 0
C) absolute maximum is 45,927 at x = -27 ; absolute minimum is 0 at x = 0
D) absolute maximum is 45,927 at x = -27 ; absolute minimum is 1792 at x = 8

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
18
Find the absolute extreme values of the function on the interval.
-f(x) = ln(x + 2) + , 1 x 5
, 1 x 5
A) absolute minimum value is ln 4 + 1/2 at x = 2; absolute maximum value is ln 3 + 1 at x = 1
B) absolute minimum value is ln 4 + 1/2 at x = 2; absolute maximum value is ln 7 + 1/5 at x = 5
C) absolute minimum value is ln 3 + 1 at x = 1; absolute maximum value is ln 7 + 1/5 at x = 5
D) absolute minimum value is -1 at x = -1; absolute maximum value is ln 7 + 1/5 at x = 5
-f(x) = ln(x + 2) +
 , 1 x 5
, 1 x 5A) absolute minimum value is ln 4 + 1/2 at x = 2; absolute maximum value is ln 3 + 1 at x = 1
B) absolute minimum value is ln 4 + 1/2 at x = 2; absolute maximum value is ln 7 + 1/5 at x = 5
C) absolute minimum value is ln 3 + 1 at x = 1; absolute maximum value is ln 7 + 1/5 at x = 5
D) absolute minimum value is -1 at x = -1; absolute maximum value is ln 7 + 1/5 at x = 5

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
19
Find the absolute extreme values of the function on the interval.
-f(x) = - 6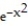 , - < x <
, - < x <
A) no minimum value and no maximum value
B) absolute maximum value is - 6 at x = 0; no minimum value
C) absolute minimum value is - 6 at x = 0; no maximum value
D) absolute minimum value is - 6 at x = 0; absolute maximum value is - 6/e at x = 1
-f(x) = - 6
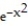 , - < x <
, - < x < A) no minimum value and no maximum value
B) absolute maximum value is - 6 at x = 0; no minimum value
C) absolute minimum value is - 6 at x = 0; no maximum value
D) absolute minimum value is - 6 at x = 0; absolute maximum value is - 6/e at x = 1

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
20
Find the absolute extreme values of the function on the interval.
-f(x) = ln (-x), -6 x -1
A) absolute maximum value is 0 at x = -1; absolute minimum value is -ln 6 at x = -6
B) absolute minimum value is 0 at x = -1; no maximum value
C) no minimum value; no maximum value
D) absolute minimum value is 0 at x = -1; absolute maximum value is ln 6 at x = -6
-f(x) = ln (-x), -6 x -1
A) absolute maximum value is 0 at x = -1; absolute minimum value is -ln 6 at x = -6
B) absolute minimum value is 0 at x = -1; no maximum value
C) no minimum value; no maximum value
D) absolute minimum value is 0 at x = -1; absolute maximum value is ln 6 at x = -6

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
21
Find the absolute extreme values of the function on the interval.
-f(x) =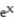 - x, -4 x 2
- x, -4 x 2
A) absolute minimum value is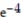 + 4 at x = -4; absolute maximum value is
+ 4 at x = -4; absolute maximum value is 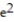 - 2 at x = 2
- 2 at x = 2
B) absolute minimum value is 1 at x = 0; absolute maximum value is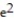 - 2 at x = 2
- 2 at x = 2
C) absolute minimum value is 1 at x = 0; absolute maximum value is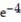 + 4 at x = -4
+ 4 at x = -4
D) absolute minimum value is 1 at x = 0; no maximum value
-f(x) =
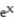 - x, -4 x 2
- x, -4 x 2A) absolute minimum value is
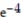 + 4 at x = -4; absolute maximum value is
+ 4 at x = -4; absolute maximum value is 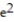 - 2 at x = 2
- 2 at x = 2B) absolute minimum value is 1 at x = 0; absolute maximum value is
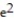 - 2 at x = 2
- 2 at x = 2C) absolute minimum value is 1 at x = 0; absolute maximum value is
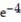 + 4 at x = -4
+ 4 at x = -4D) absolute minimum value is 1 at x = 0; no maximum value

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
22
Find the extreme values of the function and where they occur.
-y = x2 + 2x - 3
A) Absolute minimum is 1 at x = 4.
B) Absolute minimum is -4 at x = -1.
C) Absolute minimum is -1 at x = 4.
D) Absolute minimum is 1 at x = -4.
-y = x2 + 2x - 3
A) Absolute minimum is 1 at x = 4.
B) Absolute minimum is -4 at x = -1.
C) Absolute minimum is -1 at x = 4.
D) Absolute minimum is 1 at x = -4.

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
23
Find the extreme values of the function and where they occur.
-y = x3 - 3x2 + 1
A) Local maximum at (0, 1), local minimum at (2, -3).
B) Local minimum at (2, -3).
C) None
D) Local maximum at (0, 1).
-y = x3 - 3x2 + 1
A) Local maximum at (0, 1), local minimum at (2, -3).
B) Local minimum at (2, -3).
C) None
D) Local maximum at (0, 1).

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
24
Find the extreme values of the function and where they occur.
-y = x3 - 12x + 2
A) Local maximum at (0, 0).
B) None
C) Local maximum at (-2, 18), local minimum at (2, -14).
D) Local maximum at (2, -14), local minimum at (-2, 18).
-y = x3 - 12x + 2
A) Local maximum at (0, 0).
B) None
C) Local maximum at (-2, 18), local minimum at (2, -14).
D) Local maximum at (2, -14), local minimum at (-2, 18).

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
25
Find the extreme values of the function and where they occur.
-y =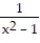
A) None
B) Local maximum at (1, 0), local minimum at (-1, 0).
C) Local maximum at (0, -1).
D) Local maximum at (-1, 0), local minimum at (1,0).
-y =
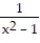
A) None
B) Local maximum at (1, 0), local minimum at (-1, 0).
C) Local maximum at (0, -1).
D) Local maximum at (-1, 0), local minimum at (1,0).

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
26
Find the extreme values of the function and where they occur.
-y =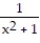
A) Absolute maximum value is 1 at x = 0.5, absolute minimum value is -1 at x = 0.5.
B) Absolute maximum value is 1 at x = 0.
C) Absolute maximum value is 1 at x = 0.5.
D) Absolute minimum value is -1 at x = 0.5.
-y =
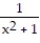
A) Absolute maximum value is 1 at x = 0.5, absolute minimum value is -1 at x = 0.5.
B) Absolute maximum value is 1 at x = 0.
C) Absolute maximum value is 1 at x = 0.5.
D) Absolute minimum value is -1 at x = 0.5.

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
27
Find the extreme values of the function and where they occur.
-y =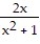
A) Absolute maximum value is 0 at x = 0.
B) Absolute minimum value is 0 at x = 1. Absolute maximum value is 0 at x = -1.
C) Absolute minimum value is - 1 at x = -1. Absolute maximum value is 1at x = 1.
D) Absolute minimum value is 0 at x = 0.
-y =
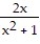
A) Absolute maximum value is 0 at x = 0.
B) Absolute minimum value is 0 at x = 1. Absolute maximum value is 0 at x = -1.
C) Absolute minimum value is - 1 at x = -1. Absolute maximum value is 1at x = 1.
D) Absolute minimum value is 0 at x = 0.

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
28
Find the extreme values of the function and where they occur.
-y =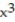 - 3
- 3 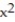 + 6x - 8
+ 6x - 8
A) None
B) Absolute minimum is 4 at x = -1.
C) Absolute maximum is 4 at x = 2.
D) Absolute maximum is 4 at x = 1.
-y =
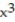 - 3
- 3 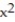 + 6x - 8
+ 6x - 8A) None
B) Absolute minimum is 4 at x = -1.
C) Absolute maximum is 4 at x = 2.
D) Absolute maximum is 4 at x = 1.

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
29
Find the extreme values of the function and where they occur.
-y =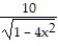
A) Absolute minimum is 0 at x = 1.
B) Absolute maximum is 10 at x = 2.
C) Absolute minimum is 10 at x = 0.
D) Absolute maximum is 10 at x = -2.
-y =
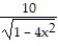
A) Absolute minimum is 0 at x = 1.
B) Absolute maximum is 10 at x = 2.
C) Absolute minimum is 10 at x = 0.
D) Absolute maximum is 10 at x = -2.

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
30
Find the extreme values of the function and where they occur.
-y =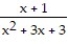
A) None
B) Absolute maximum is 1/3 at x = 0; absolute minimum is - 1 at x = -2.
C) Absolute maximum is 3 at x = 0; absolute minimum is 1/3 at x = -2.
D) Absolute maximum is -1/3 at x = 0; absolute minimum is 1 at x = -2.
-y =
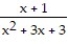
A) None
B) Absolute maximum is 1/3 at x = 0; absolute minimum is - 1 at x = -2.
C) Absolute maximum is 3 at x = 0; absolute minimum is 1/3 at x = -2.
D) Absolute maximum is -1/3 at x = 0; absolute minimum is 1 at x = -2.

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
31
Find the extreme values of the function and where they occur.
-y =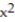
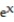
A) Absolute minimum value is 0 at x = 0; no maximum value.
B)Absolute minimum value is 0 at x = 0, absolute maximum value is 4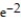 at x = -2.
at x = -2.
C) Absolute minimum value is 4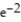 at x = -2; no maximum value.
at x = -2; no maximum value.
D) None
-y =
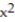
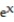
A) Absolute minimum value is 0 at x = 0; no maximum value.
B)Absolute minimum value is 0 at x = 0, absolute maximum value is 4
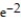 at x = -2.
at x = -2.C) Absolute minimum value is 4
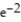 at x = -2; no maximum value.
at x = -2; no maximum value.D) None

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
32
Find the extreme values of the function and where they occur.
-y =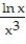
A) Absolute minimum value is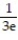 at x =
at x = 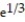 ; no maximum value.
; no maximum value.
B) Absolute maximum value is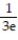 at x =
at x = 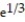 ; no minimum value.
; no minimum value.
C) Absolute maximum value is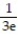 at x =
at x = 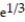 ; absolute minimum value is 0 at x = 1.
; absolute minimum value is 0 at x = 1.
D) None
-y =
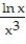
A) Absolute minimum value is
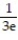 at x =
at x = 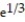 ; no maximum value.
; no maximum value.B) Absolute maximum value is
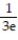 at x =
at x = 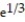 ; no minimum value.
; no minimum value.C) Absolute maximum value is
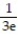 at x =
at x = 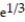 ; absolute minimum value is 0 at x = 1.
; absolute minimum value is 0 at x = 1.D) None

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
33
Find the extreme values of the function and where they occur.
-y =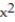
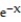 + 2x
+ 2x 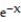
A)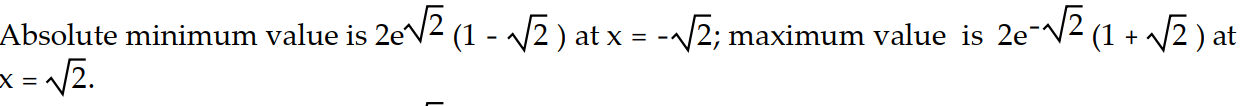
B)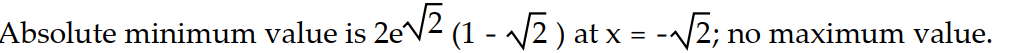
C)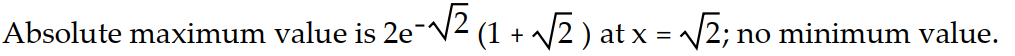
D) None
-y =
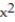
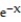 + 2x
+ 2x 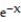
A)
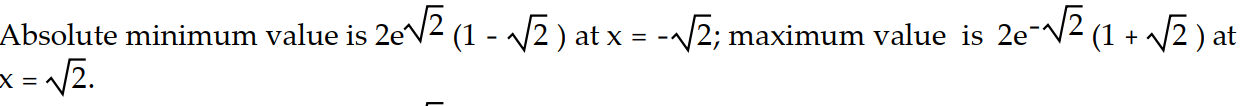
B)
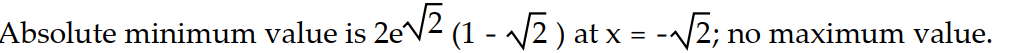
C)
D) None

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
34
Provide an appropriate response.
-Imagine there is a function for which (x) = 0 for all x. Does such a function exist? Is it reasonable to say that all values of x are critical points for such a function? Is it reasonable to say that all values of x are extreme values for such a function. Give reasons for your answer.
(x) = 0 for all x. Does such a function exist? Is it reasonable to say that all values of x are critical points for such a function? Is it reasonable to say that all values of x are extreme values for such a function. Give reasons for your answer.
-Imagine there is a function for which
 (x) = 0 for all x. Does such a function exist? Is it reasonable to say that all values of x are critical points for such a function? Is it reasonable to say that all values of x are extreme values for such a function. Give reasons for your answer.
(x) = 0 for all x. Does such a function exist? Is it reasonable to say that all values of x are critical points for such a function? Is it reasonable to say that all values of x are extreme values for such a function. Give reasons for your answer.
Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
35
Provide an appropriate response.
-Consider the quartic function f(x) = a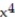 + b
+ b 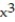 + c
+ c 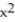 + dx + e, a ≠ 0. Must this function have at least one critical point? Give reasons for your answer. (Hint: Must
+ dx + e, a ≠ 0. Must this function have at least one critical point? Give reasons for your answer. (Hint: Must 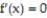 for some x?) How many local extreme values can f have?
for some x?) How many local extreme values can f have?
-Consider the quartic function f(x) = a
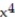 + b
+ b 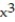 + c
+ c 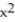 + dx + e, a ≠ 0. Must this function have at least one critical point? Give reasons for your answer. (Hint: Must
+ dx + e, a ≠ 0. Must this function have at least one critical point? Give reasons for your answer. (Hint: Must 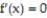 for some x?) How many local extreme values can f have?
for some x?) How many local extreme values can f have?
Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
36
Determine whether the function satisfies the hypotheses of the Mean Value Theorem for the given interval.
-f(x) =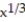 ,
, 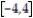
-f(x) =
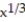 ,
, 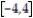

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
37
Determine whether the function satisfies the hypotheses of the Mean Value Theorem for the given interval.
-g(x) =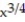 ,
, 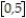
-g(x) =
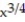 ,
, 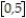

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
38
Determine whether the function satisfies the hypotheses of the Mean Value Theorem for the given interval.
-s(t) =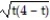 ,
, 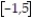
-s(t) =
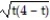 ,
, 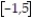

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
39
Find the value or values of c that satisfy the equation ![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = + 2x + 1, [ -3, -2]</strong> A) -3, -2 B) - 5/2, 5/2 C) 0, - 5/2 D) - 5/2](https://storage.examlex.com/TB9662/11ee9522_3416_08b0_bdb6_3b3290666101_TB9662_11.jpg) =
= ![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = + 2x + 1, [ -3, -2]</strong> A) -3, -2 B) - 5/2, 5/2 C) 0, - 5/2 D) - 5/2](https://storage.examlex.com/TB9662/11ee9522_3416_08b1_bdb6_a738a1f77c49_TB9662_11.jpg) (c) in the conclusion of the Mean Value Theorem for the function and interval.
(c) in the conclusion of the Mean Value Theorem for the function and interval.
-f(x) =![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = + 2x + 1, [ -3, -2]</strong> A) -3, -2 B) - 5/2, 5/2 C) 0, - 5/2 D) - 5/2](https://storage.examlex.com/TB9662/11ee9522_3416_08b2_bdb6_532cc9f6e27f_TB9662_11.jpg) + 2x + 1, [ -3, -2]
+ 2x + 1, [ -3, -2]
A) -3, -2
B) - 5/2, 5/2
C) 0, - 5/2
D) - 5/2
![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = + 2x + 1, [ -3, -2]</strong> A) -3, -2 B) - 5/2, 5/2 C) 0, - 5/2 D) - 5/2](https://storage.examlex.com/TB9662/11ee9522_3416_08b0_bdb6_3b3290666101_TB9662_11.jpg) =
= ![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = + 2x + 1, [ -3, -2]</strong> A) -3, -2 B) - 5/2, 5/2 C) 0, - 5/2 D) - 5/2](https://storage.examlex.com/TB9662/11ee9522_3416_08b1_bdb6_a738a1f77c49_TB9662_11.jpg) (c) in the conclusion of the Mean Value Theorem for the function and interval.
(c) in the conclusion of the Mean Value Theorem for the function and interval.-f(x) =
![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = + 2x + 1, [ -3, -2]</strong> A) -3, -2 B) - 5/2, 5/2 C) 0, - 5/2 D) - 5/2](https://storage.examlex.com/TB9662/11ee9522_3416_08b2_bdb6_532cc9f6e27f_TB9662_11.jpg) + 2x + 1, [ -3, -2]
+ 2x + 1, [ -3, -2]A) -3, -2
B) - 5/2, 5/2
C) 0, - 5/2
D) - 5/2

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
40
Find the value or values of c that satisfy the equation 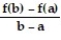 =
=  (c) in the conclusion of the Mean Value Theorem for the function and interval.
(c) in the conclusion of the Mean Value Theorem for the function and interval.
-f(x) = x +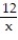 ,
, 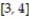
A) 0, 2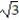
B) -2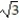 , 2
, 2 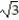
C) 3, 4
D) 2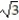
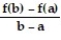 =
=  (c) in the conclusion of the Mean Value Theorem for the function and interval.
(c) in the conclusion of the Mean Value Theorem for the function and interval.-f(x) = x +
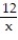 ,
, 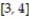
A) 0, 2
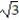
B) -2
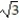 , 2
, 2 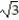
C) 3, 4
D) 2
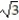

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
41
Find the value or values of c that satisfy the equation ![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = x, [-1, 1]</strong> A) c = 0, B) c = - , C) c = D) c = - , 0 ,](https://storage.examlex.com/TB9662/11ee9522_3416_08b0_bdb6_3b3290666101_TB9662_11.jpg) =
= ![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = x, [-1, 1]</strong> A) c = 0, B) c = - , C) c = D) c = - , 0 ,](https://storage.examlex.com/TB9662/11ee9522_3416_08b1_bdb6_a738a1f77c49_TB9662_11.jpg) (c) in the conclusion of the Mean Value Theorem for the function and interval.
(c) in the conclusion of the Mean Value Theorem for the function and interval.
-f(x) =![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = x, [-1, 1]</strong> A) c = 0, B) c = - , C) c = D) c = - , 0 ,](https://storage.examlex.com/TB9662/11ee9522_3416_56d9_bdb6_83f79ffa6701_TB9662_11.jpg) x, [-1, 1]
x, [-1, 1]
A) c = 0,![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = x, [-1, 1]</strong> A) c = 0, B) c = - , C) c = D) c = - , 0 ,](https://storage.examlex.com/TB9662/11ee9522_3416_7dea_bdb6_13fe3908ae93_TB9662_11.jpg)
B) c = -![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = x, [-1, 1]</strong> A) c = 0, B) c = - , C) c = D) c = - , 0 ,](https://storage.examlex.com/TB9662/11ee9522_3416_7deb_bdb6_7b7dd4d1b17c_TB9662_11.jpg) ,
, ![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = x, [-1, 1]</strong> A) c = 0, B) c = - , C) c = D) c = - , 0 ,](https://storage.examlex.com/TB9662/11ee9522_3416_7dec_bdb6_ab6c0454cd8c_TB9662_11.jpg)
C) c =![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = x, [-1, 1]</strong> A) c = 0, B) c = - , C) c = D) c = - , 0 ,](https://storage.examlex.com/TB9662/11ee9522_3416_7ded_bdb6_2dd572601352_TB9662_11.jpg)
D) c = -![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = x, [-1, 1]</strong> A) c = 0, B) c = - , C) c = D) c = - , 0 ,](https://storage.examlex.com/TB9662/11ee9522_3416_7dee_bdb6_e38a7442f31f_TB9662_11.jpg) , 0 ,
, 0 , ![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = x, [-1, 1]</strong> A) c = 0, B) c = - , C) c = D) c = - , 0 ,](https://storage.examlex.com/TB9662/11ee9522_3416_a4ff_bdb6_2bbb5be17ca4_TB9662_11.jpg)
![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = x, [-1, 1]</strong> A) c = 0, B) c = - , C) c = D) c = - , 0 ,](https://storage.examlex.com/TB9662/11ee9522_3416_08b0_bdb6_3b3290666101_TB9662_11.jpg) =
= ![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = x, [-1, 1]</strong> A) c = 0, B) c = - , C) c = D) c = - , 0 ,](https://storage.examlex.com/TB9662/11ee9522_3416_08b1_bdb6_a738a1f77c49_TB9662_11.jpg) (c) in the conclusion of the Mean Value Theorem for the function and interval.
(c) in the conclusion of the Mean Value Theorem for the function and interval.-f(x) =
![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = x, [-1, 1]</strong> A) c = 0, B) c = - , C) c = D) c = - , 0 ,](https://storage.examlex.com/TB9662/11ee9522_3416_56d9_bdb6_83f79ffa6701_TB9662_11.jpg) x, [-1, 1]
x, [-1, 1]A) c = 0,
![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = x, [-1, 1]</strong> A) c = 0, B) c = - , C) c = D) c = - , 0 ,](https://storage.examlex.com/TB9662/11ee9522_3416_7dea_bdb6_13fe3908ae93_TB9662_11.jpg)
B) c = -
![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = x, [-1, 1]</strong> A) c = 0, B) c = - , C) c = D) c = - , 0 ,](https://storage.examlex.com/TB9662/11ee9522_3416_7deb_bdb6_7b7dd4d1b17c_TB9662_11.jpg) ,
, ![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = x, [-1, 1]</strong> A) c = 0, B) c = - , C) c = D) c = - , 0 ,](https://storage.examlex.com/TB9662/11ee9522_3416_7dec_bdb6_ab6c0454cd8c_TB9662_11.jpg)
C) c =
![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = x, [-1, 1]</strong> A) c = 0, B) c = - , C) c = D) c = - , 0 ,](https://storage.examlex.com/TB9662/11ee9522_3416_7ded_bdb6_2dd572601352_TB9662_11.jpg)
D) c = -
![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = x, [-1, 1]</strong> A) c = 0, B) c = - , C) c = D) c = - , 0 ,](https://storage.examlex.com/TB9662/11ee9522_3416_7dee_bdb6_e38a7442f31f_TB9662_11.jpg) , 0 ,
, 0 , ![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = x, [-1, 1]</strong> A) c = 0, B) c = - , C) c = D) c = - , 0 ,](https://storage.examlex.com/TB9662/11ee9522_3416_a4ff_bdb6_2bbb5be17ca4_TB9662_11.jpg)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
42
Find the value or values of c that satisfy the equation ![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = ln (x - 3), [ 4, 8]</strong> A) c = + 3 B) c = + 3 C) c = + 3 D) c = + 3](https://storage.examlex.com/TB9662/11ee9522_3416_08b0_bdb6_3b3290666101_TB9662_11.jpg) =
= ![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = ln (x - 3), [ 4, 8]</strong> A) c = + 3 B) c = + 3 C) c = + 3 D) c = + 3](https://storage.examlex.com/TB9662/11ee9522_3416_08b1_bdb6_a738a1f77c49_TB9662_11.jpg) (c) in the conclusion of the Mean Value Theorem for the function and interval.
(c) in the conclusion of the Mean Value Theorem for the function and interval.
-f(x) = ln (x - 3), [ 4, 8]
A) c =![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = ln (x - 3), [ 4, 8]</strong> A) c = + 3 B) c = + 3 C) c = + 3 D) c = + 3](https://storage.examlex.com/TB9662/11ee9522_3416_a500_bdb6_2fea49acb931_TB9662_11.jpg) + 3
+ 3
B) c =![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = ln (x - 3), [ 4, 8]</strong> A) c = + 3 B) c = + 3 C) c = + 3 D) c = + 3](https://storage.examlex.com/TB9662/11ee9522_3416_a501_bdb6_8369302daa7f_TB9662_11.jpg) + 3
+ 3
C) c =![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = ln (x - 3), [ 4, 8]</strong> A) c = + 3 B) c = + 3 C) c = + 3 D) c = + 3](https://storage.examlex.com/TB9662/11ee9522_3416_cc12_bdb6_cd8ae0114412_TB9662_11.jpg) + 3
+ 3
D) c =![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = ln (x - 3), [ 4, 8]</strong> A) c = + 3 B) c = + 3 C) c = + 3 D) c = + 3](https://storage.examlex.com/TB9662/11ee9522_3416_cc13_bdb6_4d09cc67facd_TB9662_11.jpg) + 3
+ 3
![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = ln (x - 3), [ 4, 8]</strong> A) c = + 3 B) c = + 3 C) c = + 3 D) c = + 3](https://storage.examlex.com/TB9662/11ee9522_3416_08b0_bdb6_3b3290666101_TB9662_11.jpg) =
= ![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = ln (x - 3), [ 4, 8]</strong> A) c = + 3 B) c = + 3 C) c = + 3 D) c = + 3](https://storage.examlex.com/TB9662/11ee9522_3416_08b1_bdb6_a738a1f77c49_TB9662_11.jpg) (c) in the conclusion of the Mean Value Theorem for the function and interval.
(c) in the conclusion of the Mean Value Theorem for the function and interval.-f(x) = ln (x - 3), [ 4, 8]
A) c =
![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = ln (x - 3), [ 4, 8]</strong> A) c = + 3 B) c = + 3 C) c = + 3 D) c = + 3](https://storage.examlex.com/TB9662/11ee9522_3416_a500_bdb6_2fea49acb931_TB9662_11.jpg) + 3
+ 3B) c =
![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = ln (x - 3), [ 4, 8]</strong> A) c = + 3 B) c = + 3 C) c = + 3 D) c = + 3](https://storage.examlex.com/TB9662/11ee9522_3416_a501_bdb6_8369302daa7f_TB9662_11.jpg) + 3
+ 3C) c =
![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = ln (x - 3), [ 4, 8]</strong> A) c = + 3 B) c = + 3 C) c = + 3 D) c = + 3](https://storage.examlex.com/TB9662/11ee9522_3416_cc12_bdb6_cd8ae0114412_TB9662_11.jpg) + 3
+ 3D) c =
![<strong>Find the value or values of c that satisfy the equation = (c) in the conclusion of the Mean Value Theorem for the function and interval. -f(x) = ln (x - 3), [ 4, 8]</strong> A) c = + 3 B) c = + 3 C) c = + 3 D) c = + 3](https://storage.examlex.com/TB9662/11ee9522_3416_cc13_bdb6_4d09cc67facd_TB9662_11.jpg) + 3
+ 3
Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
43
Provide an appropriate response.
-It took 20 seconds for the temperature to rise from 4° F to 166° F when a thermometer was taken from a freezer and placed in boiling water. Although we do not have detailed knowledge about the rate of temperature increase, we can know for certain that, at some time, the temperature was increasing at a rate of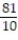 ° F/sec. Explain.
° F/sec. Explain.
-It took 20 seconds for the temperature to rise from 4° F to 166° F when a thermometer was taken from a freezer and placed in boiling water. Although we do not have detailed knowledge about the rate of temperature increase, we can know for certain that, at some time, the temperature was increasing at a rate of
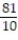 ° F/sec. Explain.
° F/sec. Explain.
Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
44
Solve the problem.
-Select an appropriate graph of a twice-differentiable function y = f(x) that passes through the points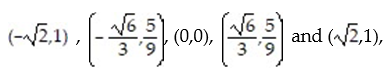 and whose first two derivatives have the following sign patterns.
and whose first two derivatives have the following sign patterns.
A)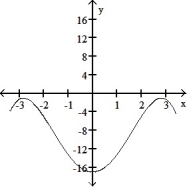
B)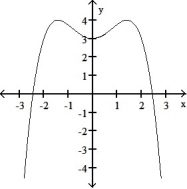
C)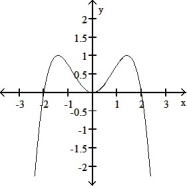
D)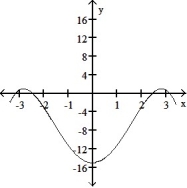
-Select an appropriate graph of a twice-differentiable function y = f(x) that passes through the points
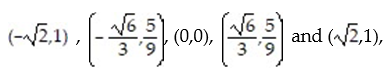 and whose first two derivatives have the following sign patterns.
and whose first two derivatives have the following sign patterns.A)

B)

C)

D)


Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
45
Write the word or phrase that best completes each statement or answers the question.
-Sketch a continuous curve y = f(x) with the following properties: f(2) = 3; (x) > 0 for x > 4; and
(x) > 0 for x > 4; and  (x) < 0 for x < 4 .
(x) < 0 for x < 4 .
-Sketch a continuous curve y = f(x) with the following properties: f(2) = 3;
 (x) > 0 for x > 4; and
(x) > 0 for x > 4; and  (x) < 0 for x < 4 .
(x) < 0 for x < 4 .
Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
46
Choose the one alternative that best completes the statement or answers the question.
-The graph below shows the first derivative of a function y = f(x). Select a possible graph of f that passes through the point P.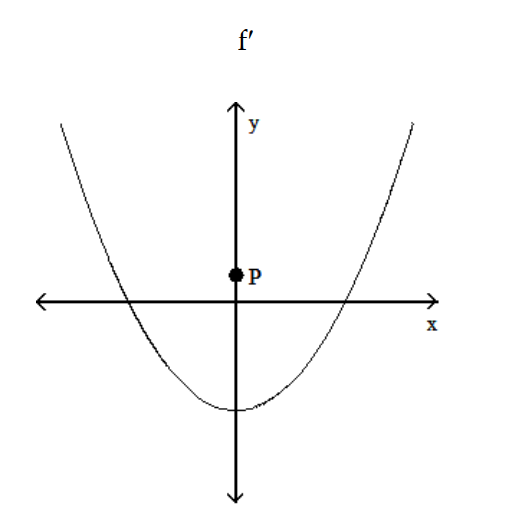
A)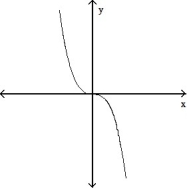
B)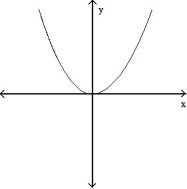
C)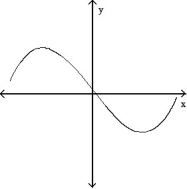
D)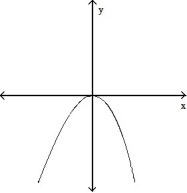
-The graph below shows the first derivative of a function y = f(x). Select a possible graph of f that passes through the point P.

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
47
Choose the one alternative that best completes the statement or answers the question.
-The graph below shows the first derivative of a function y = f(x). Select a possible graph f that passes through the point P.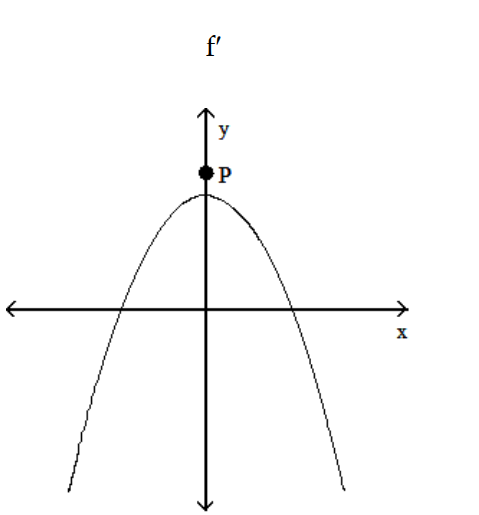
A)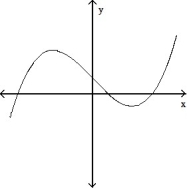
B)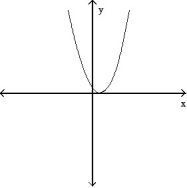
C)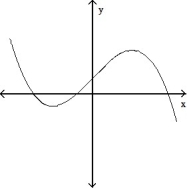
D)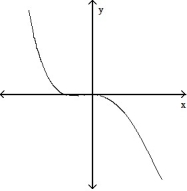
-The graph below shows the first derivative of a function y = f(x). Select a possible graph f that passes through the point P.

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
48
Choose the one alternative that best completes the statement or answers the question.
-The graph below shows the first derivative of a function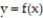 . Select a possible graph f that passes through the point P.
. Select a possible graph f that passes through the point P. 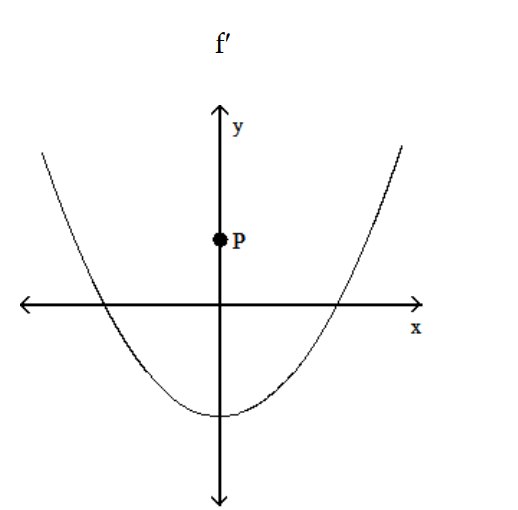
A)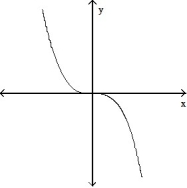
B)
C)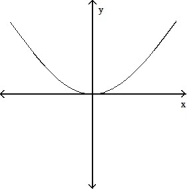
D)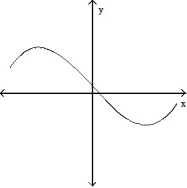
-The graph below shows the first derivative of a function
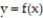 . Select a possible graph f that passes through the point P.
. Select a possible graph f that passes through the point P. 
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
49
Find the largest open interval where the function is changing as requested.
-Increasing f(x) = x2 -
x2 - 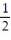 x
x
A) (-1, 1)
B) (- , -1)
C) (- , )
D) (1, )
-Increasing f(x) =
 x2 -
x2 - 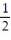 x
xA) (-1, 1)
B) (- , -1)
C) (- , )
D) (1, )

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
50
Find the largest open interval where the function is changing as requested.
-Increasing f(x) = x2 - 2x + 1
A) (0, )
B) (1, )
C) (- , 1)
D) (- , 0)
-Increasing f(x) = x2 - 2x + 1
A) (0, )
B) (1, )
C) (- , 1)
D) (- , 0)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
51
Find the largest open interval where the function is changing as requested.
-Increasing y = (x2 - 9)2
A) (-3, 0)
B) (- , 0)
C) (-3, 3)
D) (3, )
-Increasing y = (x2 - 9)2
A) (-3, 0)
B) (- , 0)
C) (-3, 3)
D) (3, )

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
52
Find the largest open interval where the function is changing as requested.
-Increasing f(x) =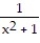
A) (1, )
B) (- , 0)
C) (- , 1)
D) (0, )
-Increasing f(x) =
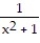
A) (1, )
B) (- , 0)
C) (- , 1)
D) (0, )

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
53
Find the largest open interval where the function is changing as requested.
-Decreasing f(x) =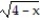
A) (- , -4)
B) (4, )
C) (- , 4)
D) (-4, )
-Decreasing f(x) =
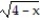
A) (- , -4)
B) (4, )
C) (- , 4)
D) (-4, )

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
54
Find the largest open interval where the function is changing as requested.
-Decreasing f(x) =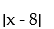
A) (- , -8)
B) (8, )
C) (- , 8)
D) (-8, )
-Decreasing f(x) =
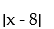
A) (- , -8)
B) (8, )
C) (- , 8)
D) (-8, )

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
55
Find the largest open interval where the function is changing as requested.
-Decreasing y =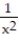 + 7
+ 7
A) (-7, 0)
B) (0, )
C) (7, )
D) (-7, 7)
-Decreasing y =
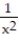 + 7
+ 7A) (-7, 0)
B) (0, )
C) (7, )
D) (-7, 7)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
56
Find the largest open interval where the function is changing as requested.
-Decreasing f(x) = -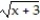
A) (3, )
B) (-3, )
C) (- , 3)
D) (- , -3)
-Decreasing f(x) = -
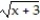
A) (3, )
B) (-3, )
C) (- , 3)
D) (- , -3)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
57
Find the largest open interval where the function is changing as requested.
-Decreasing f(x) = x3 - 4x
A)
B)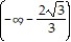
C)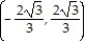
D)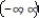
-Decreasing f(x) = x3 - 4x
A)
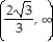
B)
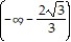
C)
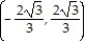
D)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
58
Solve the problem.
-The graphs below show the first and second derivatives of a function . Select a possible graph f that passes through the point P.
. Select a possible graph f that passes through the point P. 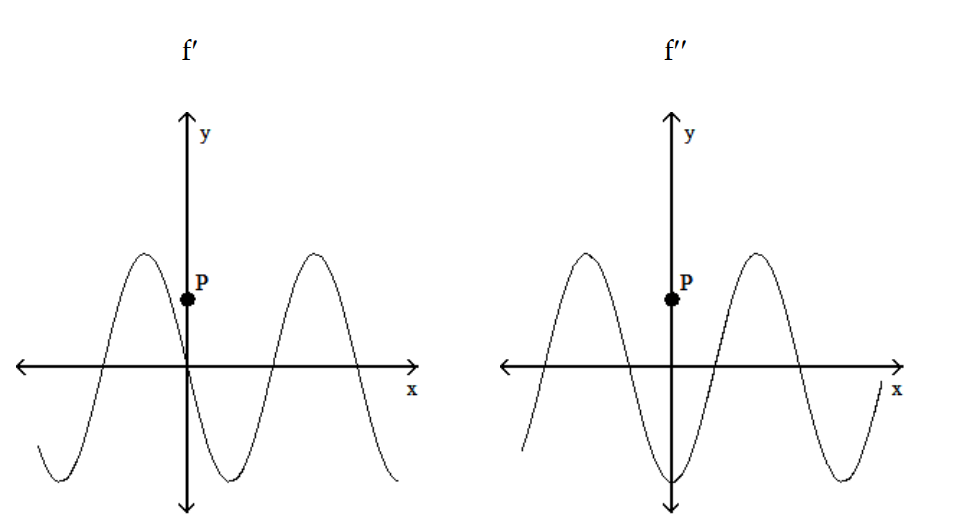
A)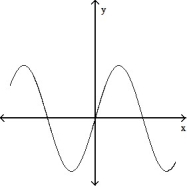
B)
C)
D)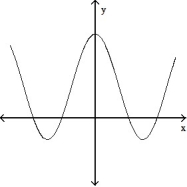
-The graphs below show the first and second derivatives of a function
 . Select a possible graph f that passes through the point P.
. Select a possible graph f that passes through the point P. 
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
59
Solve the problem.
-The graphs below show the first and second derivatives of a function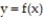 . Select a possible graph of f that passes through point P.
. Select a possible graph of f that passes through point P. 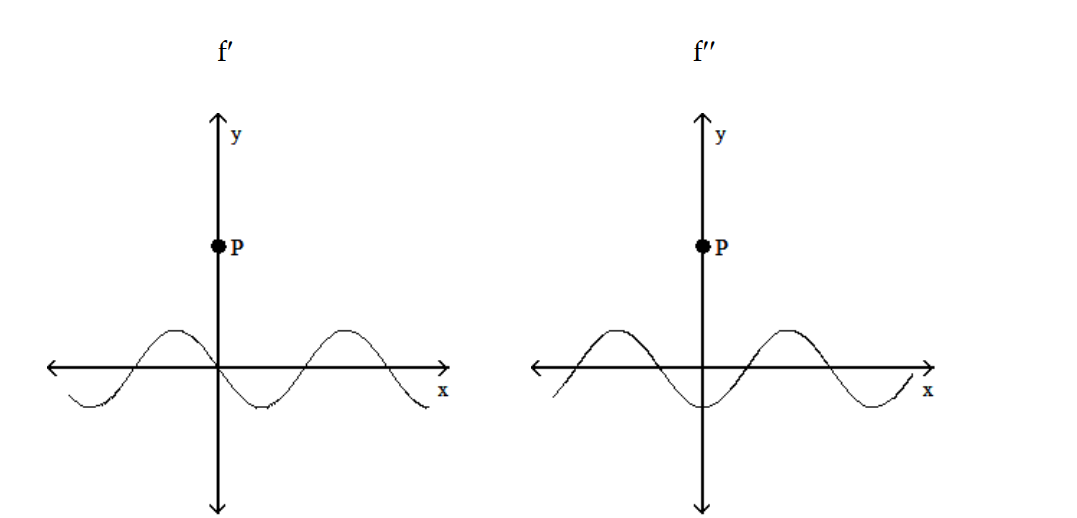
A)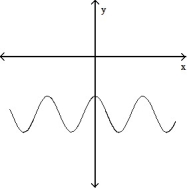
B)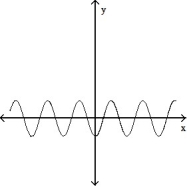
C)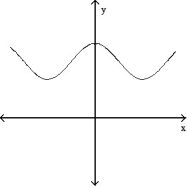
D)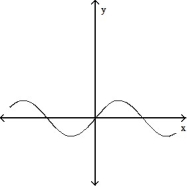
-The graphs below show the first and second derivatives of a function
 . Select a possible graph of f that passes through point P.
. Select a possible graph of f that passes through point P. 
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
60
Solve the problem.
-The graphs below show the first and second derivatives of a function . Select a possible graph f that passes through the point P.
. Select a possible graph f that passes through the point P. 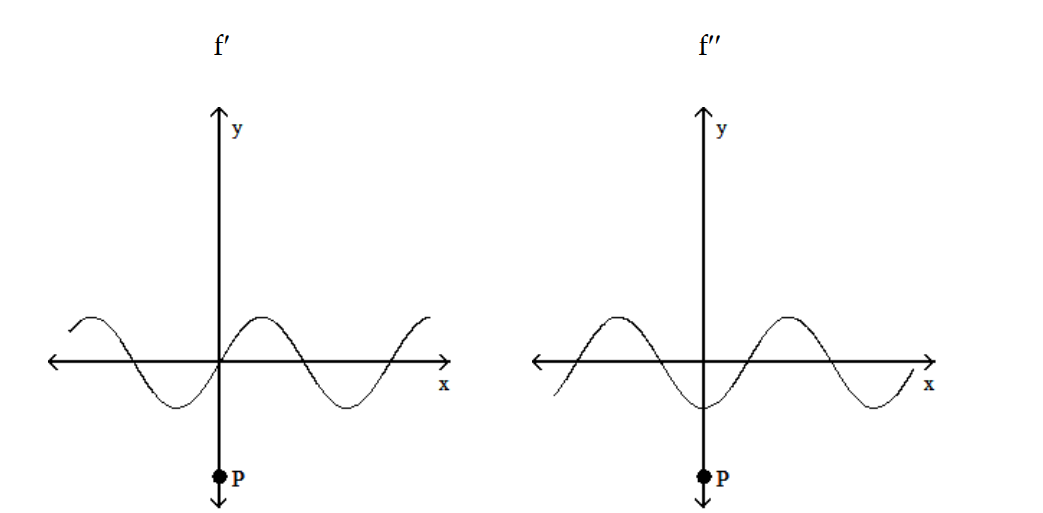
A)
B)
C)
D)
-The graphs below show the first and second derivatives of a function
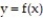 . Select a possible graph f that passes through the point P.
. Select a possible graph f that passes through the point P. 
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
61
Use the graph of the function f(x) to locate the local extrema and identify the intervals where the function is concave up and concave down.
-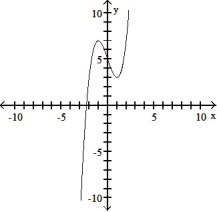
A) Local minimum at x = 1; local maximum at x = -1; concave down on (0, ); concave up on (- , 0)
B) Local minimum at x = 1; local maximum at x = -1; concave up on (0, ); concave down on (- , 0)
C) Local minimum at x = 1; local maximum at x = -1; concave down on (- , )
D) Local minimum at x = 1; local maximum at x = -1; concave up on (- , )
-

A) Local minimum at x = 1; local maximum at x = -1; concave down on (0, ); concave up on (- , 0)
B) Local minimum at x = 1; local maximum at x = -1; concave up on (0, ); concave down on (- , 0)
C) Local minimum at x = 1; local maximum at x = -1; concave down on (- , )
D) Local minimum at x = 1; local maximum at x = -1; concave up on (- , )

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
62
Use the graph of the function f(x) to locate the local extrema and identify the intervals where the function is concave up and concave down.
-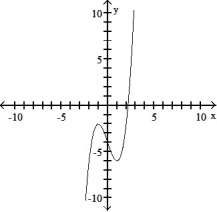
A) Local minimum at x = 1; local maximum at x =-1; concave up on (0, ); concave down on (- , 0)
B)Local minimum at x = 1; local maximum at x =-1; concave down on (0, ); concave up on (- 0)
C) Local maximum at x = 1; local minimum at x =-1; concave up on (- , )
D) Local maximum at x = 1; local minimum at x =-1; concave up on (0, ); concave down on (- , 0)
-

A) Local minimum at x = 1; local maximum at x =-1; concave up on (0, ); concave down on (- , 0)
B)Local minimum at x = 1; local maximum at x =-1; concave down on (0, ); concave up on (- 0)
C) Local maximum at x = 1; local minimum at x =-1; concave up on (- , )
D) Local maximum at x = 1; local minimum at x =-1; concave up on (0, ); concave down on (- , 0)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
63
Use the graph of the function f(x) to locate the local extrema and identify the intervals where the function is concave up and concave down.
-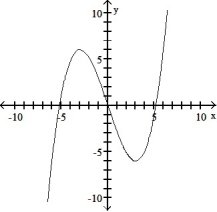
A) Local minimum at x = 3; local maximum at x = -3 ; concave down on (0, ); concave up on (- , 0)
B) Local minimum at x = 3; local maximum at x = -3 ; concave up on (0, -3) and (3, ); concave down on (-3, 3)
C) Local minimum at x = 3; local maximum at x = -3 ; concave up on (0, ); concave down on (- , 0)
D) Local maximum at x = 3; local minimum at x = -3 ; concave up on (0, -3) and (3, ); concave down on (-3, 3)
-

A) Local minimum at x = 3; local maximum at x = -3 ; concave down on (0, ); concave up on (- , 0)
B) Local minimum at x = 3; local maximum at x = -3 ; concave up on (0, -3) and (3, ); concave down on (-3, 3)
C) Local minimum at x = 3; local maximum at x = -3 ; concave up on (0, ); concave down on (- , 0)
D) Local maximum at x = 3; local minimum at x = -3 ; concave up on (0, -3) and (3, ); concave down on (-3, 3)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
64
Use the graph of the function f(x) to locate the local extrema and identify the intervals where the function is concave up and concave down.
-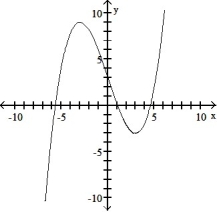
A) Local minimum at x = 3 ; local maximum at x = -3 ; concave up on (- , -3) and (3, ); concave down on (-3, 3)
B) Local minimum at x = 3 ; local maximum at x = -3 ; concave down on (- -3) and (3, ); concave up on (-3, 3)
C) Local minimum at x = 3 ; local maximum at x = -3 ; concave up on (0, ); concave down on (- , 0)
D) Local minimum at x = 3 ; local maximum at x = -3 ; concave down on (0, ); concave up on (- , 0)
-

A) Local minimum at x = 3 ; local maximum at x = -3 ; concave up on (- , -3) and (3, ); concave down on (-3, 3)
B) Local minimum at x = 3 ; local maximum at x = -3 ; concave down on (- -3) and (3, ); concave up on (-3, 3)
C) Local minimum at x = 3 ; local maximum at x = -3 ; concave up on (0, ); concave down on (- , 0)
D) Local minimum at x = 3 ; local maximum at x = -3 ; concave down on (0, ); concave up on (- , 0)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
65
Use the graph of the function f(x) to locate the local extrema and identify the intervals where the function is concave up and concave down.
-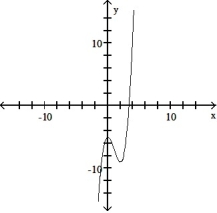
A) Local minimum at x = 0; local maximum at x = 2; concave up on (0, ); concave down on (- , 0)
B) Local minimum at x = 0; local maximum at x = 2; concave down on (0, ); concave up on (- , 0)
C) Local minimum at x = 2; local maximum at x = 0; concave down on (0, ); concave up on (- , 0)
D) Local minimum at x = 2; local maximum at x = 0; concave up on (0, ); concave down on (- , 0)
-

A) Local minimum at x = 0; local maximum at x = 2; concave up on (0, ); concave down on (- , 0)
B) Local minimum at x = 0; local maximum at x = 2; concave down on (0, ); concave up on (- , 0)
C) Local minimum at x = 2; local maximum at x = 0; concave down on (0, ); concave up on (- , 0)
D) Local minimum at x = 2; local maximum at x = 0; concave up on (0, ); concave down on (- , 0)

Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
66
Solve the problem.
-Using the following properties of a twice-differentiable function y = f(x), select a possible graph of f.

A)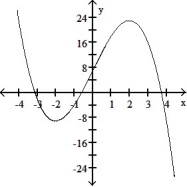
B)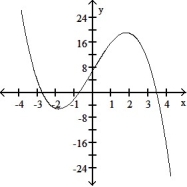
C)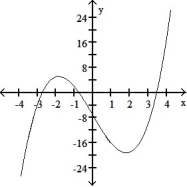
D)
-Using the following properties of a twice-differentiable function y = f(x), select a possible graph of f.

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
67
Graph the equation. Include the coordinates of any local extreme points and inflection points.
-y = 3x2 + 24x
A) local minimum: ( 8, -24) no inflection points
B) local minimum: ( -8, -24) no inflection points
C)local minimum: ( -4, -48) no inflection points
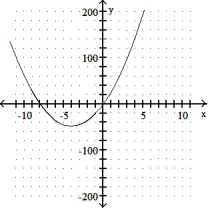
D) local minimum: ( 4, -48) no inflection points
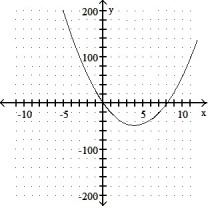
-y = 3x2 + 24x

A) local minimum: ( 8, -24) no inflection points

B) local minimum: ( -8, -24) no inflection points

C)local minimum: ( -4, -48) no inflection points

D) local minimum: ( 4, -48) no inflection points


Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
68
Graph the equation. Include the coordinates of any local extreme points and inflection points.
-y =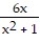
A)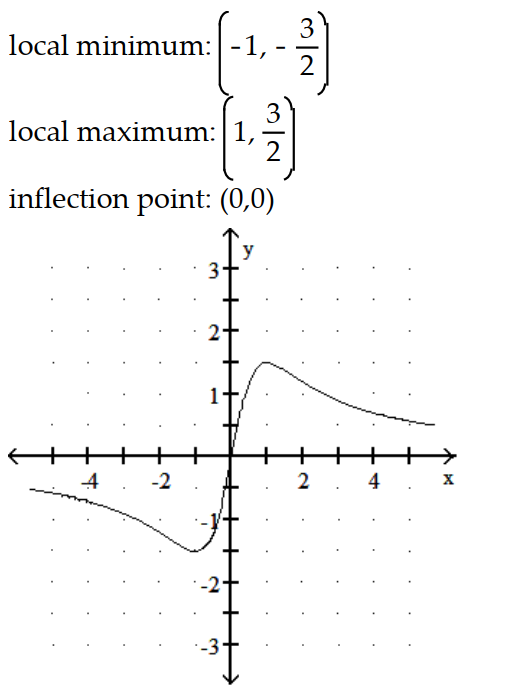
B)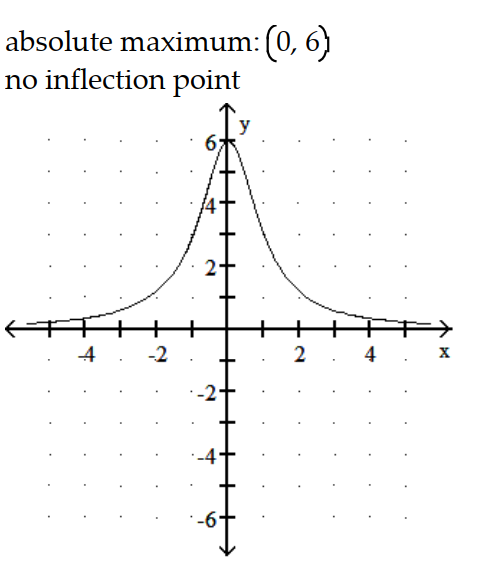
C)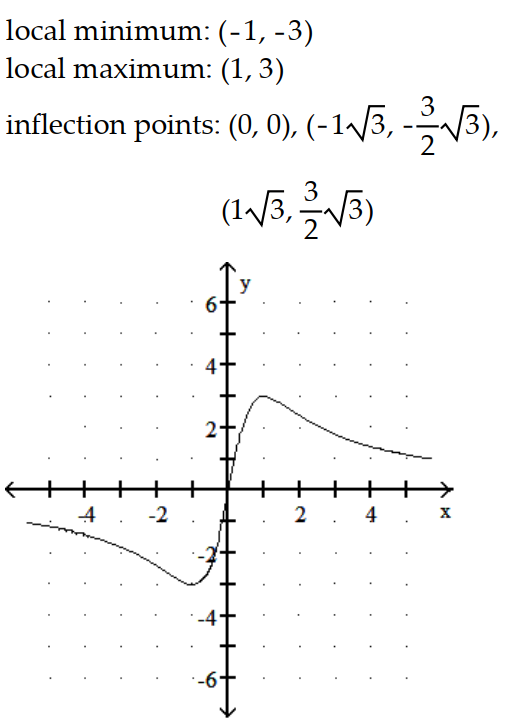
D)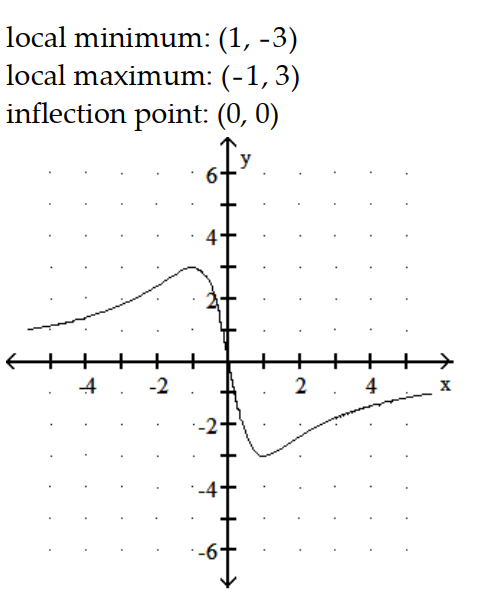
-y =
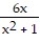

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
69
Graph the equation. Include the coordinates of any local extreme points and inflection points.
-y = 2x3 - 15x2 + 24x
A)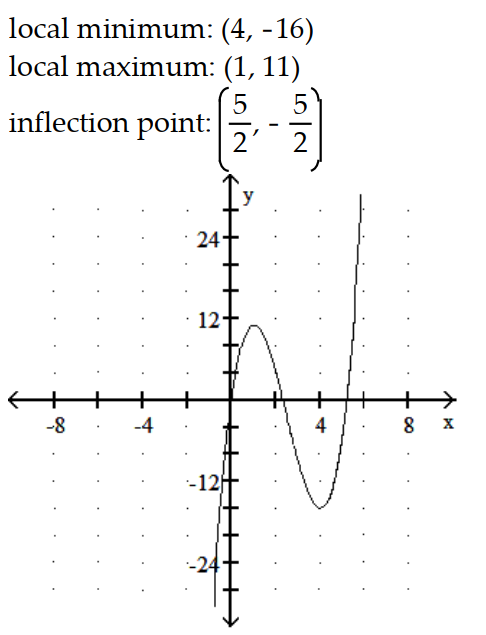
B)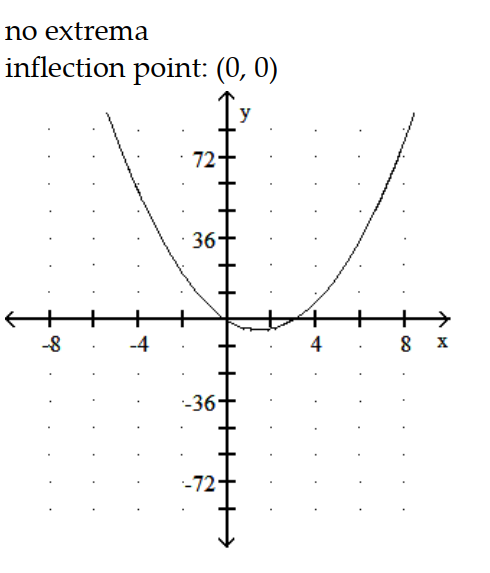
C)
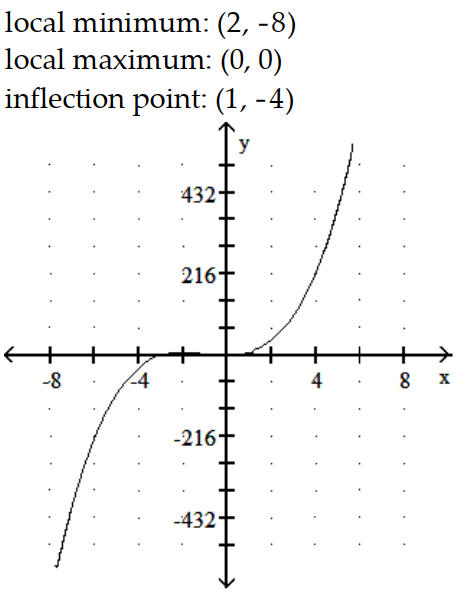
D)
-y = 2x3 - 15x2 + 24x

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
70
Graph the equation. Include the coordinates of any local extreme points and inflection points.
-y = x1/3(x2 - 63)
A)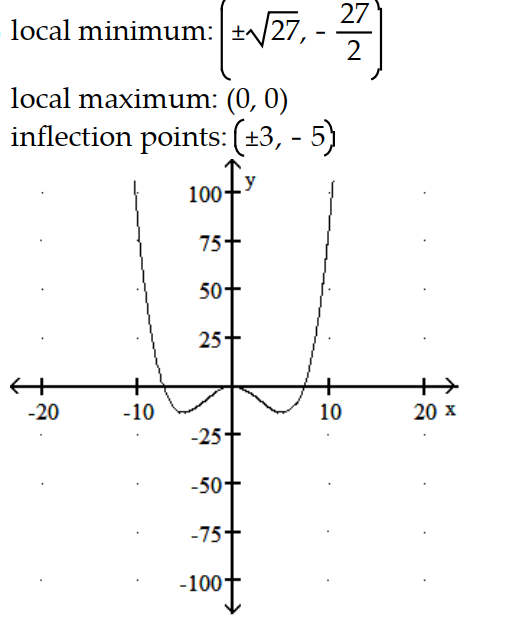
B)
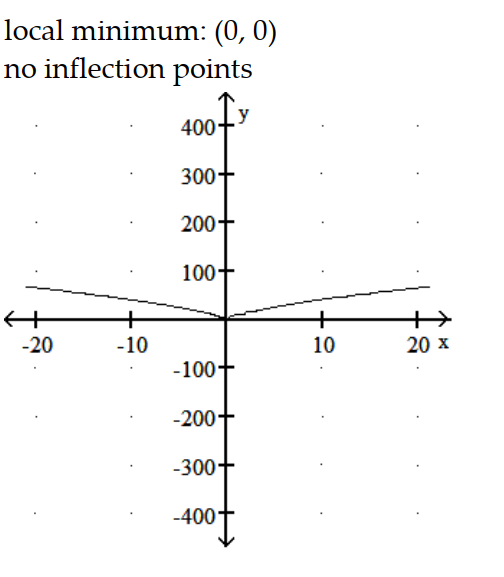
C)
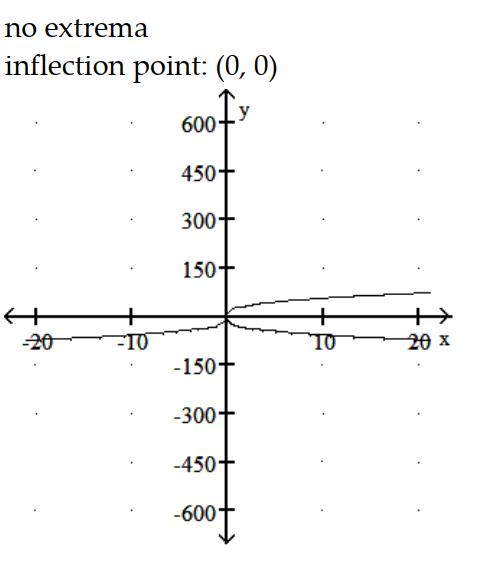
D)
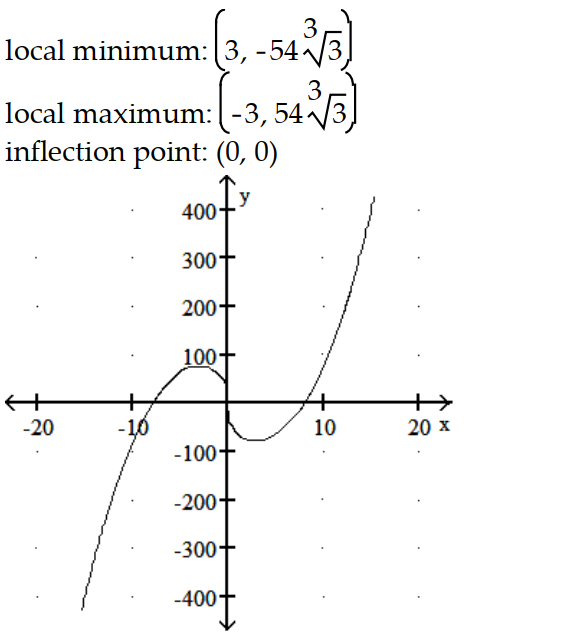
-y = x1/3(x2 - 63)

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
71
Graph the equation. Include the coordinates of any local extreme points and inflection points.
-y =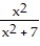
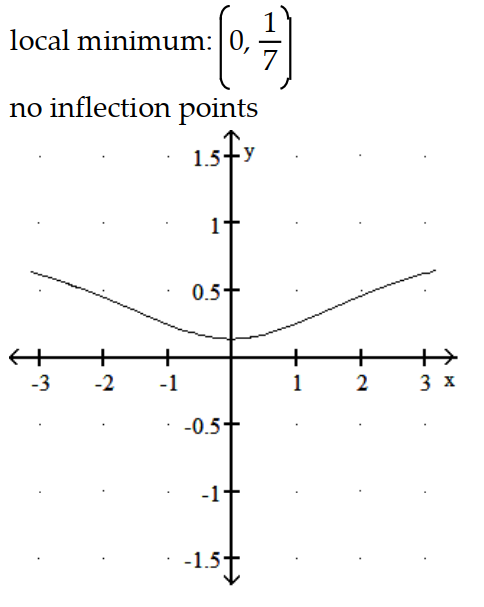
A)
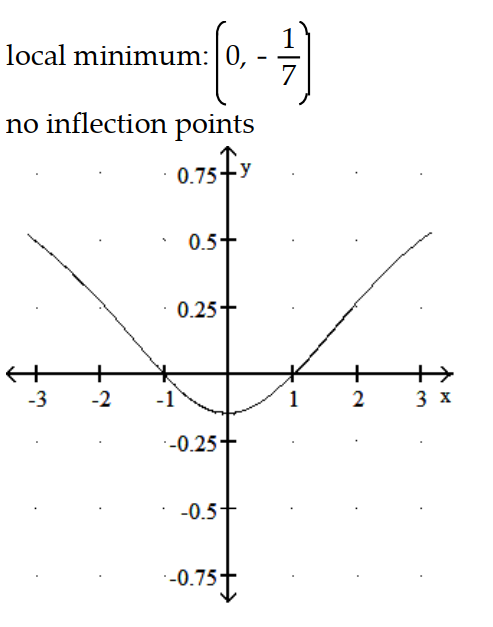
B)
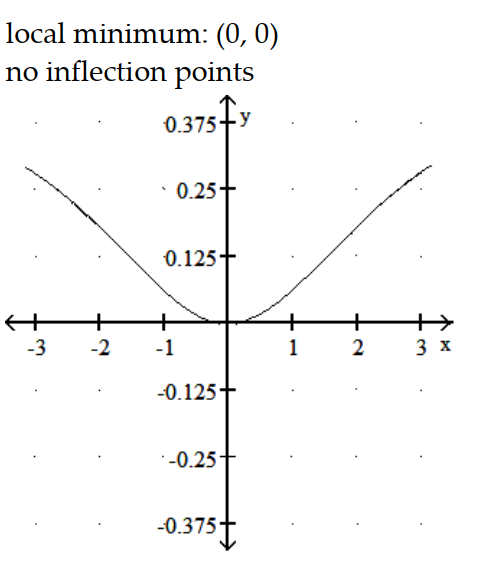
C)
D)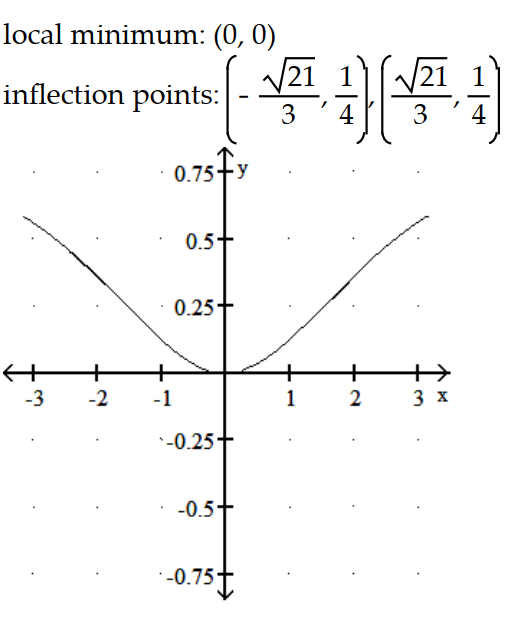
-y =
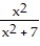

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
72
Graph the equation. Include the coordinates of any local extreme points and inflection points.
-y = x + cos 2x, 0 x
A)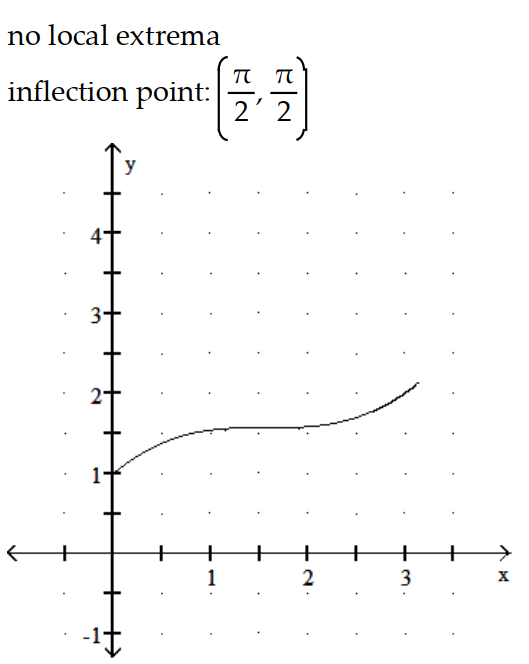
B)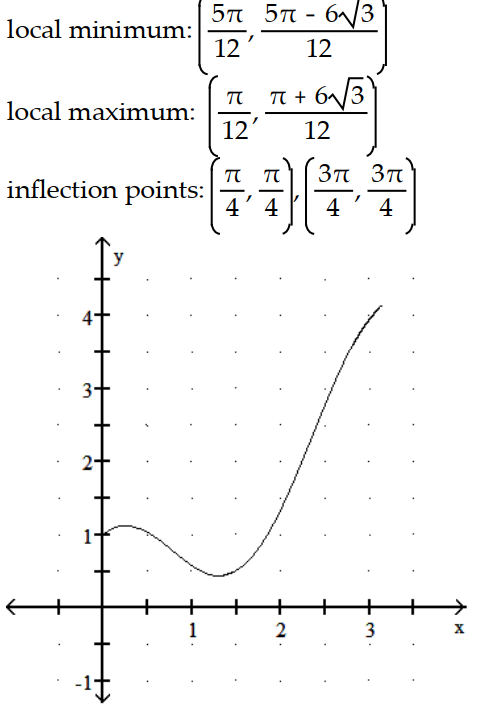
C)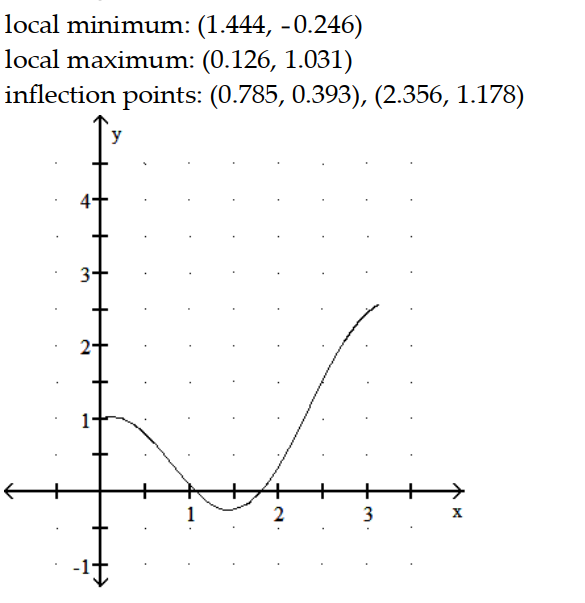
D)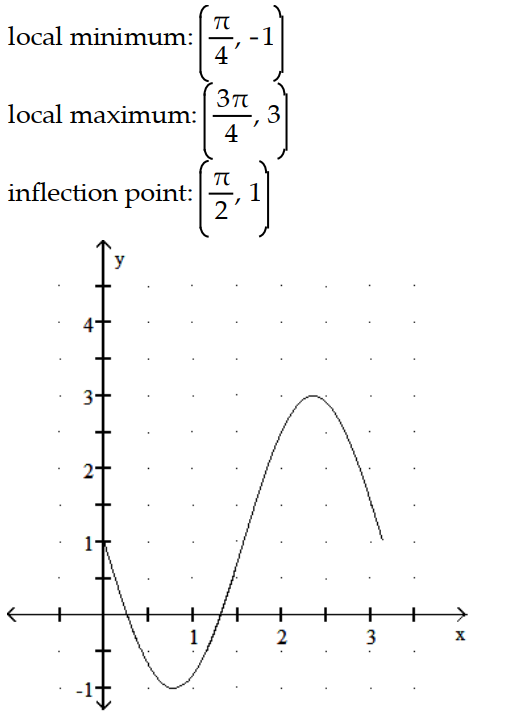
-y = x + cos 2x, 0 x

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
73
Graph the equation. Include the coordinates of any local extreme points and inflection points.
-y = x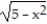
A)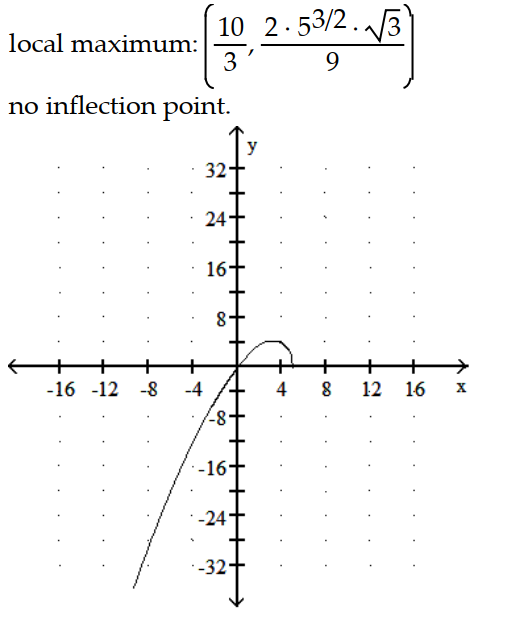
B)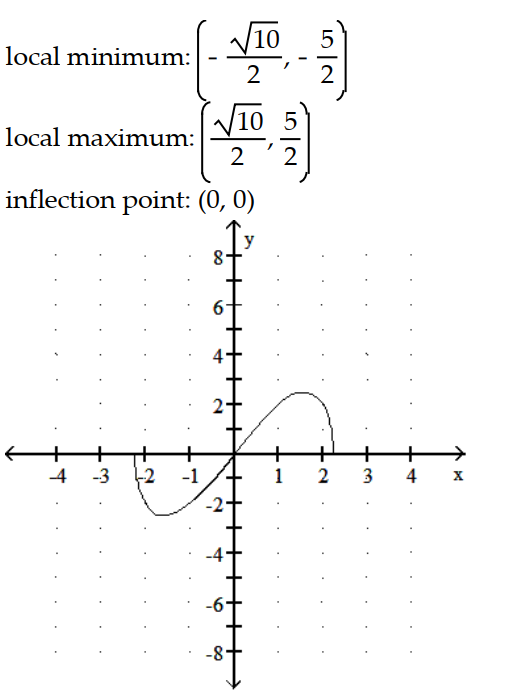
C)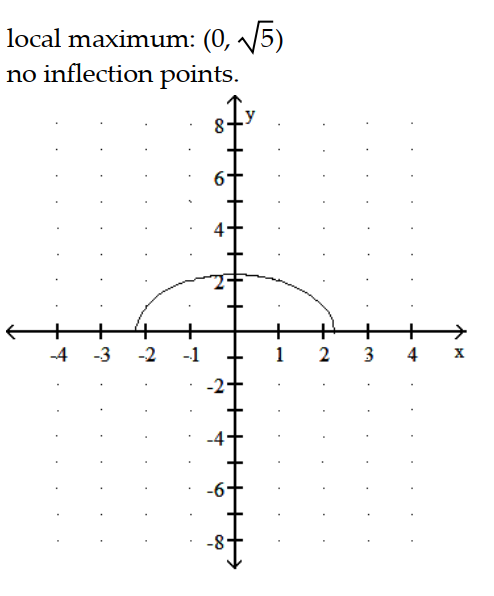
D)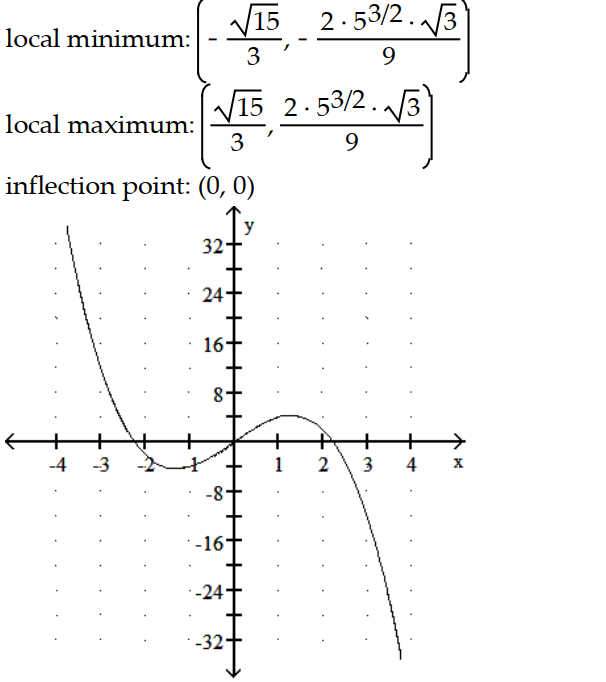
-y = x
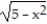

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
74
Sketch the graph and show all local extrema and inflection points.
-y = -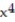 + 4
+ 4 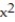 - 2
- 2
A)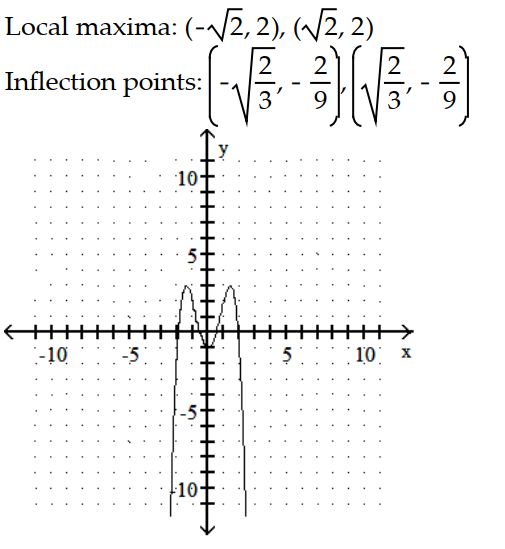
B)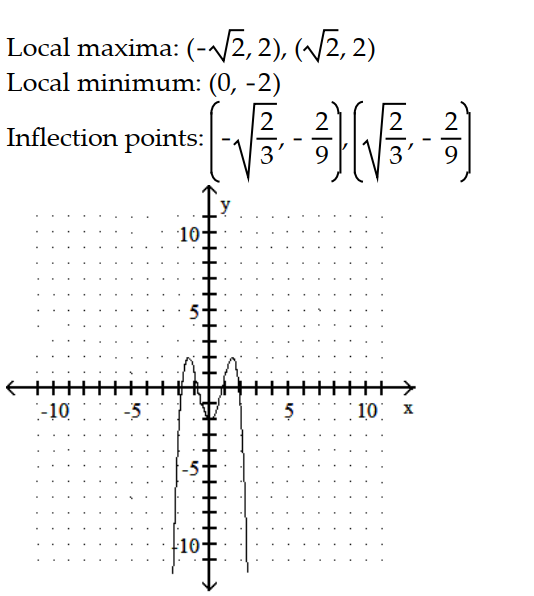
C)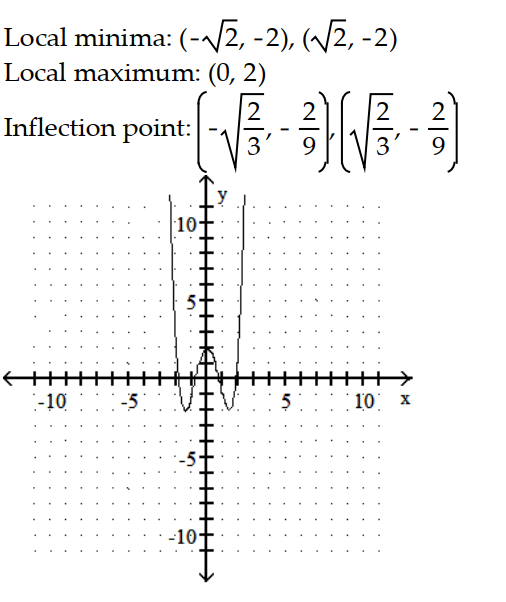
D)
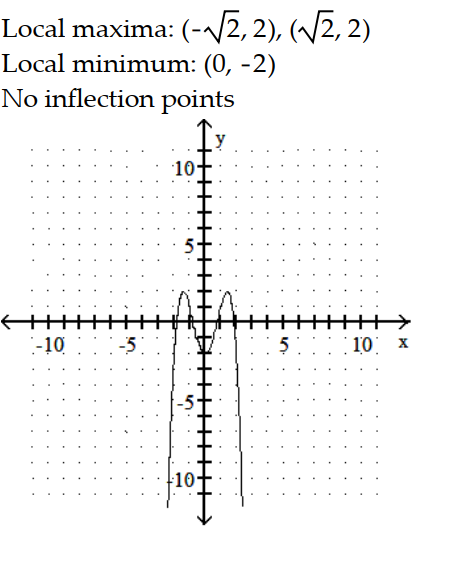
-y = -
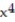 + 4
+ 4 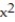 - 2
- 2
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
75
Sketch the graph and show all local extrema and inflection points.
-y = x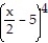
A)
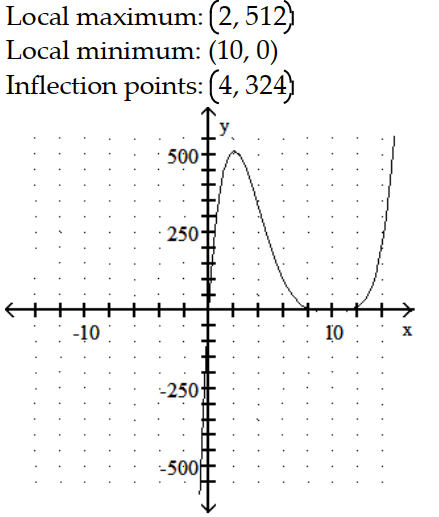
B)
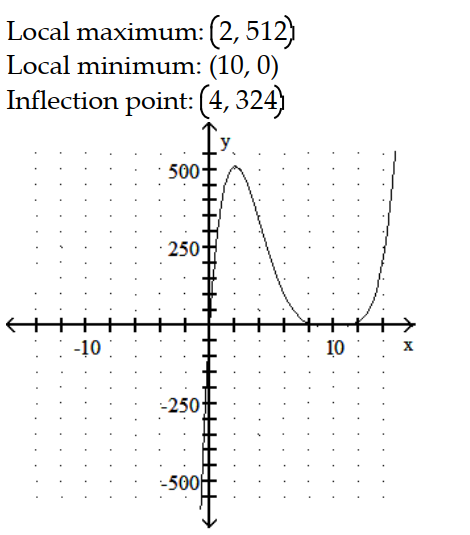
C)
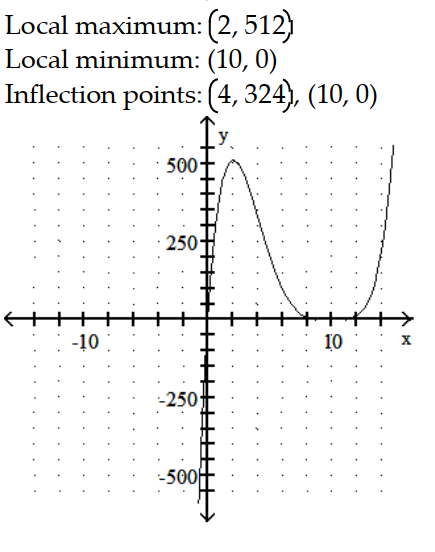
D)
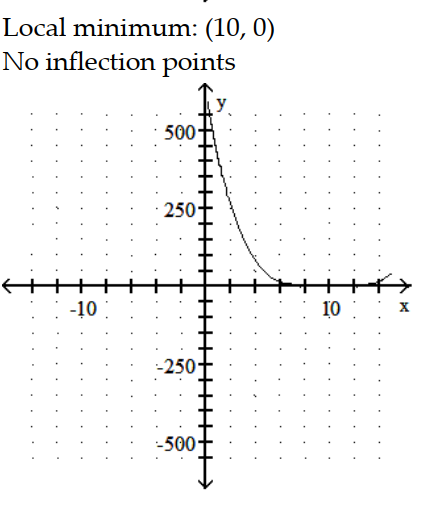
-y = x
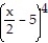

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
76
Sketch the graph and show all local extrema and inflection points.
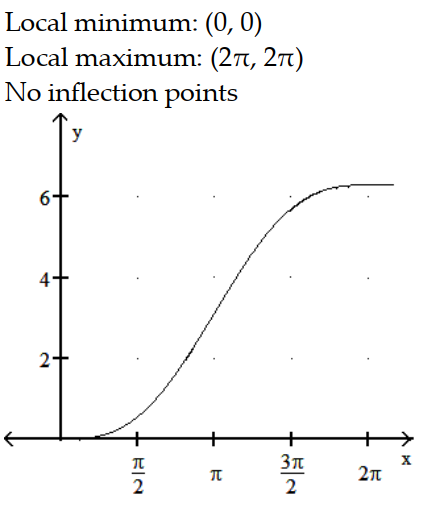
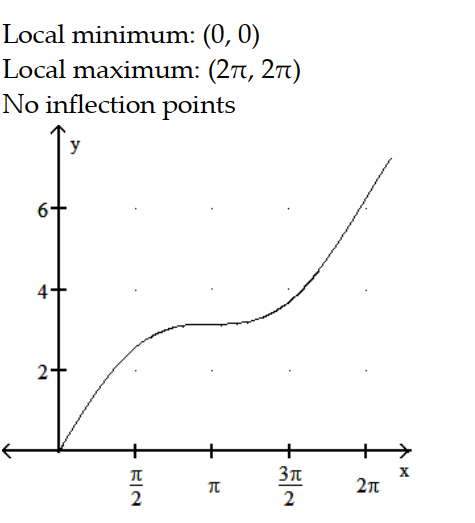
-y = x + sin x, 0 x 2

A)
B)
C)
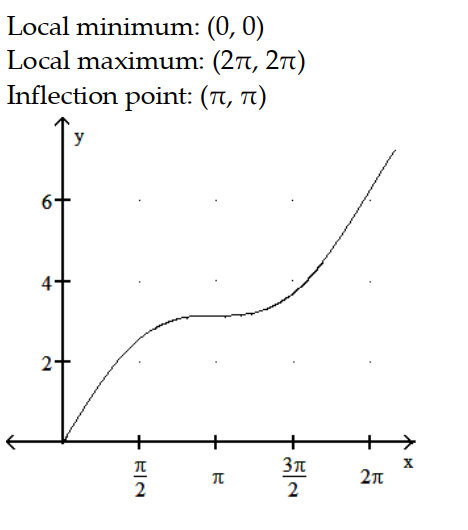
D)
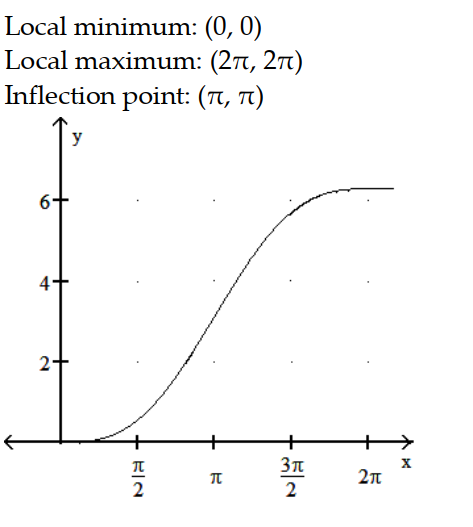
-y = x + sin x, 0 x 2

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
77
Sketch the graph and show all local extrema and inflection points.
-y = | - 4x|
- 4x|
A)
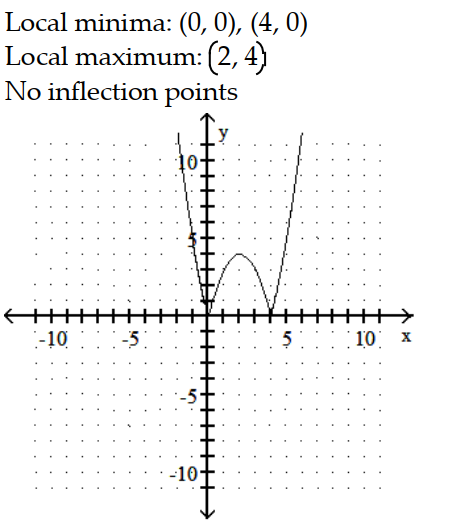
B)
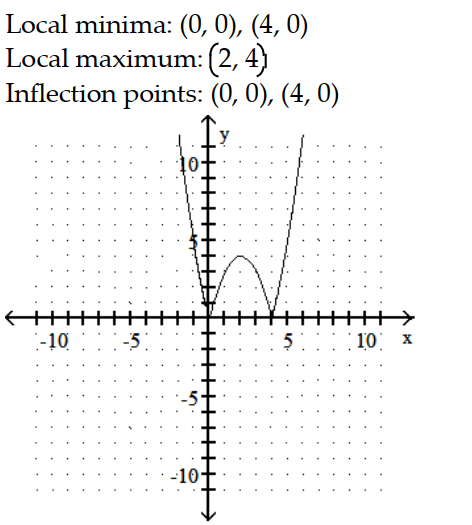
C)
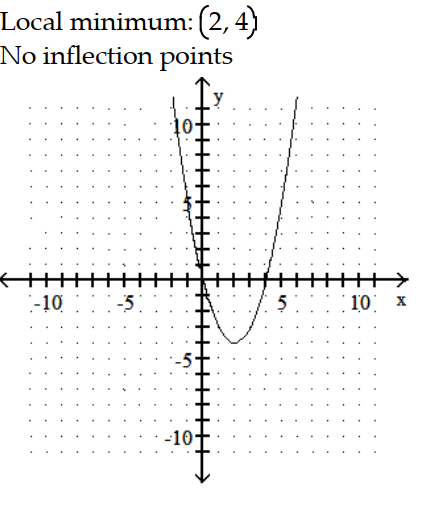
D)
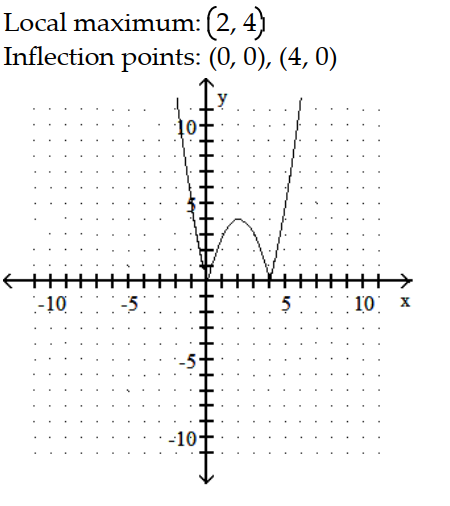
-y = |
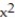 - 4x|
- 4x| 
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
78
Sketch the graph and show all local extrema and inflection points.
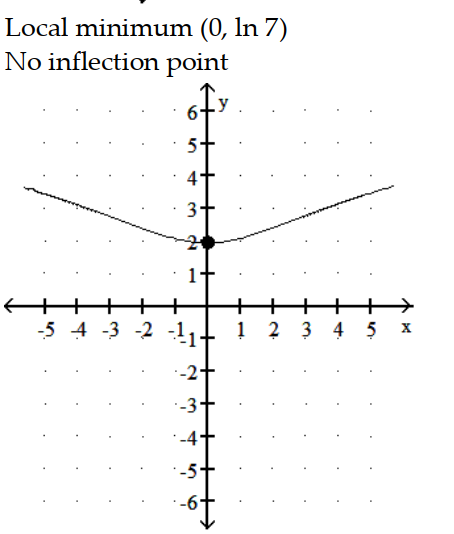
-y = ln ( 7 -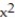 )
)
A)
B)
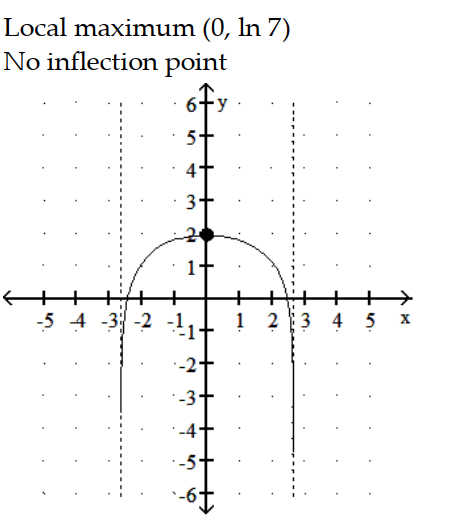
C)
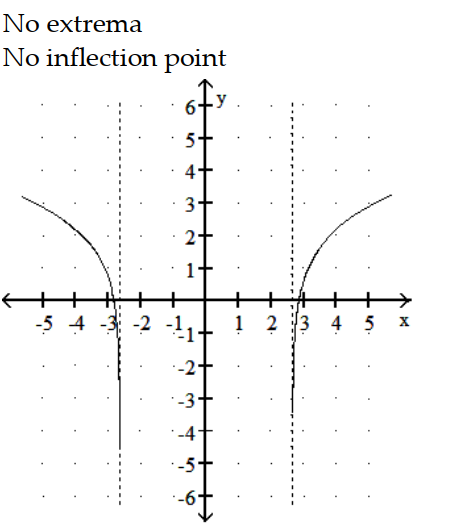
D)
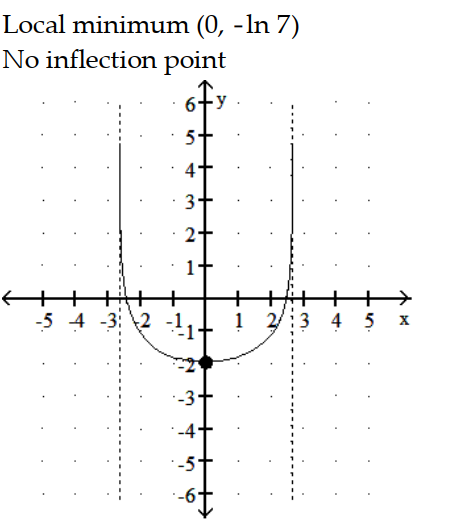
-y = ln ( 7 -
 )
) 
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
79
Sketch the graph and show all local extrema and inflection points.
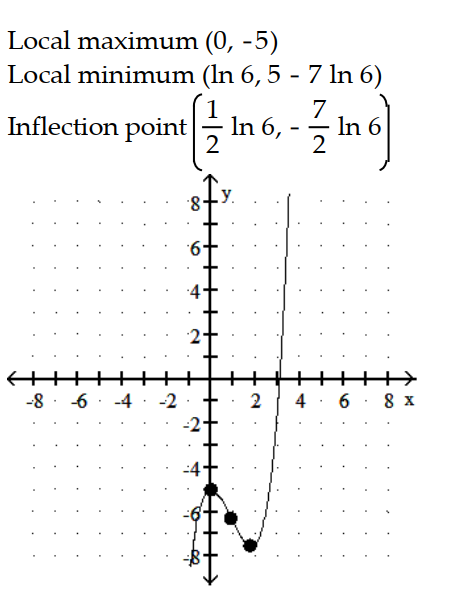
-y =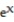 - 6
- 6 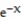 - 7x
- 7x
A)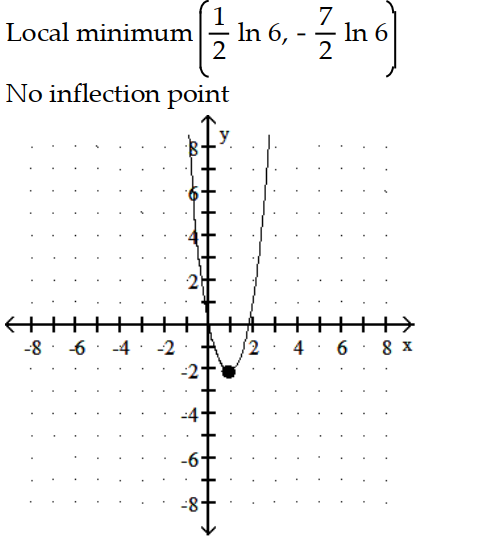
B)
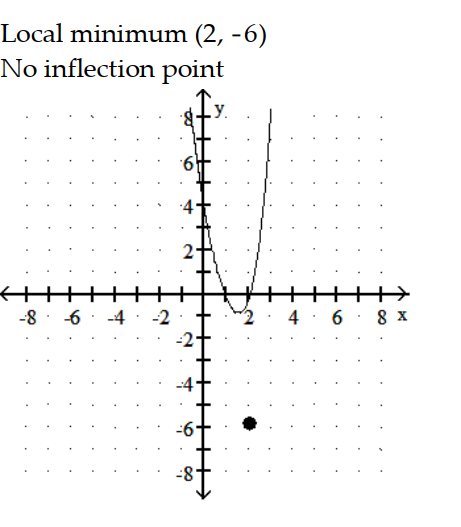
C)
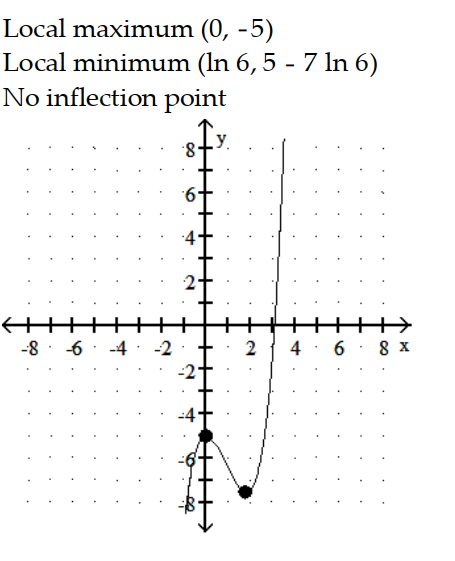
D)
-y =
 - 6
- 6 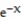 - 7x
- 7x 
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck
80
For the given expression 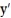 , find y'' and sketch the general shape of the graph of y = f(x).
, find y'' and sketch the general shape of the graph of y = f(x).
-y' =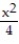 - 1
- 1
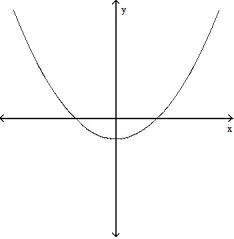
A)
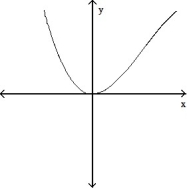
B)
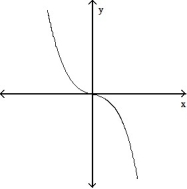
C)
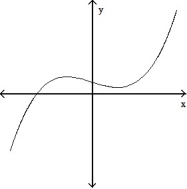
D)
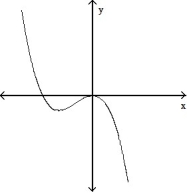
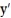 , find y'' and sketch the general shape of the graph of y = f(x).
, find y'' and sketch the general shape of the graph of y = f(x).-y' =
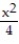 - 1
- 1
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 228 flashcards in this deck.
Unlock Deck
k this deck


