Exam 4: Applications of the Derivative
Exam 1: Functions226 Questions
Exam 2: Limits224 Questions
Exam 3: Derivatives367 Questions
Exam 4: Applications of the Derivative228 Questions
Exam 5: Integration166 Questions
Exam 6: Applications of Integration211 Questions
Exam 7: Logarithmic, Exponential, and Hyperbolic Functions85 Questions
Exam 8: Integration Techniques287 Questions
Exam 9: Differential Equations76 Questions
Exam 10: Sequences and Infinite Series173 Questions
Exam 11: Power Series103 Questions
Exam 12: Parametric and Polar Curves169 Questions
Exam 13: Vectors and the Geometry of Space131 Questions
Exam 14: Vector-Valued Functions83 Questions
Exam 15: Functions of Several Variables229 Questions
Exam 16: Multiple Integration299 Questions
Exam 17: Vector Calculus173 Questions
Select questions type
Solve the initial value problem.
-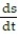 = cos t - sin t, s
= cos t - sin t, s 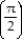 = 7
= 7
Free
(Multiple Choice)
4.8/5  (33)
(33)
Correct Answer:
D
Find all the roots of the function. Use preliminary analysis and graphing to determine good initial approximations. Round to six decimal places.
-f(x) = ln( 2x) - 2 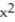 + 3x + 1
+ 3x + 1
Free
(Multiple Choice)
4.8/5  (38)
(38)
Correct Answer:
C
L'Hopital's rule does not help with the given limit. Find the limit some other way.
-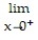
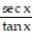
(Multiple Choice)
4.8/5  (35)
(35)
Use differentiation to determine whether the integral formula is correct.
-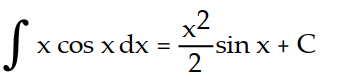
(True/False)
4.8/5  (41)
(41)
Determine whether the function satisfies the hypotheses of the Mean Value Theorem for the given interval.
-s(t) = 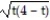 ,
, 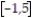
(True/False)
4.9/5  (33)
(33)
Solve the problem.
-You are driving along a highway at a steady 85 ft/sec when you see a deer ahead and slam on the brakes. What constant deceleration is required to stop your car in 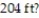
(Multiple Choice)
4.7/5  (43)
(43)
A fixed point of f is a value of x that satisfies the equation f(x) = x; it corresponds to a point at which the graph of f intersects the line y = x. Find all the fixed points of the function. Use preliminary analysis and graphing to determine good initial approximations. Round approximations to six decimal places.
-f(x) = 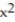 - 5
- 5
(Multiple Choice)
4.8/5  (36)
(36)
Find the largest open interval where the function is changing as requested.
-Decreasing f(x) = x3 - 4x
(Multiple Choice)
4.9/5  (40)
(40)
Use a calculator to compute the first 10 iterations of Newton's method when applied to the function with the given initial approximation. Make a table for the values. Round to six decimal places.
-f(x) = 3x - cos x; 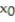 = 1
= 1
(Multiple Choice)
4.8/5  (33)
(33)
Express the relationship between a small change in x and the corresponding change in y in the form 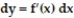 .
-y =
.
-y = 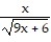
(Multiple Choice)
4.8/5  (35)
(35)
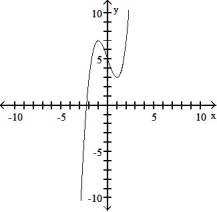
Use the graph of the function f(x) to locate the local extrema and identify the intervals where the function is concave up and concave down.
-
(Multiple Choice)
4.9/5  (32)
(32)
For the given expression 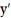 , find y'' and sketch the general shape of the graph of y = f(x).
-
, find y'' and sketch the general shape of the graph of y = f(x).
-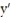 =
= 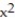 ( 1 - x)
( 1 - x)
(Multiple Choice)
4.7/5  (30)
(30)
Choose the one alternative that best completes the statement or answers the question.
-Determine the dimensions of the rectangle of largest area that can be inscribed in a semicircle of radius 3.
(Multiple Choice)
4.9/5  (43)
(43)
Find the absolute extreme values of the function on the interval.
-f(x) = tan x, - 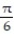 x
x 
(Multiple Choice)
5.0/5  (35)
(35)
Showing 1 - 20 of 228
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)