Deck 17: Vector Calculus
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/173
Play
Full screen (f)
Deck 17: Vector Calculus
1
Sketch the vector field in the plane along with its horizontal and vertical components at a representative assortment of points on the circle x2 + y2 = 4.
-F =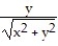 i -
i - 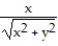 j
j
-F =
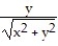 i -
i - 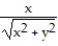 j
jAnswers will vary.
2
Sketch the vector field in the plane along with its horizontal and vertical components at a representative assortment of points on the circle x2 + y2 = 4.
-F =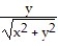 i +
i + 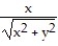 j
j
-F =
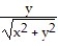 i +
i + 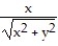 j
jAnswers will vary.
3
Sketch the vector field in the plane along with its horizontal and vertical components at a representative assortment of points on the circle x2 + y2 = 4.
-F = -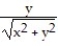 i -
i - 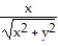 j
j
-F = -
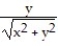 i -
i - 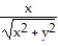 j
jAnswers will vary.
4
Sketch the vector field in the plane along with its horizontal and vertical components at a representative assortment of points on the circle x2 + y2 = 4.
-F = -xi - yj
-F = -xi - yj

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
5
Sketch the vector field in the plane along with its horizontal and vertical components at a representative assortment of points on the circle x2 + y2 = 4.
-F = -xi + yj
-F = -xi + yj

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
6
Sketch the vector field in the plane along with its horizontal and vertical components at a representative assortment of points on the circle x2 + y2 = 4.
-F = xi - yj
-F = xi - yj

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
7
Find the gradient field F of the function f.
-f(x, y, z) =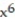
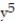 +
+ 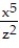
A)
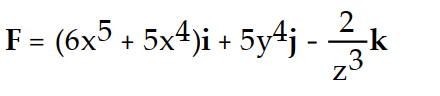
B)
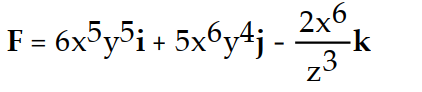
C)
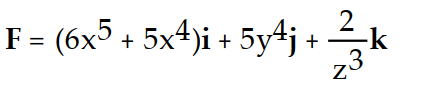
D)
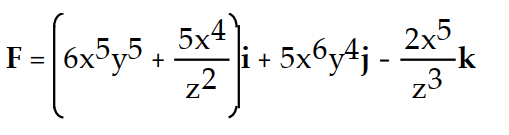
-f(x, y, z) =
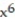
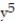 +
+ 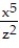
A)
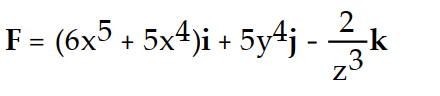
B)
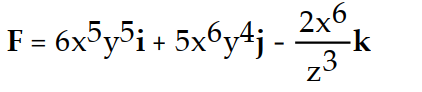
C)
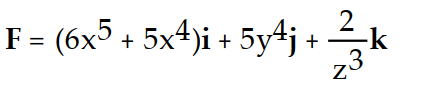
D)
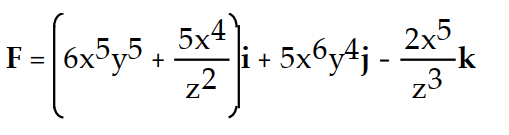

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
8
Find the gradient field F of the function f.
-f(x, y, z) =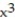
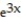 +
+ 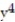
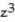
A)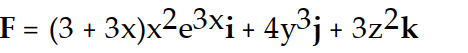
B)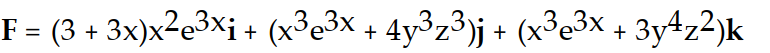
C)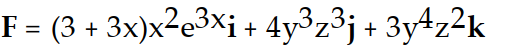
D)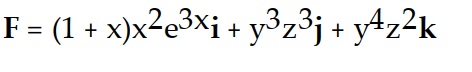
-f(x, y, z) =
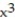
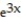 +
+ 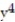
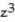
A)
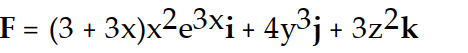
B)
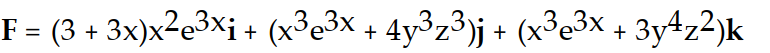
C)
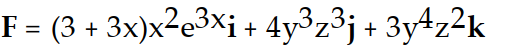
D)
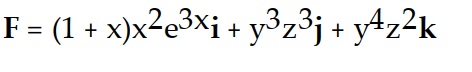

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
9
Find the gradient field F of the function f.
-f(x, y, z) =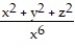
A)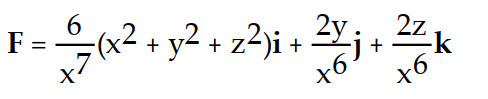
B)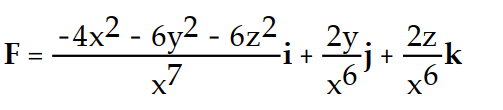
C)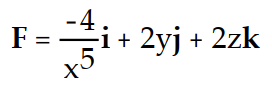
D)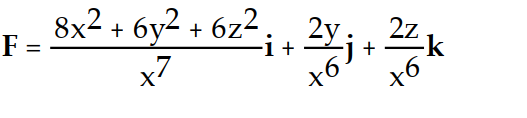
-f(x, y, z) =
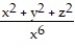
A)
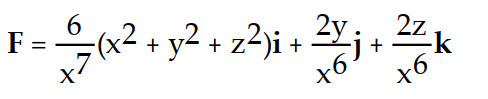
B)
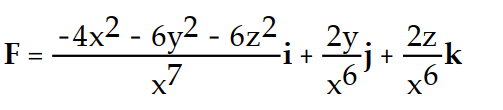
C)
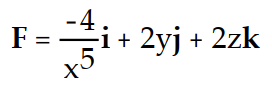
D)
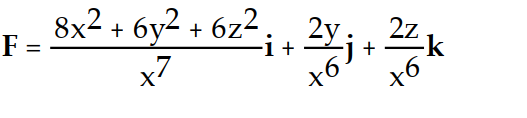

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
10
Find the gradient field F of the function f.
-f(x, y, z) = ln (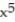 +
+ 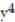 +
+ 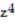 )
)
A)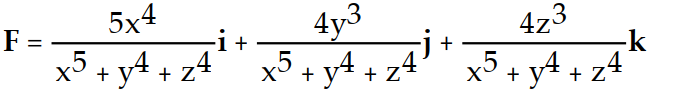
B)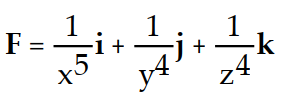
C)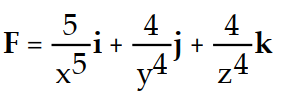
D)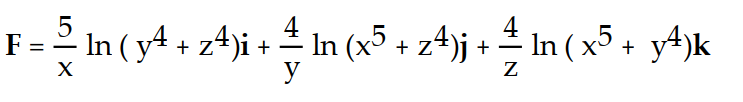
-f(x, y, z) = ln (
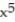 +
+ 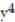 +
+ 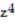 )
)A)
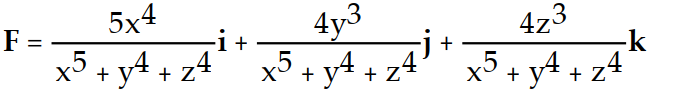
B)
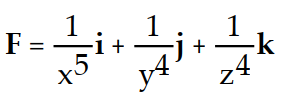
C)
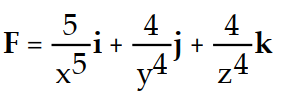
D)
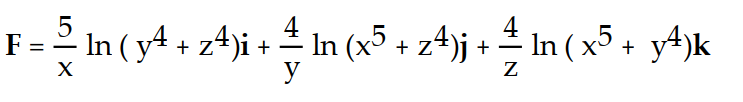

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
11
Find the gradient field F of the function f.
-f(x, y, z) =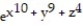
A)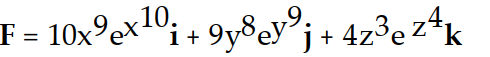
B)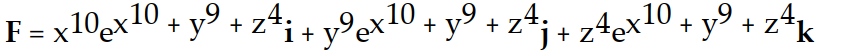
C)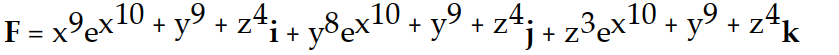
D)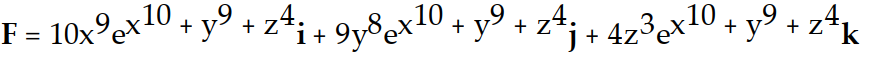
-f(x, y, z) =
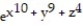
A)
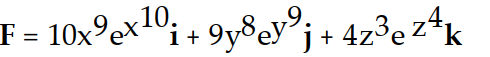
B)
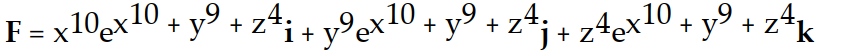
C)
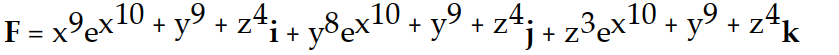
D)
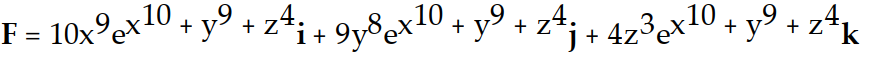

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
12
Find the gradient field F of the function f.
-f(x, y, z) = z sin (x + y + z)
A)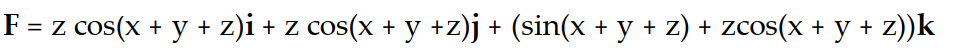
B)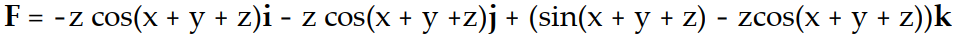
C)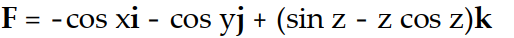
D)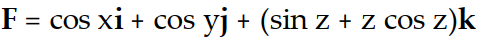
-f(x, y, z) = z sin (x + y + z)
A)
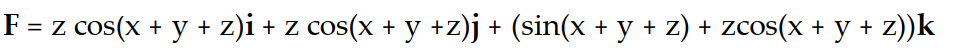
B)
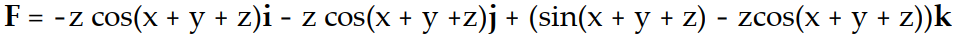
C)
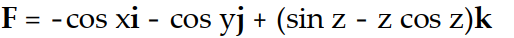
D)
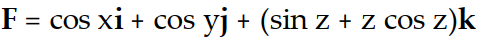

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
13
Find the gradient field F of the function f.
-f(x, y, z) =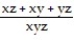
A)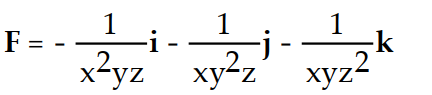
B)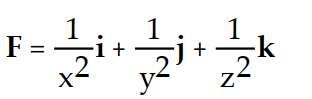
C)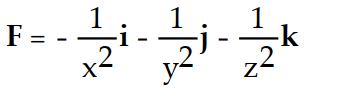
D)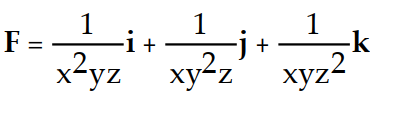
-f(x, y, z) =
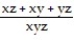
A)
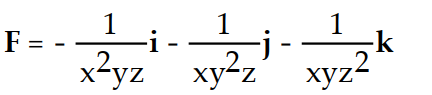
B)
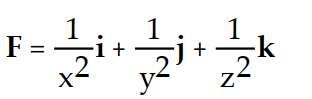
C)
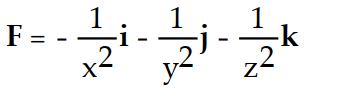
D)
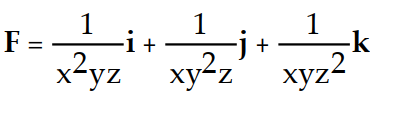

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
14
Find the gradient field F of the function f.
-f(x, y, z) = (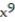
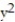 -
- 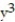
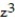 )
) 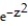
A)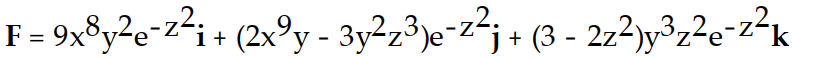
B)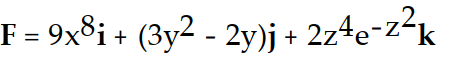
C)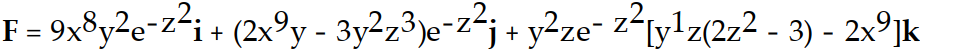
D)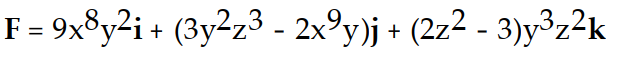
-f(x, y, z) = (
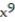
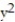 -
- 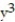
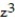 )
) 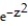
A)
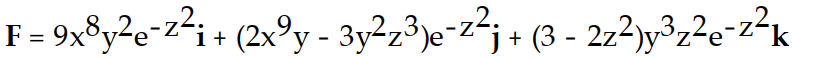
B)
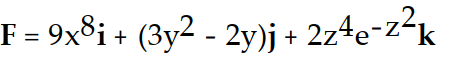
C)
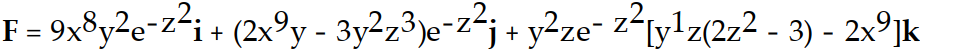
D)
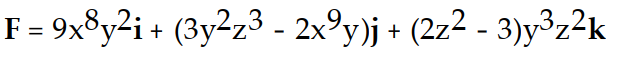

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
15
Find the gradient field F of the function f.
-f(x, y, z) = ln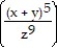 +
+ 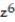
A)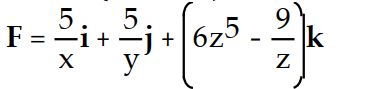
B)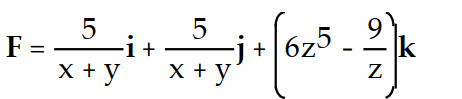
C)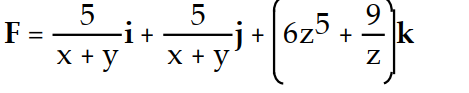
D)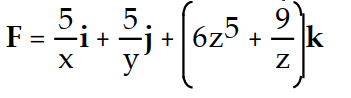
-f(x, y, z) = ln
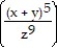 +
+ 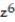
A)
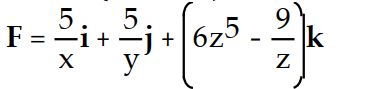
B)
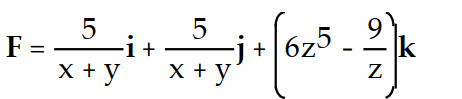
C)
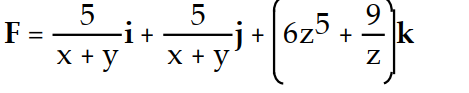
D)
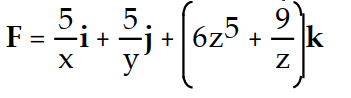

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
16
Find the gradient field F of the function f.
-f(x, y, z) =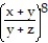
A)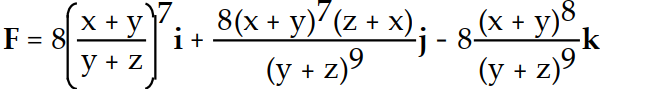
B)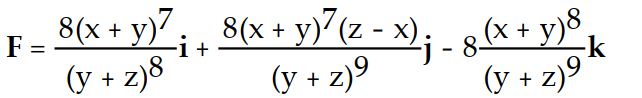
C)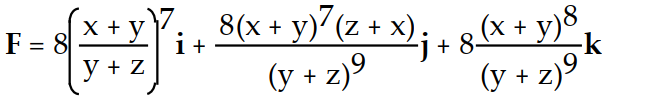
D)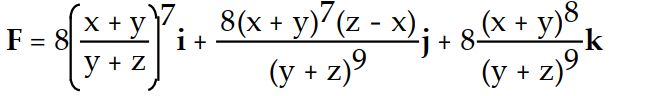
-f(x, y, z) =
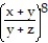
A)
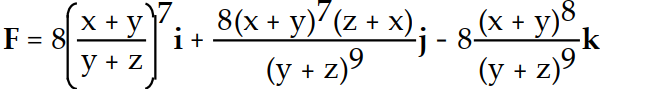
B)
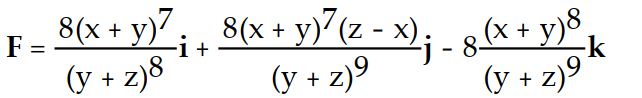
C)
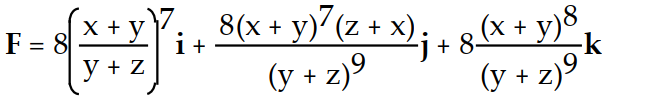
D)
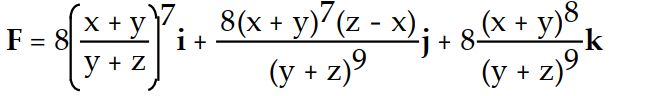

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
17
Evaluate the line integral of f(x,y) along the curve C.
-f(x, y) =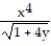 , C: y =
, C: y = 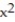 , 0 x 1
, 0 x 1
A) 1/4
B) 1/5
C) 0
D) 1
-f(x, y) =
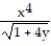 , C: y =
, C: y = 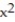 , 0 x 1
, 0 x 1A) 1/4
B) 1/5
C) 0
D) 1

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
18
Evaluate the line integral of f(x,y) along the curve C.
-f(x, y) =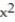 +
+ 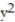 , C: y = -2x - 4, 0 x 3
, C: y = -2x - 4, 0 x 3
A) 55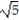
B) 165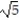
C) 255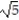
D) 165
-f(x, y) =
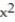 +
+ 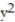 , C: y = -2x - 4, 0 x 3
, C: y = -2x - 4, 0 x 3A) 55
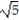
B) 165
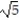
C) 255
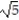
D) 165

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
19
Evaluate the line integral of f(x,y) along the curve C.
-f(x, y) = y + x, C: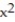 +
+ 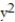 = 4 in the first quadrant from ( 2, 0) to (0, 2)
= 4 in the first quadrant from ( 2, 0) to (0, 2)
A) 16
B) 8
C) 0
D) 4
-f(x, y) = y + x, C:
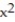 +
+ 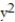 = 4 in the first quadrant from ( 2, 0) to (0, 2)
= 4 in the first quadrant from ( 2, 0) to (0, 2)A) 16
B) 8
C) 0
D) 4

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
20
Evaluate the line integral of f(x,y) along the curve C.
-f(x, y) =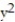 +
+ 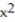 , C: the perimeter of the circle
, C: the perimeter of the circle 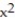 +
+ 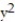 = 16
= 16
A) 8
B) 32
C) 128
D) 64
-f(x, y) =
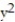 +
+ 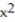 , C: the perimeter of the circle
, C: the perimeter of the circle 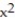 +
+ 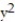 = 16
= 16A) 8
B) 32
C) 128
D) 64

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
21
Evaluate the line integral of f(x,y) along the curve C.
-f(x, y) = x, C: y =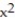 , 0 x
, 0 x 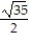
A) 215/12
B) 215
C) 215/8
D) 215/3
-f(x, y) = x, C: y =
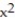 , 0 x
, 0 x 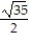
A) 215/12
B) 215
C) 215/8
D) 215/3

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
22
Evaluate the line integral of f(x,y) along the curve C.
-f(x, y) = cos x + sin y, C: y = x, 0 x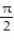
A)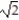
B) 2
C) 0
D) 2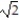
-f(x, y) = cos x + sin y, C: y = x, 0 x
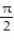
A)
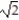
B) 2
C) 0
D) 2

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
23
Evaluate the line integral of f(x,y) along the curve C.
-f(x,y) = 3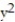 , C: y =
, C: y = 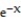 , 0 x 3
, 0 x 3
A)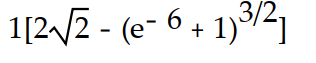
B)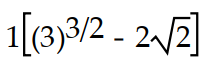
C)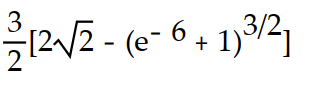
D)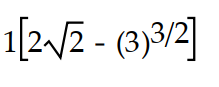
-f(x,y) = 3
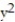 , C: y =
, C: y = 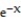 , 0 x 3
, 0 x 3A)
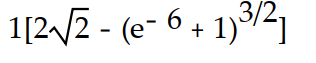
B)
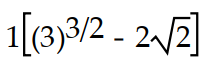
C)
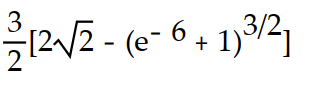
D)
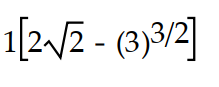

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
24
Evaluate the line integral along the curve C.
-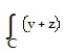 ds , C is the straight-line segment x = 0, y = 3 - t, z = t from (0, 3, 0) to
ds , C is the straight-line segment x = 0, y = 3 - t, z = t from (0, 3, 0) to 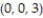
A) 9
B) 9/2
C) 0
D) 9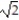
-
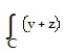 ds , C is the straight-line segment x = 0, y = 3 - t, z = t from (0, 3, 0) to
ds , C is the straight-line segment x = 0, y = 3 - t, z = t from (0, 3, 0) to 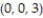
A) 9
B) 9/2
C) 0
D) 9

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
25
Evaluate the line integral along the curve C.
-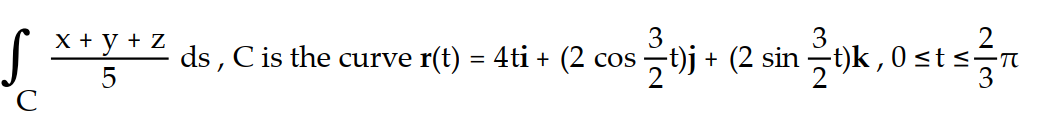
A)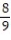
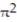 +
+ 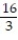
B)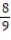
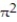 +
+ 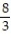
C)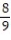 +
+ 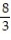
D)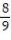
-
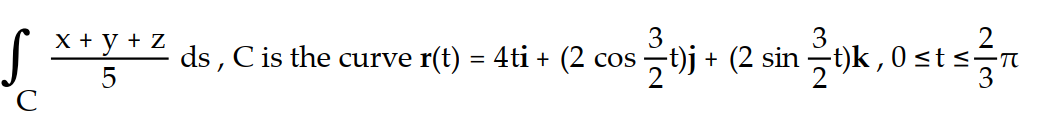
A)
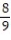
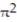 +
+ 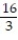
B)
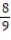
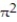 +
+ 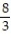
C)
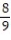 +
+ 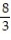
D)
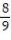

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
26
Evaluate the line integral along the curve C.
-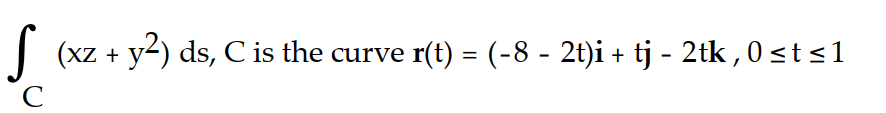
A) - 19/3
B) -19
C) 29
D) 29/3
-
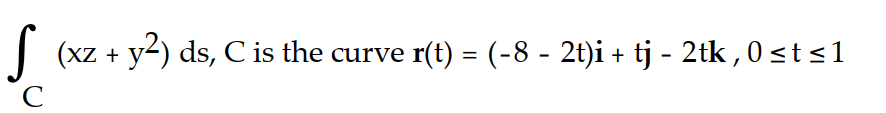
A) - 19/3
B) -19
C) 29
D) 29/3

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
27
Evaluate the line integral along the curve C.
-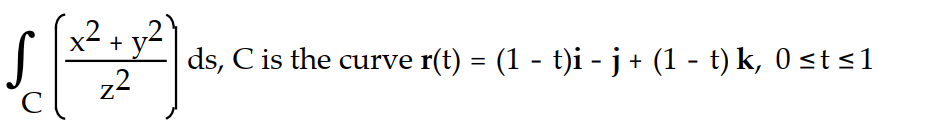
A) 1/0
B) 5/0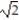
C) 1/0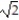
D) 2/0
-
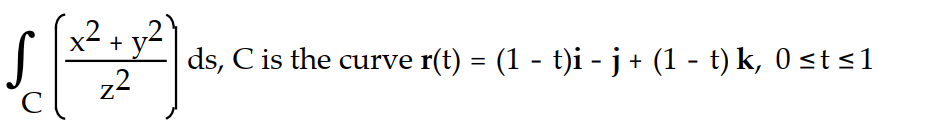
A) 1/0
B) 5/0
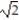
C) 1/0
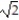
D) 2/0

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
28
Evaluate the line integral along the curve C.
-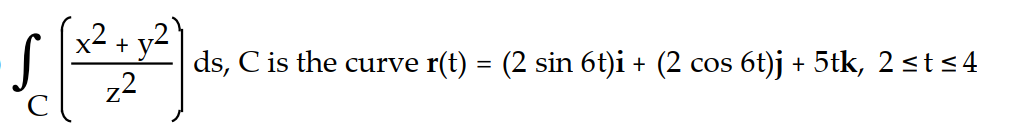
A) 13/25
B) 1/25
C) 169/25
D) - 91/400
-
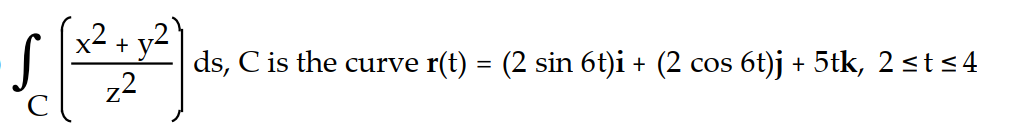
A) 13/25
B) 1/25
C) 169/25
D) - 91/400

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
29
Evaluate the line integral along the curve C.
-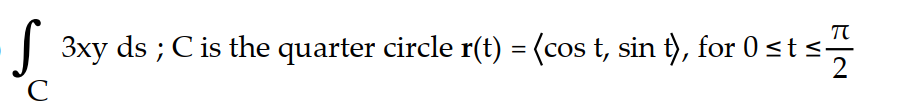
A) 3/2
B) 3
C)
D) 0
-
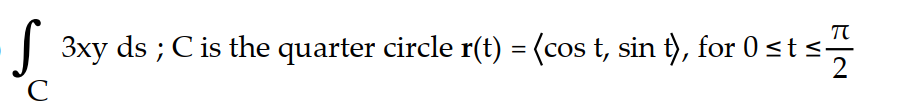
A) 3/2
B) 3
C)
D) 0

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
30
Evaluate the line integral along the curve C.
-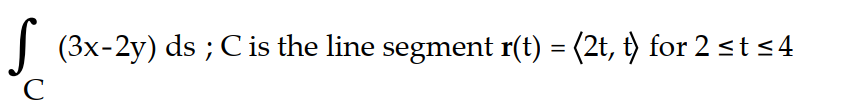
A) 48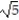
B) 24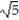
C)48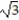
D) 24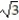
-
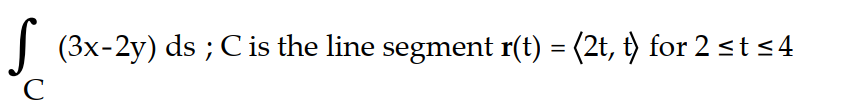
A) 48
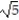
B) 24
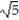
C)48
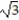
D) 24

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
31
Find the work done by F over the curve in the direction of increasing t.
-F = 10zi + 2xj + 9yk; C: r(t) = ti + tj + tk, 0 t 1
A) W = 42
B) W = 21/2
C) W = 7
D) W = 21
-F = 10zi + 2xj + 9yk; C: r(t) = ti + tj + tk, 0 t 1
A) W = 42
B) W = 21/2
C) W = 7
D) W = 21

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
32
Find the work done by F over the curve in the direction of increasing t.
-F = -8yi + 8xj + 3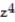 k; C: r(t) = cos ti + sin tj, 0 t 6
k; C: r(t) = cos ti + sin tj, 0 t 6
A) W = 96
B) W = 0
C) W = 48
D) W = 144
-F = -8yi + 8xj + 3
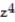 k; C: r(t) = cos ti + sin tj, 0 t 6
k; C: r(t) = cos ti + sin tj, 0 t 6A) W = 96
B) W = 0
C) W = 48
D) W = 144

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
33
Find the work done by F over the curve in the direction of increasing t.
-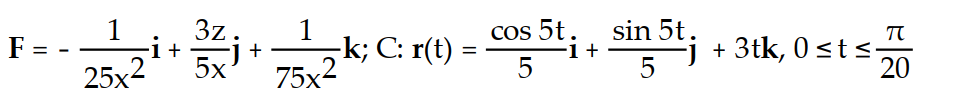
A)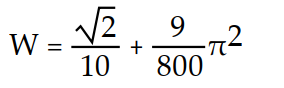
B)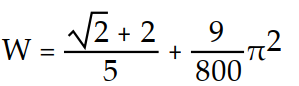
C)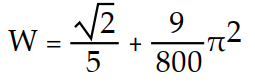
D)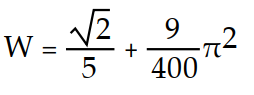
-
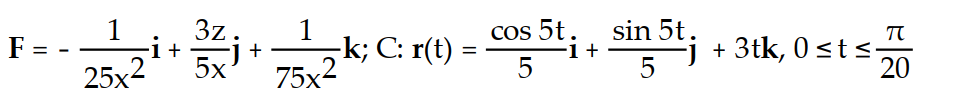
A)
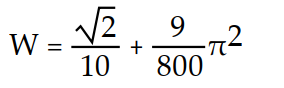
B)
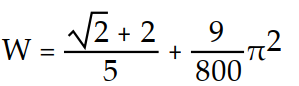
C)
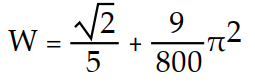
D)
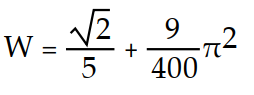

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
34
Find the work done by F over the curve in the direction of increasing t.
-F = xyi + 8j + 3xk; C: r(t) = cos 8ti + sin 8tj + tk, 0 t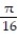
A) W = 0
B) W = 25/3
C) W = 209/24
D) W = 193/24
-F = xyi + 8j + 3xk; C: r(t) = cos 8ti + sin 8tj + tk, 0 t
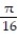
A) W = 0
B) W = 25/3
C) W = 209/24
D) W = 193/24

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
35
Find the work done by F over the curve in the direction of increasing t.
-F = 5yi +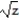 j + ( 5x + 2z)k; C: r(t) = ti +
j + ( 5x + 2z)k; C: r(t) = ti + 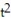 j + tk, 0 t 2
j + tk, 0 t 2
A) W = 47 + 20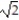
B) W =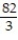 +
+ 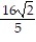
C) W =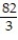 + 20
+ 20 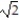
D) W = 0
-F = 5yi +
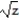 j + ( 5x + 2z)k; C: r(t) = ti +
j + ( 5x + 2z)k; C: r(t) = ti + 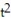 j + tk, 0 t 2
j + tk, 0 t 2A) W = 47 + 20
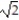
B) W =
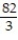 +
+ 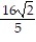
C) W =
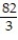 + 20
+ 20 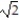
D) W = 0

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
36
Calculate the circulation of the field F around the closed curve C.
-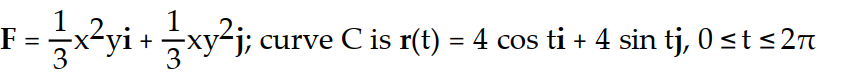
A) 2/3
B) 4/3
C) 8/3
D) 0
-
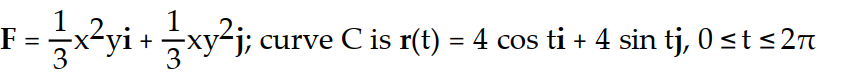
A) 2/3
B) 4/3
C) 8/3
D) 0

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
37
Calculate the circulation of the field F around the closed curve C.
-F = xyi + 5j , curve C is r(t) = 3 cos ti + 3 sin tj, 0 t 2
A) 16
B) 4
C) 10
D) 0
-F = xyi + 5j , curve C is r(t) = 3 cos ti + 3 sin tj, 0 t 2
A) 16
B) 4
C) 10
D) 0

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
38
Calculate the circulation of the field F around the closed curve C.
-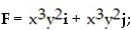 curve C is the counterclockwise path around the rectangle with vertices at
curve C is the counterclockwise path around the rectangle with vertices at 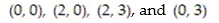
A) 0
B) 72
C) 108
D) 36
-
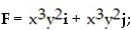 curve C is the counterclockwise path around the rectangle with vertices at
curve C is the counterclockwise path around the rectangle with vertices at 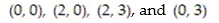
A) 0
B) 72
C) 108
D) 36

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
39
Calculate the circulation of the field F around the closed curve C.
-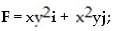 curve C is the counterclockwise path around
curve C is the counterclockwise path around 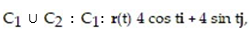
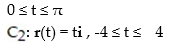
A) 32
B) 16
C) 0
D) 4
-
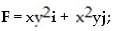 curve C is the counterclockwise path around
curve C is the counterclockwise path around 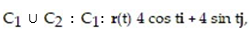
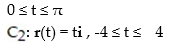
A) 32
B) 16
C) 0
D) 4

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
40
Calculate the circulation of the field F around the closed curve C.
-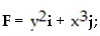 curve C is the counterclockwise path around the triangle with vertices at (0,0) , (2,.) and (0,4)
curve C is the counterclockwise path around the triangle with vertices at (0,0) , (2,.) and (0,4)
A) 8/3
B) 56/3
C) - 8/3
D) 0
-
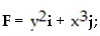 curve C is the counterclockwise path around the triangle with vertices at (0,0) , (2,.) and (0,4)
curve C is the counterclockwise path around the triangle with vertices at (0,0) , (2,.) and (0,4) A) 8/3
B) 56/3
C) - 8/3
D) 0

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
41
Calculate the circulation of the field F around the closed curve C.
-F = (-x - y)i + (x + y)j , curve C is the counterclockwise path around the circle with radius 2 centered at (2,1)
A) 16
B) 8(1 + ) + 24
C) 8(1 + )
D) 8
-F = (-x - y)i + (x + y)j , curve C is the counterclockwise path around the circle with radius 2 centered at (2,1)
A) 16
B) 8(1 + ) + 24
C) 8(1 + )
D) 8

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
42
Calculate the flux of the field F across the closed plane curve C.
-F = xi + yj; the curve C is the counterclockwise path around the circle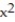 +
+ 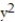 = 16
= 16
A) 64
B) 8
C) 0
D) 32
-F = xi + yj; the curve C is the counterclockwise path around the circle
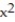 +
+ 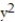 = 16
= 16A) 64
B) 8
C) 0
D) 32

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
43
Calculate the flux of the field F across the closed plane curve C.
-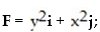 the curve C is the closed counterclockwise path formed from the semicircle
the curve C is the closed counterclockwise path formed from the semicircle  0 ≤ t ≤ π, and the straight line segment from (-4, 0) to ( 4, 0)
0 ≤ t ≤ π, and the straight line segment from (-4, 0) to ( 4, 0)
A) 64/3
B) - 32/3
C) 0
D) 32/3
-
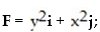 the curve C is the closed counterclockwise path formed from the semicircle
the curve C is the closed counterclockwise path formed from the semicircle  0 ≤ t ≤ π, and the straight line segment from (-4, 0) to ( 4, 0)
0 ≤ t ≤ π, and the straight line segment from (-4, 0) to ( 4, 0) A) 64/3
B) - 32/3
C) 0
D) 32/3

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
44
Calculate the flux of the field F across the closed plane curve C.
-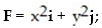 the curve C is the closed counterclockwise path around the triangle with vertices at
the curve C is the closed counterclockwise path around the triangle with vertices at 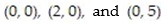
A) 70
B) 70/3
C) -10
D) 0
-
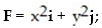 the curve C is the closed counterclockwise path around the triangle with vertices at
the curve C is the closed counterclockwise path around the triangle with vertices at 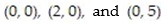
A) 70
B) 70/3
C) -10
D) 0

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
45
Calculate the flux of the field F across the closed plane curve C.
-F = xi + yj; the curve C is the closed counterclockwise path around the rectangle with vertices at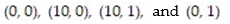
A) 101
B) 20
C) 0
D) 99
-F = xi + yj; the curve C is the closed counterclockwise path around the rectangle with vertices at
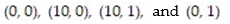
A) 101
B) 20
C) 0
D) 99

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
46
Calculate the flux of the field F across the closed plane curve C.
-F = (x+y)i + xyj; the curve C is the closed counterclockwise path around the rectangle with vertices at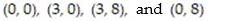
A) 52
B) 60
C) 96
D) 124
-F = (x+y)i + xyj; the curve C is the closed counterclockwise path around the rectangle with vertices at
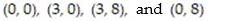
A) 52
B) 60
C) 96
D) 124

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
47
Calculate the flux of the field F across the closed plane curve C.
-F = yi - xj; the curve C is the circle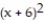 +
+ 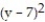 = 36
= 36
A) -144
B) -72
C) 0
D) 72
-F = yi - xj; the curve C is the circle
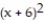 +
+ 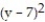 = 36
= 36A) -144
B) -72
C) 0
D) 72

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
48
Calculate the flux of the field F across the closed plane curve C.
-F = xi + yj; the curve C is the circle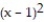 +
+ 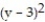 = 121
= 121
A) 242 + 11
B) 242
C) 0
D) 2
-F = xi + yj; the curve C is the circle
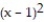 +
+ 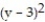 = 121
= 121A) 242 + 11
B) 242
C) 0
D) 2

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
49
Find the mass of the wire that lies along the curve r and has density ?.
-r(t) =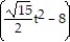 i + 7tj, 0 t 1;
i + 7tj, 0 t 1; 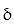 = 3t
= 3t
A) 169/15 units
B) 57 units
C) 169/10 units
D) 3/2 units
-r(t) =
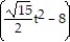 i + 7tj, 0 t 1;
i + 7tj, 0 t 1; 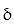 = 3t
= 3tA) 169/15 units
B) 57 units
C) 169/10 units
D) 3/2 units

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
50
Find the mass of the wire that lies along the curve r and has density ?.
-r(t) = 7i + ( 9 - 4t)j + 3tk, 0 t 2 ;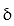 = 5(1 + sin 7t)
= 5(1 + sin 7t)
A) 10 units
B) 50/7 + 50 units
C) 50 units
D) 100/7 + 50 units
-r(t) = 7i + ( 9 - 4t)j + 3tk, 0 t 2 ;
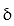 = 5(1 + sin 7t)
= 5(1 + sin 7t)A) 10 units
B) 50/7 + 50 units
C) 50 units
D) 100/7 + 50 units

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
51
Find the mass of the wire that lies along the curve r and has density ?.
-r(t) = ( 7 cos t)i + ( 7 sin t)j + 7tk, 0 t 2 ;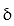 = 8
= 8
A) 112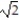 units
units
B) 16 units
C) 784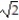 units
units
D) 14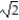 units
units
-r(t) = ( 7 cos t)i + ( 7 sin t)j + 7tk, 0 t 2 ;
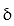 = 8
= 8A) 112
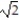 units
unitsB) 16 units
C) 784
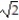 units
unitsD) 14
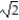 units
units
Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
52
Find the mass of the wire that lies along the curve r and has density ?.
-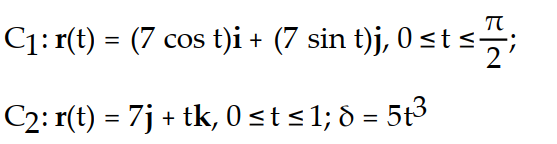
A)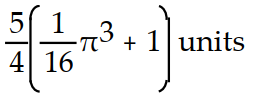
B)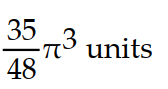
C)
D)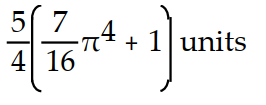
-
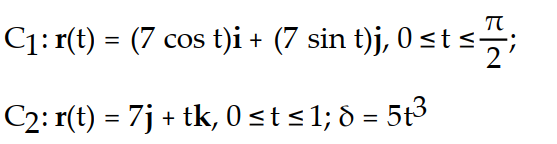
A)
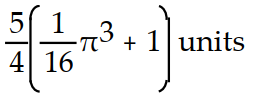
B)
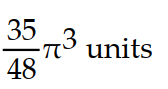
C)
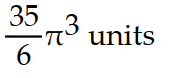
D)
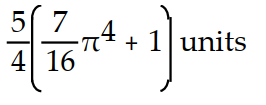

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
53
Find the potential function f for the field F.
-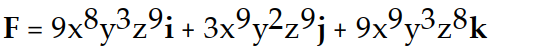
A)
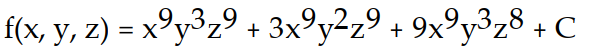
B)
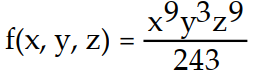
C)
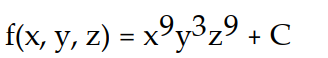
D)
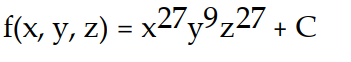
-
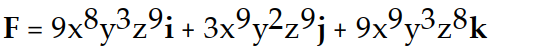
A)
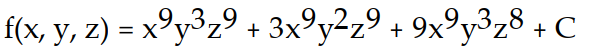
B)
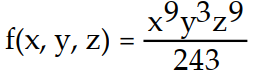
C)
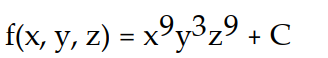
D)
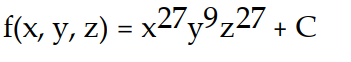

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
54
Find the potential function f for the field F.
-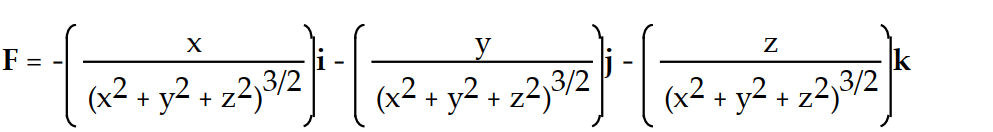
A)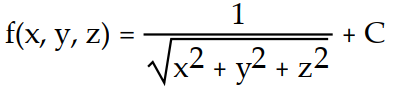
B)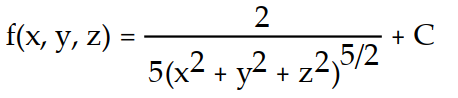
C)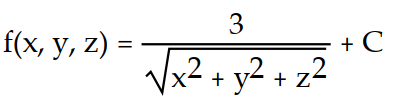
D)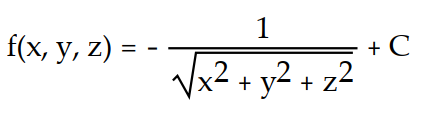
-
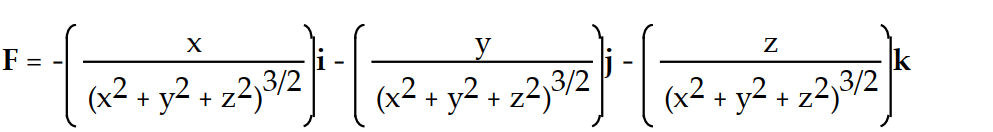
A)
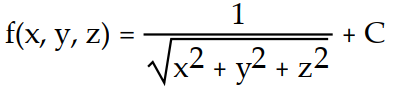
B)
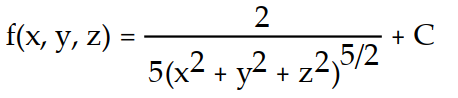
C)
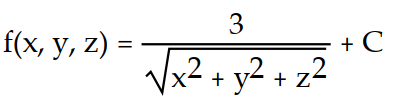
D)
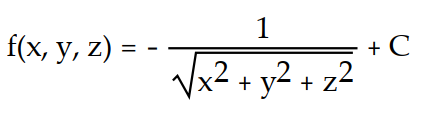

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
55
Find the potential function f for the field F.
-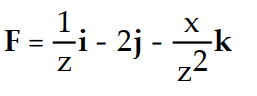
A)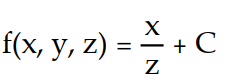
B)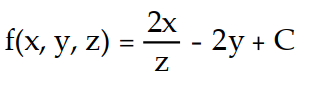
C)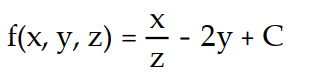
D)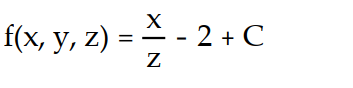
-
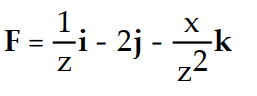
A)
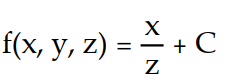
B)
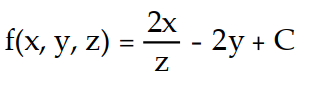
C)
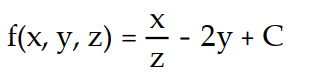
D)
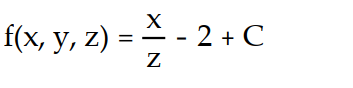

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
56
Find the potential function f for the field F.
-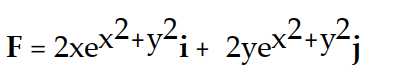
A)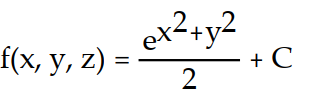
B)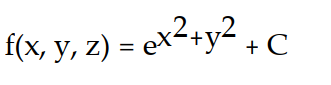
C)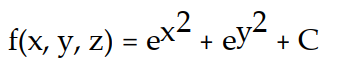
D)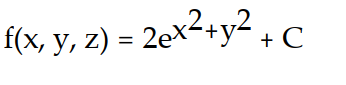
-
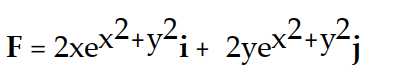
A)
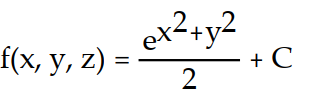
B)
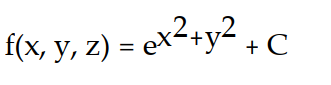
C)
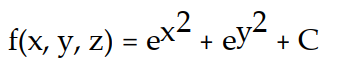
D)
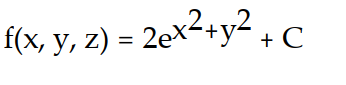

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
57
Find the potential function f for the field F.
-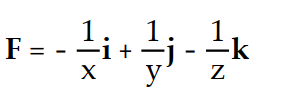
A)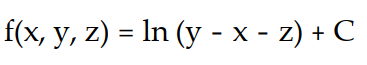
B)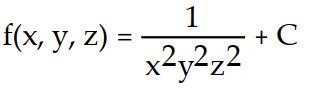
C)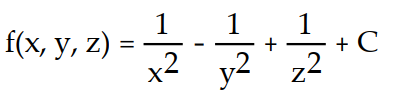
D)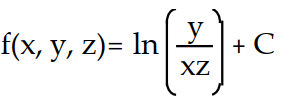
-
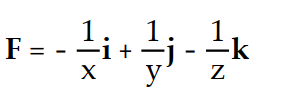
A)
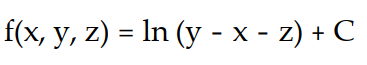
B)
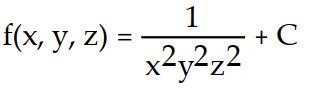
C)
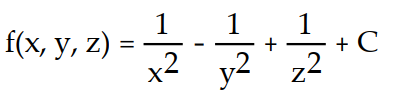
D)
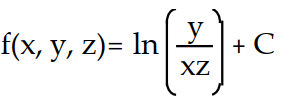

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
58
Find the potential function f for the field F.
-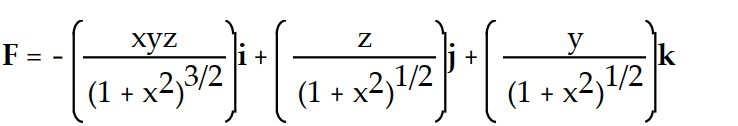
A)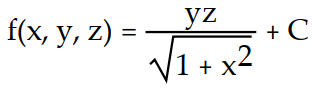
B)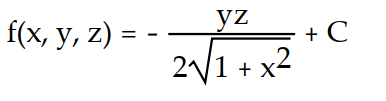
C)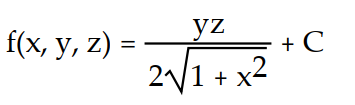
D)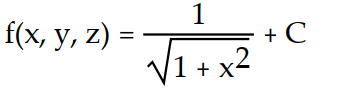
-
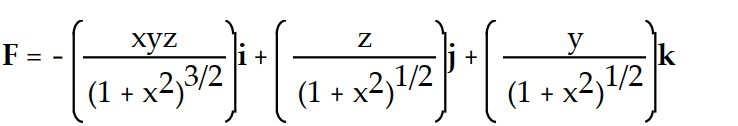
A)
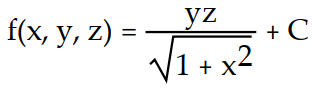
B)
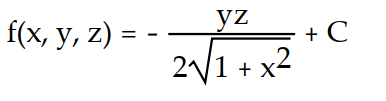
C)
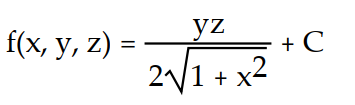
D)
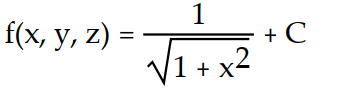

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
59
Find the potential function f for the field F.
-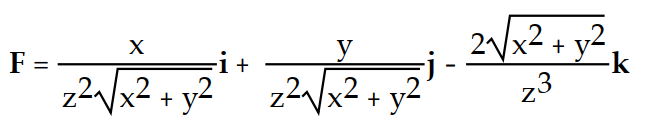
A)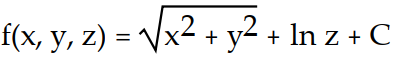
B)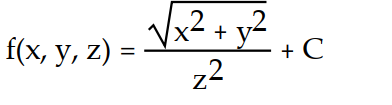
C)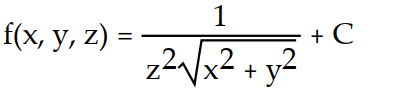
D)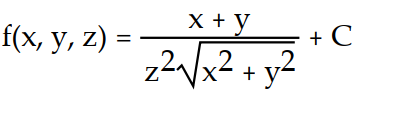
-
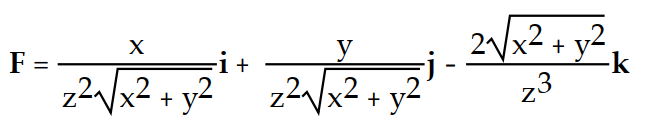
A)
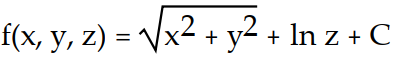
B)
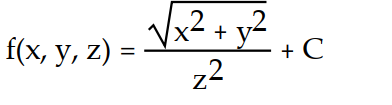
C)
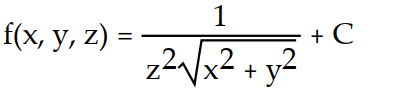
D)
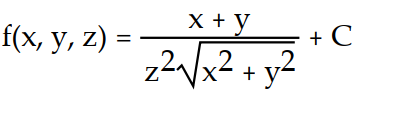

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
60
Find the potential function f for the field F.
-F = (y - z)i + (x + 2y - z)j - (x + y)k
A)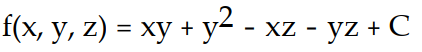
B)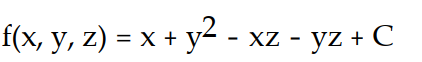
C)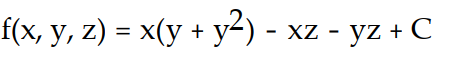
D)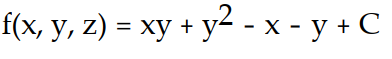
-F = (y - z)i + (x + 2y - z)j - (x + y)k
A)
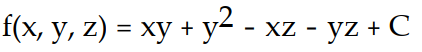
B)
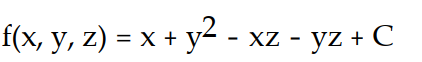
C)
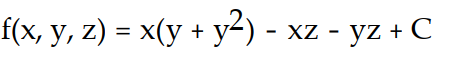
D)
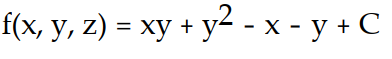

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
61
Evaluate the work done between point 1 and point 2 for the conservative field F.
-F = (y + z)i + xj + xk;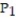 (0, 0, 0),
(0, 0, 0), 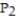 ( 3, 10, 7)
( 3, 10, 7)
A) W = 30
B) W = 51
C) W = 9
D) W = 0
-F = (y + z)i + xj + xk;
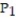 (0, 0, 0),
(0, 0, 0), 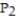 ( 3, 10, 7)
( 3, 10, 7)A) W = 30
B) W = 51
C) W = 9
D) W = 0

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
62
Evaluate the work done between point 1 and point 2 for the conservative field F.
-F = 6xi + 6yj + 6zk;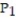 ( 4, 4, 5) ,
( 4, 4, 5) , 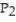 ( 6, 9, 6)
( 6, 9, 6)
A) W = 630
B) W = -288
C) W = 0
D) W = 288
-F = 6xi + 6yj + 6zk;
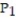 ( 4, 4, 5) ,
( 4, 4, 5) , 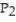 ( 6, 9, 6)
( 6, 9, 6)A) W = 630
B) W = -288
C) W = 0
D) W = 288

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
63
Evaluate the work done between point 1 and point 2 for the conservative field F.
-F = 4 sin 4x cos 7y cos 4zi + 7 cos 4x sin 7y cos 4zj + 4 cos 4x cos 7y sin 4zk ;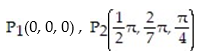
A) W = 1
B) W = -2
C) W = 0
D) W = 2
-F = 4 sin 4x cos 7y cos 4zi + 7 cos 4x sin 7y cos 4zj + 4 cos 4x cos 7y sin 4zk ;
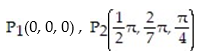
A) W = 1
B) W = -2
C) W = 0
D) W = 2

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
64
Evaluate the work done between point 1 and point 2 for the conservative field F.
-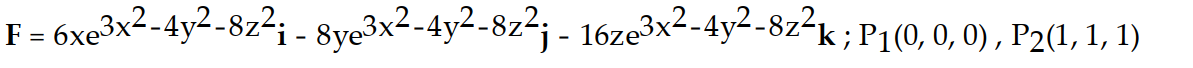
A) W =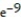 - 1
- 1
B) W =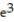 +
+ 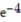 +
+ 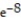 - 1
- 1
C) W =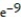
D) W = 0
-
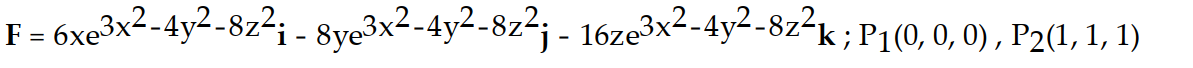
A) W =
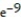 - 1
- 1B) W =
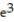 +
+ 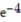 +
+ 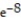 - 1
- 1C) W =
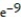
D) W = 0

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
65
Using Green's Theorem, compute the counterclockwise circulation of F around the closed curve C.
-F = (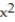 +
+ 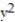 )i + (x - y)j; C is the rectangle with vertices at (0, 0), ( 3, 0), ( 3, 9), and (0, 9)
)i + (x - y)j; C is the rectangle with vertices at (0, 0), ( 3, 0), ( 3, 9), and (0, 9)
A) 0
B) 216
C) -216
D) 270
-F = (
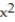 +
+ 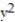 )i + (x - y)j; C is the rectangle with vertices at (0, 0), ( 3, 0), ( 3, 9), and (0, 9)
)i + (x - y)j; C is the rectangle with vertices at (0, 0), ( 3, 0), ( 3, 9), and (0, 9)A) 0
B) 216
C) -216
D) 270

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
66
Using Green's Theorem, compute the counterclockwise circulation of F around the closed curve C.
-F = sin 3yi + cos 9xj; C is the rectangle with vertices at (0, 0),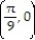 ,
, 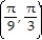 , and
, and 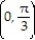
A) - 4/3
B) 0
C) - 2/3
D) 2/3
-F = sin 3yi + cos 9xj; C is the rectangle with vertices at (0, 0),
 ,
,  , and
, and 
A) - 4/3
B) 0
C) - 2/3
D) 2/3

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
67
Using Green's Theorem, compute the counterclockwise circulation of F around the closed curve C.
-F = (x - y)i + (x + y)j; C is the triangle with vertices at (0, 0), ( 3, 0), and (0, 10)
A) 30
B) 60
C) 300
D) 0
-F = (x - y)i + (x + y)j; C is the triangle with vertices at (0, 0), ( 3, 0), and (0, 10)
A) 30
B) 60
C) 300
D) 0

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
68
Using Green's Theorem, compute the counterclockwise circulation of F around the closed curve C.
-F = xyi + xj; C is the triangle with vertices at (0, 0), ( 7, 0), and (0, 7)
A) 0
B) 245/3
C) 343/6
D) - 98/3
-F = xyi + xj; C is the triangle with vertices at (0, 0), ( 7, 0), and (0, 7)
A) 0
B) 245/3
C) 343/6
D) - 98/3

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
69
Using Green's Theorem, compute the counterclockwise circulation of F around the closed curve C.
-F = ln (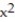 +
+ 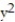 )i +
)i + 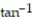
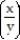 j; C is the region defined by the polar coordinate inequalities 1 r 7 and
j; C is the region defined by the polar coordinate inequalities 1 r 7 and 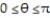
A) 96
B) -12
C) 50
D) 0
-F = ln (
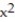 +
+ 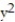 )i +
)i + 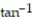
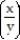 j; C is the region defined by the polar coordinate inequalities 1 r 7 and
j; C is the region defined by the polar coordinate inequalities 1 r 7 and 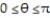
A) 96
B) -12
C) 50
D) 0

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
70
Using Green's Theorem, compute the counterclockwise circulation of F around the closed curve C.
-F = -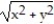 i +
i + 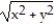 j; C is the region defined by the polar coordinate inequalities 8 r 9 and
j; C is the region defined by the polar coordinate inequalities 8 r 9 and 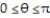
A) 0
B) 9
C) 34
D) 145
-F = -
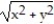 i +
i + 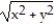 j; C is the region defined by the polar coordinate inequalities 8 r 9 and
j; C is the region defined by the polar coordinate inequalities 8 r 9 and 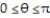
A) 0
B) 9
C) 34
D) 145

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
71
Using Green's Theorem, compute the counterclockwise circulation of F around the closed curve C.
-F = -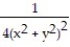 i; C is the region defined by the polar coordinate inequalities 1 r 4 and
i; C is the region defined by the polar coordinate inequalities 1 r 4 and 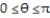
A) 65/96
B) 21/32
C) 0
D) - 21/32
-F = -
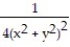 i; C is the region defined by the polar coordinate inequalities 1 r 4 and
i; C is the region defined by the polar coordinate inequalities 1 r 4 and 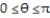
A) 65/96
B) 21/32
C) 0
D) - 21/32

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
72
Using Green's Theorem, compute the counterclockwise circulation of F around the closed curve C.
-F = ( 6x + 6y)i + ( 9x - 2y)j; C is the region bounded above by y = -5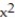 + 112 and below by
+ 112 and below by 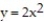 in the first quadrant
in the first quadrant
A) -1332
B) - 2180
C) 896
D) -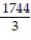
-F = ( 6x + 6y)i + ( 9x - 2y)j; C is the region bounded above by y = -5
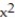 + 112 and below by
+ 112 and below by 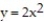 in the first quadrant
in the first quadrantA) -1332
B) - 2180
C) 896
D) -
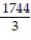

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
73
Using Green's Theorem, calculate the area of the indicated region.
-The area bounded above by y = 5x and below by y = 7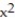
A) 125/147
B) 25/294
C) 625/588
D) 125/294
-The area bounded above by y = 5x and below by y = 7
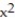
A) 125/147
B) 25/294
C) 625/588
D) 125/294

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
74
Using Green's Theorem, calculate the area of the indicated region.
-The area bounded above by y = 10 and below by y =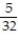
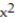
A) 160/3
B) 0
C) 640/3
D) 320/3
-The area bounded above by y = 10 and below by y =
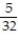
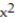
A) 160/3
B) 0
C) 640/3
D) 320/3

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
75
Using Green's Theorem, calculate the area of the indicated region.
-The area bounded above by y = 3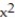 and below by y = 5
and below by y = 5 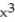
A) 27/250
B) 27/500
C) 27/1000
D) 27/125
-The area bounded above by y = 3
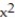 and below by y = 5
and below by y = 5 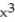
A) 27/250
B) 27/500
C) 27/1000
D) 27/125

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
76
Using Green's Theorem, calculate the area of the indicated region.
-The circle r(t) = ( 10 cos t)i + ( 10 sin t)j, 0 t 2
A) 10
B) 2
C) 20
D) 100
-The circle r(t) = ( 10 cos t)i + ( 10 sin t)j, 0 t 2
A) 10
B) 2
C) 20
D) 100

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
77
Using Green's Theorem, find the outward flux of F across the closed curve C.
-F =(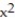 +
+ 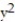 )i + (x - y)j ; C is the rectangle with vertices at (0, 0), ( 3, 0), ( 3, 10), and
)i + (x - y)j ; C is the rectangle with vertices at (0, 0), ( 3, 0), ( 3, 10), and 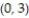
A) 120
B) 60
C) 330
D) -270
-F =(
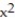 +
+ 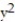 )i + (x - y)j ; C is the rectangle with vertices at (0, 0), ( 3, 0), ( 3, 10), and
)i + (x - y)j ; C is the rectangle with vertices at (0, 0), ( 3, 0), ( 3, 10), and 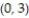
A) 120
B) 60
C) 330
D) -270

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
78
Using Green's Theorem, find the outward flux of F across the closed curve C.
-F = sin 6yi + cos 6xj ; C is the rectangle with vertices at (0, 0),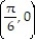 ,
, 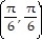 , and
, and 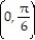
A) 0
B) - 1/3
C) 1/3
D) - 2/3
-F = sin 6yi + cos 6xj ; C is the rectangle with vertices at (0, 0),
 ,
, 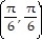 , and
, and 
A) 0
B) - 1/3
C) 1/3
D) - 2/3

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
79
Using Green's Theorem, find the outward flux of F across the closed curve C.
-F = ln (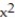 +
+ 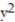 ) i +
) i + 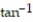
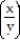 j; C is the region defined by the polar coordinate inequalities
j; C is the region defined by the polar coordinate inequalities 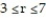 and
and 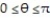
A) 0
B) 58
C) 80
D) 40
-F = ln (
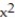 +
+ 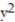 ) i +
) i + 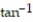
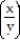 j; C is the region defined by the polar coordinate inequalities
j; C is the region defined by the polar coordinate inequalities 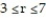 and
and 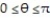
A) 0
B) 58
C) 80
D) 40

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck
80
Using Green's Theorem, find the outward flux of F across the closed curve C.
-F = -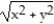 i +
i + 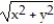 j ; C is the region defined by the polar coordinate inequalities
j ; C is the region defined by the polar coordinate inequalities 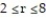 and
and 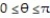
A) 0
B) 68
C) 60
D) 120
-F = -
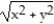 i +
i + 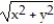 j ; C is the region defined by the polar coordinate inequalities
j ; C is the region defined by the polar coordinate inequalities 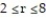 and
and 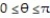
A) 0
B) 68
C) 60
D) 120

Unlock Deck
Unlock for access to all 173 flashcards in this deck.
Unlock Deck
k this deck


