Exam 17: Vector Calculus
Exam 1: Functions226 Questions
Exam 2: Limits224 Questions
Exam 3: Derivatives367 Questions
Exam 4: Applications of the Derivative228 Questions
Exam 5: Integration166 Questions
Exam 6: Applications of Integration211 Questions
Exam 7: Logarithmic, Exponential, and Hyperbolic Functions85 Questions
Exam 8: Integration Techniques287 Questions
Exam 9: Differential Equations76 Questions
Exam 10: Sequences and Infinite Series173 Questions
Exam 11: Power Series103 Questions
Exam 12: Parametric and Polar Curves169 Questions
Exam 13: Vectors and the Geometry of Space131 Questions
Exam 14: Vector-Valued Functions83 Questions
Exam 15: Functions of Several Variables229 Questions
Exam 16: Multiple Integration299 Questions
Exam 17: Vector Calculus173 Questions
Select questions type
Parametrize the surface S.
-S is the lower portion of the sphere 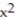 +
+ 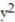 +
+ 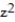 = 25 cut by the cone z =
= 25 cut by the cone z = 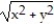 .
.
Free
(Essay)
4.9/5  (40)
(40)
Correct Answer:
Answers will vary. One possibility is r = 5 cos φ sin θi + 5 sin φ sin θj + 5 cos θk 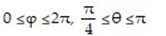
Parametrize the surface S.
-S is the portion of the cylinder 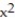 +
+ 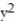 = 16 that lies between z = 2 and z = 7.
= 16 that lies between z = 2 and z = 7.
Free
(Essay)
4.8/5  (35)
(35)
Correct Answer:
Answers will vary. One possibility is r = 4 cos θi + 4 sin θj + zk , 2 ≤ z ≤ 7, 0 ≤ θ ≤ 2π
Use Stokes' Theorem to calculate the circulation of the field F around the curve C in the indicated direction.
-F = 2yi + 3xj + 6 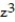 k ; C: the portion of the plane 3x + 3y + 5z = 6 in the first quadrant
k ; C: the portion of the plane 3x + 3y + 5z = 6 in the first quadrant
Free
(Multiple Choice)
5.0/5  (34)
(34)
Correct Answer:
D
Using Green's Theorem, compute the counterclockwise circulation of F around the closed curve C.
-F = xyi + xj; C is the triangle with vertices at (0, 0), ( 7, 0), and (0, 7)
(Multiple Choice)
4.8/5  (37)
(37)
Evaluate the work done between point 1 and point 2 for the conservative field F.
-F = (y + z)i + xj + xk; 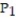 (0, 0, 0),
(0, 0, 0), 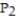 ( 3, 10, 7)
( 3, 10, 7)
(Multiple Choice)
4.8/5  (27)
(27)
Evaluate the work done between point 1 and point 2 for the conservative field F.
-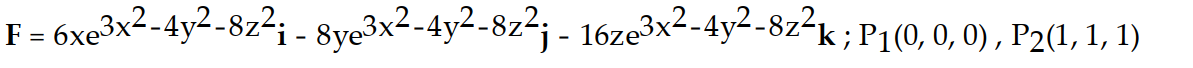
(Multiple Choice)
4.8/5  (42)
(42)
Find the mass of the wire that lies along the curve r and has density δ.
-r(t) = 7i + ( 9 - 4t)j + 3tk, 0 t 2 ; 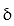 = 5(1 + sin 7t)
= 5(1 + sin 7t)
(Multiple Choice)
4.7/5  (31)
(31)
Find the flux of the vector field F across the surface S in the indicated direction.
-F(x, y, z) = 2xi + 2yj + 2k , S is the surface cut from the bottom of the paraboloid z = 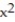 +
+ 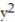 by the plane
by the plane 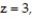 direction is outward
direction is outward
(Multiple Choice)
4.8/5  (29)
(29)
Find the surface area of the surface S.
-S is the intersection of the plane 3x + 4y + 12z = 7 and the cylinder with sides y = 4 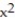 and y = 8 - 4
and y = 8 - 4 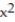 .
.
(Multiple Choice)
4.8/5  (36)
(36)
Sketch the vector field in the plane along with its horizontal and vertical components at a representative assortment of points on the circle x2 + y2 = 4.
-F = 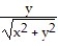 i +
i + 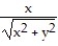 j
j
(Not Answered)
This question doesn't have any answer yet
Calculate the circulation of the field F around the closed curve C.
-F = xyi + 5j , curve C is r(t) = 3 cos ti + 3 sin tj, 0 t 2
(Multiple Choice)
4.8/5  (38)
(38)
Using the Divergence Theorem, find the outward flux of F across the boundary of the region D.
-F = 6 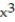 i + 6
i + 6 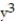 j + 6
j + 6 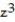 k ; D: the thick sphere 4
k ; D: the thick sphere 4 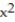 +
+ 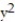 +
+ 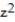 16
16
(Multiple Choice)
4.7/5  (35)
(35)
Using Green's Theorem, compute the counterclockwise circulation of F around the closed curve C.
-F = - 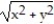 i +
i + 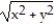 j; C is the region defined by the polar coordinate inequalities 8 r 9 and
j; C is the region defined by the polar coordinate inequalities 8 r 9 and 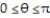
(Multiple Choice)
4.9/5  (34)
(34)
Parametrize the surface S.
-S is the portion of the cone 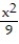 +
+ 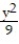 =
= 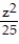 that lies between z = 1 and z = 9.
that lies between z = 1 and z = 9.
(Essay)
4.8/5  (29)
(29)
Find the gradient field F of the function f.
-f(x, y, z) = ln ( 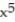 +
+ 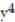 +
+ 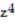 )
)
(Multiple Choice)
4.7/5  (39)
(39)
Calculate the flux of the field F across the closed plane curve C.
-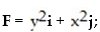 the curve C is the closed counterclockwise path formed from the semicircle
the curve C is the closed counterclockwise path formed from the semicircle  0 ≤ t ≤ π, and the straight line segment from (-4, 0) to ( 4, 0)
0 ≤ t ≤ π, and the straight line segment from (-4, 0) to ( 4, 0)
(Multiple Choice)
4.8/5  (34)
(34)
Evaluate the surface integral of the function g over the surface S.
-G(x, y, z) = x2 y2 z2 ; S is the surface of the rectangular prism formed from the planes x = ± 2, y = ± 2, and z = ± 1
(Multiple Choice)
4.9/5  (40)
(40)
Using the Divergence Theorem, find the outward flux of F across the boundary of the region D.
-F = x 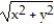 i + y
i + y 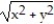 j + z
j + z 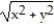 k ; D: the thick cylinder 1
k ; D: the thick cylinder 1 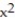 +
+ 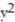 3 ,
3 , 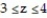
(Multiple Choice)
4.8/5  (41)
(41)
Showing 1 - 20 of 173
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)