Deck 15: Functions of Several Variables
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/229
Play
Full screen (f)
Deck 15: Functions of Several Variables
1
Find the domain and range and describe the level curves for the function f(x,y).
-f(x, y) = 4x + 3y
A) Domain: all points in the xy-plane; range: all real numbers; level curves: lines 4x + 3y = c, c > 0
B) Domain: all points in the xy-plane; range: all real numbers; level curves: lines 4x + 3y = c
C) Domain: all points in the xy-plane; range: real numbers z 0; level curves: lines 4x + 3y = c, c 0
D) Domain: all points in the xy-plane; range: real numbers z 0 ; level curves: lines 4x + 3y = c, c 0
-f(x, y) = 4x + 3y
A) Domain: all points in the xy-plane; range: all real numbers; level curves: lines 4x + 3y = c, c > 0
B) Domain: all points in the xy-plane; range: all real numbers; level curves: lines 4x + 3y = c
C) Domain: all points in the xy-plane; range: real numbers z 0; level curves: lines 4x + 3y = c, c 0
D) Domain: all points in the xy-plane; range: real numbers z 0 ; level curves: lines 4x + 3y = c, c 0
Domain: all points in the xy-plane; range: all real numbers; level curves: lines 4x + 3y = c, c > 0
2
Find the domain and range and describe the level curves for the function f(x,y).
-f(x, y) =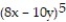
A) Domain: all points in the xy-plane; range: real numbers z ≤ 0; level curves: lines 8x - 10y = c, c ≤ 0
B) Domain: all points in the xy-plane; range: real numbers z ≥ 0; level curves: lines 8x - 10y = c
C) Domain: all points in the xy-plane; range: all real numbers; level curves: lines 8x - 10y = c, c ≥ 0
D) Domain: all points in the xy-plane; range: all real numbers; level curves: lines 8x - 10y = c
-f(x, y) =
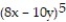
A) Domain: all points in the xy-plane; range: real numbers z ≤ 0; level curves: lines 8x - 10y = c, c ≤ 0
B) Domain: all points in the xy-plane; range: real numbers z ≥ 0; level curves: lines 8x - 10y = c
C) Domain: all points in the xy-plane; range: all real numbers; level curves: lines 8x - 10y = c, c ≥ 0
D) Domain: all points in the xy-plane; range: all real numbers; level curves: lines 8x - 10y = c
Domain: all points in the xy-plane; range: all real numbers; level curves: lines 8x - 10y = c
3
Find the domain and range and describe the level curves for the function f(x,y).
-f(x, y) =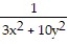
A) Domain: all points in the xy-plane; range: real numbers > 0; level curves: ellipses 3x2 + 10y2 = c
B) Domain: all points in the xy-plane except (0, 0); range: real numbers > 0; level curves: ellipses 3x2 + 10y2 = c
C) Domain: all points in the xy-plane; range: all real numbers; level curves: ellipses 3x2 + 10y2 = c
D) Domain: all points in the xy-plane except (0, 0); range: all real numbers; level curves: ellipses 3x2 + 10y2 = c
-f(x, y) =
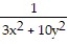
A) Domain: all points in the xy-plane; range: real numbers > 0; level curves: ellipses 3x2 + 10y2 = c
B) Domain: all points in the xy-plane except (0, 0); range: real numbers > 0; level curves: ellipses 3x2 + 10y2 = c
C) Domain: all points in the xy-plane; range: all real numbers; level curves: ellipses 3x2 + 10y2 = c
D) Domain: all points in the xy-plane except (0, 0); range: all real numbers; level curves: ellipses 3x2 + 10y2 = c
Domain: all points in the xy-plane except (0, 0); range: real numbers > 0; level curves: ellipses 3x2 + 10y2 = c
4
Find the domain and range and describe the level curves for the function f(x,y).
-f(x, y) =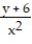
A) Domain: all points in the xy-plane; range: all real numbers; level curves: parabolas y= cx2 - 6
B) Domain: all points in the xy-plane; range: real numbers z ≥ 0; level curves: parabolas y= cx2 - 6
C) Domain: all points in the xy-plane excluding x = 0; range: all real numbers; level curves: parabolas y= cx2 - 6
D) Domain: all points in the xy-plane excluding x = 0; range: real numbers z ≥ 0; level curves: parabolas y= cx2 - 6
-f(x, y) =
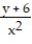
A) Domain: all points in the xy-plane; range: all real numbers; level curves: parabolas y= cx2 - 6
B) Domain: all points in the xy-plane; range: real numbers z ≥ 0; level curves: parabolas y= cx2 - 6
C) Domain: all points in the xy-plane excluding x = 0; range: all real numbers; level curves: parabolas y= cx2 - 6
D) Domain: all points in the xy-plane excluding x = 0; range: real numbers z ≥ 0; level curves: parabolas y= cx2 - 6

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
5
Find the domain and range and describe the level curves for the function f(x,y).
-f(x, y) = ln ( 7x + 10y)
A) Domain: all points in the xy-plane; range: all real numbers; level curves: lines 7x + 10y = c
B) Domain: all points in the xy-plane satisfying 7x + 10y > 0; range: all real numbers; level curves: lines 7x + 10y = c
C) Domain: all points in the xy-plane satisfying 7x + 10y ≥ 0; range: all real numbers; level curves: lines 7x + 10y = c
D) Domain: all points in the xy-plane satisfying 7x + 10y > 0; range: real numbers z ≥ 0; level curves: 7x + 10y = c lines
-f(x, y) = ln ( 7x + 10y)
A) Domain: all points in the xy-plane; range: all real numbers; level curves: lines 7x + 10y = c
B) Domain: all points in the xy-plane satisfying 7x + 10y > 0; range: all real numbers; level curves: lines 7x + 10y = c
C) Domain: all points in the xy-plane satisfying 7x + 10y ≥ 0; range: all real numbers; level curves: lines 7x + 10y = c
D) Domain: all points in the xy-plane satisfying 7x + 10y > 0; range: real numbers z ≥ 0; level curves: 7x + 10y = c lines

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
6
Find the domain and range and describe the level curves for the function f(x,y).
-f(x, y) =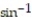 (
( 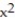 +
+ 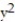 )
)
A) Domain: all points in the xy-plane; range: all real numbers; level curves: circles with centers at (0, 0)
B) Domain: all points in the xy-plane satisfying x2 + y2 ≤ 1; range: real numbers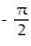 ≤ z ≤
≤ z ≤ 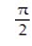 ; level curves: circles with centers at (0, 0)
; level curves: circles with centers at (0, 0)
C) Domain: all points in the xy-plane satisfying x2 + y2 ≤ 1; range: real numbers - 11efabfd_aa12_34a1_af07_d19efc43c81a_TB9662_00 ≤ z ≤11efabfd_aa12_34a1_af07_d19efc43c81a_TB9662_00 ; level curves: circles with centers at (0,0) and radii r, 0 < r ≤ 1
D) Domain: all points in the xy-plane; range: real numbers - 11efabfd_aa12_34a1_af07_d19efc43c81a_TB9662_00 ≤ z ≤ 11efabfd_aa12_34a1_af07_d19efc43c81a_TB9662_00 ; level curves: circles with centers at (0, 0)
-f(x, y) =
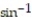 (
( 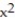 +
+ 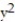 )
)A) Domain: all points in the xy-plane; range: all real numbers; level curves: circles with centers at (0, 0)
B) Domain: all points in the xy-plane satisfying x2 + y2 ≤ 1; range: real numbers
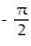 ≤ z ≤
≤ z ≤ 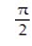 ; level curves: circles with centers at (0, 0)
; level curves: circles with centers at (0, 0) C) Domain: all points in the xy-plane satisfying x2 + y2 ≤ 1; range: real numbers - 11efabfd_aa12_34a1_af07_d19efc43c81a_TB9662_00 ≤ z ≤11efabfd_aa12_34a1_af07_d19efc43c81a_TB9662_00 ; level curves: circles with centers at (0,0) and radii r, 0 < r ≤ 1
D) Domain: all points in the xy-plane; range: real numbers - 11efabfd_aa12_34a1_af07_d19efc43c81a_TB9662_00 ≤ z ≤ 11efabfd_aa12_34a1_af07_d19efc43c81a_TB9662_00 ; level curves: circles with centers at (0, 0)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
7
Find the domain and range and describe the level curves for the function f(x,y).
-f(x, y) =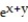
A) Domain: all points in the first quadrant of the xy-plane; range: all real numbers; level curves: lines x + y = c
B) Domain: all points in the first quadrant of the xy-plane; range: real numbers z > 0; level curves: lines x + y = c
C) Domain: all points in the xy-plane; range: real numbers z > 0; level curves: lines x + y = c
D) Domain: all points in the xy-plane; range: all real numbers; level curves: lines x + y = c
-f(x, y) =
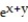
A) Domain: all points in the first quadrant of the xy-plane; range: all real numbers; level curves: lines x + y = c
B) Domain: all points in the first quadrant of the xy-plane; range: real numbers z > 0; level curves: lines x + y = c
C) Domain: all points in the xy-plane; range: real numbers z > 0; level curves: lines x + y = c
D) Domain: all points in the xy-plane; range: all real numbers; level curves: lines x + y = c

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
8
Find the domain and range and describe the level curves for the function f(x,y).
-f(x, y) =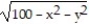
A) Domain: all points in the xy-plane satisfying x2 + y2 = 100; range: real numbers 0 ≤ z ≤ 10; level curves: circles with centers at (0, 0) and radii r, 0 < r ≤ 10
B) Domain: all points in the xy-plane satisfying x2 + y2 ≤ 100; range: real numbers 0 ≤ z ≤ 10; level curves: circles with centers at (0, 0) and radii r, 0 < r ≤ 10
C) Domain: all points in the xy-plane; range: real numbers 0 ≤ z ≤ 10; level curves: circles with centers at (0, 0) and radii r, 0 < r ≤ 10
D) Domain: all points in the xy-plane; range: all real numbers; level curves: circles with centers at (0,0)
-f(x, y) =
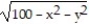
A) Domain: all points in the xy-plane satisfying x2 + y2 = 100; range: real numbers 0 ≤ z ≤ 10; level curves: circles with centers at (0, 0) and radii r, 0 < r ≤ 10
B) Domain: all points in the xy-plane satisfying x2 + y2 ≤ 100; range: real numbers 0 ≤ z ≤ 10; level curves: circles with centers at (0, 0) and radii r, 0 < r ≤ 10
C) Domain: all points in the xy-plane; range: real numbers 0 ≤ z ≤ 10; level curves: circles with centers at (0, 0) and radii r, 0 < r ≤ 10
D) Domain: all points in the xy-plane; range: all real numbers; level curves: circles with centers at (0,0)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
9
Find the domain and range and describe the level curves for the function f(x,y).
-f(x, y) =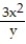
A) Domain: all points in the xy-plane except y = 0; range: all real numbers; level curves: parabolas y = cx2
B) Domain: all points in the xy-plane; range: real numbers z ≥ 0; level curves: parabolas y = cx2
C) Domain: all points in the xy-plane except y = 0; range: real numbers z ≥ 0 ; level curves: parabolas y = cx2
D) Domain: all points in the xy-plane; range: all real numbers; level curves: parabolas y = cx2
-f(x, y) =
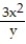
A) Domain: all points in the xy-plane except y = 0; range: all real numbers; level curves: parabolas y = cx2
B) Domain: all points in the xy-plane; range: real numbers z ≥ 0; level curves: parabolas y = cx2
C) Domain: all points in the xy-plane except y = 0; range: real numbers z ≥ 0 ; level curves: parabolas y = cx2
D) Domain: all points in the xy-plane; range: all real numbers; level curves: parabolas y = cx2

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
10
Find the domain and range and describe the level curves for the function f(x,y).
-f(x, y) = 3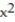 - 5
- 5 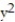
A) Domain: all points in the xy-plane; range: all real numbers; level curves: hyperbolas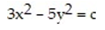
B) Domain: all points in the xy-plane; range: real numbers z ≥ 0; level curves: ellipses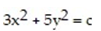
C) Domain: all points in the xy-plane; range: all real numbers; level curves: ellipses 11efabfe_b7a2_fea3_af07_277d2671e3df_TB9662_00
D) Domain: all points in the first quadrant of the xy-plane; range: all real numbers; level curves: hyperbolas 11efabfe_a41f_4462_af07_c3f2d3c3a269_TB9662_00
-f(x, y) = 3
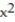 - 5
- 5 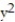
A) Domain: all points in the xy-plane; range: all real numbers; level curves: hyperbolas
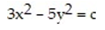
B) Domain: all points in the xy-plane; range: real numbers z ≥ 0; level curves: ellipses
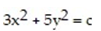
C) Domain: all points in the xy-plane; range: all real numbers; level curves: ellipses 11efabfe_b7a2_fea3_af07_277d2671e3df_TB9662_00
D) Domain: all points in the first quadrant of the xy-plane; range: all real numbers; level curves: hyperbolas 11efabfe_a41f_4462_af07_c3f2d3c3a269_TB9662_00

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
11
Sketch the surface z = f(x,y).
-f(x, y) =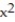
A)
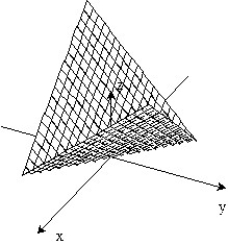
B)
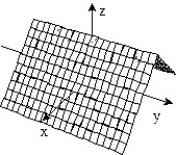
C)
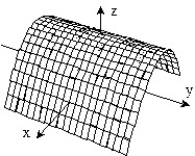
D)
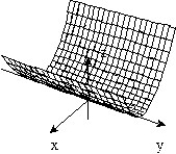
-f(x, y) =
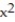
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
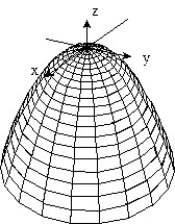
12
Sketch the surface z = f(x,y).
-f(x, y) = -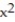 -
- 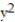
A)
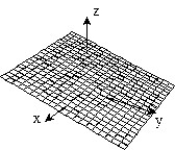
B)
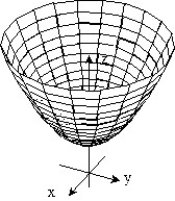
C)
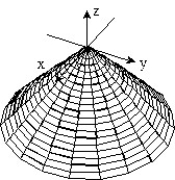
D)
-f(x, y) = -
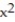 -
- 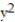
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
13
Sketch the surface z = f(x,y).
-f(x, y) = 3 -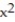
A)
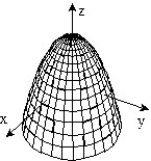
B)
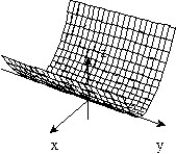
C)
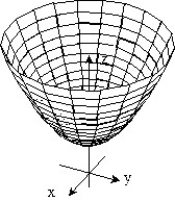
D)
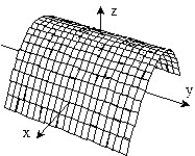
-f(x, y) = 3 -
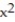
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
14
Sketch the surface z = f(x,y).
-f(x, y) = -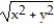
A)
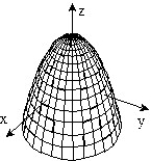
B)
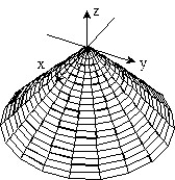
C)
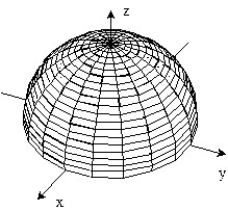
D)
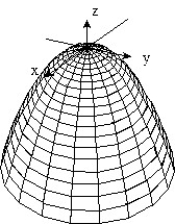
-f(x, y) = -
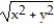
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
15
Sketch the surface z = f(x,y).
-f(x, y) =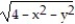
A)
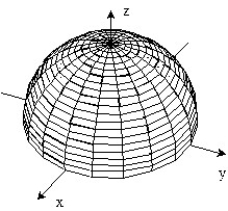
B)
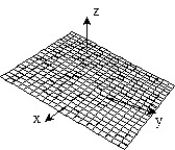
C)
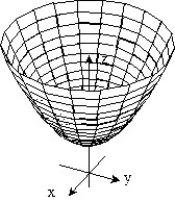
D)
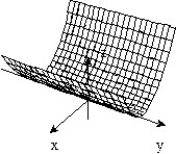
-f(x, y) =
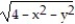
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
16
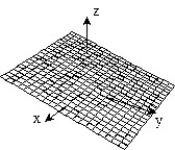
Sketch the surface z = f(x,y).
-f(x, y) =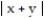
A)
B)
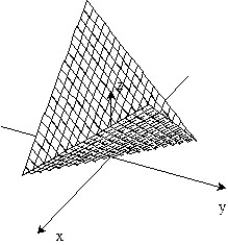
C)
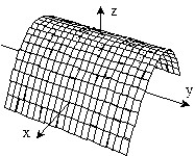
D)
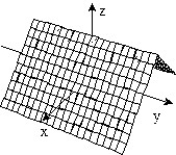
-f(x, y) =
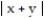
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
17
Sketch the surface z = f(x,y).
-f(x, y) = 4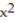 + 4
+ 4 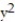 + 2
+ 2
A)
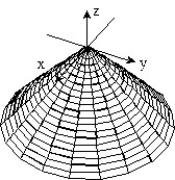
B)
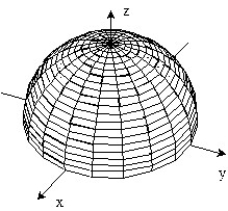
C)
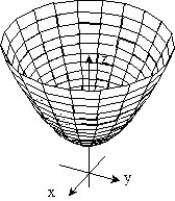
D)
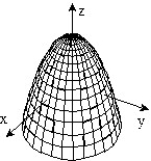
-f(x, y) = 4
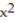 + 4
+ 4 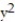 + 2
+ 2A)

B)

C)

D)


Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
18
Sketch the surface z = f(x,y).
-f(x, y) = 1 -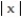
A)
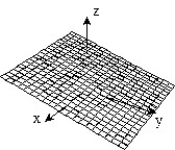
B)
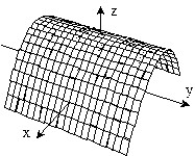
C)
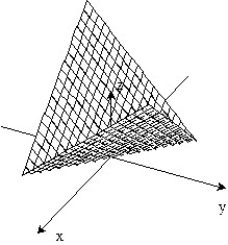
D)
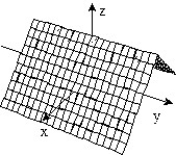
-f(x, y) = 1 -
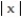
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
19
Sketch the surface z = f(x,y).
-f(x, y) = 2 -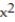 -
- 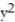
A)
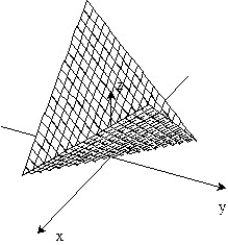
B)
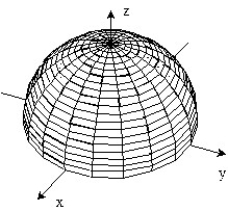
C)
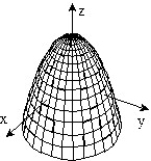
D)
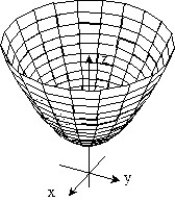
-f(x, y) = 2 -
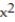 -
- 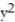
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
20
Sketch the surface z = f(x,y).
-f(x, y) = 1 - x - 2y
A)
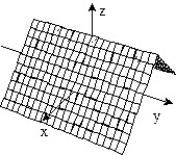
B)
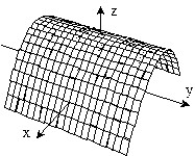
C)
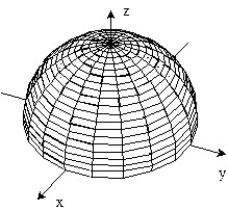
D)
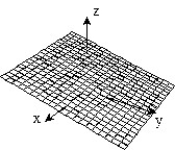
-f(x, y) = 1 - x - 2y
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
21
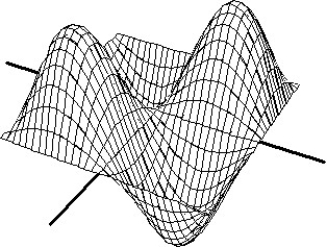
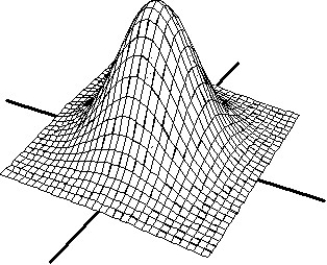
Match the surface show below to the graph of its level curves.
-
A)
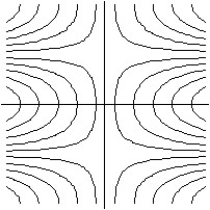
B)
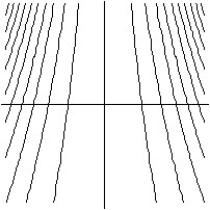
C)
D)
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
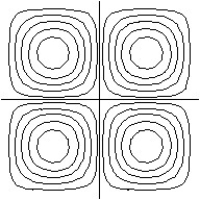
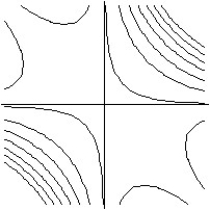
22
Match the surface show below to the graph of its level curves.
-
A)
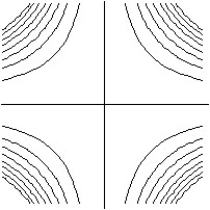
B)
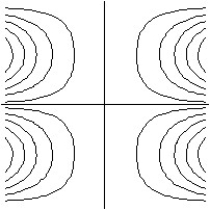
C)
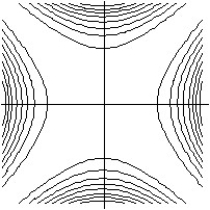
D)
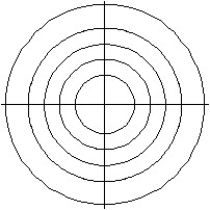
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
23
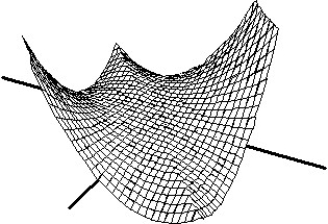
Match the surface show below to the graph of its level curves.
-
A)
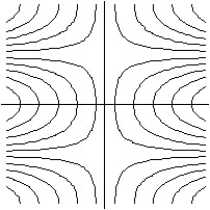
B)
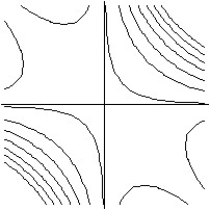
C)
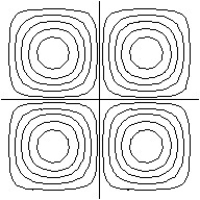
D)
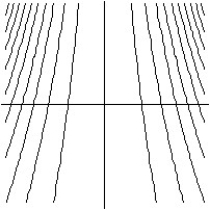
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
24
Match the surface show below to the graph of its level curves.
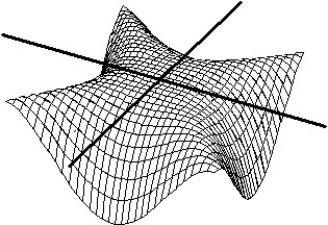
-
A)
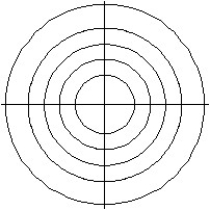
B)
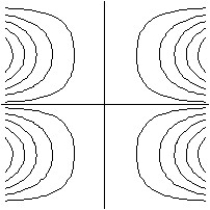
C)
D)
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
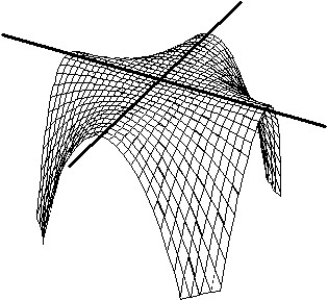
25
Match the surface show below to the graph of its level curves.
-
A)
B)
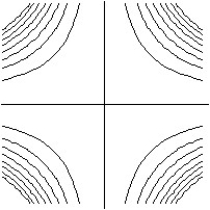
C)
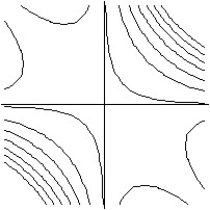
D)
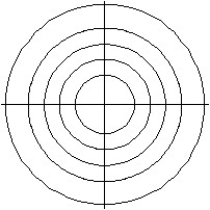
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
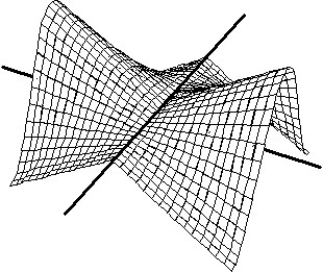
26
Match the surface show below to the graph of its level curves.
-
A)
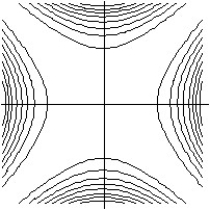
B)
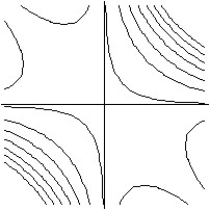
C)
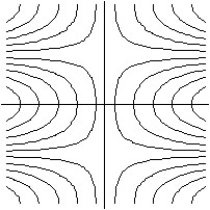
D)
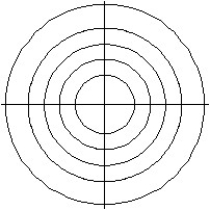
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
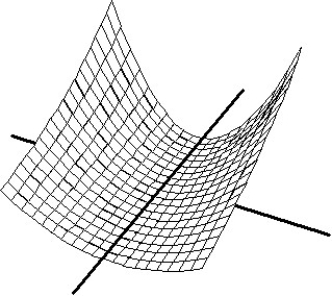
27
Match the surface show below to the graph of its level curves.
-
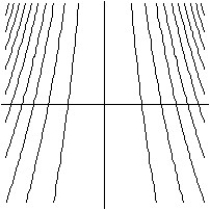
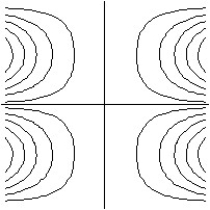
A)
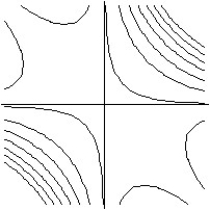
B)
C)
D)
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
28
Match the surface show below to the graph of its level curves.
-
A)
B)
C)
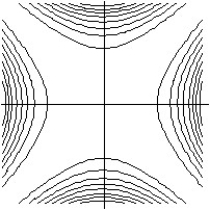
D)
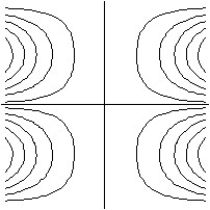
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
29
Solve the problem.
-According to the Gas Kinetic Theory, the average speed of a gas particle is given by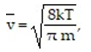 where
where
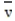 is the speed in m/s, k is the constant 1.38 × 10-23 , T is the temperature of the gas in Kelvin, and m is the mass of the gas particle in kg. What is the average speed of an oxygen molecule with a mass of
is the speed in m/s, k is the constant 1.38 × 10-23 , T is the temperature of the gas in Kelvin, and m is the mass of the gas particle in kg. What is the average speed of an oxygen molecule with a mass of
5.314 X 10-26 KG at a temperature of 500 K?
A) 1020 m/s
B) 575 m/s
C) 330,700 m/s
D) 174 m/s
-According to the Gas Kinetic Theory, the average speed of a gas particle is given by
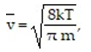 where
where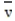 is the speed in m/s, k is the constant 1.38 × 10-23 , T is the temperature of the gas in Kelvin, and m is the mass of the gas particle in kg. What is the average speed of an oxygen molecule with a mass of
is the speed in m/s, k is the constant 1.38 × 10-23 , T is the temperature of the gas in Kelvin, and m is the mass of the gas particle in kg. What is the average speed of an oxygen molecule with a mass of5.314 X 10-26 KG at a temperature of 500 K?
A) 1020 m/s
B) 575 m/s
C) 330,700 m/s
D) 174 m/s

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
30
Write the word or phrase that best completes each statement or answers the question.
-The Ideal Gas Law states that the pressure P of a gas obeys the function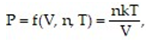 where n is the number of particles in the sample, T is the Kelvin temperature of the gas, V is the volume of the gas in liters, and k is the constant 1.38 × 10-23 . Does the pressure have a local minimum along the line
where n is the number of particles in the sample, T is the Kelvin temperature of the gas, V is the volume of the gas in liters, and k is the constant 1.38 × 10-23 . Does the pressure have a local minimum along the line 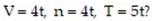 If so, what is the value of the minimum pressure? Give reasons for your answer.
If so, what is the value of the minimum pressure? Give reasons for your answer.
-The Ideal Gas Law states that the pressure P of a gas obeys the function
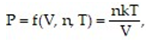 where n is the number of particles in the sample, T is the Kelvin temperature of the gas, V is the volume of the gas in liters, and k is the constant 1.38 × 10-23 . Does the pressure have a local minimum along the line
where n is the number of particles in the sample, T is the Kelvin temperature of the gas, V is the volume of the gas in liters, and k is the constant 1.38 × 10-23 . Does the pressure have a local minimum along the line 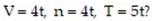 If so, what is the value of the minimum pressure? Give reasons for your answer.
If so, what is the value of the minimum pressure? Give reasons for your answer. 
Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
31
Write the word or phrase that best completes each statement or answers the question.
-A sample of matter has a temperature distribution given by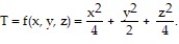 Describe the level surfaces and write an equation for the surface T = 300.
Describe the level surfaces and write an equation for the surface T = 300.
-A sample of matter has a temperature distribution given by
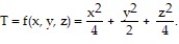 Describe the level surfaces and write an equation for the surface T = 300.
Describe the level surfaces and write an equation for the surface T = 300.
Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
32
Find the limit.
-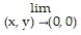
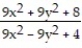
A) 2
B) 1
C) -1
D) No limit
-
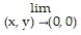
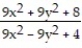
A) 2
B) 1
C) -1
D) No limit

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
33
Find the limit.
-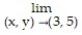
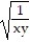
A)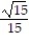
B)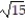
C) 15
D) No limit
-
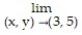
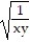
A)
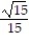
B)
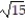
C) 15
D) No limit

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
34
Find the limit.
-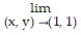 ln
ln 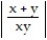
A) 0
B) ln 2
C) -ln 2
D) No limit
-
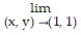 ln
ln 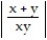
A) 0
B) ln 2
C) -ln 2
D) No limit

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
35
Find the limit.
-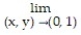
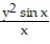
A) 1
B)
C) 0
D) No limit
-
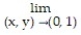
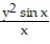
A) 1
B)
C) 0
D) No limit

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
36
Find the limit.
-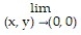 sin
sin 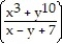
A) 1
B) 1/7
C) 0
D) No limit
-
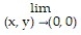 sin
sin 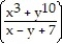
A) 1
B) 1/7
C) 0
D) No limit

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
37
Find the limit.
-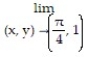
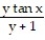
A) 1/2
B) 2
C) 0
D)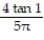
-
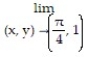
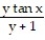
A) 1/2
B) 2
C) 0
D)
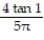

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
38
Find the limit.
-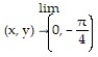
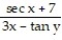
A) -8
B)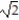 + 7
+ 7
C) -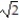 - 7
- 7
D) 8
-
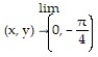
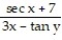
A) -8
B)
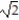 + 7
+ 7C) -
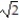 - 7
- 7D) 8

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
39
Find the limit.
-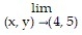
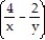
A) - 3/5
B) 12
C) 3/5
D) No limit
-
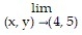
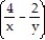
A) - 3/5
B) 12
C) 3/5
D) No limit

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
40
Find the limit.
-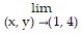 x ln y
x ln y
A) 4
B) ln 4
C) ln ( 4) - 1
D) No limit
-
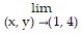 x ln y
x ln yA) 4
B) ln 4
C) ln ( 4) - 1
D) No limit

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
41
Find the limit.
-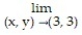
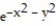
A) 1
B)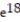
C) 0
D)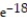
-
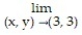
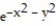
A) 1
B)
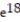
C) 0
D)
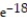

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
42
Find the limit.
-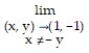
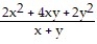
A) 1
B) 0
C) 1/2
D) No limit
-
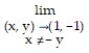
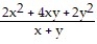
A) 1
B) 0
C) 1/2
D) No limit

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
43
Find the limit.
-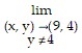
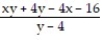
A) 13
B) 1
C) 5
D) 0
-
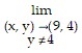
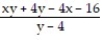
A) 13
B) 1
C) 5
D) 0

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
44
Find the limit.
-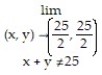
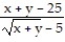
A) 0
B) 10
C) 5
D) No limit
-
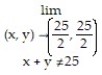
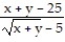
A) 0
B) 10
C) 5
D) No limit

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
45
Find the limit.
-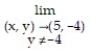
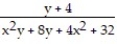
A) 1/33
B) 17
C) 0
D) 33
-
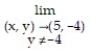
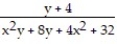
A) 1/33
B) 17
C) 0
D) 33

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
46
Find the limit.
-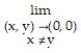
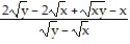
A) 0
B) 2
C) 4
D) No limit
-
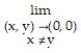
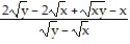
A) 0
B) 2
C) 4
D) No limit

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
47
Find the limit.
-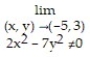
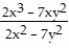
A) 3
B) -5
C)
D) 0
-
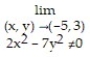
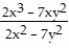
A) 3
B) -5
C)
D) 0

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
48
Find two paths of approach from which one can conclude that the function has no limit as (x, y) approaches (0, 0).
-f(x, y) =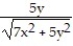
-f(x, y) =
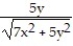

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
49
Find two paths of approach from which one can conclude that the function has no limit as (x, y) approaches (0, 0).
-f(x, y) =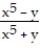
-f(x, y) =
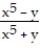

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
50
Find two paths of approach from which one can conclude that the function has no limit as (x, y) approaches (0, 0).
-f(x, y) =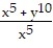
-f(x, y) =
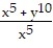

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
51
Find two paths of approach from which one can conclude that the function has no limit as (x, y) approaches (0, 0).
-f(x, y) =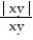
-f(x, y) =
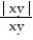

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
52
Find two paths of approach from which one can conclude that the function has no limit as (x, y) approaches (0, 0).
-f(x, y) =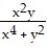
-f(x, y) =
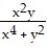

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
53
Find two paths of approach from which one can conclude that the function has no limit as (x, y) approaches (0, 0).
-f(x, y) =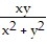
-f(x, y) =
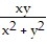

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
54
Find two paths of approach from which one can conclude that the function has no limit as (x, y) approaches (0, 0).
-f(x, y) =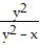
-f(x, y) =
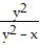

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
55
Find two paths of approach from which one can conclude that the function has no limit as (x, y) approaches (0, 0).
-f(x, y) =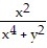
-f(x, y) =
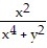

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
56
At what points is the given function continuous?
-f(x, y) =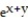
A) All (x, y) (0, 0)
B) All (x, y) satisfying x + y 0
C) All (x, y)
D) All (x, y) in the first quadrant
-f(x, y) =
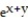
A) All (x, y) (0, 0)
B) All (x, y) satisfying x + y 0
C) All (x, y)
D) All (x, y) in the first quadrant

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
57
At what points is the given function continuous?
-f(x, y) =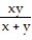
A) All (x, y) such that x y
B) All (x, y) (0, 0)
C) All (x, y) such that x - y
D) All (x, y)
-f(x, y) =
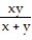
A) All (x, y) such that x y
B) All (x, y) (0, 0)
C) All (x, y) such that x - y
D) All (x, y)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
58
At what points is the given function continuous?
-f(x, y) = tan (x + y)
A) All (x, y) (0, 0)
B) All (x, y)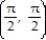
C) All (x, y) such that x + y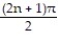 , where n is an integer
, where n is an integer
D) All (x, y)
-f(x, y) = tan (x + y)
A) All (x, y) (0, 0)
B) All (x, y)
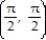
C) All (x, y) such that x + y
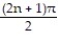 , where n is an integer
, where n is an integerD) All (x, y)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
59
At what points is the given function continuous?
-f(x, y) =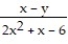
A)All (x, y) such that x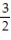 and x -2
and x -2
B) All (x, y)
C) All (x, y) such that x 0
D) All (x, y) satisfying x - y 0
-f(x, y) =
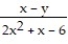
A)All (x, y) such that x
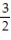 and x -2
and x -2B) All (x, y)
C) All (x, y) such that x 0
D) All (x, y) satisfying x - y 0

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
60
At what points is the given function continuous?
-f(x, y) =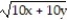
A) All (x, y) such that 10x + 10y 0
B) All (x, y) such that x + y 0
C) All (x, y) such that 10x + 10y 0.
D) All (x, y)
-f(x, y) =
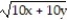
A) All (x, y) such that 10x + 10y 0
B) All (x, y) such that x + y 0
C) All (x, y) such that 10x + 10y 0.
D) All (x, y)

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
61
Find the limit.
-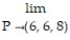
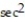 x -
x - 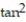 y + z
y + z
A) 8
B) 9
C) 6
D) 7
-
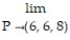
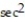 x -
x - 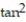 y + z
y + zA) 8
B) 9
C) 6
D) 7

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
62
Find the limit.
-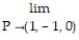
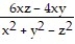
A) 2
B) 6
C) -6
D) -4
-
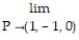
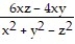
A) 2
B) 6
C) -6
D) -4

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
63
Find the limit.
-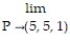 ln (z
ln (z 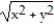 )
)
A) ln 5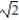
B) 0
C) ln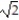
D) ln 25
-
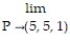 ln (z
ln (z 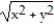 )
)A) ln 5
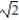
B) 0
C) ln
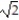
D) ln 25

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
64
Find the limit.
-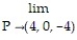
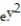
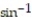
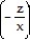
A) 1
B)
C) 0
D) /2
-
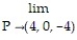
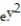
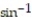
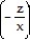
A) 1
B)
C) 0
D) /2

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
65
Use polar coordinates to find the limit of the function as (x, y) approaches (0, 0).
-f(x, y) =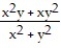
A) 1
B) 2
C) 0
D) No limit
-f(x, y) =
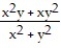
A) 1
B) 2
C) 0
D) No limit

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
66
Use polar coordinates to find the limit of the function as (x, y) approaches (0, 0).
-f(x, y) =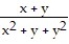
A) 0
B) 2
C) 1
D) No limit
-f(x, y) =
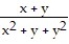
A) 0
B) 2
C) 1
D) No limit

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
67
Use polar coordinates to find the limit of the function as (x, y) approaches (0, 0).
-f(x, y) = cos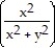
A) /2
B) 0
C) 1
D) No limit
-f(x, y) = cos
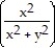
A) /2
B) 0
C) 1
D) No limit

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
68
Use polar coordinates to find the limit of the function as (x, y) approaches (0, 0).
-f(x, y) =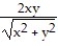
A)
B) 1
C) 0
D) -1
-f(x, y) =
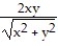
A)
B) 1
C) 0
D) -1

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
69
Use polar coordinates to find the limit of the function as (x, y) approaches (0, 0).
-f(x, y) =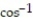
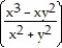
A) /2
B)
C) 1
D) No limit
-f(x, y) =
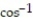
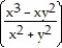
A) /2
B)
C) 1
D) No limit

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
70
Use polar coordinates to find the limit of the function as (x, y) approaches (0, 0).
-f(x, y) =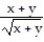
A) 0
B)
C) 1
D) No limit
-f(x, y) =
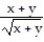
A) 0
B)
C) 1
D) No limit

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
71
Find all the first order partial derivatives for the following function.
-f(x, y) = 10x - 3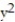 - 6
- 6
A)
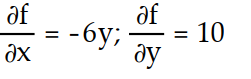
B)
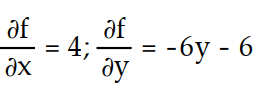
C)
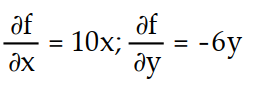
D)
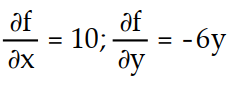
-f(x, y) = 10x - 3
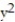 - 6
- 6A)
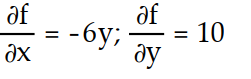
B)
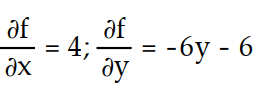
C)
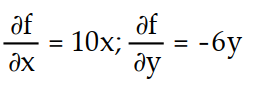
D)
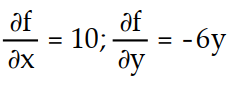

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
72
Find all the first order partial derivatives for the following function.
-f(x, y) =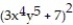
A)
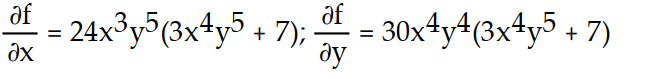
B)
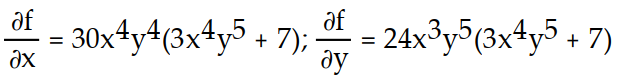
C)
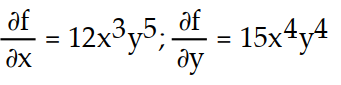
D)
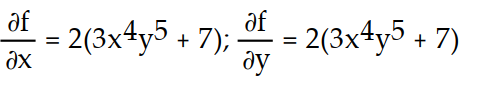
-f(x, y) =
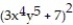
A)
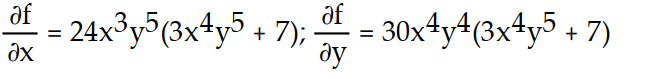
B)
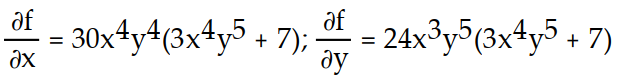
C)
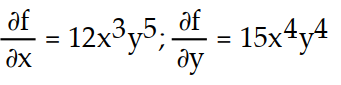
D)
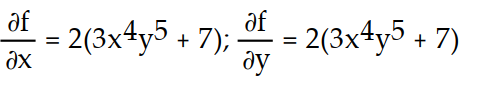

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
73
Find all the first order partial derivatives for the following function.
-f(x, y) =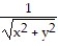
A)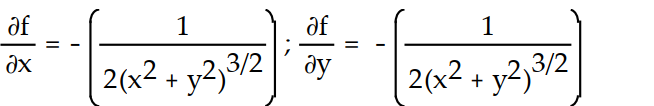
B)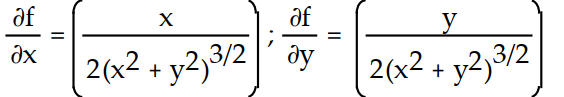
C)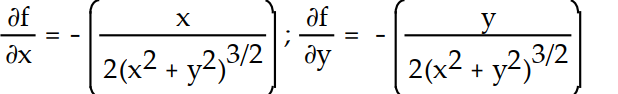
D)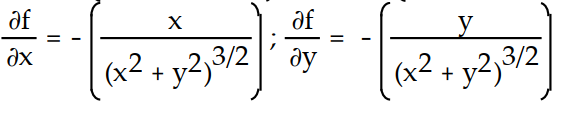
-f(x, y) =
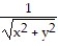
A)
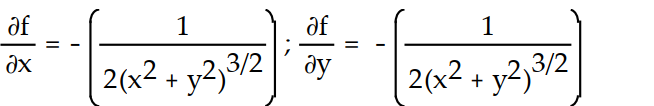
B)
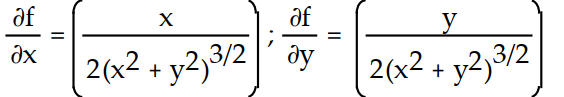
C)
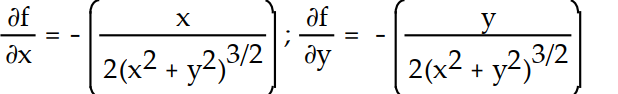
D)
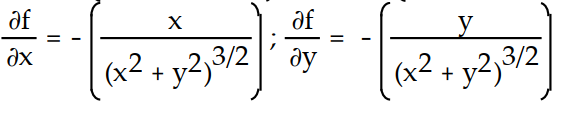

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
74
Find all the first order partial derivatives for the following function.
-f(x, y) = ln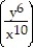
A)
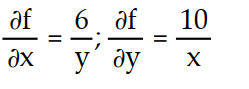
B)
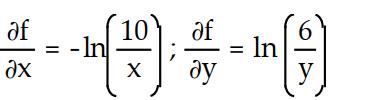
C)
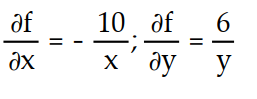
D)
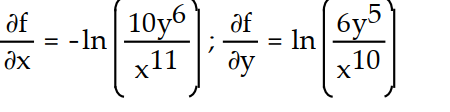
-f(x, y) = ln
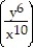
A)
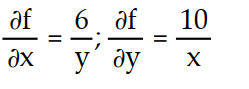
B)
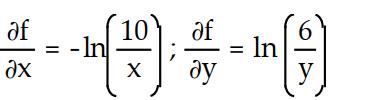
C)
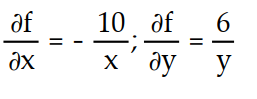
D)
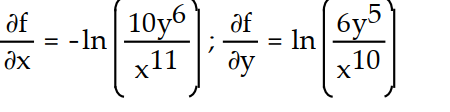

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
75
Find all the first order partial derivatives for the following function.
-f(x, y) = ( -3x
( -3x  - y)
- y)
A)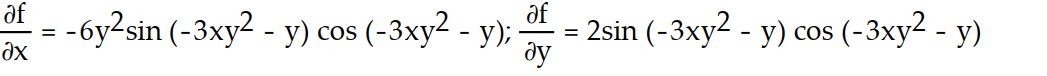
B)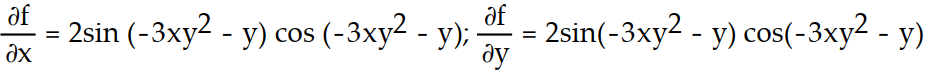
C)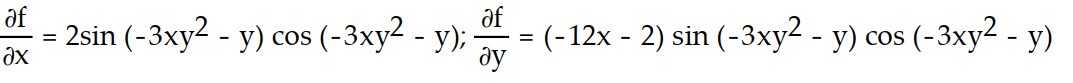
D)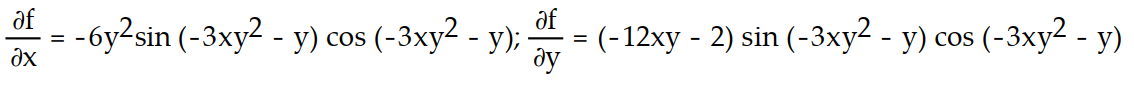
-f(x, y) =
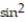 ( -3x
( -3x 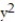 - y)
- y)A)
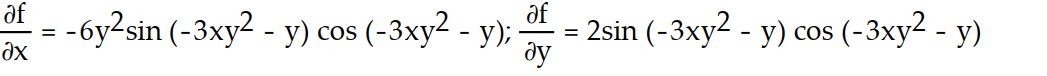
B)
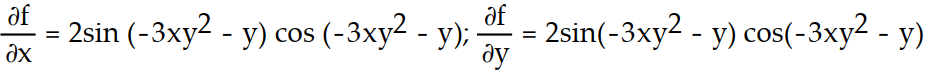
C)
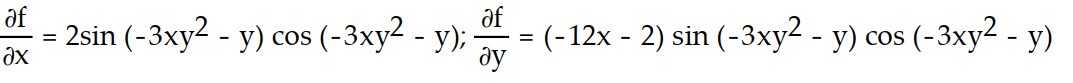
D)
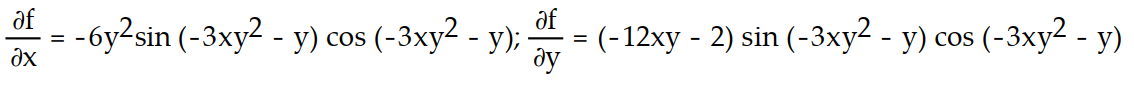

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
76
Find all the first order partial derivatives for the following function.
-f(x, y) = ln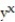
A)
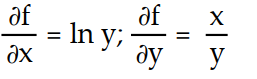
B)
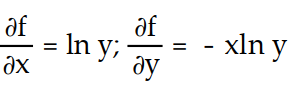
C)
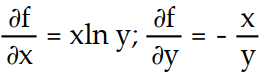
D)
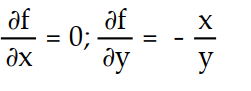
-f(x, y) = ln
A)
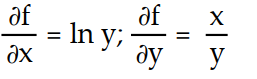
B)
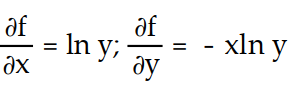
C)
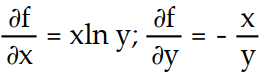
D)
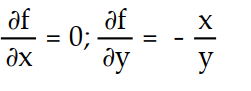

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
77
Find all the first order partial derivatives for the following function.
-f(x, y) =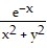
A)
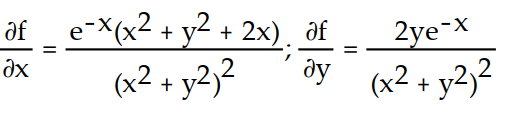
B)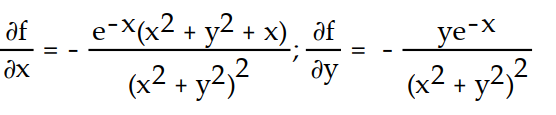
C)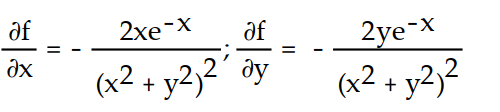
D)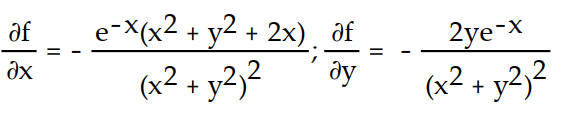
-f(x, y) =
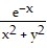
A)
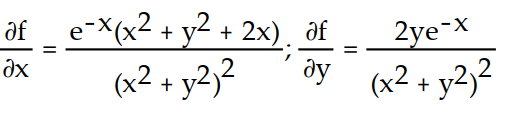
B)
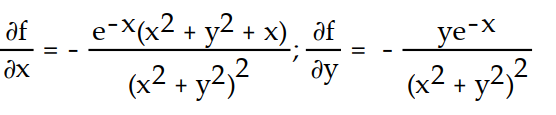
C)
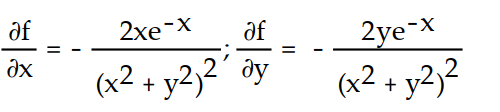
D)
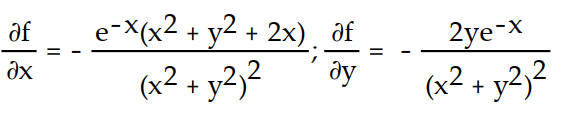

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
78
Find all the first order partial derivatives for the following function.
-f(x, y) =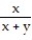
A)
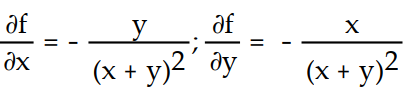
B)
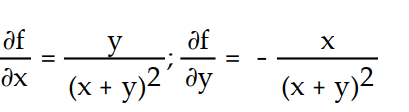
C)
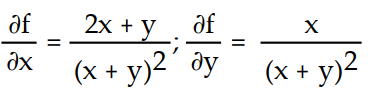
D)
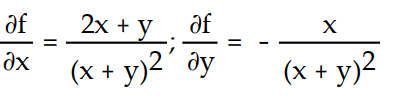
-f(x, y) =
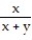
A)
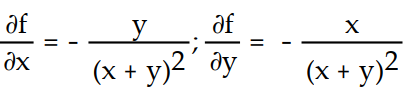
B)
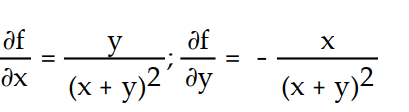
C)
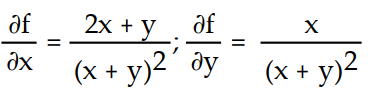
D)
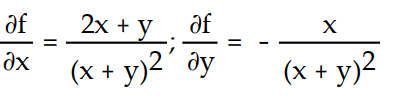

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
79
Find all the first order partial derivatives for the following function.
-f(x, y) = xy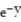
A)
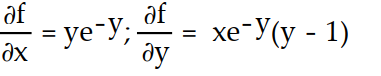
B)
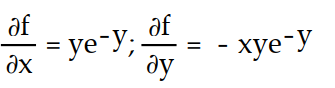
C)
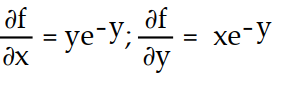
D)
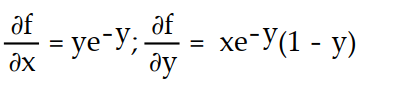
-f(x, y) = xy
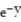
A)
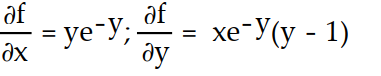
B)
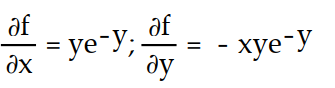
C)
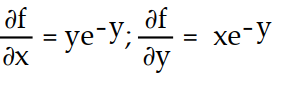
D)
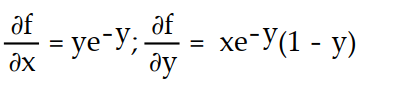

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck
80
Find all the first order partial derivatives for the following function.
-f(x, y) =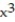 + 10
+ 10 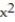 y - 2x
y - 2x 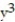
A)
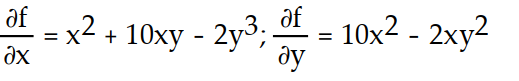
B)
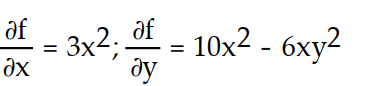
C)
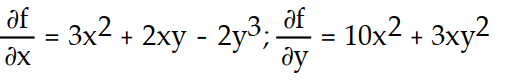
D)
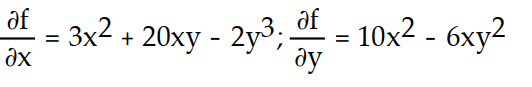
-f(x, y) =
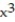 + 10
+ 10 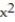 y - 2x
y - 2x 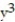
A)
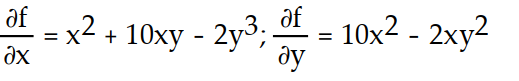
B)
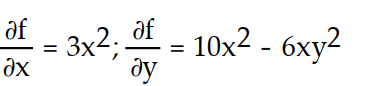
C)
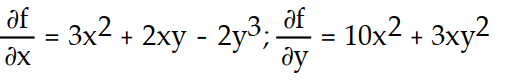
D)
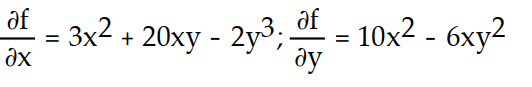

Unlock Deck
Unlock for access to all 229 flashcards in this deck.
Unlock Deck
k this deck


