Deck 14: Vector-Valued Functions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/83
Play
Full screen (f)
Deck 14: Vector-Valued Functions
1
Find a function r(t) that describes the line or line segment.
-The line through P(4, 9, 3) and Q(1, 6, 7)
A) r(t) =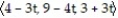
B) r(t) =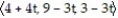
C) r(t) =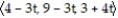
D) r(t) =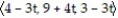
-The line through P(4, 9, 3) and Q(1, 6, 7)
A) r(t) =
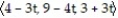
B) r(t) =
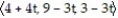
C) r(t) =
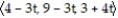
D) r(t) =
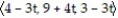
r(t) = 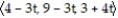
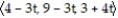
2
Find a function r(t) that describes the line or line segment.
-The line segment from P(2, 7, 3) to Q(3, 1, 1)
A) r(t) =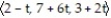 ; 1 t 2
; 1 t 2
B) r(t) =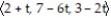 ; 1 t 2
; 1 t 2
C) r(t) =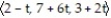 ; 0 t 1
; 0 t 1
D) r(t) =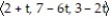 ; 0 t 1
; 0 t 1
-The line segment from P(2, 7, 3) to Q(3, 1, 1)
A) r(t) =
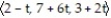 ; 1 t 2
; 1 t 2B) r(t) =
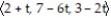 ; 1 t 2
; 1 t 2C) r(t) =
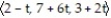 ; 0 t 1
; 0 t 1D) r(t) =
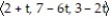 ; 0 t 1
; 0 t 1 r(t) = 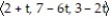 ; 0 t 1
; 0 t 1
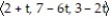 ; 0 t 1
; 0 t 1 3
Graph the curve described by the function, indicating the positive orientation.
-r(t) =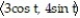 , for 0 t 2
, for 0 t 2
A)
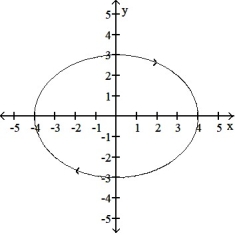
B)
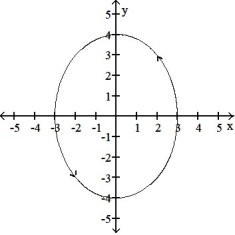
C)
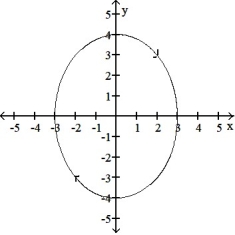
D)
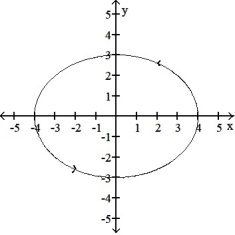
-r(t) =
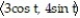 , for 0 t 2
, for 0 t 2 A)

B)

C)

D)


4
Graph the curve described by the function, indicating the positive orientation.
-r(t) = 2cos t i + 3j + 2 sin t k, for 0 t 2
A)
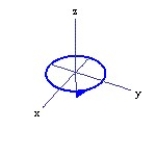
B)
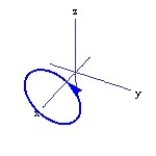
C)
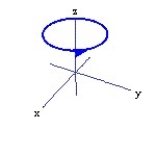
D)
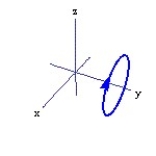
-r(t) = 2cos t i + 3j + 2 sin t k, for 0 t 2
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
5
Graph the curve described by the function. Use analysis to anticipate the shape of the curve before using a graphing utility.
-r(t) = 3 cos t i + 2 sin t j + cos 5t k, for 0 t 2
A)
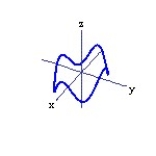
B)
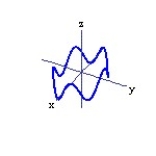
C)
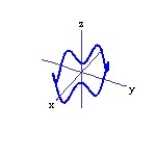
D)
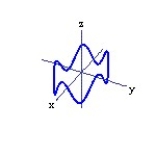
-r(t) = 3 cos t i + 2 sin t j + cos 5t k, for 0 t 2
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
6
Graph the curve described by the function. Use analysis to anticipate the shape of the curve before using a graphing utility.
-r(t) = cos 2t sin t i + sin 2t sin t j +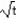 k, for 0 t 16
k, for 0 t 16
A)
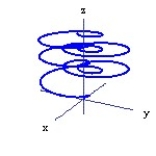
B)
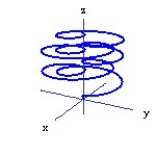
C)
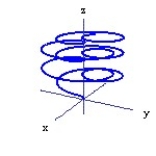
D)
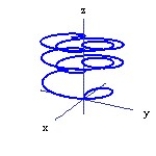
-r(t) = cos 2t sin t i + sin 2t sin t j +
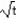 k, for 0 t 16
k, for 0 t 16A)

B)

C)

D)


Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
7
Evaluate the limit.
-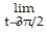 = ( 7 cos ti+ 6 sin tj)
= ( 7 cos ti+ 6 sin tj)
A) 7i
B) -6j
C) 6j
D) 7i - 6j
-
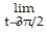 = ( 7 cos ti+ 6 sin tj)
= ( 7 cos ti+ 6 sin tj)A) 7i
B) -6j
C) 6j
D) 7i - 6j

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
8
Evaluate the limit.
-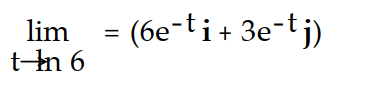
A)
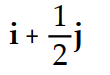
B)
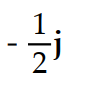
C)
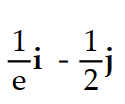
D)
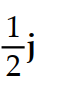
-
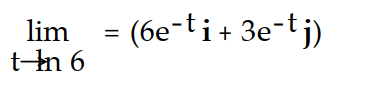
A)
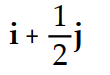
B)
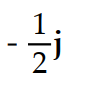
C)
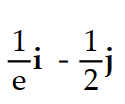
D)
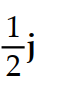

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
9
Find the domain of the vector-valued function.
-r(t) =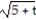 i +
i + 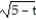 j
j
A) t 5
B) 5
5
C) < 5
< 5
D) t > 5
-r(t) =
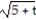 i +
i + 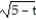 j
jA) t 5
B)
 5
5C)
 < 5
< 5D) t > 5

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
10
Find the domain of the vector-valued function.
-r(t) = sin 3t i +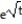 j
j
A) t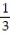
B) t 0
C) t > 3
D)All real numbers
-r(t) = sin 3t i +
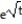 j
jA) t
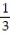
B) t 0
C) t > 3
D)All real numbers

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
11
Find a function r(t) that describes the curve where the surfaces intersect.
-z = 16; z =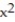 +
+ 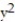
A) r(t) =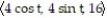
B) r(t) =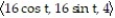
C) r(t) =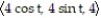
D) r(t) =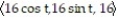
-z = 16; z =
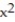 +
+ 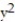
A) r(t) =
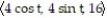
B) r(t) =
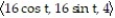
C) r(t) =
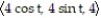
D) r(t) =
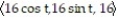

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
12
Find a function r(t) that describes the curve where the surfaces intersect.
-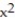 +
+ 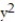 = 16; z = 2x + 3y
= 16; z = 2x + 3y
A) r(t) =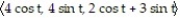
B) r(t) =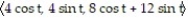
C) r(t) =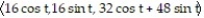
D) r(t) =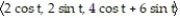
-
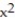 +
+ 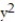 = 16; z = 2x + 3y
= 16; z = 2x + 3yA) r(t) =
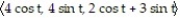
B) r(t) =
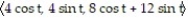
C) r(t) =
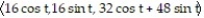
D) r(t) =
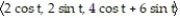

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
13
Verify that the curve r(t) lies on the surface. Give the name of the surface.
-r(t) = (2t cos t)i + (2t sin t)j + 2t k;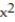 +
+ 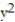 =
= 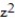
A)
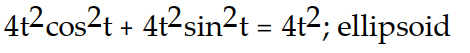
B)
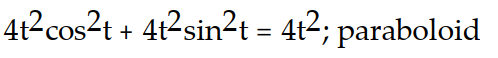
C)
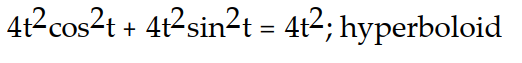
D)
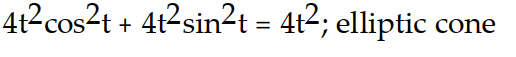
-r(t) = (2t cos t)i + (2t sin t)j + 2t k;
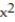 +
+ 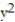 =
= 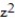
A)
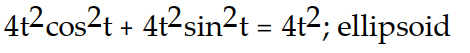
B)
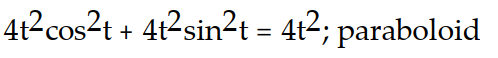
C)
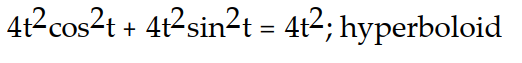
D)
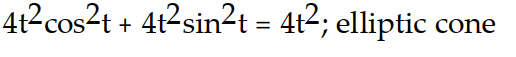

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
14
Verify that the curve r(t) lies on the surface. Give the name of the surface.
-r(t) =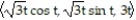 ; z=
; z= 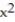 +
+ 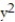
A)
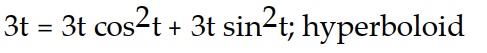
B)
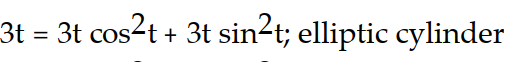
C)
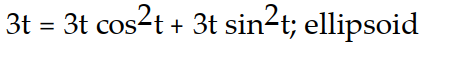
D)
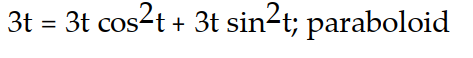
-r(t) =
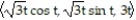 ; z=
; z= 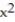 +
+ 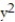
A)
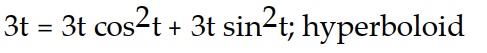
B)
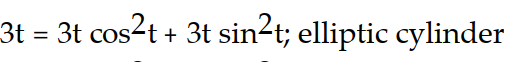
C)
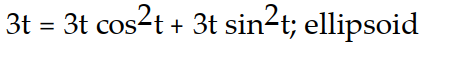
D)
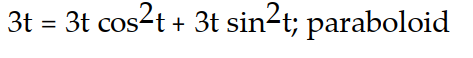

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
15
Differentiate the function.
-r(t) = ( -7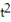 - 6)i +
- 6)i + 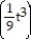 j
j
A)
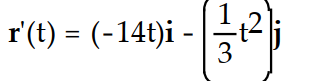
B)
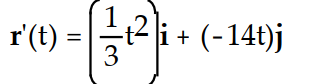
C)
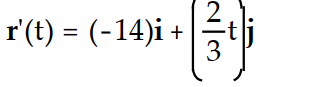
D)
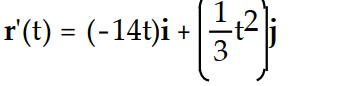
-r(t) = ( -7
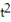 - 6)i +
- 6)i + 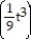 j
jA)
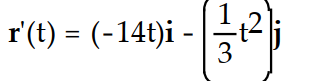
B)
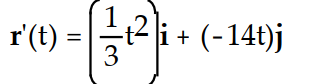
C)
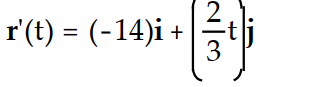
D)
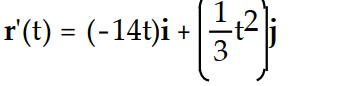

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
16
Differentiate the function.
-r(t) = (cot t)i + (csc t)j
A)
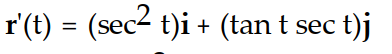
B)
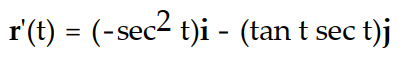
C)
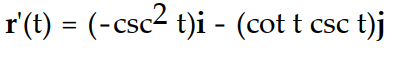
D)
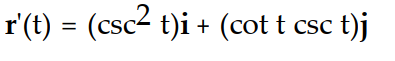
-r(t) = (cot t)i + (csc t)j
A)
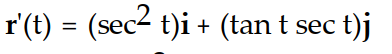
B)
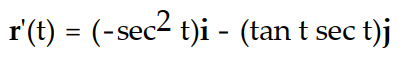
C)
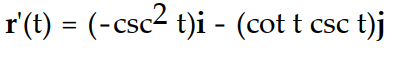
D)
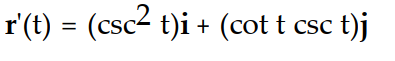

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
17
Find the unit tangent vector of the given curve.
-r(t) = 3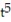 i - 12
i - 12 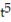 j + 4
j + 4 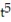 k
k
A)
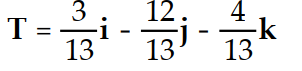
B)
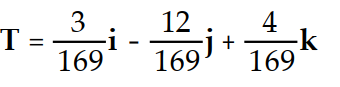
C)
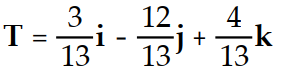
D)
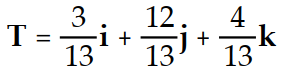
-r(t) = 3
 i - 12
i - 12 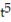 j + 4
j + 4 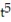 k
kA)
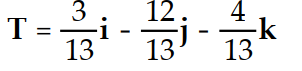
B)
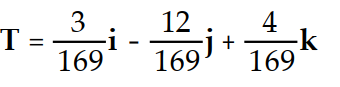
C)
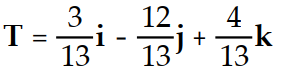
D)
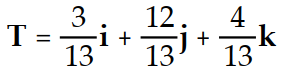

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
18
Find the unit tangent vector of the given curve.
-r(t) = ( 6 - 2t)i + (2t - 9)j + ( 9 + t)k
A)
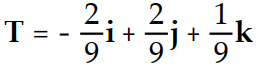
B)
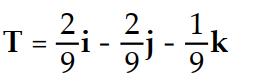
C)
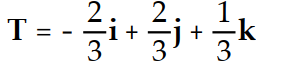
D)
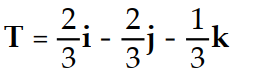
-r(t) = ( 6 - 2t)i + (2t - 9)j + ( 9 + t)k
A)
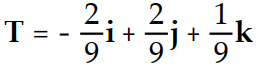
B)
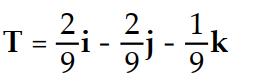
C)
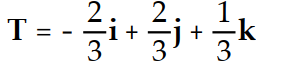
D)
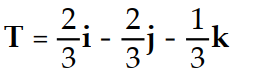

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
19
Find the unit tangent vector of the given curve.
-r(t) = ( 6 + 10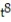 )i + ( 9 + 11
)i + ( 9 + 11 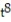 )j + ( 1 + 2
)j + ( 1 + 2 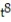 )k
)k
A)
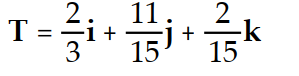
B)
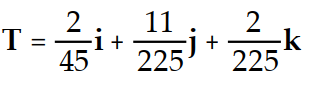
C) T = 10i + 11j + 2k
D)
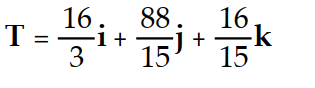
-r(t) = ( 6 + 10
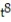 )i + ( 9 + 11
)i + ( 9 + 11 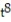 )j + ( 1 + 2
)j + ( 1 + 2 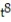 )k
)kA)
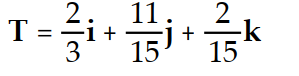
B)
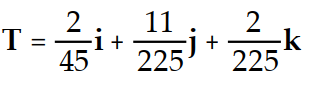
C) T = 10i + 11j + 2k
D)
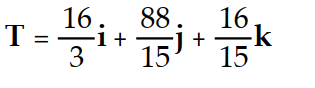

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
20
Find the unit tangent vector of the given curve.
-r(t) =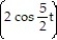 i +
i + 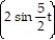 j - 12tk
j - 12tk
A)
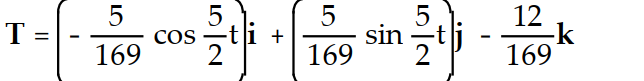
B)
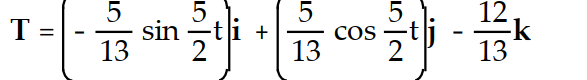
C)
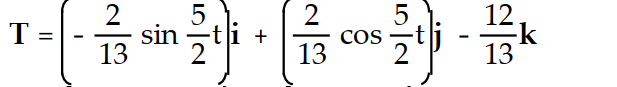
D)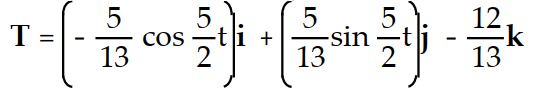
-r(t) =
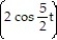 i +
i + 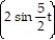 j - 12tk
j - 12tkA)
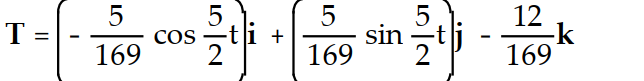
B)
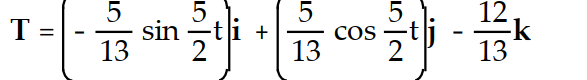
C)
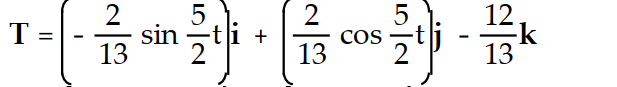
D)
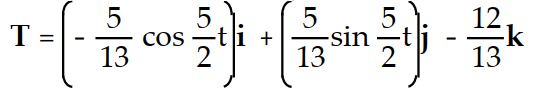

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
21
Find the unit tangent vector of the given curve.
-r(t) = ( 6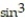 2t)i + ( 6
2t)i + ( 6 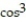 2t)j
2t)j
A) T = ( 6 sin 2t)i - ( 6 cos 2t)j
B) T = ( 36 sin 2t)i -( 36 cos 2t)j
C) T = (sin 2t)i - (cos 2t)j
D) T = ( 6 cos 2t)i - ( 6 sin 2t)j
-r(t) = ( 6
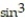 2t)i + ( 6
2t)i + ( 6 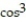 2t)j
2t)jA) T = ( 6 sin 2t)i - ( 6 cos 2t)j
B) T = ( 36 sin 2t)i -( 36 cos 2t)j
C) T = (sin 2t)i - (cos 2t)j
D) T = ( 6 cos 2t)i - ( 6 sin 2t)j

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
22
Find the unit tangent vector of the given curve.
-r(t) = ( 8t cos t - 8 sin t)j + ( 8t sin t + 8 cos t)k
A) T = (-8 sin t)j + ( 8 cos t)k
B) T = ( 8 cos t)j - ( 8 sin t)k
C) T = (-sin t)j + (cos t)k
D) T = -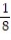 (sin t)j +
(sin t)j + 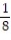 (cos t)k
(cos t)k
-r(t) = ( 8t cos t - 8 sin t)j + ( 8t sin t + 8 cos t)k
A) T = (-8 sin t)j + ( 8 cos t)k
B) T = ( 8 cos t)j - ( 8 sin t)k
C) T = (-sin t)j + (cos t)k
D) T = -
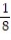 (sin t)j +
(sin t)j + 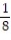 (cos t)k
(cos t)k
Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
23
Compute r''(t).
-r(t) = ( 2 cos t)i + ( 4 sin t)j
A) r''(t) = (-2 cos t)i + (-4 sin t)j
B) r''(t) = ( 2 cos t)i + ( 4 sin t)j
C) r''(t) = ( 2 sin t)i + ( 4 cos t)j
D) r''(t) = (-2 sin t)i + (-4 cos t)j
-r(t) = ( 2 cos t)i + ( 4 sin t)j
A) r''(t) = (-2 cos t)i + (-4 sin t)j
B) r''(t) = ( 2 cos t)i + ( 4 sin t)j
C) r''(t) = ( 2 sin t)i + ( 4 cos t)j
D) r''(t) = (-2 sin t)i + (-4 cos t)j

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
24
Compute r''(t).
-r(t) = (cos 2t)i + ( 3 sin t)j
A) r''(t) = (-2 cos 2t)i + ( 3 sin t)j
B) r''(t) = (-4 cos 2t)i + (-3 sin t)j
C) r''(t) = (-4 cos 2t)i + (-9 sin t)j
D) r''(t) = ( 4 cos 2t)i + (-3 sin t)j
-r(t) = (cos 2t)i + ( 3 sin t)j
A) r''(t) = (-2 cos 2t)i + ( 3 sin t)j
B) r''(t) = (-4 cos 2t)i + (-3 sin t)j
C) r''(t) = (-4 cos 2t)i + (-9 sin t)j
D) r''(t) = ( 4 cos 2t)i + (-3 sin t)j

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
25
Compute r''(t).
-r(t) = ( 3 ln( 6t))i + ( 2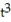 )j
)j
A)
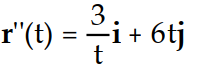
B)
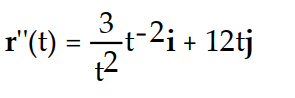
C)
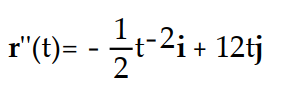
D)
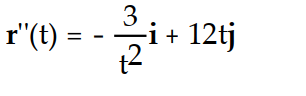
-r(t) = ( 3 ln( 6t))i + ( 2
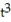 )j
)jA)
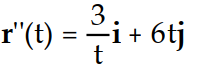
B)
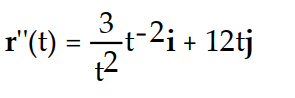
C)
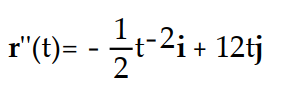
D)
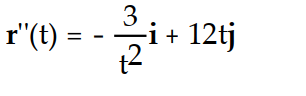

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
26
Evaluate the integral.
-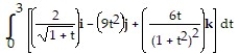
A)
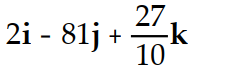
B)
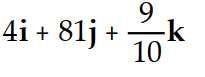
C)
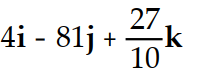
D)
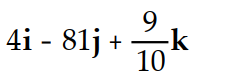
-
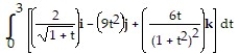
A)
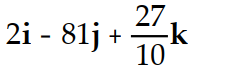
B)
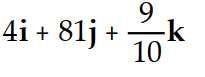
C)
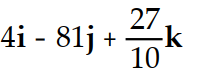
D)
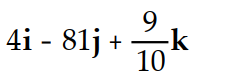

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
27
Evaluate the integral.
-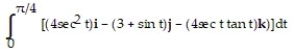
A)
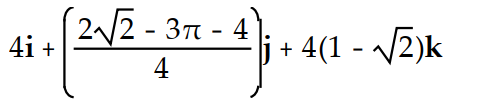
B)
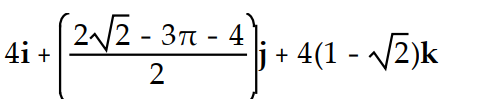
C)
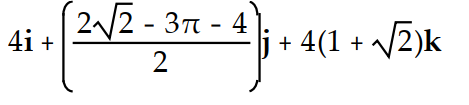
D)
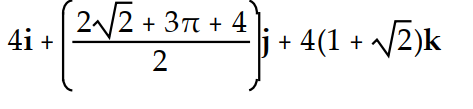
-
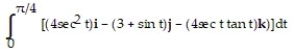
A)
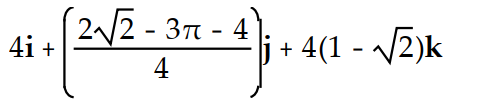
B)
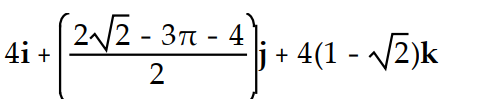
C)
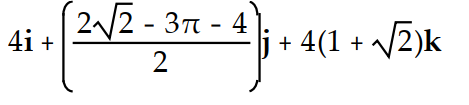
D)
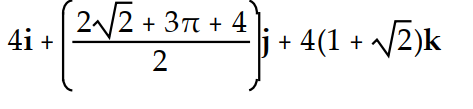

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
28
Evaluate the integral.
-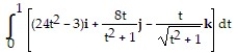
A) 11i + 4 ln 2j + (1 -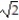 )k
)k
B) 5i + 4 ln 2j + (1 -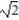 )k
)k
C) 11i + 4 ln 2j +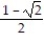 k
k
D) 11i + 4 ln 2j + (1 +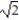 )k
)k
-
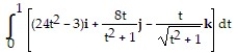
A) 11i + 4 ln 2j + (1 -
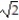 )k
)kB) 5i + 4 ln 2j + (1 -
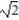 )k
)kC) 11i + 4 ln 2j +
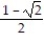 k
kD) 11i + 4 ln 2j + (1 +
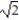 )k
)k
Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
29
Evaluate the integral.
-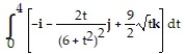
A) +4i +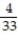 j + 24k
j + 24k
B) -4i -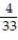 j - 24k
j - 24k
C) -4i -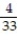 j + 24k
j + 24k
D) -4i +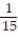 j + 24k
j + 24k
-
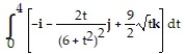
A) +4i +
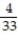 j + 24k
j + 24kB) -4i -
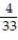 j - 24k
j - 24kC) -4i -
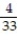 j + 24k
j + 24kD) -4i +
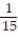 j + 24k
j + 24k
Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
30
Evaluate the integral.
-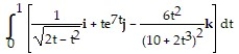
A)
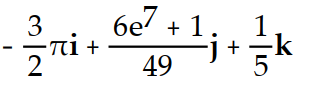
B)
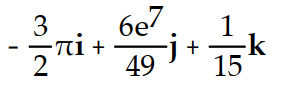
C)
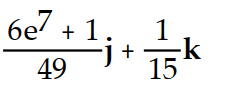
D)
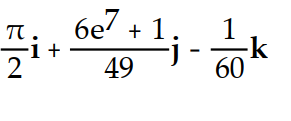
-
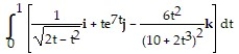
A)
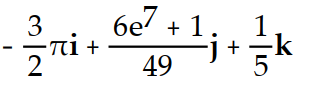
B)
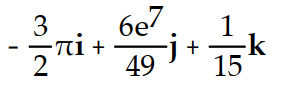
C)
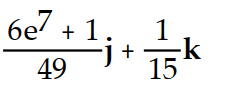
D)
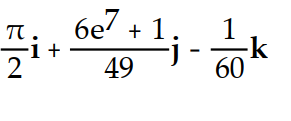

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
31
Evaluate the integral.
-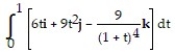
A) 3i + 3j -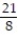 k
k
B) 3i - 3j - 11ee9522_3540_09d3_bdb6_ddd7428c17b9_TB9662_11 k
C) 6i - 6j + 3k
D) 6i + 6j - 3k
-
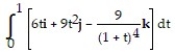
A) 3i + 3j -
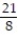 k
kB) 3i - 3j - 11ee9522_3540_09d3_bdb6_ddd7428c17b9_TB9662_11 k
C) 6i - 6j + 3k
D) 6i + 6j - 3k

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
32
Evaluate the integral.
-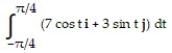
A) 7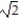 i
i
B) 0
C) 7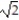 i + 3
i + 3 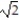 j
j
D) 3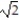 i
i
-
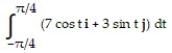
A) 7
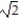 i
iB) 0
C) 7
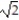 i + 3
i + 3 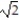 j
jD) 3
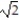 i
i
Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
33
Evaluate the integral.
-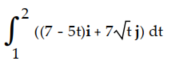
A)
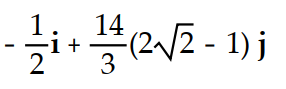
B) 7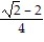 j
j
C)
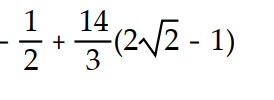
D)
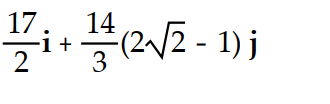
-
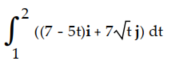
A)
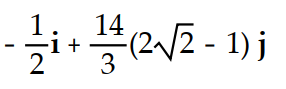
B) 7
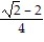 j
jC)
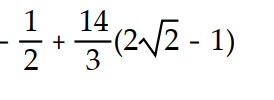
D)
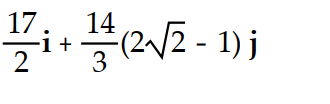

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
34
If r(t) is the position vector of a particle in the plane at time t, find the indicated vector.
-Find the velocity vector.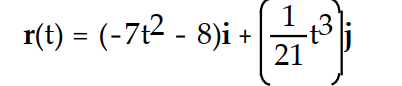
A)
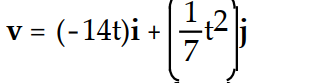
B)
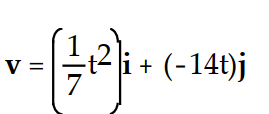
C)
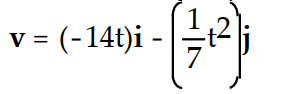
D)
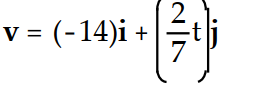
-Find the velocity vector.
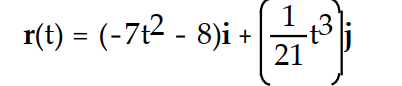
A)
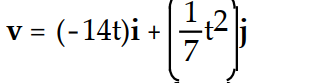
B)
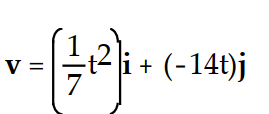
C)
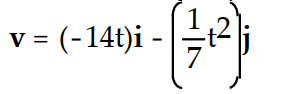
D)
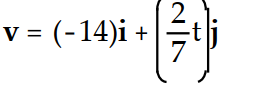

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
35
If r(t) is the position vector of a particle in the plane at time t, find the indicated vector.
-Find the acceleration vector. r(t) = ( 6 cos t)i + ( 8 sin t)j
A) a = (-6 sin t)i + (-8 cos t)j
B) a = ( 6 sin t)i + ( 8 cos t)j
C) a = ( 6 cos t)i + ( 8 sin t)j
D) a = (-6 cos t)i + (-8 sin t)j
-Find the acceleration vector. r(t) = ( 6 cos t)i + ( 8 sin t)j
A) a = (-6 sin t)i + (-8 cos t)j
B) a = ( 6 sin t)i + ( 8 cos t)j
C) a = ( 6 cos t)i + ( 8 sin t)j
D) a = (-6 cos t)i + (-8 sin t)j

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
36
If r(t) is the position vector of a particle in the plane at time t, find the indicated vector.
-Find the velocity vector. r(t) = (cot t)i + (csc t)j
A) v = (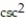 t)i + (cot t csc t)j
t)i + (cot t csc t)j
B) v = (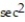 t)i + (tan t sec t)j
t)i + (tan t sec t)j
C) v = (-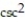 t)i - (cot t csc t)j
t)i - (cot t csc t)j
D) v = (-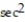 t)i - (tan t sec t)j
t)i - (tan t sec t)j
-Find the velocity vector. r(t) = (cot t)i + (csc t)j
A) v = (
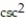 t)i + (cot t csc t)j
t)i + (cot t csc t)jB) v = (
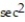 t)i + (tan t sec t)j
t)i + (tan t sec t)jC) v = (-
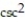 t)i - (cot t csc t)j
t)i - (cot t csc t)jD) v = (-
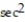 t)i - (tan t sec t)j
t)i - (tan t sec t)j
Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
37
If r(t) is the position vector of a particle in the plane at time t, find the indicated vector.
-Find the acceleration vector. r(t) = ( 7 ln( 5t))i + ( 3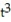 )j
)j
A)
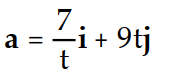
B)
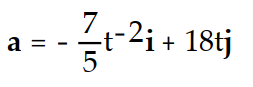
C)
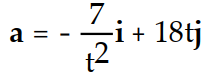
D)
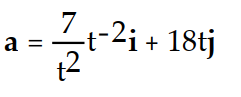
-Find the acceleration vector. r(t) = ( 7 ln( 5t))i + ( 3
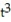 )j
)jA)
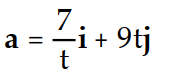
B)
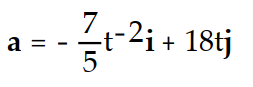
C)
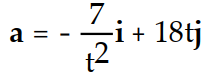
D)
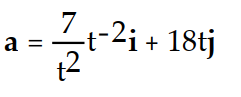

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
38
The position vector of a particle is r(t). Find the requested vector.
-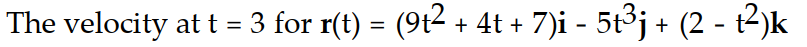
A) v( 3) = 58i - 135j - 6k
B) v( 3) = 31i - 45j - 3k
C) v( 3) = 58i + 135j + 6k
D) v( 3) = 50i - 135j - 6k
-
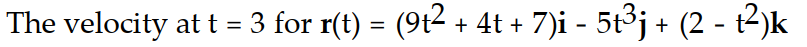
A) v( 3) = 58i - 135j - 6k
B) v( 3) = 31i - 45j - 3k
C) v( 3) = 58i + 135j + 6k
D) v( 3) = 50i - 135j - 6k

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
39
The position vector of a particle is r(t). Find the requested vector.
-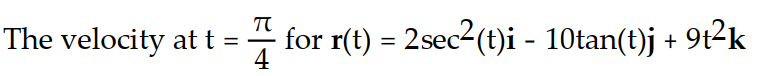
A)
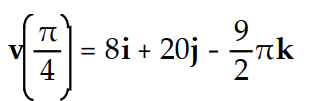
B)
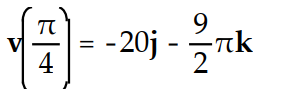
C)
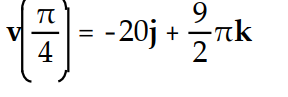
D)
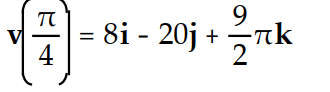
-
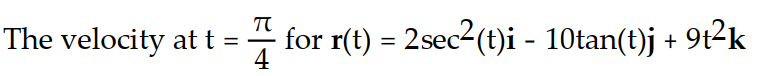
A)
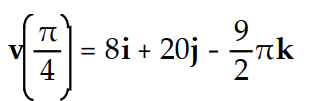
B)
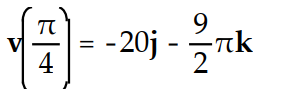
C)
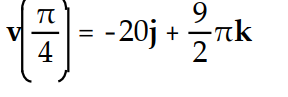
D)
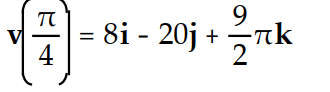

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
40
The position vector of a particle is r(t). Find the requested vector.
-The velocity at t = 0 for r(t) = cos( 2t)i + 7ln(t - 3)j -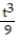 k
k
A) v(0) =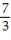 j
j
B) v(0) = -2i -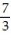 j
j
C) v(0) = -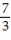 j
j
D) v(0) = 2i -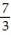 j
j
-The velocity at t = 0 for r(t) = cos( 2t)i + 7ln(t - 3)j -
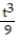 k
kA) v(0) =
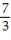 j
jB) v(0) = -2i -
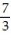 j
jC) v(0) = -
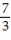 j
jD) v(0) = 2i -
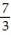 j
j
Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
41
The position vector of a particle is r(t). Find the requested vector.
-The velocity at t = 3 for r(t) = ( 8 - 4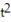 )i + ( 6t + 7)j -
)i + ( 6t + 7)j - 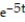 k
k
A)v( 3) = -24i + 6j + 5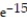 k
k
B) v( 3) = -24i + 6j - 5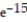 k
k
C) v( 3) = -12i +6j + 5 k
k
D) v( 3) = 24i + 6j + 5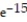 k
k
-The velocity at t = 3 for r(t) = ( 8 - 4
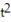 )i + ( 6t + 7)j -
)i + ( 6t + 7)j - 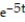 k
kA)v( 3) = -24i + 6j + 5
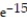 k
kB) v( 3) = -24i + 6j - 5
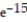 k
kC) v( 3) = -12i +6j + 5
 k
kD) v( 3) = 24i + 6j + 5
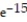 k
k
Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
42
The position vector of a particle is r(t). Find the requested vector.
-The velocity at t = 0 for r(t) = ln(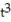 - 5
- 5 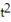 + 3)i -
+ 3)i - 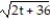 j - 5cos(t)k
j - 5cos(t)k
A) v( 0) =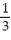 i -
i - 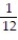 j + 5k
j + 5k
B) v( 0) =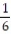 j
j
C) v( 0) =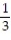 i -
i - 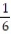 j
j
D) v( 0) = -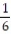 j
j
-The velocity at t = 0 for r(t) = ln(
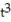 - 5
- 5 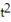 + 3)i -
+ 3)i - 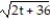 j - 5cos(t)k
j - 5cos(t)kA) v( 0) =
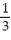 i -
i - 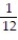 j + 5k
j + 5kB) v( 0) =
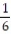 j
jC) v( 0) =
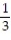 i -
i - 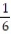 j
jD) v( 0) = -
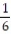 j
j
Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
43
The position vector of a particle is r(t). Find the requested vector.
-The acceleration at t =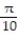 for r(t) = ( 9 sin 5t)i - ( 10 cos 5t)j + ( 2 csc 5t)k
for r(t) = ( 9 sin 5t)i - ( 10 cos 5t)j + ( 2 csc 5t)k
A) a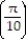 = -225i - 50k
= -225i - 50k
B) a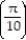 = 225i + 50k
= 225i + 50k
C) a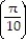 = -225i + 50k
= -225i + 50k
D) a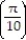 = 250j + 50k
= 250j + 50k
-The acceleration at t =
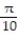 for r(t) = ( 9 sin 5t)i - ( 10 cos 5t)j + ( 2 csc 5t)k
for r(t) = ( 9 sin 5t)i - ( 10 cos 5t)j + ( 2 csc 5t)kA) a
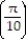 = -225i - 50k
= -225i - 50kB) a
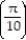 = 225i + 50k
= 225i + 50kC) a
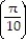 = -225i + 50k
= -225i + 50kD) a
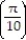 = 250j + 50k
= 250j + 50k
Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
44
The position vector of a particle is r(t). Find the requested vector.
-The acceleration at t = 2 for r(t) = ( 7t - 3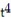 )i + ( 10 - t)j + ( 2
)i + ( 10 - t)j + ( 2 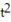 - 3t)k
- 3t)k
A) a( 2) = -144i - j + 4k
B) a( 2) = 144i + 4k
C) a( 2) = -144i + 4k
D) a( 2) = -36i + 4k
-The acceleration at t = 2 for r(t) = ( 7t - 3
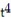 )i + ( 10 - t)j + ( 2
)i + ( 10 - t)j + ( 2 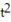 - 3t)k
- 3t)kA) a( 2) = -144i - j + 4k
B) a( 2) = 144i + 4k
C) a( 2) = -144i + 4k
D) a( 2) = -36i + 4k

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
45
The position vector of a particle is r(t). Find the requested vector.
-The acceleration at t = 1 for r(t) =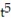 i + 2ln
i + 2ln 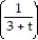 j +
j + 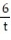 k
k
A) a(1) = 20i + 2j + 12k
B) a(1) = 20i +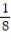 j - 12k
j - 12k
C) a(1) = 20i - 2j - 12k
D) a(1) = 20i +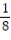 j + 12k
j + 12k
-The acceleration at t = 1 for r(t) =
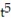 i + 2ln
i + 2ln 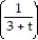 j +
j + 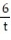 k
kA) a(1) = 20i + 2j + 12k
B) a(1) = 20i +
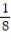 j - 12k
j - 12kC) a(1) = 20i - 2j - 12k
D) a(1) = 20i +
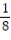 j + 12k
j + 12k
Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
46
The position vector of a particle is r(t). Find the requested vector.
-The acceleration at t =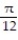 for r(t) =
for r(t) = 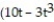 )i + 2tan( 3t)j +
)i + 2tan( 3t)j + 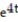 k
k
A)
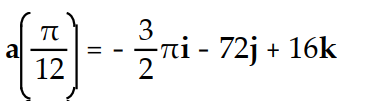
B)
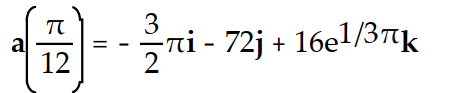
C)
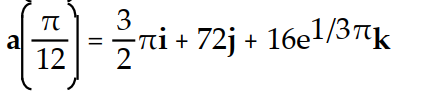
D)
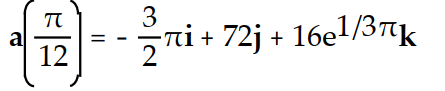
-The acceleration at t =
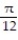 for r(t) =
for r(t) = 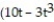 )i + 2tan( 3t)j +
)i + 2tan( 3t)j + 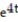 k
kA)
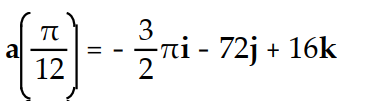
B)
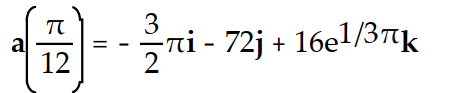
C)
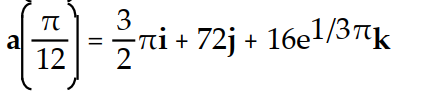
D)
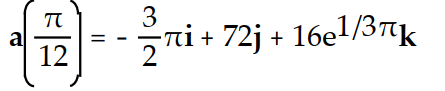

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
47
The position vector of a particle is r(t). Find the requested vector.
-The acceleration at t = 0 for r(t) =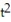 i + ( 10
i + ( 10 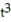 - 2)j +
- 2)j + 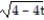 k
k
A) a(0) = 2i - 2k
B) a(0) = 2i -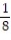 k
k
C)a(0) = 2i -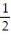 k
k
D) a(0) = 2i +
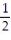 k
k
-The acceleration at t = 0 for r(t) =
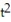 i + ( 10
i + ( 10 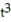 - 2)j +
- 2)j + 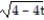 k
kA) a(0) = 2i - 2k
B) a(0) = 2i -
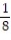 k
kC)a(0) = 2i -
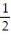 k
kD) a(0) = 2i +
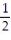 k
k
Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
48
Solve the problem. Assume the x-axis is horizontal, the positive y-axis is vertical (opposite g), the ground is horizontal, and only the gravitational force acts on the objects
-A projectile is launched from the origin at an angle of radians to the horizontal and an initial speed of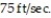 Find the position function r(t) for this projectile.
Find the position function r(t) for this projectile.
A) r(t) = ( 75t cos - 32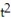 )i + ( 75t sin )j
)i + ( 75t sin )j
B) r(t) = ( 75t sin )i + ( 75t cos - 16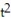 )j
)j
C) r(t) = ( 75t cos )i + ( 75t sin - 16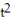 )j
)j
D) r(t) = ( 75t sin - 16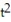 )i + ( 75t cos )j
)i + ( 75t cos )j
-A projectile is launched from the origin at an angle of radians to the horizontal and an initial speed of
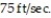 Find the position function r(t) for this projectile.
Find the position function r(t) for this projectile.A) r(t) = ( 75t cos - 32
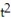 )i + ( 75t sin )j
)i + ( 75t sin )jB) r(t) = ( 75t sin )i + ( 75t cos - 16
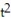 )j
)jC) r(t) = ( 75t cos )i + ( 75t sin - 16
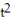 )j
)jD) r(t) = ( 75t sin - 16
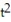 )i + ( 75t cos )j
)i + ( 75t cos )j
Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
49
Solve the problem. Assume the x-axis is horizontal, the positive y-axis is vertical (opposite g), the ground is horizontal, and only the gravitational force acts on the objects
-A projectile is fired at a speed of 800 m/sec at an angle of 34°. How long will it take to get 20 km downrange? Round your answer to the nearest whole number.
A) 32 sec
B) It will never get that far downrange.
C) 30 sec
D) 28 sec
-A projectile is fired at a speed of 800 m/sec at an angle of 34°. How long will it take to get 20 km downrange? Round your answer to the nearest whole number.
A) 32 sec
B) It will never get that far downrange.
C) 30 sec
D) 28 sec

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
50
Solve the problem. Assume the x-axis is horizontal, the positive y-axis is vertical (opposite g), the ground is horizontal, and only the gravitational force acts on the objects
-A projectile is fired with an initial speed of 585 m/sec at an angle of 45°. What is the greatest height reached by the projectile? Round your answer to the nearest tenth.
A) 85,556.3 m
B) 8730.2 m
C) 34,920.9 m
D) 84.4 m
-A projectile is fired with an initial speed of 585 m/sec at an angle of 45°. What is the greatest height reached by the projectile? Round your answer to the nearest tenth.
A) 85,556.3 m
B) 8730.2 m
C) 34,920.9 m
D) 84.4 m

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
51
Find the length of the indicated portion of the trajectory.
-r(t) = ( 2cos t)i + ( 2sin t)j + 5tk, 0 t /2
A)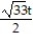
B)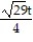
C)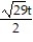
D)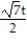
-r(t) = ( 2cos t)i + ( 2sin t)j + 5tk, 0 t /2
A)
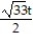
B)
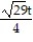
C)
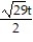
D)
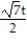

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
52
Find the length of the indicated portion of the trajectory.
-r(t) = ( cos t)i + (
cos t)i + (  sin t)j +
sin t)j + 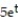 k, -ln 2 t 0
k, -ln 2 t 0
A)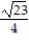
B)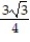
C)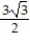
D)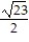
-r(t) = (
 cos t)i + (
cos t)i + (  sin t)j +
sin t)j + 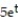 k, -ln 2 t 0
k, -ln 2 t 0A)
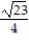
B)
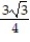
C)
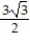
D)
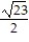

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
53
Find the length of the indicated portion of the trajectory.
-r(t) = (1 + 5t)i + (1 + 8t)j + ( 2 - 2t)k, -1 t 0
A)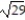
B) 2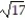
C)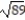
D)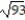
-r(t) = (1 + 5t)i + (1 + 8t)j + ( 2 - 2t)k, -1 t 0
A)
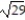
B) 2
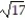
C)
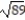
D)

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
54
Find the length of the indicated portion of the trajectory.
-r(t) = ( 2 + 2t)i + ( 3 + 3t)j + ( 3 - 6t)k, -1 t 0
A) 8
B) 5
C) 9
D) 7
-r(t) = ( 2 + 2t)i + ( 3 + 3t)j + ( 3 - 6t)k, -1 t 0
A) 8
B) 5
C) 9
D) 7

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
55
Write the word or phrase that best completes each statement or answers the question. Provide an appropriate response
-Show that the arc length of one petal of the rose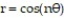 is given by
is given by
2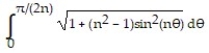 and use this formula to help make a conjecture about the limit of such arc lengths as
and use this formula to help make a conjecture about the limit of such arc lengths as 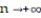
-Show that the arc length of one petal of the rose
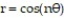 is given by
is given by2
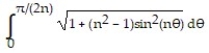 and use this formula to help make a conjecture about the limit of such arc lengths as
and use this formula to help make a conjecture about the limit of such arc lengths as 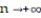

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
56
Find the curvature of the curve r(t).
-r(t) = ( 8 + ln(sec t))i + ( 3 + t)k, - /2 < t < /2
A)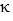 = cos t
= cos t
B) 11ee983b_f671_a800_a6de_a1c79ef1661c_TB9662_11= sin t
C) 11ee983b_f671_a800_a6de_a1c79ef1661c_TB9662_11 = 1-cos t
D) 11ee983b_f671_a800_a6de_a1c79ef1661c_TB9662_11= -cos t
-r(t) = ( 8 + ln(sec t))i + ( 3 + t)k, - /2 < t < /2
A)
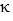 = cos t
= cos tB) 11ee983b_f671_a800_a6de_a1c79ef1661c_TB9662_11= sin t
C) 11ee983b_f671_a800_a6de_a1c79ef1661c_TB9662_11 = 1-cos t
D) 11ee983b_f671_a800_a6de_a1c79ef1661c_TB9662_11= -cos t

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
57
Find the curvature of the curve r(t).
-r(t) = ( 10 + 6 cos 9t) i - ( 2 + 6 sin 9t)j + 2k
A)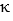 = 6
= 6
B) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =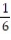
C) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =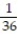
D) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =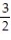
-r(t) = ( 10 + 6 cos 9t) i - ( 2 + 6 sin 9t)j + 2k
A)
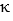 = 6
= 6B) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =
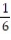
C) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =
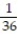
D) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =
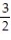

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
58
Find the curvature of the curve r(t).
-r(t) = ( 7 + cos 8t - sin 8t)i + ( 5 + sin 8t + cos 8t)j + 6k
A)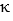 =
= 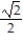
B) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 = 4
C) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11= 4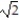
D) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =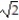
-r(t) = ( 7 + cos 8t - sin 8t)i + ( 5 + sin 8t + cos 8t)j + 6k
A)
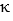 =
= 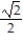
B) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 = 4
C) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11= 4
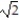
D) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
59
Find the curvature of the curve r(t).
-r(t) = ( 7t + 3)i - 7j + ( 4 -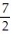
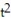 )k
)k
A)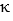 =
= 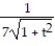
B) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 = 7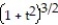
C)11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 = 7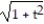
D) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =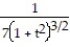
-r(t) = ( 7t + 3)i - 7j + ( 4 -
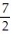
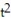 )k
)kA)
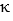 =
= 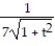
B) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 = 7
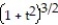
C)11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 = 7
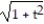
D) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =
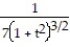

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
60
Find the curvature of the space curve.
-r(t) = 12ti +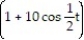 j +
j + 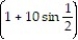 k
k
A)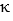 =
= 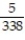
B) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =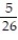
C) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =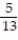
D) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =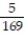
-r(t) = 12ti +
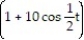 j +
j + 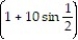 k
kA)
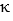 =
= 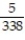
B) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =
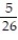
C) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =
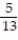
D) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =
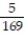

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
61
Find the curvature of the space curve.
-r(t) = (t + 5)i + 8j + (ln(sec t) + 1)k
A) = cos t
= cos t
B) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 = sec t
C) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 = sin t
D) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11= csc t
-r(t) = (t + 5)i + 8j + (ln(sec t) + 1)k
A)
 = cos t
= cos tB) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 = sec t
C) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 = sin t
D) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11= csc t

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
62
Find the curvature of the space curve.
-r(t) = -10i + (t + 5)j +(ln(cos t) + 4)k
A)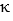 = sin t
= sin t
B) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 = csc t
C) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 = sec t
D) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 = cos t
-r(t) = -10i + (t + 5)j +(ln(cos t) + 4)k
A)
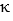 = sin t
= sin tB) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 = csc t
C) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 = sec t
D) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 = cos t

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
63
Find the curvature of the space curve.
-r(t) = -10i + ( 6 + 2t)j + (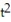 + 2)k
+ 2)k
A)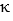 = -
= - 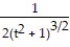
B) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11=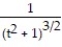
C) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =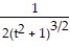
D) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =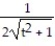
-r(t) = -10i + ( 6 + 2t)j + (
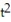 + 2)k
+ 2)kA)
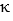 = -
= - 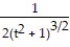
B) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11=
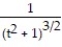
C) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =
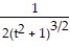
D) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =
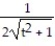

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
64
Find the curvature of the space curve.
-r(t) = ( 9 t sin t + 9 cos t)i + 9j + ( 9t cos t - 9 sin t)k
A)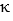 = -
= - 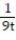
B) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 = 9t
C) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =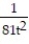
D) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =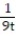
-r(t) = ( 9 t sin t + 9 cos t)i + 9j + ( 9t cos t - 9 sin t)k
A)
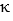 = -
= - 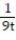
B) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 = 9t
C) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =
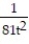
D) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =
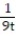

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
65
Find the curvature of the space curve.
-r(t) = ti + (sinh t)j + (cosh t)k
A)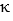 =
= 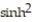 t
t
B) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =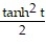
C) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =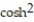 t
t
D) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =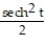
-r(t) = ti + (sinh t)j + (cosh t)k
A)
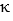 =
= 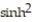 t
tB) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =
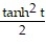
C) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =
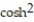 t
tD) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =
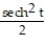

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
66
Find the curvature of the space curve.
-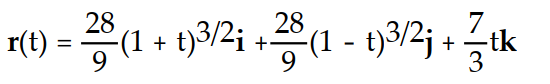
A)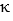 =
= 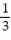
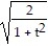
B) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =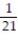
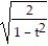
C) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =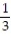
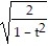
D) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =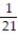
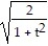
-
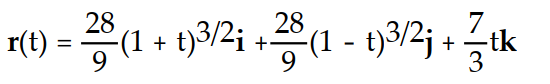
A)
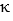 =
= 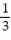
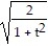
B) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =
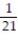
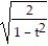
C) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =
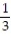
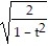
D) 11ee983c_18fb_aab1_a6de_e7ae6ccbb311_TB9662_11 =
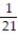
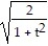

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
67
Find the unit tangent vector T and the principal unit normal vector N.
-r(t) =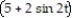 i +
i +  j + 3tk
j + 3tk
A)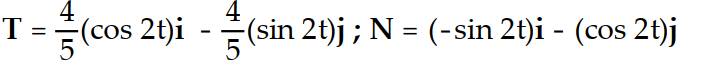
B)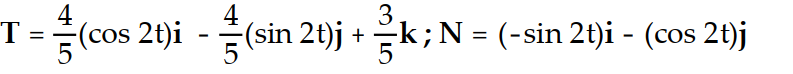
C)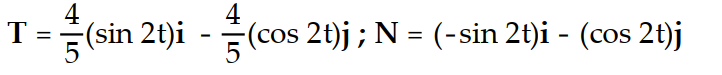
D)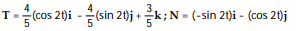
-r(t) =
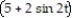 i +
i +  j + 3tk
j + 3tkA)
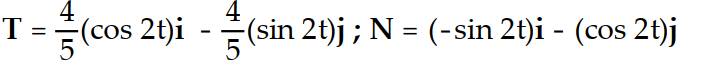
B)
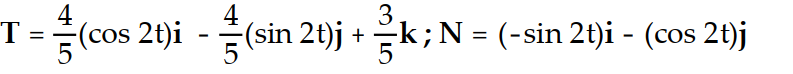
C)
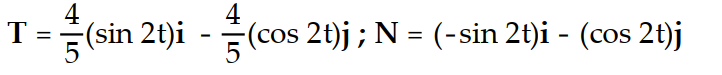
D)
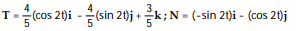

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
68
Find the unit tangent vector T and the principal unit normal vector N.
-r(t) = ( 3 + t)i + ( 7 + ln(sec t))j - 3k, - /2 < t < /2
A) T = (-cos t)i - (sin t)j; N = (-cos t)i + (sin t)j
B) T = (cos t)i + (sin t)j; N = (- sin t)i + (cos t)j
C)T = (cos t)i - (sin t)j; N = (-sin t)i - (cos t)j
D) T = (-cos t)i - (sin t)j; N = (sin t)i - (cos t)j
-r(t) = ( 3 + t)i + ( 7 + ln(sec t))j - 3k, - /2 < t < /2
A) T = (-cos t)i - (sin t)j; N = (-cos t)i + (sin t)j
B) T = (cos t)i + (sin t)j; N = (- sin t)i + (cos t)j
C)T = (cos t)i - (sin t)j; N = (-sin t)i - (cos t)j
D) T = (-cos t)i - (sin t)j; N = (sin t)i - (cos t)j

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
69
Find the unit tangent vector T and the principal unit normal vector N.
-r(t) = (ln(cos t) + 9)i + 9j + ( 10 + t )k, - /2 < t < /2
A) T = (sin t)i - (cos t)k; N = (cos t)i - (sin t)k;
B) T = (sin t)i + (cos t)k; N = (cos t)i - (sin t)k
C) T = (-sin t)i + (cos t)k; N = (-cos t)i + (sin t)k
D) T = (-sin t)i + (cos t)k; N = (-cos t)i - (sin t)k
-r(t) = (ln(cos t) + 9)i + 9j + ( 10 + t )k, - /2 < t < /2
A) T = (sin t)i - (cos t)k; N = (cos t)i - (sin t)k;
B) T = (sin t)i + (cos t)k; N = (cos t)i - (sin t)k
C) T = (-sin t)i + (cos t)k; N = (-cos t)i + (sin t)k
D) T = (-sin t)i + (cos t)k; N = (-cos t)i - (sin t)k

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
70
Find the unit tangent vector T and the principal unit normal vector N.
-r(t) = (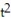 - 8)i + (2t - 6)j + 5k
- 8)i + (2t - 6)j + 5k
A)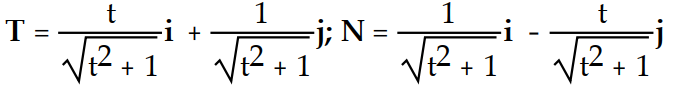
B)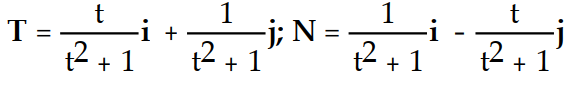
C)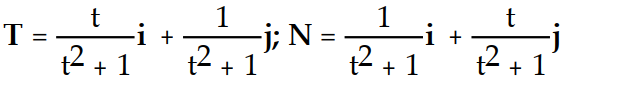
D)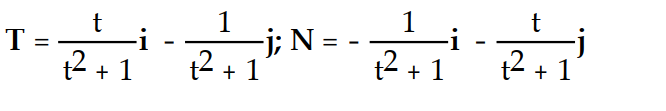
-r(t) = (
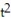 - 8)i + (2t - 6)j + 5k
- 8)i + (2t - 6)j + 5kA)
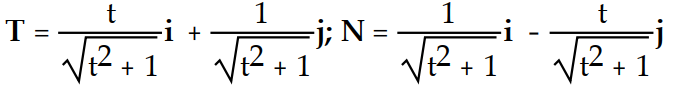
B)
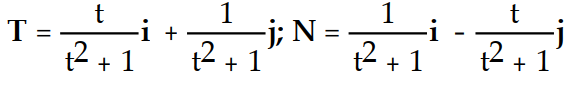
C)
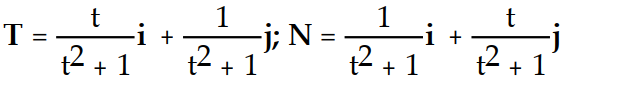
D)
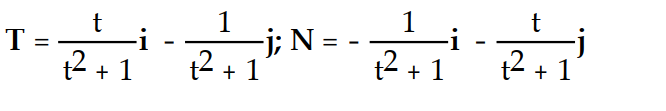

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
71
Find the unit tangent vector T and the principal unit normal vector N.
-r(t) = ( 7t sin t + 7cos t)i + ( 7t cos t - 7 sin t)j - 4k
A) T = (cos t)i + (sin t)j; N = (-sin t)i + (cos t)j
B) T = (-cos t)i - (sin t)j; N = (sin t)i - (cos t)j
C) T = (cos t)i - (sin t)j; N = (-sin t)i - (cos t)j
D) T = (-cos t)i - (sin t)j; N = (sin t)i + (cos t)j
-r(t) = ( 7t sin t + 7cos t)i + ( 7t cos t - 7 sin t)j - 4k
A) T = (cos t)i + (sin t)j; N = (-sin t)i + (cos t)j
B) T = (-cos t)i - (sin t)j; N = (sin t)i - (cos t)j
C) T = (cos t)i - (sin t)j; N = (-sin t)i - (cos t)j
D) T = (-cos t)i - (sin t)j; N = (sin t)i + (cos t)j

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
72
Find the unit tangent vector T and the principal unit normal vector N.
-r(t) = (cosh t)i + (sinh t)j + tk
A)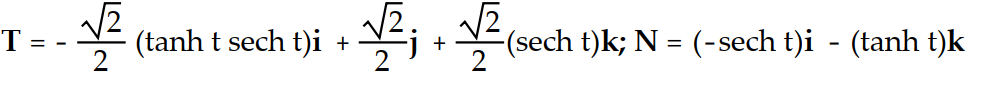
B)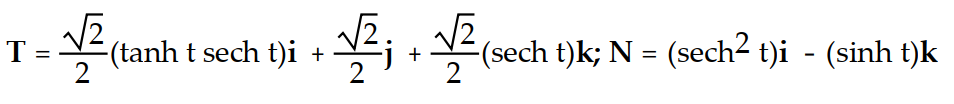
C)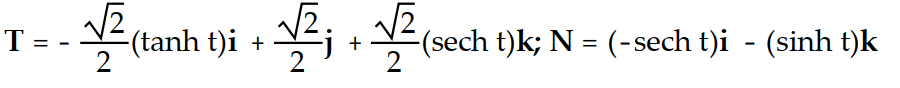
D)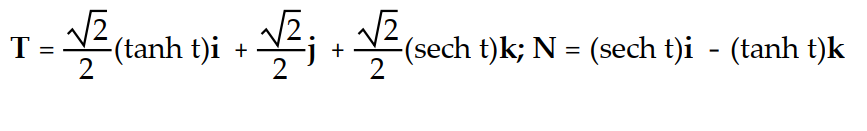
-r(t) = (cosh t)i + (sinh t)j + tk
A)
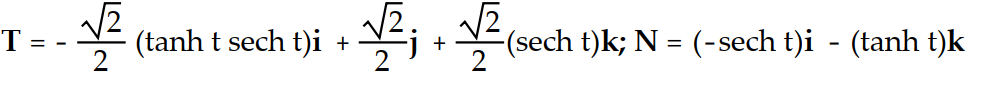
B)
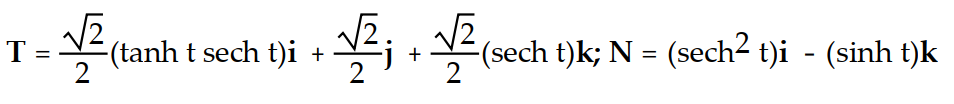
C)
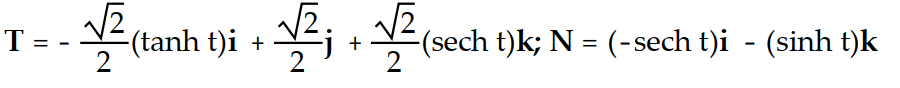
D)
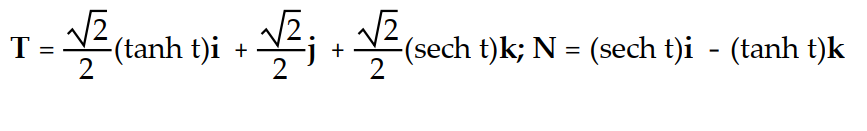

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
73
Find the unit tangent vector T and the principal unit normal vector N.
-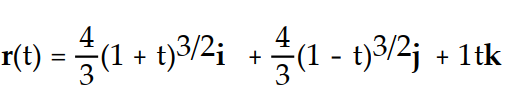
A)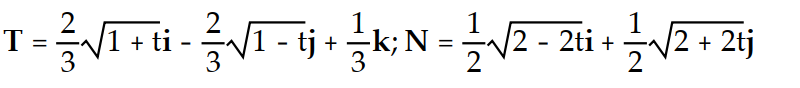
B)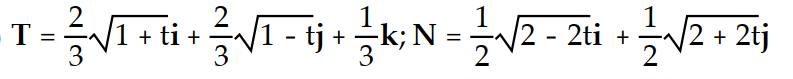
C)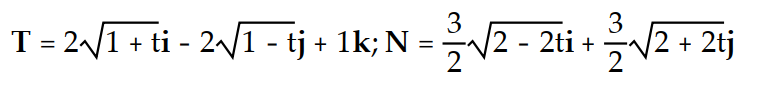
D)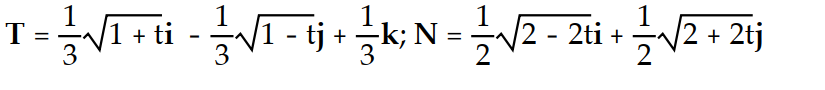
-
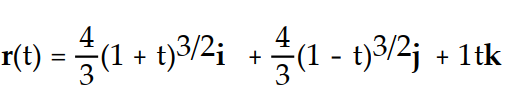
A)
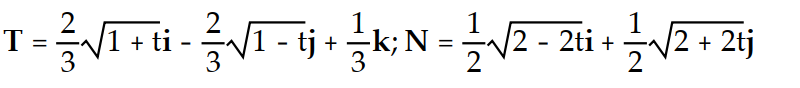
B)
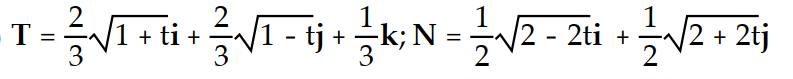
C)
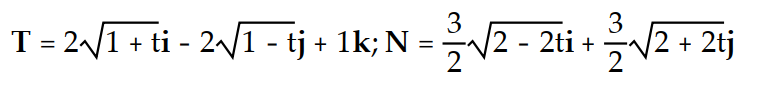
D)
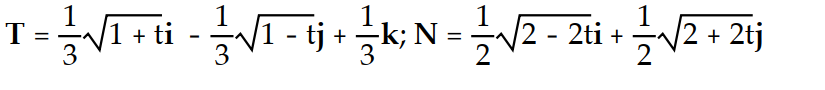

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
74
FInd the tangential and normal components of the acceleration.
-r(t) =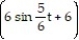 i +
i + 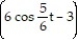 j + 12tk
j + 12tk
A) a =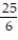 N
N
B) a = 25T + 25N
C) a = T + 25N
D) a =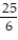 T
T
-r(t) =
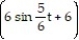 i +
i + 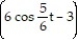 j + 12tk
j + 12tkA) a =
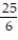 N
NB) a = 25T + 25N
C) a = T + 25N
D) a =
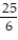 T
T
Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
75
FInd the tangential and normal components of the acceleration.
-r(t) = (t + 6)i + (ln(sec t) - 1)j + 7k, - /2 < t < /2
A) a = (sec t tan t)T + (sec t)N
B) a = (csc t)T + (sec t)N
C) a = (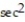 t)T + (cos t)N
t)T + (cos t)N
D) a = (cos t)T + (cos t)N
-r(t) = (t + 6)i + (ln(sec t) - 1)j + 7k, - /2 < t < /2
A) a = (sec t tan t)T + (sec t)N
B) a = (csc t)T + (sec t)N
C) a = (
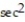 t)T + (cos t)N
t)T + (cos t)ND) a = (cos t)T + (cos t)N

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
76
FInd the tangential and normal components of the acceleration.
-r(t) = (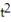 - 3)i + ( 2t - 4)j + 9k
- 3)i + ( 2t - 4)j + 9k
A)
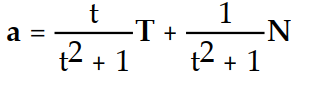
B)
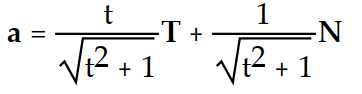
C)
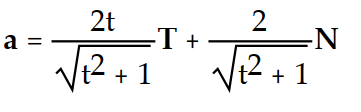
D)
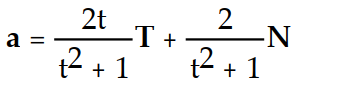
-r(t) = (
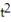 - 3)i + ( 2t - 4)j + 9k
- 3)i + ( 2t - 4)j + 9kA)
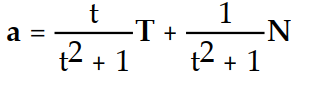
B)
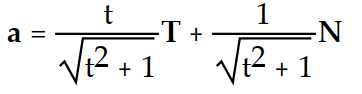
C)
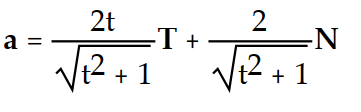
D)
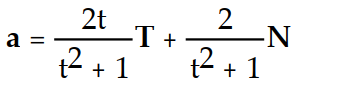

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
77
FInd the tangential and normal components of the acceleration.
-r(t) = ( 8t sin t + 8 cos t)i + ( 8t cos t - 8 sin t)j + 8k
A) a =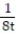 N
N
B) a = 8T + 8tN
C) a = 8T +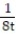 N
N
D) a = 8tN
-r(t) = ( 8t sin t + 8 cos t)i + ( 8t cos t - 8 sin t)j + 8k
A) a =
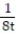 N
NB) a = 8T + 8tN
C) a = 8T +
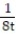 N
ND) a = 8tN

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
78
FInd the tangential and normal components of the acceleration.
-r(t) = (cosh t)i + (sinh t)j + tk
A) a = (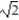 sinh t)T + N
sinh t)T + N
B) a = (-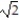 sinh t)T + N
sinh t)T + N
C) a = (sinh t)T + N
D) a = (-sinh t)T + N
-r(t) = (cosh t)i + (sinh t)j + tk
A) a = (
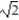 sinh t)T + N
sinh t)T + NB) a = (-
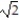 sinh t)T + N
sinh t)T + NC) a = (sinh t)T + N
D) a = (-sinh t)T + N

Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
79
FInd the tangential and normal components of the acceleration.
-r(t) = 4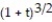 i + 4
i + 4 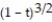 j + 3tk
j + 3tk
A) a = T + 3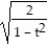 N
N
B) a = 3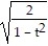 N
N
C) a =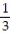
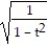 N
N
D) a = 3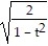 T
T
-r(t) = 4
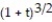 i + 4
i + 4 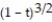 j + 3tk
j + 3tkA) a = T + 3
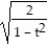 N
NB) a = 3
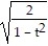 N
NC) a =
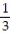
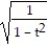 N
ND) a = 3
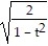 T
T
Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck
80
Compute the unit binormal vector and torsion of the curve.
-r(t) =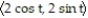
A) B(t) =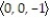 ,
, 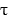 = 0
= 0
B) B(t) =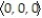 , 11ee983d_146e_64f2_a6de_f3be5c6bdb70_TB9662_11 = 0
, 11ee983d_146e_64f2_a6de_f3be5c6bdb70_TB9662_11 = 0
C) B(t) =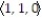 , 11ee983d_146e_64f2_a6de_f3be5c6bdb70_TB9662_11 = 1
, 11ee983d_146e_64f2_a6de_f3be5c6bdb70_TB9662_11 = 1
D) B(t) =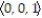 ,11ee983d_146e_64f2_a6de_f3be5c6bdb70_TB9662_11= 1
,11ee983d_146e_64f2_a6de_f3be5c6bdb70_TB9662_11= 1
-r(t) =
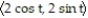
A) B(t) =
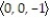 ,
, 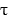 = 0
= 0B) B(t) =
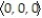 , 11ee983d_146e_64f2_a6de_f3be5c6bdb70_TB9662_11 = 0
, 11ee983d_146e_64f2_a6de_f3be5c6bdb70_TB9662_11 = 0C) B(t) =
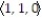 , 11ee983d_146e_64f2_a6de_f3be5c6bdb70_TB9662_11 = 1
, 11ee983d_146e_64f2_a6de_f3be5c6bdb70_TB9662_11 = 1D) B(t) =
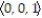 ,11ee983d_146e_64f2_a6de_f3be5c6bdb70_TB9662_11= 1
,11ee983d_146e_64f2_a6de_f3be5c6bdb70_TB9662_11= 1
Unlock Deck
Unlock for access to all 83 flashcards in this deck.
Unlock Deck
k this deck


