Exam 14: Vector-Valued Functions
Exam 1: Functions226 Questions
Exam 2: Limits224 Questions
Exam 3: Derivatives367 Questions
Exam 4: Applications of the Derivative228 Questions
Exam 5: Integration166 Questions
Exam 6: Applications of Integration211 Questions
Exam 7: Logarithmic, Exponential, and Hyperbolic Functions85 Questions
Exam 8: Integration Techniques287 Questions
Exam 9: Differential Equations76 Questions
Exam 10: Sequences and Infinite Series173 Questions
Exam 11: Power Series103 Questions
Exam 12: Parametric and Polar Curves169 Questions
Exam 13: Vectors and the Geometry of Space131 Questions
Exam 14: Vector-Valued Functions83 Questions
Exam 15: Functions of Several Variables229 Questions
Exam 16: Multiple Integration299 Questions
Exam 17: Vector Calculus173 Questions
Select questions type
Find the unit tangent vector T and the principal unit normal vector N.
-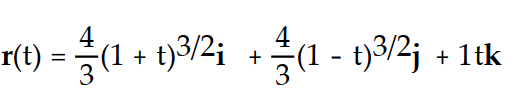
Free
(Multiple Choice)
4.9/5  (36)
(36)
Correct Answer:
A
The position vector of a particle is r(t). Find the requested vector.
-The acceleration at t = 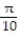 for r(t) = ( 9 sin 5t)i - ( 10 cos 5t)j + ( 2 csc 5t)k
for r(t) = ( 9 sin 5t)i - ( 10 cos 5t)j + ( 2 csc 5t)k
Free
(Multiple Choice)
4.9/5  (29)
(29)
Correct Answer:
C
Find the unit tangent vector T and the principal unit normal vector N.
-r(t) = (ln(cos t) + 9)i + 9j + ( 10 + t )k, - /2 < t < /2
Free
(Multiple Choice)
4.8/5  (27)
(27)
Correct Answer:
D
Compute the unit binormal vector and torsion of the curve.
-r(t) = 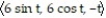
(Multiple Choice)
4.9/5  (38)
(38)
Graph the curve described by the function. Use analysis to anticipate the shape of the curve before using a graphing utility.
-r(t) = 3 cos t i + 2 sin t j + cos 5t k, for 0 t 2
(Multiple Choice)
4.8/5  (42)
(42)
The position vector of a particle is r(t). Find the requested vector.
-The acceleration at t = 2 for r(t) = ( 7t - 3 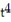 )i + ( 10 - t)j + ( 2
)i + ( 10 - t)j + ( 2 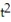 - 3t)k
- 3t)k
(Multiple Choice)
4.7/5  (43)
(43)
FInd the tangential and normal components of the acceleration.
-r(t) = (t + 6)i + (ln(sec t) - 1)j + 7k, - /2 < t < /2
(Multiple Choice)
4.7/5  (48)
(48)
Find the unit tangent vector T and the principal unit normal vector N.
-r(t) = ( 7t sin t + 7cos t)i + ( 7t cos t - 7 sin t)j - 4k
(Multiple Choice)
4.8/5  (43)
(43)
Compute the unit binormal vector and torsion of the curve.
-r(t) = 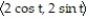
(Multiple Choice)
4.8/5  (35)
(35)
The position vector of a particle is r(t). Find the requested vector.
-The velocity at t = 3 for r(t) = ( 8 - 4 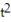 )i + ( 6t + 7)j -
)i + ( 6t + 7)j - 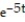 k
k
(Multiple Choice)
4.7/5  (38)
(38)
Find a function r(t) that describes the curve where the surfaces intersect.
-z = 16; z = 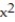 +
+ 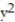
(Multiple Choice)
4.8/5  (45)
(45)
Find the length of the indicated portion of the trajectory.
-r(t) = ( 2cos t)i + ( 2sin t)j + 5tk, 0 t /2
(Multiple Choice)
4.8/5  (41)
(41)
Find the curvature of the curve r(t).
-r(t) = ( 8 + ln(sec t))i + ( 3 + t)k, - /2 < t < /2
(Multiple Choice)
4.8/5  (41)
(41)
Verify that the curve r(t) lies on the surface. Give the name of the surface.
-r(t) = 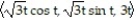 ; z=
; z= 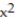 +
+ 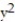
(Multiple Choice)
4.8/5  (35)
(35)
Find the length of the indicated portion of the trajectory.
-r(t) = (1 + 5t)i + (1 + 8t)j + ( 2 - 2t)k, -1 t 0
(Multiple Choice)
4.8/5  (37)
(37)
Find the length of the indicated portion of the trajectory.
-r(t) = ( 2 + 2t)i + ( 3 + 3t)j + ( 3 - 6t)k, -1 t 0
(Multiple Choice)
4.9/5  (39)
(39)
Find the curvature of the space curve.
-r(t) = ( 9 t sin t + 9 cos t)i + 9j + ( 9t cos t - 9 sin t)k
(Multiple Choice)
4.9/5  (30)
(30)
Find the unit tangent vector of the given curve.
-r(t) = ( 6 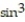 2t)i + ( 6
2t)i + ( 6 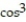 2t)j
2t)j
(Multiple Choice)
5.0/5  (42)
(42)
Showing 1 - 20 of 83
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)