Deck 11: Power Series
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/103
Play
Full screen (f)
Deck 11: Power Series
1
Find the linear approximating polynomial for the function centered at a.
-f(x) = 2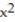 + 3x - 5, a = -2
+ 3x - 5, a = -2
A) L(x) = -5x - 13
B) L(x) = -11x -13
C) L(x) = -11x + 3
D) L(x) = -5x + 3
-f(x) = 2
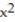 + 3x - 5, a = -2
+ 3x - 5, a = -2A) L(x) = -5x - 13
B) L(x) = -11x -13
C) L(x) = -11x + 3
D) L(x) = -5x + 3
L(x) = -5x - 13
2
Find the linear approximating polynomial for the function centered at a.
-f(x) =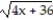 , a = 0
, a = 0
A) L(x) =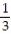 x - 6
x - 6
B) L(x) =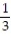 x + 6
x + 6
C) L(x) =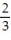 x - 6
x - 6
D) L(x) =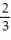 x + 6
x + 6
-f(x) =
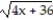 , a = 0
, a = 0A) L(x) =
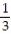 x - 6
x - 6B) L(x) =
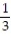 x + 6
x + 6C) L(x) =
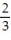 x - 6
x - 6D) L(x) =
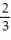 x + 6
x + 6L(x) = 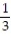 x + 6
x + 6
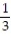 x + 6
x + 6 3
Find the linear approximating polynomial for the function centered at a.
-f(x) =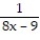 , a = 0
, a = 0
A) L(x) =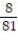 x +
x + 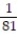
B) L(x) = -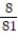 x +
x + 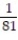
C)L(x) =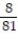 x -
x - 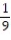
D) L(x) = -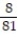 x -
x - 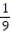
-f(x) =
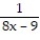 , a = 0
, a = 0A) L(x) =
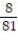 x +
x + 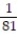
B) L(x) = -
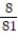 x +
x + 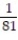
C)L(x) =
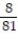 x -
x - 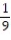
D) L(x) = -
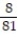 x -
x - 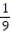
L(x) = - 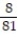 x -
x - 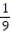
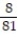 x -
x - 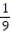
4
Find the linear approximating polynomial for the function centered at a.
-f(x) =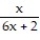 , a = 0
, a = 0
A)L(x) =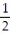 x
x
B) L(x) = x
x
C) L(x) = -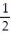 x
x
D) L(x) = - x
x
-f(x) =
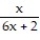 , a = 0
, a = 0A)L(x) =
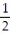 x
xB) L(x) =
 x
xC) L(x) = -
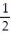 x
xD) L(x) = -
 x
x
Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
5
Find the linear approximating polynomial for the function centered at a.
-f(x) = x + , a = 4
, a = 4
A) L(x) =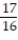 x +
x + 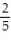
B) L(x) =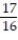 x +
x + 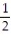
C) L(x) =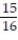 x +
x + 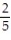
D) L(x) =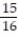 x +
x + 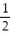
-f(x) = x +
 , a = 4
, a = 4A) L(x) =
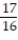 x +
x + 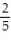
B) L(x) =
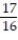 x +
x + 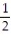
C) L(x) =
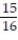 x +
x + 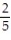
D) L(x) =
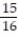 x +
x + 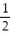

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
6
Find the linear approximating polynomial for the function centered at a.
-f(x) =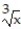 , a = 8
, a = 8
A) L(x) =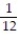 x +
x + 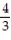
B) L(x) = x +
x + 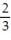
C) L(x) =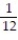 x +
x + 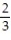
D) L(x) = x + 4
x + 4
-f(x) =
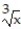 , a = 8
, a = 8A) L(x) =
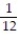 x +
x + 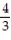
B) L(x) =
 x +
x + 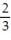
C) L(x) =
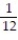 x +
x + 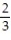
D) L(x) =
 x + 4
x + 4
Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
7
Find the linear approximating polynomial for the function centered at a.
-f(x) = tan x, a =
A) L(x) = x -2
B) L(x) = x +
C) L(x) = x -
D) L(x) = 2x -
-f(x) = tan x, a =
A) L(x) = x -2
B) L(x) = x +
C) L(x) = x -
D) L(x) = 2x -

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
8
Find the linear approximating polynomial for the function centered at a.
-f(x) = tan x, a = 0
A) L(x) = 0
B) L(x) = 5x + 1
C) L(x) = x
D) L(x) = -x
-f(x) = tan x, a = 0
A) L(x) = 0
B) L(x) = 5x + 1
C) L(x) = x
D) L(x) = -x

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
9
Find the quadratic approximation of f at x = 0.
-f(x) =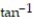 2x
2x
A) Q(x) = 1 - 2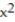
B) Q(x) = 2x
C) Q(x) = 1 + 2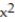
D) Q(x) 1 + 1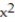
-f(x) =
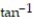 2x
2xA) Q(x) = 1 - 2
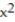
B) Q(x) = 2x
C) Q(x) = 1 + 2
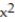
D) Q(x) 1 + 1
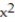

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
10
Find the quadratic approximation of f at x = 0.
-f(x) = tan 7x
A) Q(x) = 1 -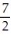
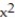
B) Q(x) = 7x
C) Q(x) = 1 +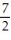
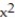
D) Q(x) = 1 + 7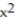
-f(x) = tan 7x
A) Q(x) = 1 -
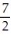
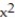
B) Q(x) = 7x
C) Q(x) = 1 +
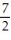
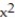
D) Q(x) = 1 + 7
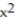

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
11
Find the quadratic approximation of f at x = 0.
-f(x) =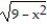
A) Q(x) = 3 -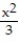
B) Q(x) = 3 -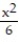
C) Q(x) = 3 +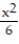
D) Q(x) = 3 +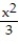
-f(x) =
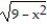
A) Q(x) = 3 -
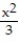
B) Q(x) = 3 -
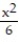
C) Q(x) = 3 +
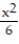
D) Q(x) = 3 +
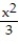

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
12
Find the quadratic approximation of f at x = 0.
-f(x) = ln(cos 2x)
A) Q(x) = 2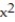
B) Q(x) = -2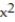
C) Q(x) = 1 + 2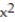
D) Q(x) = 1 - 2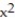
-f(x) = ln(cos 2x)
A) Q(x) = 2
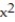
B) Q(x) = -2
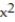
C) Q(x) = 1 + 2
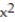
D) Q(x) = 1 - 2
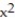

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
13
Find the quadratic approximation of f at x = 0.
-f(x) = ln(1 + sin 10x)
A) Q(x) = 1 - 10x + 50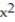
B) Q(x) = 10x + 50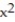
C) Q(x) = 10x - 50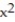
D) Q(x) = 1 + 10x + 50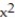
-f(x) = ln(1 + sin 10x)
A) Q(x) = 1 - 10x + 50
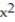
B) Q(x) = 10x + 50
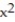
C) Q(x) = 10x - 50
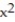
D) Q(x) = 1 + 10x + 50
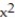

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
14
Find the quadratic approximation of f at x = 0.
-f(x) =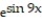
A) Q(x) = 1 + 9x +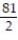
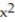
B) Q(x) = 9x -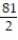
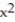
C) Q(x) = 1 - 9x +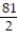
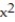
D) Q(x) = 9x +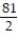
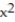
-f(x) =
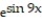
A) Q(x) = 1 + 9x +
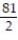
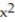
B) Q(x) = 9x -
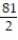
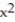
C) Q(x) = 1 - 9x +
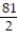
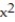
D) Q(x) = 9x +
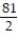
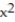

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
15
Find the quadratic approximation of f at x = 0.
-f(x) =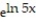
A) Q(x) = 5x +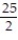
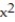
B) Q(x) = 1 + 5x +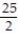
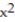
C) Q(x) = 5x
D) Q(x) = 5x -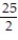
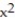
-f(x) =
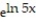
A) Q(x) = 5x +
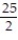
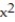
B) Q(x) = 1 + 5x +
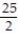
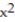
C) Q(x) = 5x
D) Q(x) = 5x -
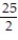
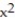

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
16
Find the quadratic approximation of f at x = 0.
-f(x) = x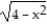
A) Q(x) = 4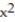
B) Q(x) = 1 - 2x
C) Q(x) = 2x
D) Q(x) = 1 + 2x
-f(x) = x
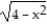
A) Q(x) = 4
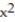
B) Q(x) = 1 - 2x
C) Q(x) = 2x
D) Q(x) = 1 + 2x

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
17
Find the quadratic approximation of f at x = 0.
-f(x) =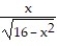
A) Q(x) = 4x
B) Q(x) = 1 +
C) Q(x) =
D)Q(x) = 1 + 4x
-f(x) =
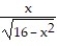
A) Q(x) = 4x
B) Q(x) = 1 +

C) Q(x) =

D)Q(x) = 1 + 4x

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
18
Find the quadratic approximation of f at x = 0.
-f(x) = sin ln( 2x + 1)
A) Q(x) = 1 + 2x + 2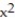
B) Q(x) = 2x - 2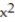
C) Q(x) = 2x + 2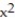
D) Q(x) = 1 - 2x + 2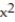
-f(x) = sin ln( 2x + 1)
A) Q(x) = 1 + 2x + 2
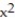
B) Q(x) = 2x - 2
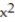
C) Q(x) = 2x + 2
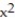
D) Q(x) = 1 - 2x + 2
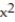

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
19
Find the Taylor polynomial of order 3 centered at 0.
-f(x) =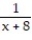
A)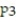 (x) =
(x) = 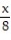 +
+ 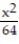 +
+ 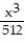 +
+ 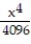
B)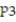 (x) =
(x) = 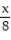 -
- 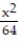 +
+ 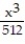 -
- 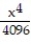
C)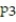 (x) =
(x) = 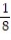 -
- 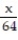 +
+ 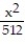 -
- 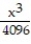
D)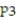 (x) =
(x) = 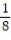 +
+ 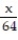 +
+ 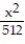 +
+ 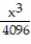
-f(x) =
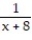
A)
 (x) =
(x) = 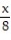 +
+ 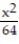 +
+ 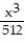 +
+ 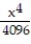
B)
 (x) =
(x) = 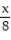 -
- 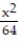 +
+ 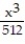 -
- 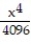
C)
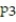 (x) =
(x) = 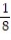 -
- 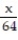 +
+ 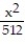 -
- 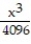
D)
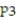 (x) =
(x) = 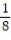 +
+ 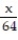 +
+ 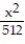 +
+ 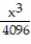

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
20
Find the Taylor polynomial of order 3 centered at 0.
-f(x) =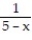
A)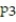 (x) =
(x) = 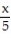 -
- 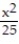 +
+ 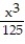 -
- 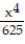
B)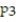 (x) =
(x) = 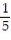 +
+ 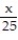 +
+ 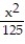 +
+ 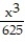
C)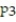 (x) =
(x) = 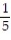 -
- 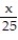 +
+ 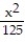 -
- 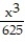
D)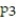 (x) =
(x) = 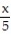 +
+ 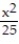 +
+ 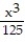 +
+ 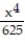
-f(x) =
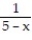
A)
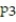 (x) =
(x) = 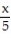 -
- 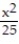 +
+ 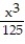 -
- 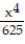
B)
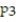 (x) =
(x) = 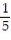 +
+ 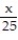 +
+ 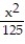 +
+ 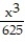
C)
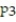 (x) =
(x) = 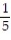 -
- 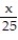 +
+ 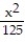 -
- 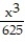
D)
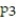 (x) =
(x) = 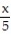 +
+ 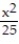 +
+ 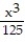 +
+ 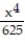

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
21
Find the Taylor polynomial of order 3 centered at 0.
-f(x) =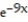
A)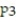 (x) = 1 - 9x +
(x) = 1 - 9x + 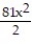 -
- 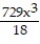
B)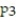 (x) = 1 - 81x +
(x) = 1 - 81x + 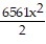 -
- 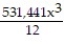
C)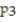 (x) = 1 - 9x +
(x) = 1 - 9x + 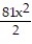 -
- 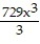
D)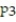 (x) = 1 - 9x +
(x) = 1 - 9x + 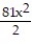 -
- 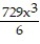
-f(x) =
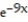
A)
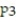 (x) = 1 - 9x +
(x) = 1 - 9x + 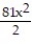 -
- 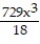
B)
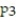 (x) = 1 - 81x +
(x) = 1 - 81x + 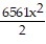 -
- 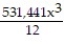
C)
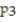 (x) = 1 - 9x +
(x) = 1 - 9x + 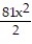 -
- 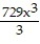
D)
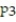 (x) = 1 - 9x +
(x) = 1 - 9x + 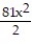 -
- 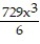

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
22
Find the Taylor polynomial of order 3 generated by f at a.
-f(x) =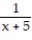 , a = 1
, a = 1
A)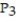 (x) =
(x) =  -
- 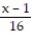 +
+ 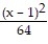 -
- 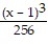
B) (x) =
(x) =  -
- 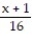 +
+ 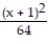 -
- 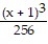
C) (x) =
(x) = 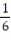 -
- 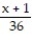 +
+ 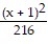 -
- 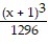
D)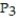 (x) =
(x) = 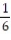 -
- 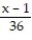 +
+ 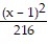 -
- 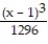
-f(x) =
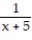 , a = 1
, a = 1A)
 (x) =
(x) =  -
- 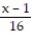 +
+ 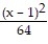 -
- 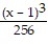
B)
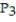 (x) =
(x) =  -
-  +
+ 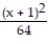 -
- 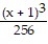
C)
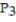 (x) =
(x) = 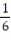 -
- 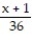 +
+ 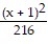 -
- 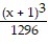
D)
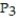 (x) =
(x) = 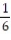 -
- 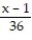 +
+ 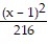 -
- 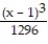

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
23
Find the Taylor polynomial of order 3 generated by f at a.
-f(x) =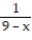 , a = 1
, a = 1
A)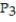 (x) =
(x) = 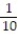 -
- 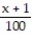 +
+ 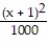 -
- 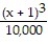
B)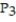 (x) =
(x) = 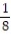 -
- 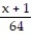 +
+ 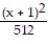 -
- 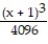
C) (x) =
(x) = 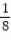 -
- 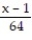 +
+ 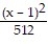 -
- 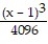
D)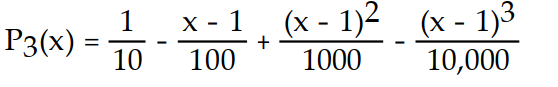
-f(x) =
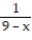 , a = 1
, a = 1A)
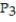 (x) =
(x) = 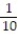 -
- 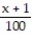 +
+ 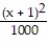 -
- 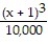
B)
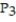 (x) =
(x) = 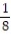 -
- 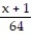 +
+ 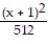 -
- 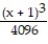
C)
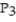 (x) =
(x) = 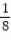 -
- 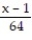 +
+ 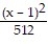 -
- 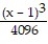
D)
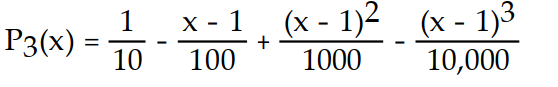

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
24
Find the Taylor polynomial of order 3 generated by f at a.
-f(x) = ln x, a = 3
A)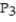 (x) =
(x) = 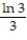 -
- 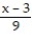 +
+ 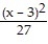 -
- 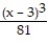
B) (x) =
(x) = 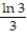 +
+ 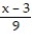 +
+ 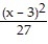 +
+ 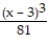
C)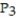 (x) = ln 3 -
(x) = ln 3 - 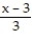 +
+ 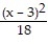 -
- 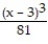
D)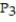 (x) = ln 3 +
(x) = ln 3 + 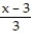 -
- 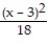 +
+ 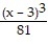
-f(x) = ln x, a = 3
A)
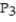 (x) =
(x) = 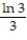 -
- 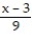 +
+ 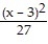 -
- 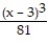
B)
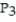 (x) =
(x) = 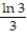 +
+ 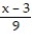 +
+ 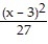 +
+ 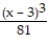
C)
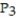 (x) = ln 3 -
(x) = ln 3 - 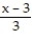 +
+ 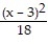 -
- 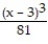
D)
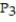 (x) = ln 3 +
(x) = ln 3 + 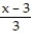 -
- 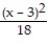 +
+ 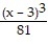

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
25
Find the Taylor polynomial of order 3 generated by f at a.
-f(x) = ln(x + 1), a = 5
A)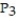 (x) = ln 6 -
(x) = ln 6 - 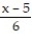 +
+ 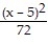 -
- 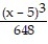
B)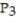 (x) = ln 4 -
(x) = ln 4 - 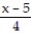 +
+ 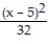 -
- 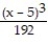
C)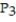 (x) = ln 4 +
(x) = ln 4 + 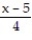 +
+ 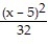 +
+ 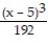
D)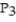 (x) = ln 6 +
(x) = ln 6 + 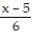 -
- 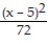 +
+ 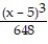
-f(x) = ln(x + 1), a = 5
A)
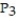 (x) = ln 6 -
(x) = ln 6 - 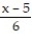 +
+ 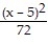 -
- 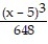
B)
 (x) = ln 4 -
(x) = ln 4 - 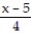 +
+ 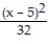 -
- 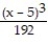
C)
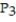 (x) = ln 4 +
(x) = ln 4 + 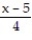 +
+ 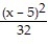 +
+ 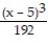
D)
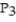 (x) = ln 6 +
(x) = ln 6 + 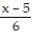 -
- 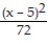 +
+ 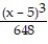

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
26
Find the Taylor polynomial of order 3 generated by f at a.
-f(x) =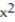 , a = 3
, a = 3
A)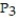 (x) = 1 + 18(x - 3) + 81
(x) = 1 + 18(x - 3) + 81 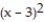 + 324
+ 324 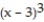
B) (x) = 1 + 6(x - 3) + 9
(x) = 1 + 6(x - 3) + 9 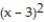 + 12
+ 12 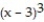
C)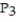 (x) = 9 + 6(x - 3) +
(x) = 9 + 6(x - 3) + 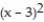
D)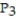 (x) = 9 + 6(x - 3) + 9
(x) = 9 + 6(x - 3) + 9 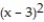 + 12
+ 12 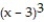
-f(x) =
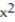 , a = 3
, a = 3A)
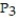 (x) = 1 + 18(x - 3) + 81
(x) = 1 + 18(x - 3) + 81 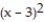 + 324
+ 324 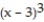
B)
 (x) = 1 + 6(x - 3) + 9
(x) = 1 + 6(x - 3) + 9 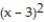 + 12
+ 12 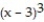
C)
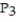 (x) = 9 + 6(x - 3) +
(x) = 9 + 6(x - 3) + 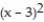
D)
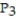 (x) = 9 + 6(x - 3) + 9
(x) = 9 + 6(x - 3) + 9 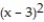 + 12
+ 12 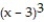

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
27
Find the Taylor polynomial of order 3 generated by f at a.
-f(x) =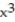 , a = 7
, a = 7
A)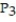 (x) = 6 + 3(x - 7) +
(x) = 6 + 3(x - 7) + 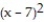 +
+ 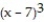
B)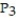 (x) = 1372 + 147(x - 7) + 14
(x) = 1372 + 147(x - 7) + 14 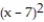 +
+ 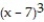
C)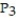 (x) = 343 + 147(x - 7) + 21
(x) = 343 + 147(x - 7) + 21 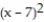 +
+ 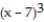
D)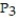 (x) = 343 + 49(x - 7) + 49
(x) = 343 + 49(x - 7) + 49 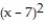 +
+ 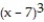
-f(x) =
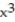 , a = 7
, a = 7A)
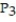 (x) = 6 + 3(x - 7) +
(x) = 6 + 3(x - 7) + 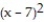 +
+ 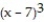
B)
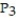 (x) = 1372 + 147(x - 7) + 14
(x) = 1372 + 147(x - 7) + 14 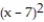 +
+ 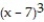
C)
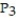 (x) = 343 + 147(x - 7) + 21
(x) = 343 + 147(x - 7) + 21 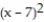 +
+ 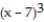
D)
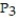 (x) = 343 + 49(x - 7) + 49
(x) = 343 + 49(x - 7) + 49 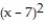 +
+ 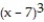

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
28
Find the Taylor polynomial of order 3 generated by f at a.
-f(x) =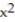 + x + 1, a = 4
+ x + 1, a = 4
A)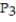 (x) = 5 + 9(x - 4) + 13
(x) = 5 + 9(x - 4) + 13 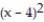
B)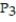 (x) = 1 + 3(x - 4) + 3
(x) = 1 + 3(x - 4) + 3 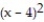 +
+ 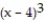
C)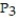 (x) = 21 + 9(x - 4) +
(x) = 21 + 9(x - 4) + 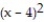
D)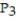 (x) = 21 + 9(x - 4) + 9
(x) = 21 + 9(x - 4) + 9 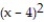 + 21
+ 21 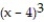
-f(x) =
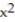 + x + 1, a = 4
+ x + 1, a = 4A)
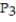 (x) = 5 + 9(x - 4) + 13
(x) = 5 + 9(x - 4) + 13 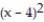
B)
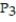 (x) = 1 + 3(x - 4) + 3
(x) = 1 + 3(x - 4) + 3 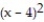 +
+ 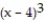
C)
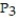 (x) = 21 + 9(x - 4) +
(x) = 21 + 9(x - 4) + 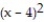
D)
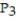 (x) = 21 + 9(x - 4) + 9
(x) = 21 + 9(x - 4) + 9 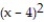 + 21
+ 21 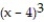

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
29
Find the series' radius of convergence.
-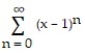
A) , for all x
B) 2
C) 1
D) 0
-
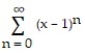
A) , for all x
B) 2
C) 1
D) 0

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
30
Find the series' radius of convergence.
-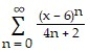
A) 0
B) 1
C) , for all x
D) 2
-
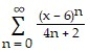
A) 0
B) 1
C) , for all x
D) 2

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
31
Find the series' radius of convergence.
-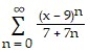
A) 2
B) , for all x
C) 0
D) 1
-
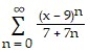
A) 2
B) , for all x
C) 0
D) 1

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
32
Find the series' radius of convergence.
-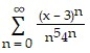
A) 8
B) 4
C) 0
D) , for all x
-
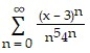
A) 8
B) 4
C) 0
D) , for all x

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
33
Find the series' radius of convergence.
-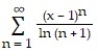
A) 0
B) , for all x
C) 2
D) 1
-
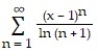
A) 0
B) , for all x
C) 2
D) 1

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
34
Find the series' radius of convergence.
-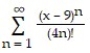
A) 2
B) 0
C) , for all x
D) 1
-
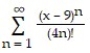
A) 2
B) 0
C) , for all x
D) 1

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
35
Find the series' radius of convergence.
-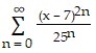
A) 1
B) , for all x
C) 5
D) 10
-
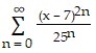
A) 1
B) , for all x
C) 5
D) 10

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
36
Find the series' radius of convergence.
-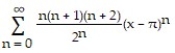
A) , for all x
B) 4
C) 2
D) 1
-
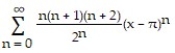
A) , for all x
B) 4
C) 2
D) 1

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
37
Find the series' radius of convergence.
-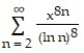
A) , for all x
B) 2
C) 1
D) 0
-
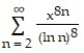
A) , for all x
B) 2
C) 1
D) 0

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
38
Determine the radius of convergence of the power series.
-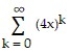
A)
B) 1
C)
D) 4
-
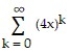
A)
B) 1
C)

D) 4

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
39
Determine the radius of convergence of the power series.
-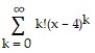
A) 4
B) 0
C) 8
D)
-
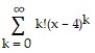
A) 4
B) 0
C) 8
D)

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
40
Find the interval of convergence of the series.
-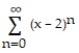
A) -3 < x < 3
B) 1 x < 3
C) 1 < x < 3
D) x < 3
-
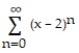
A) -3 < x < 3
B) 1 x < 3
C) 1 < x < 3
D) x < 3

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
41
Find the interval of convergence of the series.
-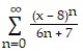
A) x < 9
B) 7 x < 9
C) 2 x < 14
D) 7 < x < 9
-
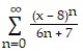
A) x < 9
B) 7 x < 9
C) 2 x < 14
D) 7 < x < 9

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
42
Find the interval of convergence of the series.
-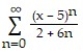
A) 1 < x < 9
B) -1 x 11
C) 4 x < 6
D) -1 < x < 11
-
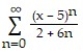
A) 1 < x < 9
B) -1 x 11
C) 4 x < 6
D) -1 < x < 11

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
43
Find the interval of convergence of the series.
-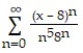
A) -16 < x < 16
B) 7 x 9
C) x < 16
D) 0 x 16
-
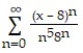
A) -16 < x < 16
B) 7 x 9
C) x < 16
D) 0 x 16

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
44
Find the interval of convergence of the series.
-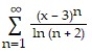
A) 2 x < 4
B) - < x <
C) 2 < x < 4
D) x < 4
-
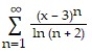
A) 2 x < 4
B) - < x <
C) 2 < x < 4
D) x < 4

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
45
Find the interval of convergence of the series.
-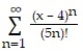
A) x 5
B) 3 x 5
C) - < x <
D) -116 x 124
-
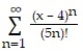
A) x 5
B) 3 x 5
C) - < x <
D) -116 x 124

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
46
Find the interval of convergence of the series.
-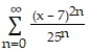
A) x < 12
B) 6 < x < 8
C)-12 < x < 12
D) 2 < x < 12
-
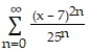
A) x < 12
B) 6 < x < 8
C)-12 < x < 12
D) 2 < x < 12

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
47
Determine the interval of convergence of the power series.
-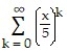
A) (-6, 4)
B)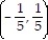
C) (- , )
D) (-5, 5)
-
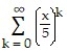
A) (-6, 4)
B)
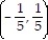
C) (- , )
D) (-5, 5)

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
48
Determine the interval of convergence of the power series.
-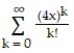
A)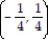
B) (-4, 4)
C) (- , )
D) x = 0
-
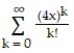
A)
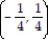
B) (-4, 4)
C) (- , )
D) x = 0

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
49
Find the function represented by the power series.
-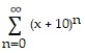
A)
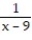
B)
-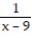
C)
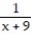
D)
-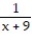
-
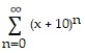
A)
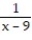
B)
-
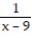
C)
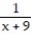
D)
-
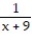

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
50
Find the function represented by the power series.
-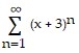
A)
-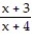
B)
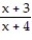
C)
-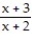
D)
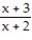
-
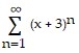
A)
-
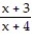
B)
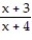
C)
-
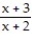
D)
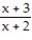

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
51
Find the function represented by the power series.
-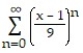
A)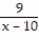
B) -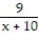
C)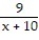
D) -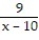
-
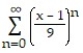
A)
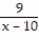
B) -
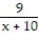
C)
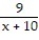
D) -
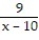

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
52
Find the function represented by the power series.
-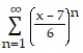
A) -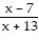
B) -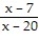
C) -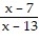
D)-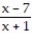
-
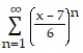
A) -
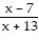
B) -
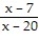
C) -
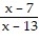
D)-
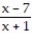

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
53
Find the function represented by the power series.
-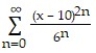
A)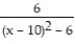
B) -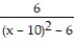
C)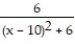
D)-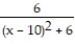
-
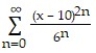
A)
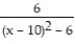
B) -
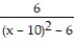
C)
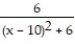
D)-
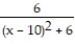

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
54
Find the function represented by the power series.
-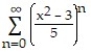
A) -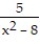
B)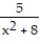
C)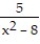
D) -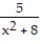
-
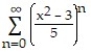
A) -
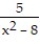
B)
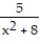
C)
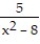
D) -

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
55
Find the first four nonzero terms in the Maclaurin series for the function.
-f(x) =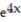
A) 1 + 4x +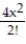 +
+ 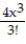 + . . .
+ . . .
B) 1 + 4x +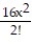 +
+ 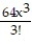 + . . .
+ . . .
C) x + 4x +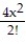 +
+ 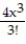 + . . .
+ . . .
D) 4x + 64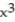 + 1024
+ 1024 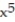 + 16,384
+ 16,384 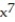 + . . .
+ . . .
-f(x) =
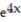
A) 1 + 4x +
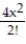 +
+ 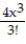 + . . .
+ . . .B) 1 + 4x +
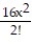 +
+ 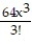 + . . .
+ . . .C) x + 4x +
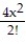 +
+ 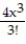 + . . .
+ . . .D) 4x + 64
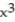 + 1024
+ 1024 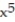 + 16,384
+ 16,384 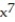 + . . .
+ . . .
Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
56
Find the first four nonzero terms in the Maclaurin series for the function.
-f(x) =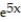
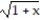
A)
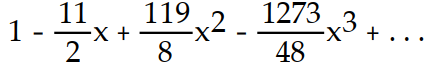
B)
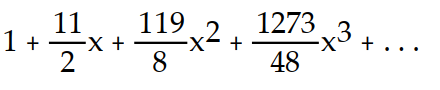
C)
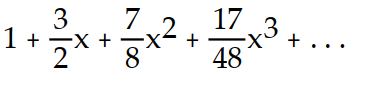
D)
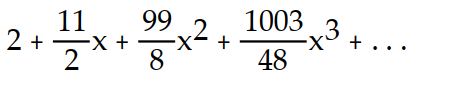
-f(x) =
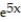
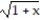
A)
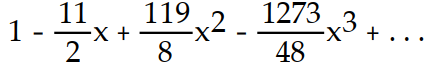
B)
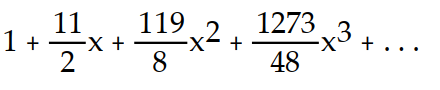
C)
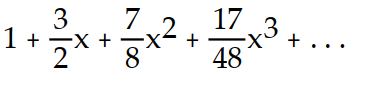
D)
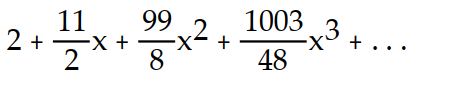

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
57
Find the first four nonzero terms in the Maclaurin series for the function.
-f(x) = ln (1 +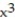 )
)
A)
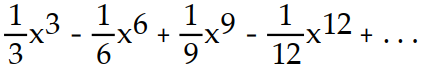
B)
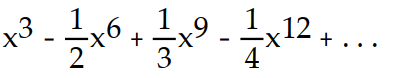
C)
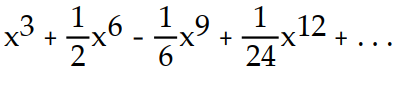
D)
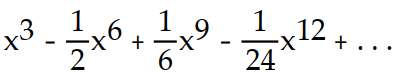
-f(x) = ln (1 +
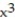 )
)A)
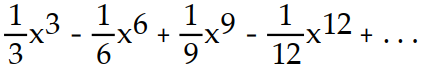
B)
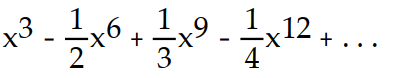
C)
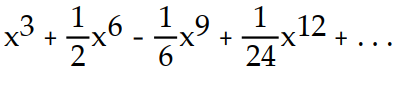
D)
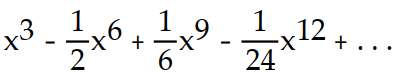

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
58
Find the first four nonzero terms in the Maclaurin series for the function.
-f(x) = x sin( 3x)
A)
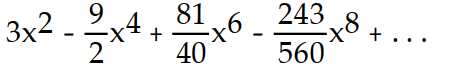
B)
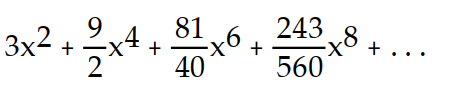
C)
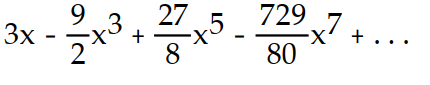
D)
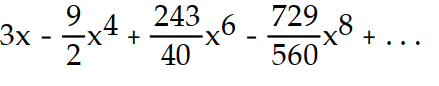
-f(x) = x sin( 3x)
A)
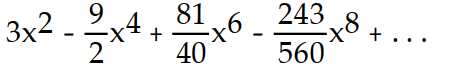
B)
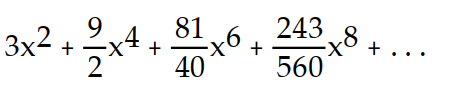
C)
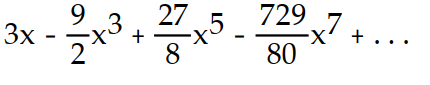
D)
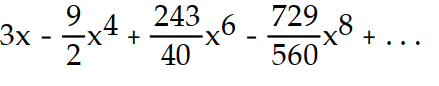

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
59
Find the first four nonzero terms in the Maclaurin series for the function.
-f(x) = sin x cos x
A)
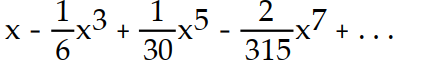
B)
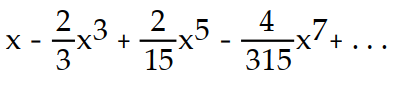
C)
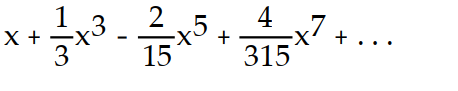
D)
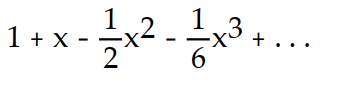
-f(x) = sin x cos x
A)
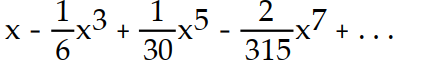
B)
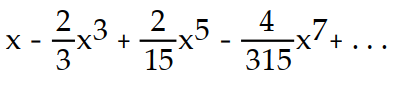
C)
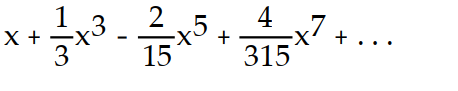
D)
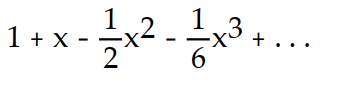

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
60
Find the Taylor series generated by f at x = a.
-f(x) = 8x + 2, a = 2
A) 8(x - 2) + 14
B) 8(x - 2) + 18
C) 8(x + 2) + 18
D) 8(x + 2) + 14
-f(x) = 8x + 2, a = 2
A) 8(x - 2) + 14
B) 8(x - 2) + 18
C) 8(x + 2) + 18
D) 8(x + 2) + 14

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
61
Find the Taylor series generated by f at x = a.
-f(x) =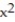 - 10x - 8, a = 3
- 10x - 8, a = 3
A)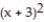 - 4(x + 3) - 13
- 4(x + 3) - 13
B)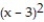 - 4(x - 3) - 29
- 4(x - 3) - 29
C)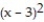 - 4(x - 3) - 13
- 4(x - 3) - 13
D)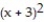 - 4(x + 3) - 29
- 4(x + 3) - 29
-f(x) =
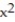 - 10x - 8, a = 3
- 10x - 8, a = 3A)
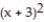 - 4(x + 3) - 13
- 4(x + 3) - 13B)
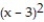 - 4(x - 3) - 29
- 4(x - 3) - 29C)
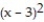 - 4(x - 3) - 13
- 4(x - 3) - 13D)
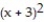 - 4(x + 3) - 29
- 4(x + 3) - 29
Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
62
Find the Taylor series generated by f at x = a.
-f(x) =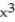 + 9
+ 9 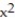 + 9x - 4, a = 5
+ 9x - 4, a = 5
A)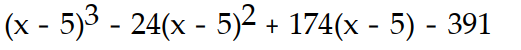
B)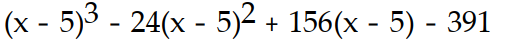
C)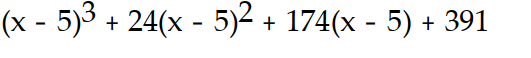
D)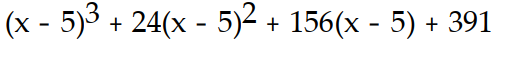
-f(x) =
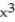 + 9
+ 9 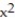 + 9x - 4, a = 5
+ 9x - 4, a = 5A)
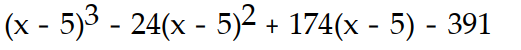
B)
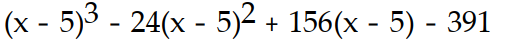
C)
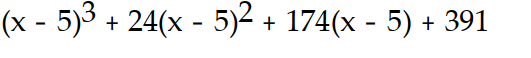
D)
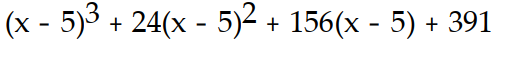

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
63
Find the Taylor series generated by f at x = a.
-f(x) =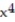 - 4
- 4 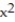 + 3x + 5, a = 5
+ 3x + 5, a = 5
A)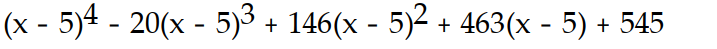
B)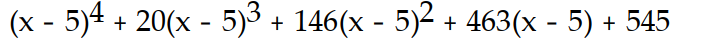
C)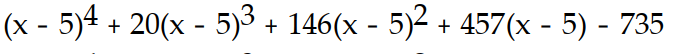
D)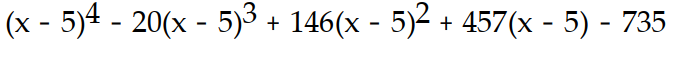
-f(x) =
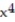 - 4
- 4 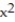 + 3x + 5, a = 5
+ 3x + 5, a = 5A)
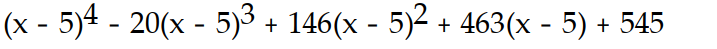
B)
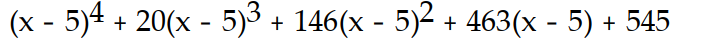
C)
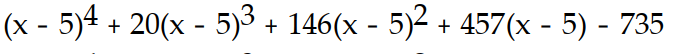
D)
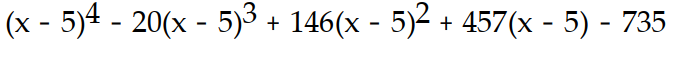

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
64
Find the Taylor series generated by f at x = a.
-f(x) = , a = 10
, a = 10
A)
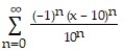
B)
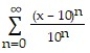
C)
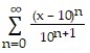
D)
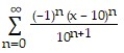
-f(x) =
 , a = 10
, a = 10A)
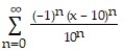
B)
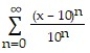
C)
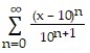
D)
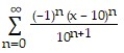

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
65
Find the Taylor series generated by f at x = a.
-f(x) =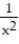 , a = 7
, a = 7
A)
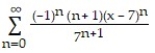
B)
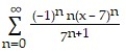
C)
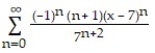
D)
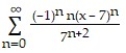
-f(x) =
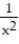 , a = 7
, a = 7A)
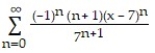
B)
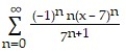
C)
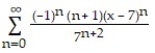
D)
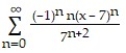

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
66
Find the Taylor series generated by f at x = a.
-f(x) =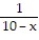 , a = 2
, a = 2
A)
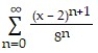
B)
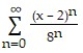
C)
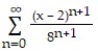
D)
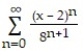
-f(x) =
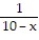 , a = 2
, a = 2A)
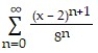
B)
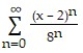
C)
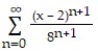
D)
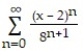

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
67
Find the Taylor series generated by f at x = a.
-f(x) =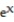 , a = 7
, a = 7
A)
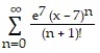
B)
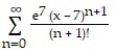
C)
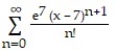
D)
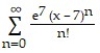
-f(x) =
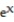 , a = 7
, a = 7A)
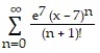
B)
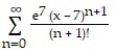
C)
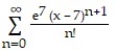
D)
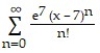

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
68
Find the Taylor series generated by f at x = a.
-f(x) =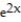 , a = 10
, a = 10
A)
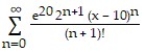
B)
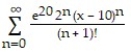
C)
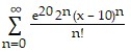
D)
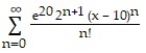
-f(x) =
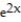 , a = 10
, a = 10A)
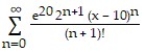
B)
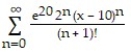
C)
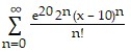
D)
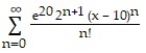

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
69
Find the Taylor series generated by f at x = a.
-f(x) =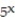 , a = 4
, a = 4
A)
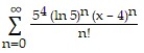
B)
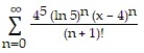
C)
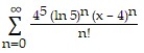
D)
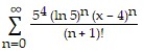
-f(x) =
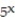 , a = 4
, a = 4A)
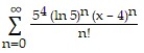
B)
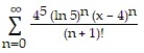
C)
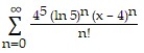
D)
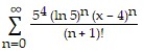

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
70
Use power series operations to find the Taylor series at x = 0 for the given function.
-f(x) =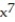
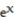
A)
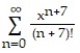
B)
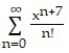
C)
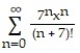
D)
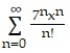
-f(x) =
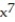
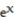
A)
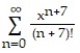
B)
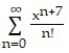
C)
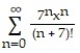
D)
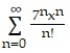

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
71
Use power series operations to find the Taylor series at x = 0 for the given function.
-f(x) =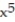
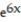
A)
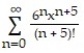
B)
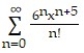
C)
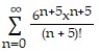
D)
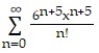
-f(x) =
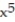
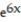
A)
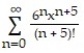
B)
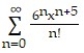
C)
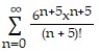
D)
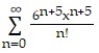

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
72
Use power series operations to find the Taylor series at x = 0 for the given function.
-f(x) =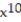 sin x
sin x
A)
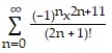
B)
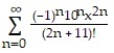
C)
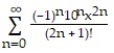
D)
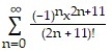
-f(x) =
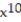 sin x
sin xA)
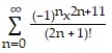
B)
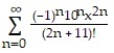
C)
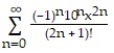
D)
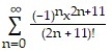

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
73
Use power series operations to find the Taylor series at x = 0 for the given function.
-f(x) =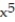 cos x
cos x
A)
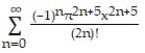
B)
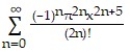
C)
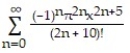
D)
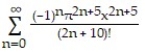
-f(x) =
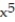 cos x
cos xA)
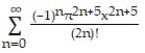
B)
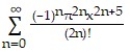
C)
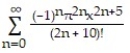
D)
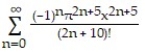

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
74
Use power series operations to find the Taylor series at x = 0 for the given function.
-f(x) =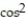 ( 4x)
( 4x)
A)
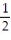 +
+ 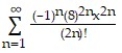
B)
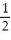 +
+ 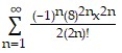
C)
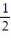 +
+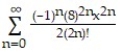
D)
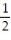 +
+ 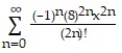
-f(x) =
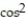 ( 4x)
( 4x)A)
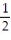 +
+ 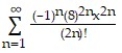
B)
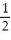 +
+ 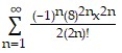
C)
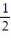 +
+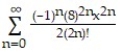
D)
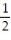 +
+ 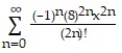

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
75
Use power series operations to find the Taylor series at x = 0 for the given function.
-f(x) =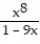
A)
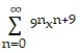
B)
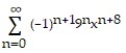
C)
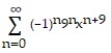
D)
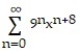
-f(x) =
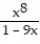
A)
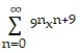
B)
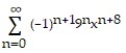
C)
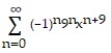
D)
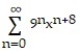

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
76
Use power series operations to find the Taylor series at x = 0 for the given function.
-f(x) =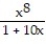
A)
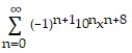
B)
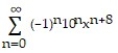
C)
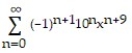
D)
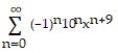
-f(x) =
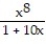
A)
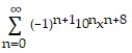
B)
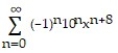
C)
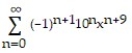
D)
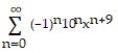

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
77
Use power series operations to find the Taylor series at x = 0 for the given function.
-f(x) =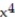 ln(1 + 4x)
ln(1 + 4x)
A)
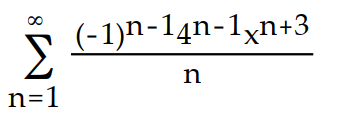
B)
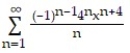
C)
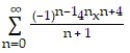
D)
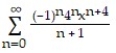
-f(x) =
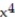 ln(1 + 4x)
ln(1 + 4x)A)
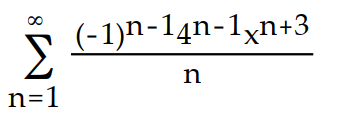
B)
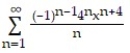
C)
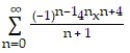
D)
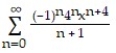

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
78
Use power series operations to find the Taylor series at x = 0 for the given function.
-f(x) =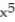
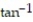 ( 8x)
( 8x)
A)
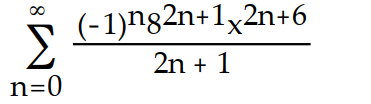
B)
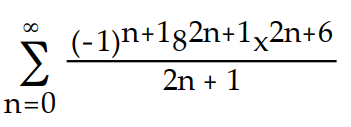
C)
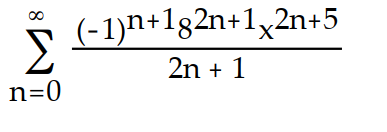
D)
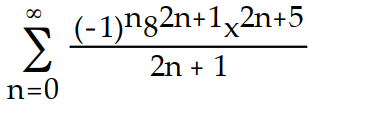
-f(x) =
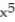
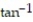 ( 8x)
( 8x)A)
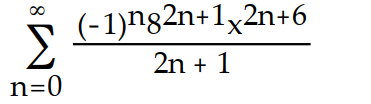
B)
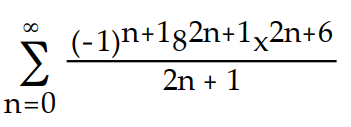
C)
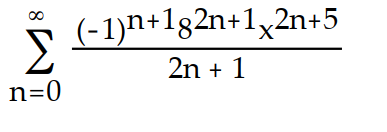
D)
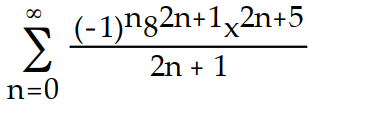

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
79
Use power series operations to find the Taylor series at x = 0 for the given function.
-f(x) =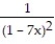
A)
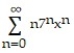
B)
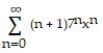
C)
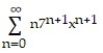
D)
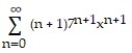
-f(x) =
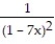
A)
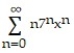
B)
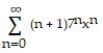
C)
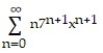
D)
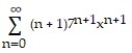

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck
80
Find the first four terms of the binomial series for the given function.
-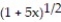
A)
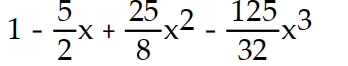
B)
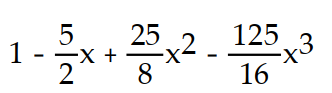
C)
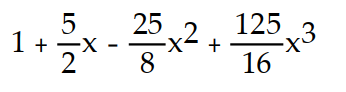
D)
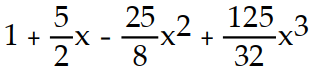
-
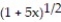
A)
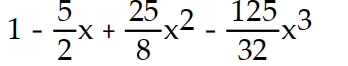
B)
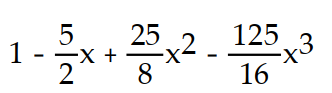
C)
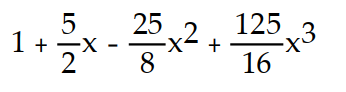
D)
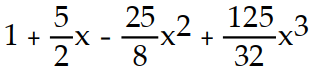

Unlock Deck
Unlock for access to all 103 flashcards in this deck.
Unlock Deck
k this deck


