Exam 11: Power Series
Exam 1: Functions226 Questions
Exam 2: Limits224 Questions
Exam 3: Derivatives367 Questions
Exam 4: Applications of the Derivative228 Questions
Exam 5: Integration166 Questions
Exam 6: Applications of Integration211 Questions
Exam 7: Logarithmic, Exponential, and Hyperbolic Functions85 Questions
Exam 8: Integration Techniques287 Questions
Exam 9: Differential Equations76 Questions
Exam 10: Sequences and Infinite Series173 Questions
Exam 11: Power Series103 Questions
Exam 12: Parametric and Polar Curves169 Questions
Exam 13: Vectors and the Geometry of Space131 Questions
Exam 14: Vector-Valued Functions83 Questions
Exam 15: Functions of Several Variables229 Questions
Exam 16: Multiple Integration299 Questions
Exam 17: Vector Calculus173 Questions
Select questions type
Solve the problem.
-Use a Taylor series to estimate the integral's value to within an error of magnitude less than 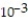 .
. 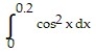
Free
(Multiple Choice)
4.9/5  (38)
(38)
Correct Answer:
A
Find the first four terms of the binomial series for the given function.
-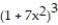
Free
(Multiple Choice)
4.8/5  (30)
(30)
Correct Answer:
C
Find the series' radius of convergence.
-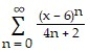
Free
(Multiple Choice)
4.8/5  (40)
(40)
Correct Answer:
B
Find the Taylor polynomial of order 3 generated by f at a.
-f(x) = 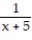 , a = 1
, a = 1
(Multiple Choice)
4.8/5  (28)
(28)
Solve the problem.
-Use a Taylor series to estimate the integral's value to within an error of magnitude less than 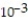 .
. 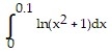
(Multiple Choice)
4.8/5  (41)
(41)
Use power series operations to find the Taylor series at x = 0 for the given function.
-f(x) = 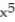
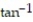 ( 8x)
( 8x)
(Multiple Choice)
4.8/5  (37)
(37)
Find the linear approximating polynomial for the function centered at a.
-f(x) = tan x, a = 0
(Multiple Choice)
4.8/5  (36)
(36)
Find the Taylor polynomial of order 3 generated by f at a.
-f(x) = 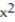 , a = 3
, a = 3
(Multiple Choice)
4.9/5  (38)
(38)
Find the first four terms of the binomial series for the given function.
-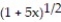
(Multiple Choice)
4.8/5  (37)
(37)
Find the quadratic approximation of f at x = 0.
-f(x) = ln(cos 2x)
(Multiple Choice)
4.9/5  (31)
(31)
Find the Taylor polynomial of order 3 generated by f at a.
-f(x) = 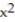 + x + 1, a = 4
+ x + 1, a = 4
(Multiple Choice)
4.8/5  (40)
(40)
Determine the interval of convergence of the power series.
-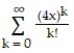
(Multiple Choice)
4.8/5  (24)
(24)
Find the first four terms of the binomial series for the given function.
-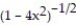
(Multiple Choice)
4.7/5  (38)
(38)
Find the linear approximating polynomial for the function centered at a.
-f(x) = 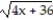 , a = 0
, a = 0
(Multiple Choice)
4.9/5  (24)
(24)
Showing 1 - 20 of 103
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)