Deck 7: Trigonometry and Periodic Functions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/178
Play
Full screen (f)
Deck 7: Trigonometry and Periodic Functions
1
A vacationer sits all day on the corner of a pier in Boston Harbor and notices that at 9 am, when the water level is at its lowest, the water's depth is 2.5 feet. At , the water has risen to its maximum depth of 10.5 feet. If the depth of the water level varies periodically, let be the formula for the depth of the water, in feet, as a function of time , in hours past 9 am. What is the period of the graph of ?
14
2
A ferris wheel is 34 meters in diameter, and must be boarded from a platform that is 1 meters above the ground. The wheel makes one complete revolution every 8 minutes. At the initial time , you are in the position. If gives your height above ground level minutes after the initial time, what is the amplitude of ?
17
3
A ferris wheel is 49 meters in diameter, and must be boarded from a platform that is 1 meters above the ground. The wheel makes one complete revolution every 8 minutes. At the initial time , you are in the position. If gives your height above ground level minutes after the initial time, the midline of is ---------------.
25.5
4
The graph below shows your height in meters minutes after a ferris wheel ride begins. How many minutes are required for one complete revolution of the ferris wheel?
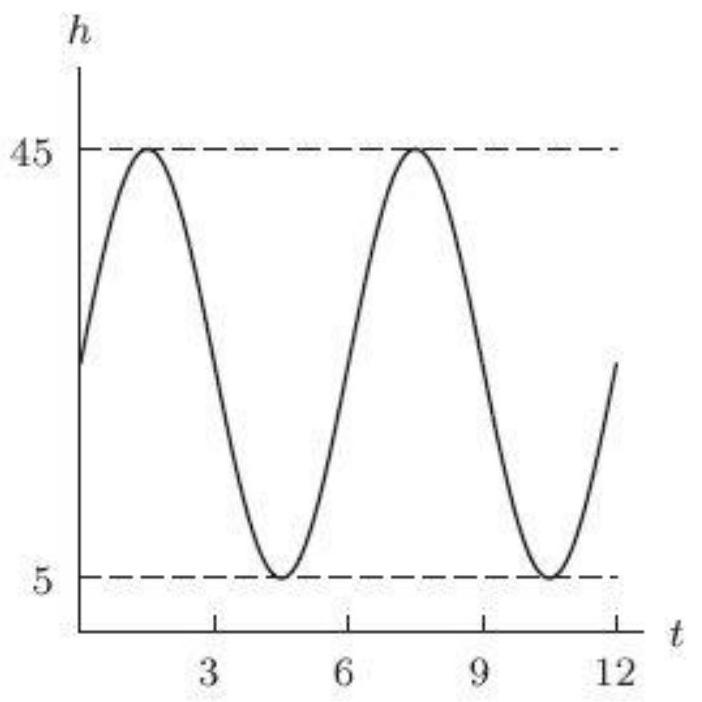


Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
5
The London ferris wheel is 135 meters in diameter and makes one revolution every 30 minutes. Let be the height above ground after minutes of riding. Where is the midline for ?

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
6
The proposed London ferris wheel is 135 meters in diameter and makes one revolution every 30 minutes. Let be the height above ground after minutes of riding. What does represent?
A) The height on a wheel which is 2 times larger in diameter than the London one.
B) The height of a person who boarded the London ferris wheel 2 minutes before you.
C) The height on a ferris wheel that runs 2 times faster than the London one.
D) The height on the London ferris wheel with a loading platform 2 meters off the ground.
A) The height on a wheel which is 2 times larger in diameter than the London one.
B) The height of a person who boarded the London ferris wheel 2 minutes before you.
C) The height on a ferris wheel that runs 2 times faster than the London one.
D) The height on the London ferris wheel with a loading platform 2 meters off the ground.

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
7
Does the following function appear to be periodic with period ?
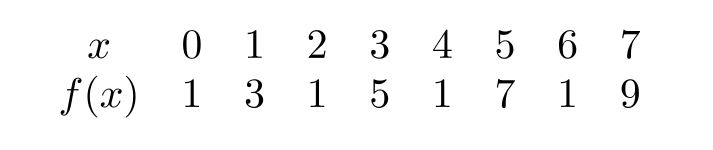
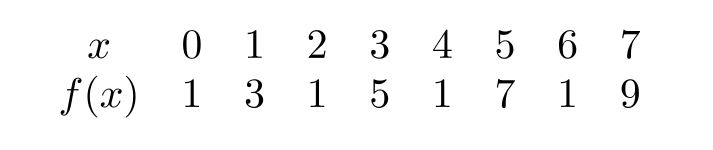

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
8
Does the following function appear to be periodic with period less than or equal to 4 ?
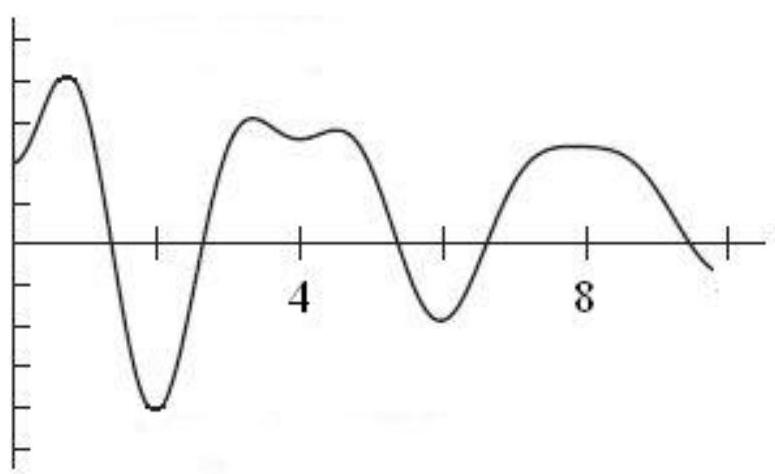


Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
9
Estimate the period of the following periodic function.
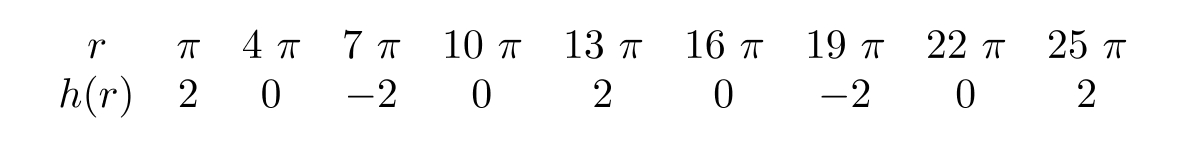
A)
B)
C) -2
D) -4
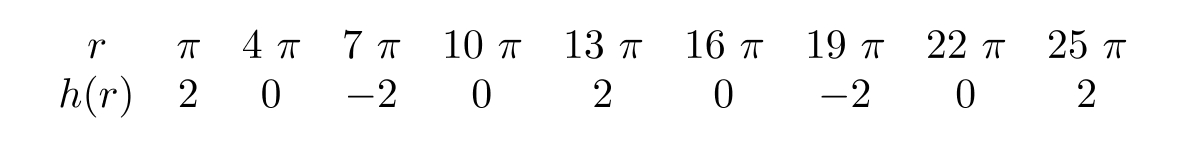
A)
B)
C) -2
D) -4

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
10
Estimate the period of the following periodic function.
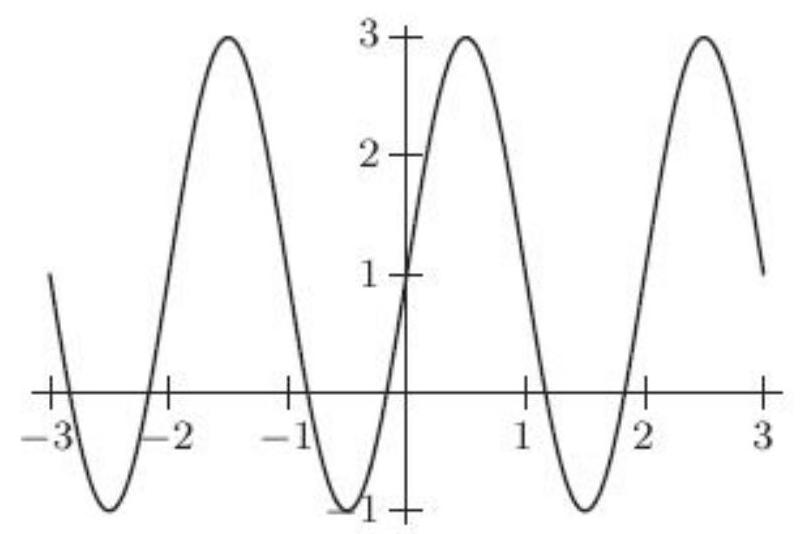


Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
11
Suppose and . What is if is periodic with period ? Your answer will have in it.

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
12
Suppose and . What is if is linear? Your answer will have in it.

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
13
Suppose you are on a ferris wheel (that turns in a counter clockwise direction) and that your height, in meters, above the ground at time , in minutes, is given by . How many meters above the ground are you at time

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
14
Suppose you are on a ferris wheel (that turns in a counter clockwise direction) and that your height, in meters, above the ground at time , in minutes, is given by . Your position on the wheel be at time is ---------oclock.

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
15
Suppose you are on a ferris wheel (that turns in a counter clockwise direction) and that your height, in meters, above the ground at time , in minutes, is given by . How many meters is the radius of the wheel?

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
16
An animal population in a national park dropped from a high of 165,000 in 1943 to a low of 63,000 in 1989, and has risen since then. Scientists hypothesize that the population follows a sinusoidal cycle affected by predation and other environmental conditions, and that the caribou will again reach their previous high. Predict the next year when the population will again be 165,000 .

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
17
Graph a function with midline 1 , amplitude 2, and period 4 . Show at least two full periods.

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
18
Suppose the table below is for a periodic function with period 3:
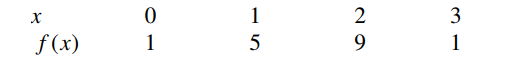
What is the next integer value at which ?
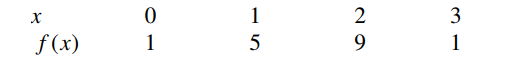
What is the next integer value at which ?

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
19
Suppose the table below is for a periodic function with period 3:
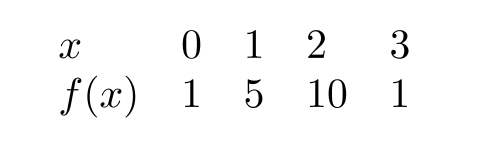
Evaluate .
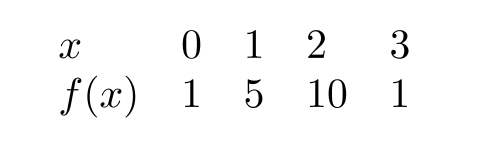
Evaluate .

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
20
Which of the following graphs have period 5 and amplitude 2 ?
A)
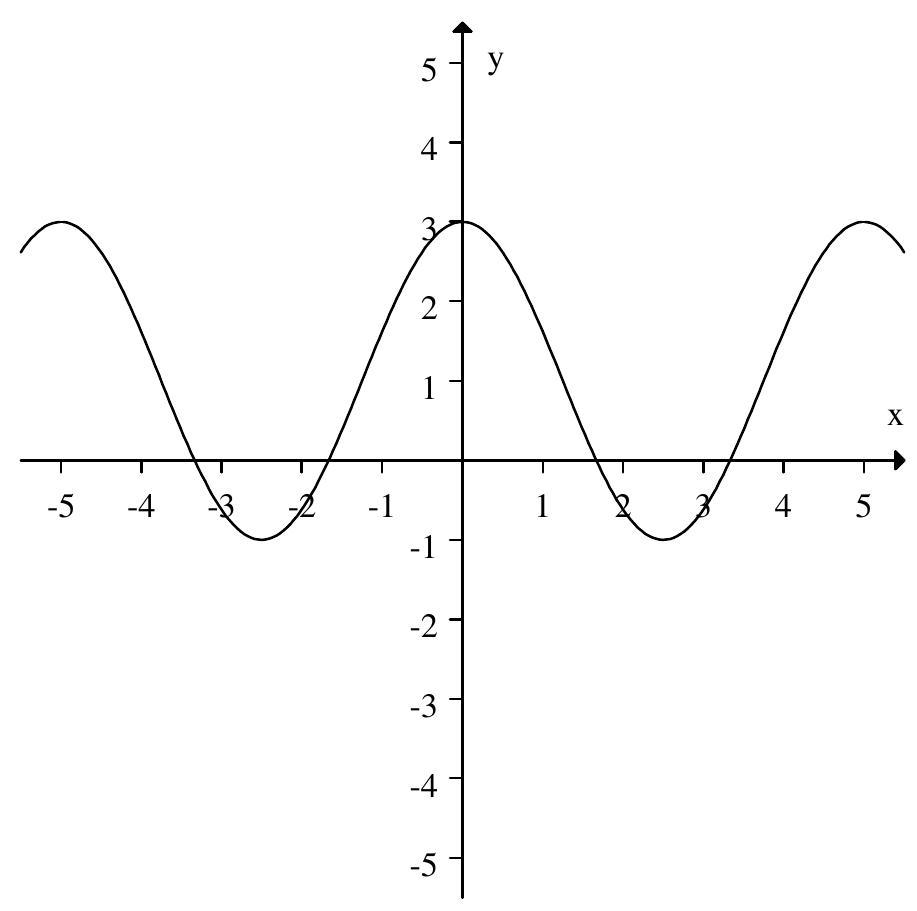
B)
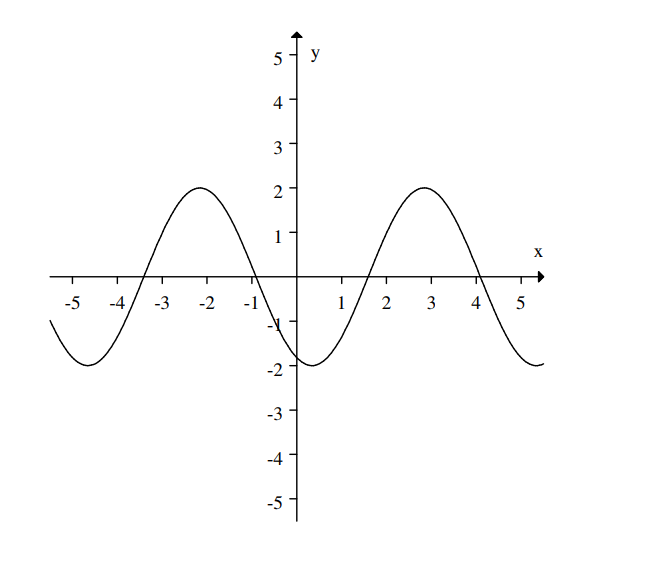
C)
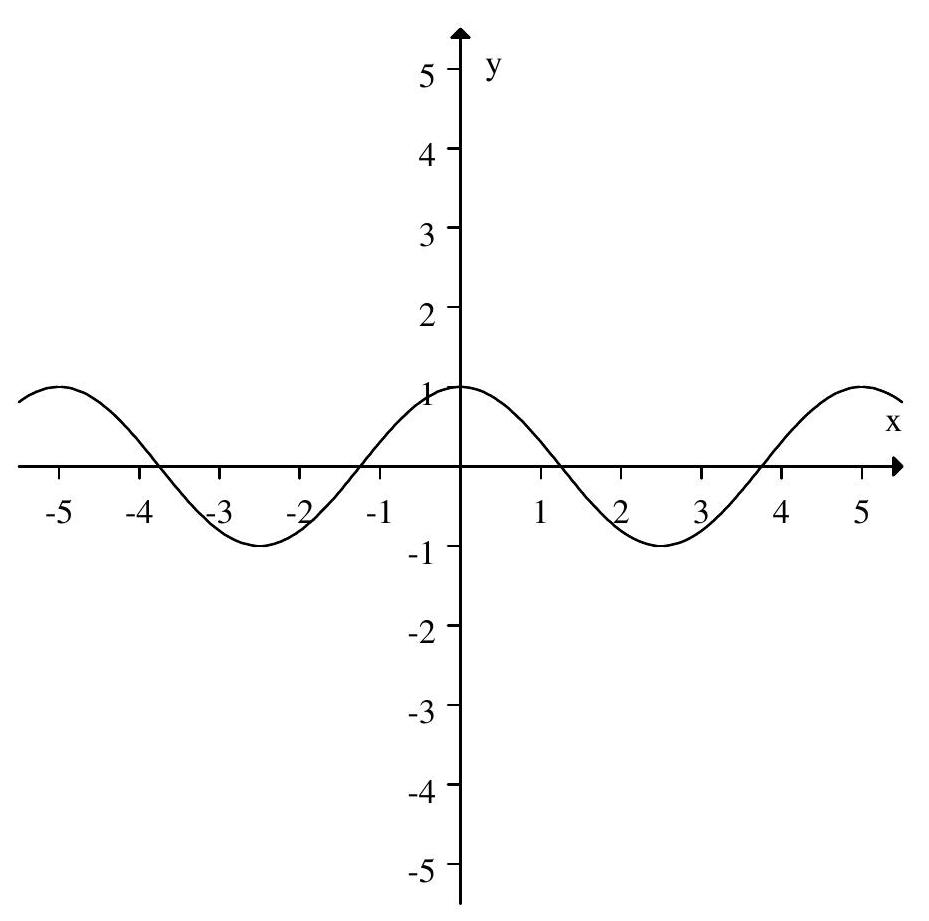
D)
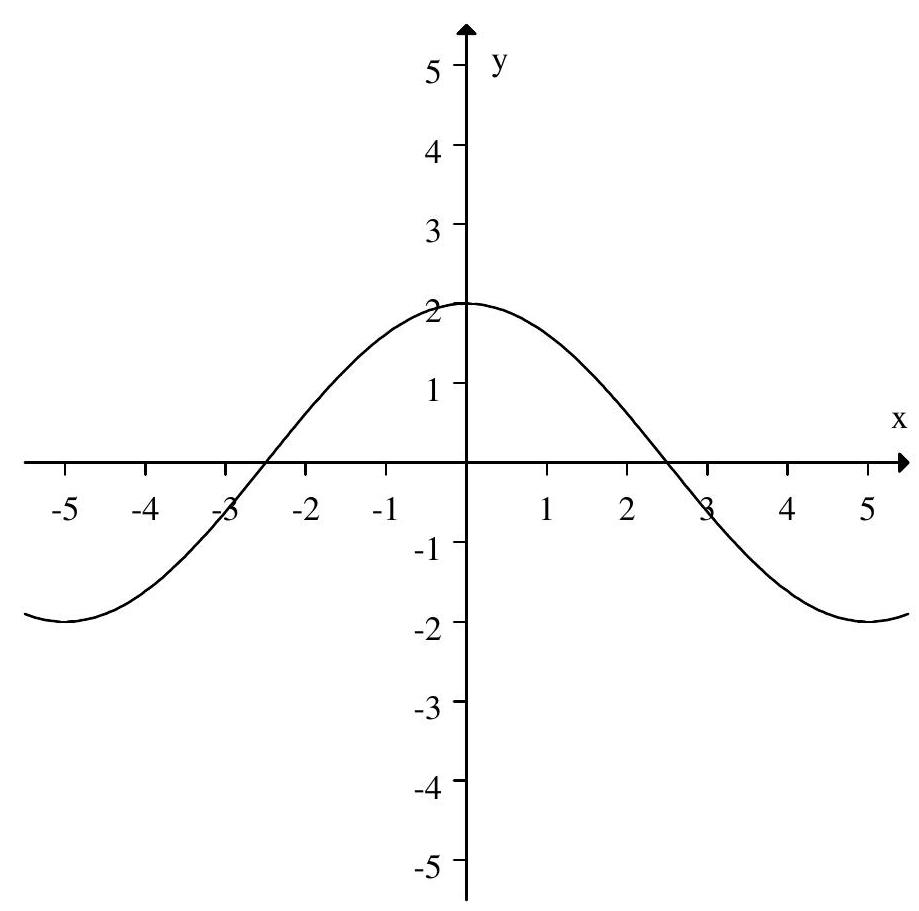
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
21
The height above ground for a skydiver seconds after exiting the plane is given in the table.
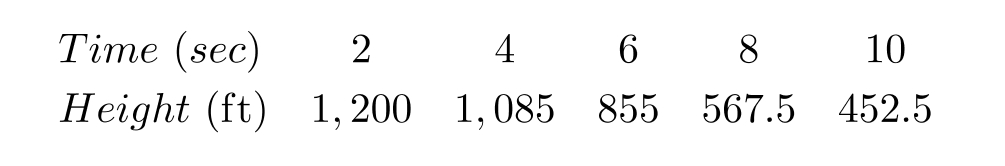
Find the skydiver's average vertical speed between 6 and 8 seconds.
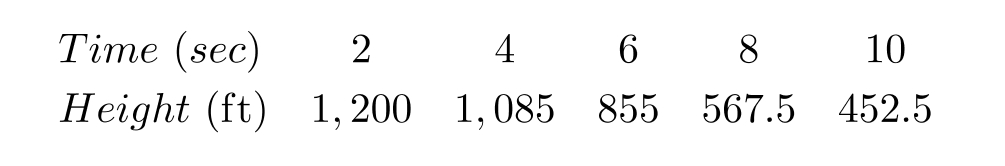
Find the skydiver's average vertical speed between 6 and 8 seconds.

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
22
A rocket is launched and its height above ground is given in the table.
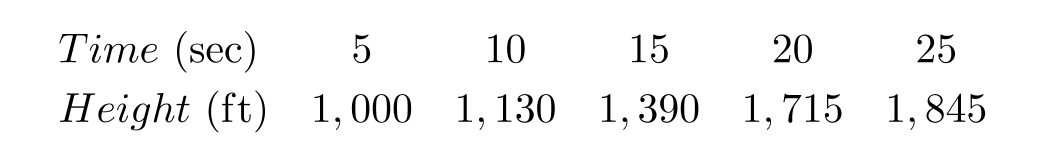
Find the rocket's average vertical speed between 20 and 25 seconds.
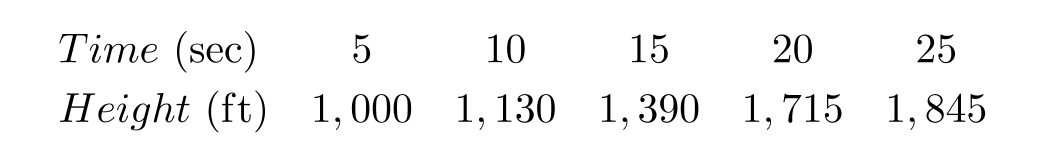
Find the rocket's average vertical speed between 20 and 25 seconds.

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
23
Given this graph of the distance of a pendulum from a wall,
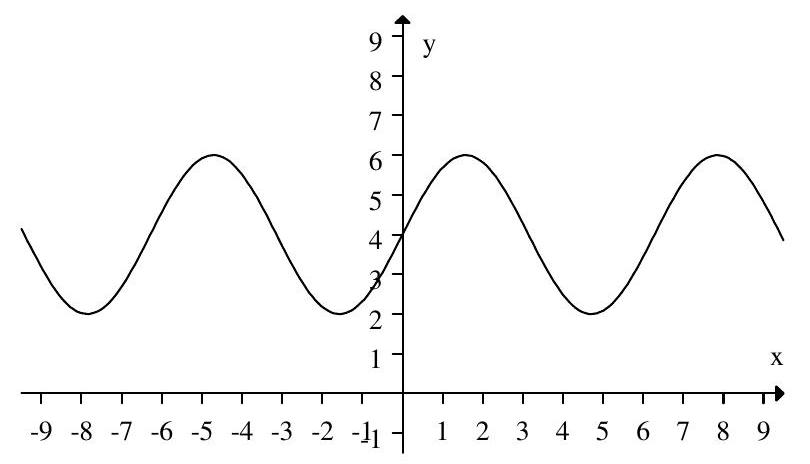
what is the resting position of the pendulum (at the bottom of the swing) from the wall?

what is the resting position of the pendulum (at the bottom of the swing) from the wall?

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
24
Given this graph of the distance of a pendulum from a wall,
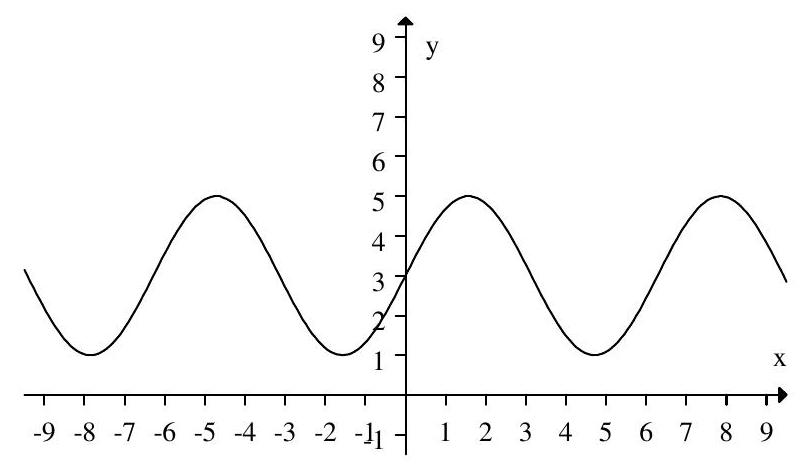
how far does the pendulum swing from the resting position?

how far does the pendulum swing from the resting position?

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
25
Find the point on the unit circle determined by the angle . (Round to three decimal places.)

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
26
Find the angle that determines the point on the unit circle. (Round to the nearest degree.)

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
27
Find the reference angle for .

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
28
Find the point on a circle with radius 4.5 determined by the angle . (Round to three decimal places.)

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
29
What angle corresponds to 1.5 rotations around the unit circle?

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
30
In the following figure, the coordinates of are . The angle Round to the nearest whole degree.
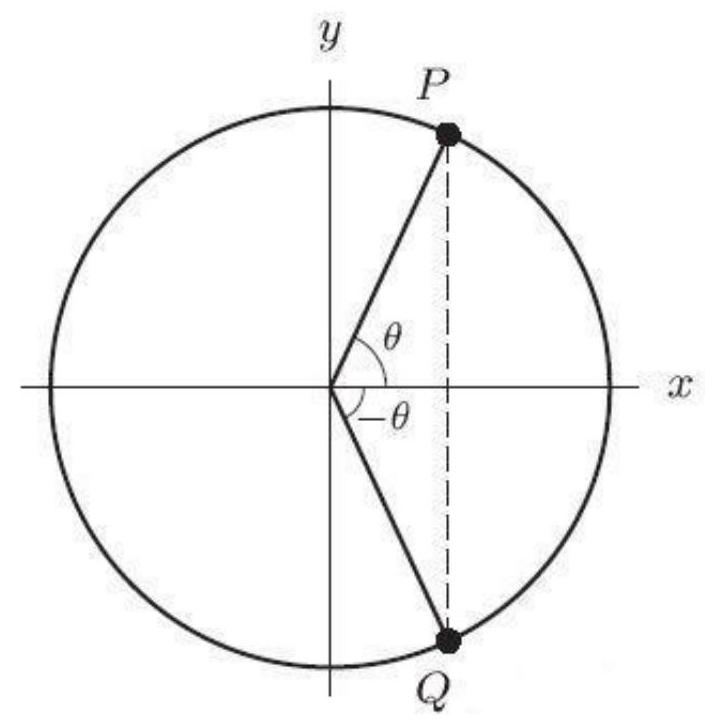


Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
31
In the following figure, the coordinates of are . The coordinates of are ( --------------,-----------). Round to 2 decimal places.
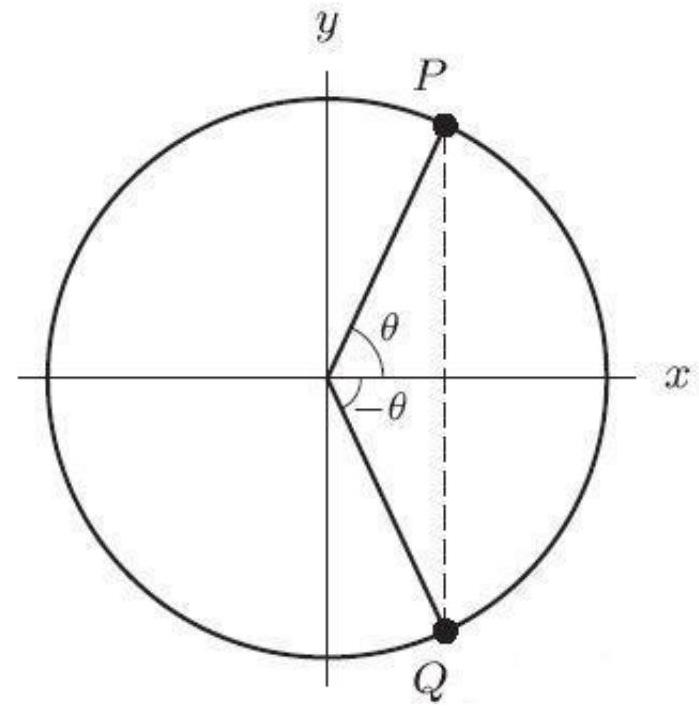


Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
32
In the following figure, the coordinates of are . The angle ----------° Round to the nearest whole number.
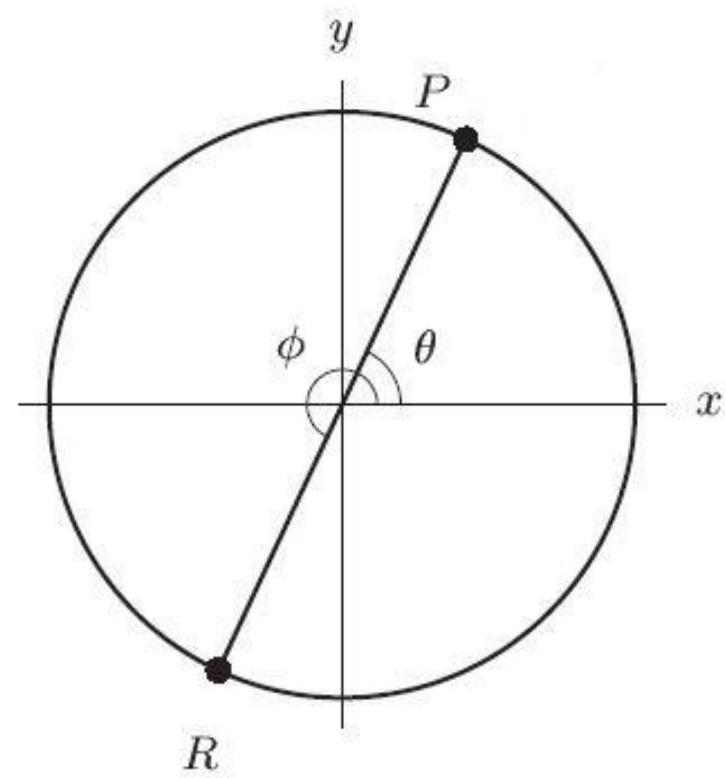


Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
33
In the following figure, the coordinates of are . The angle -------------° Round to the nearest whole number.
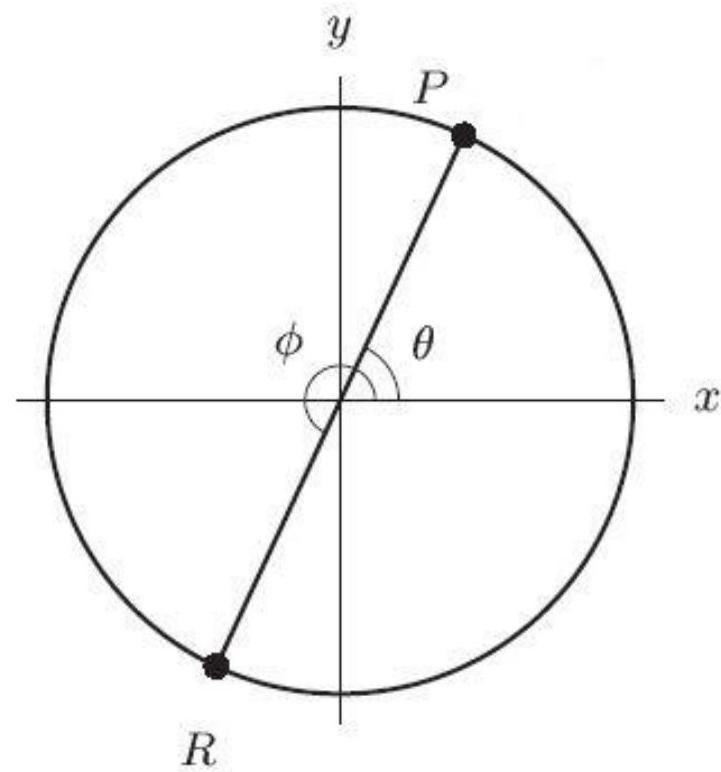


Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
34
In the following figure, the coordinates of are . The coordinates of are (-----------------,-------------- ). Round to the nearest whole number.
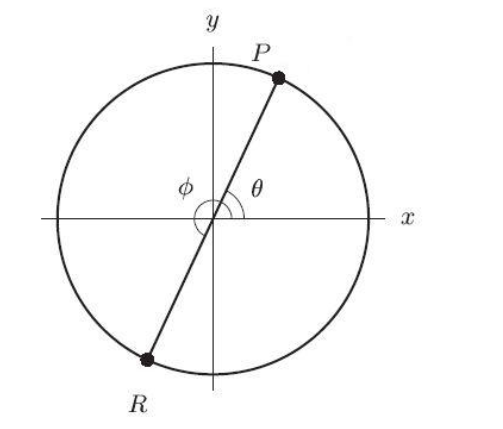


Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
35
In the following figure, the coordinates of are . The angle ------------- ° Round to the nearest degree.


Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
36
2.25 rotations around the unit circle corresponds to ------------°

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
37
The coordinates of the point on the unit circle at the angle are . Round each coordinate to 3 decimal places.

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
38
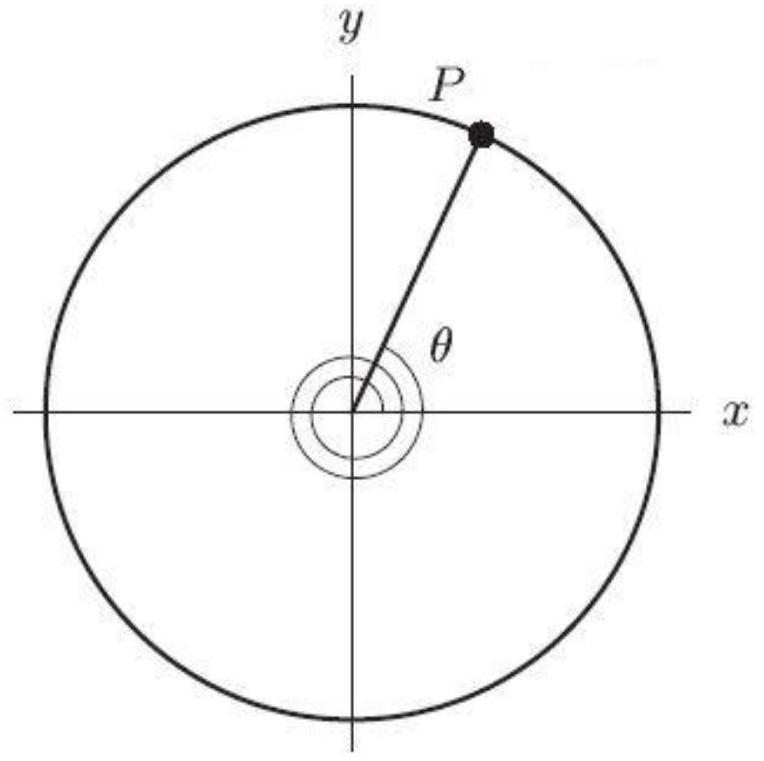
In the following figure, the circle shown is the unit circle. The coordinates of are ( ---------------,-----------). Round to 2 decimal places.


Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
39
In the following figure, the circle shown is the unit circle. What is the horizontal distance from to the -axis? Round to 2 decimal places.
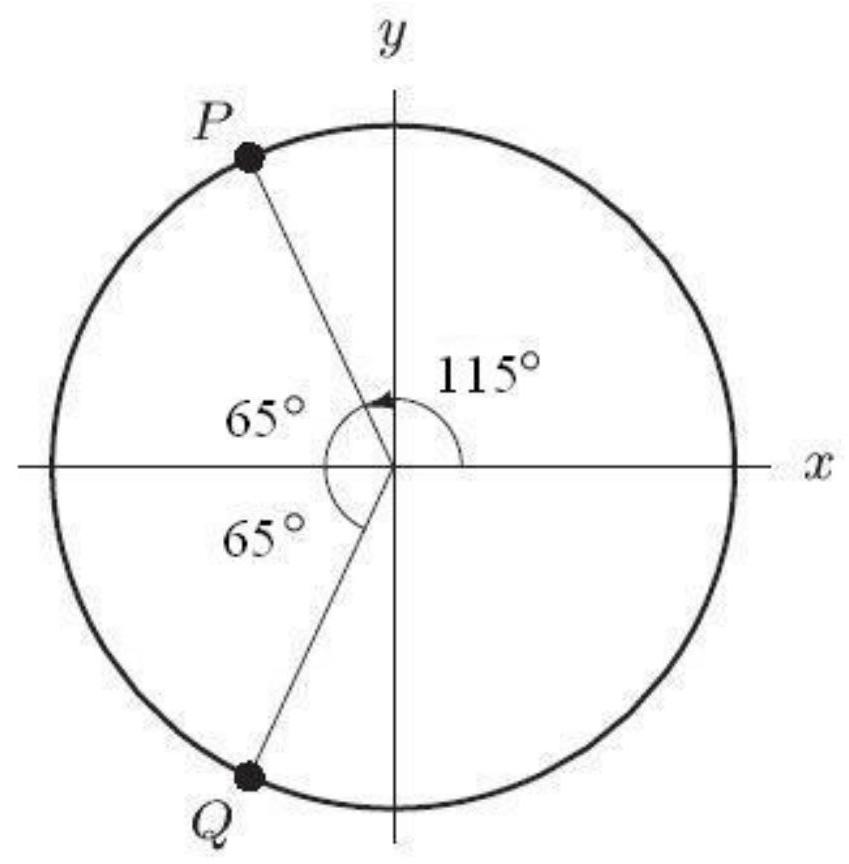


Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
40
In the following figure, what is the length of segment ?
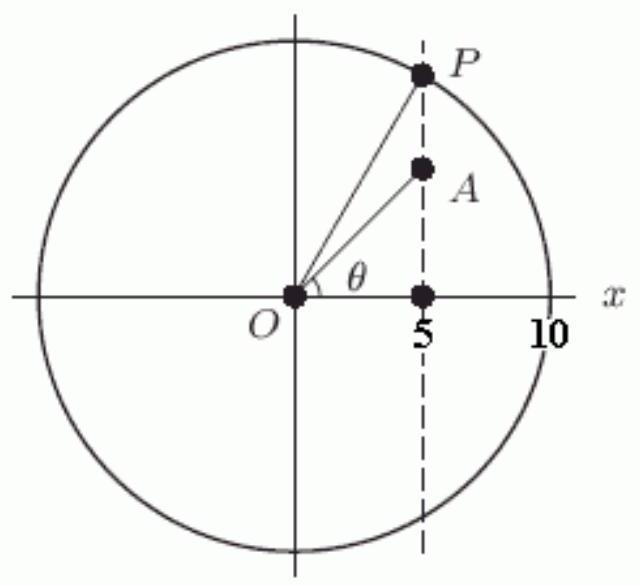
A)
B)
C)
D)

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
41
A 16 foot ladder leans against the wall, forming a angle with the ground. How many feet from the wall is the foot of the ladder? Round to 2 decimal places.

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
42
In order to measure its height, you stand 75 feet from a tree. The angle of sight is . How tall is the tree? Round your answer to the nearest hundredth of a foot.

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
43
If the -value for the point on the unit circle with angle is 0.39 , find and . Round your answers to three decimal places, if necessary.

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
44
If the -value for the point on the unit circle with angle is 0.39 , find and . Round your answers to three decimal places, if necessary.

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
45
Find the coordinates of the point on the unit circle with angle if . Round each coordinate to 3 decimal places.

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
46
Find the coordinates of the point on the unit circle with angle if . Round each coordinate to 3 decimal places.

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
47
If angle lies in Quadrant II, name the quadrant in which the following angles lie :
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
48
Consider the following figure. If , and , find and . Round your answers to 2 decimal places, if necessary.
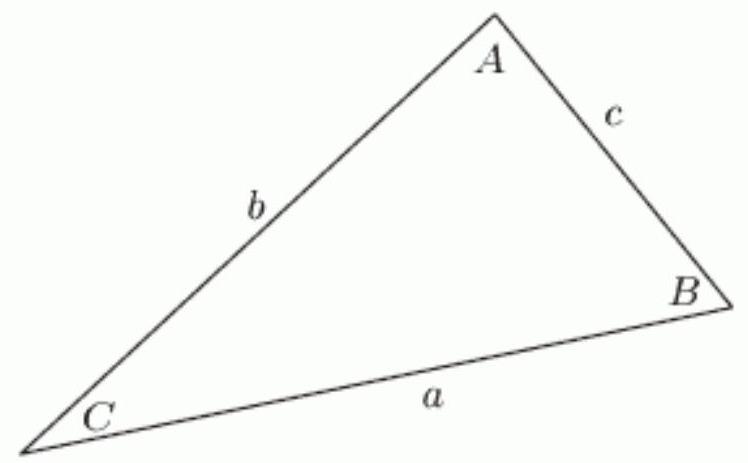


Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
49
Consider the following figure. If , and , find and . Round your answers to 2 decimal places, if necessary.
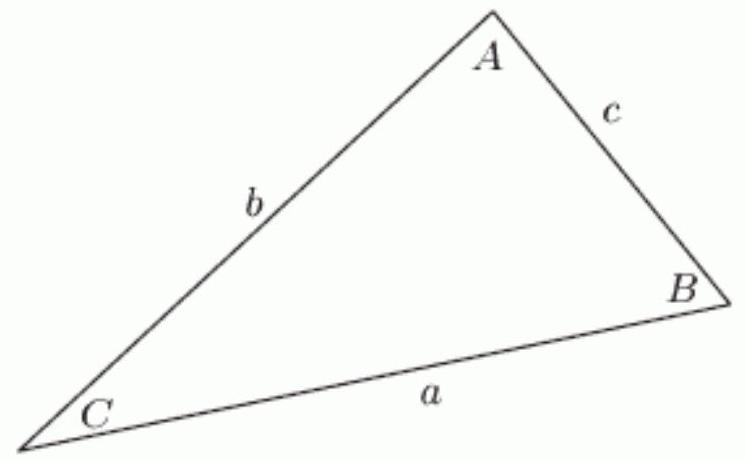


Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
50
The coordinates of the point on a circle of radius 5 at the angle are (---------------,-------------). Round each coordinate to 3 decimal places.

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
51
Find the coordinates of the point at angle on a circle of radius 7.1. Round each coordinate to 3 decimal places, if necessary.

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
52
What is for ?

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
53
The following figure shows the path taken by the left front tire of a car as it changes direction sharply from due north to due east. The turning radius of the car is 20 feet, and the two front wheels are 56 inches apart. How many feet does the left front wheel travel from to ? Round to 1 decimal place.
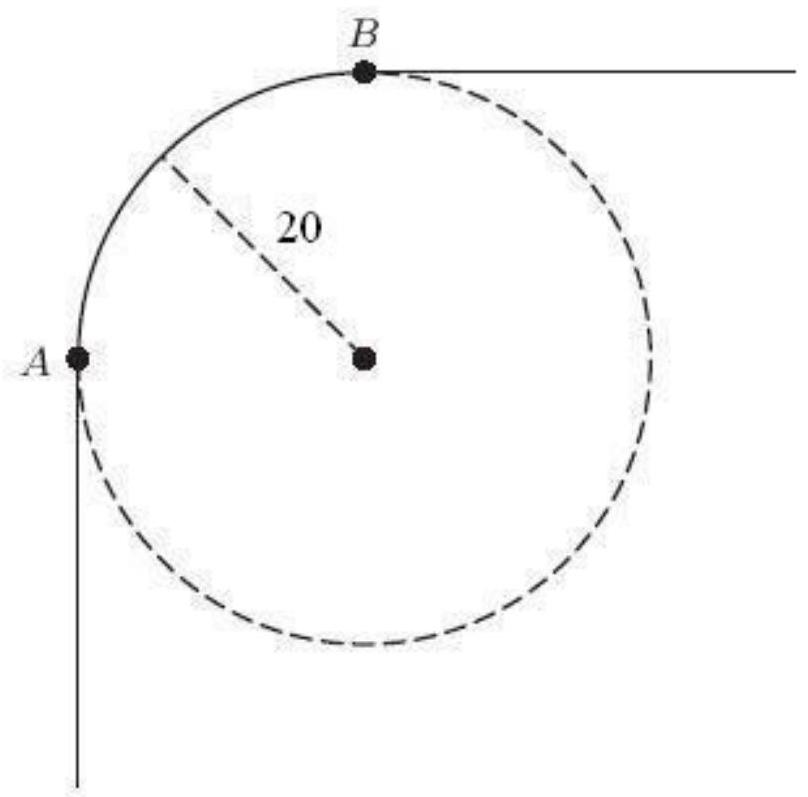


Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
54
The following figure shows the path taken by the left front tire of a car as it changes direction sharply from due north to due east. The turning radius of the car is 18 feet, and the two front wheels are 57 inches apart. While the left front wheel travels from to , how many feet does the right front wheel travel? Round to 1 decimal place.
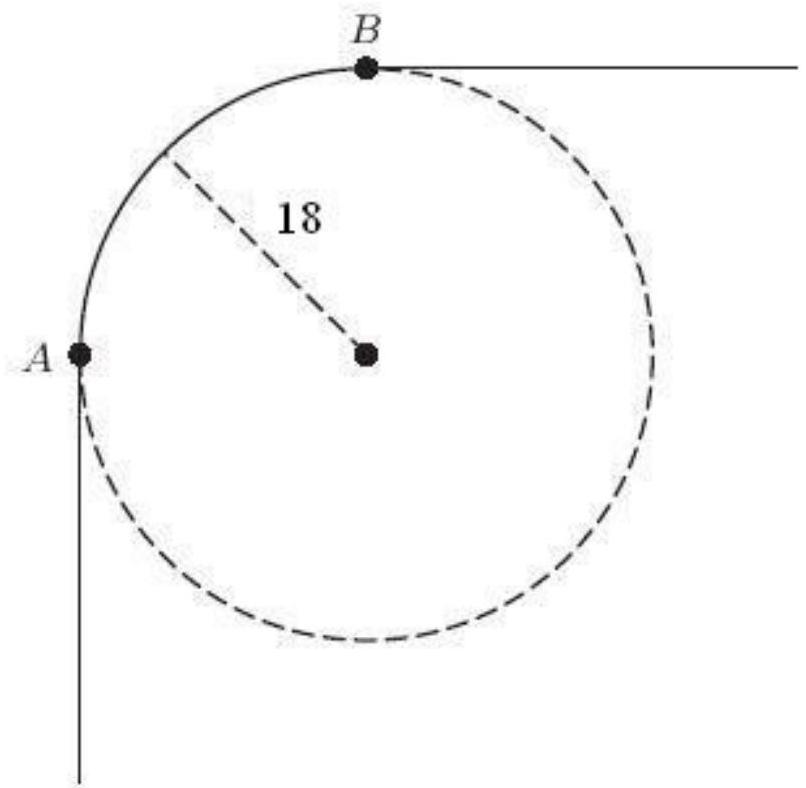


Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
55
The minute hand on a watch is 0.5 inches long. How many inches does the tip of the minute hand travel as the hand turns through ? Round to 2 decimal places.

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
56
The minute hand on a clock is 3.6 inches long. How many inches per minute does the tip of the minute hand travel? Round to 3 decimal places.

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
57
In the revolving door in the figure below, each panel is 1.1 meters long. How many meters is the arc length between and ? Round to 2 decimal places.
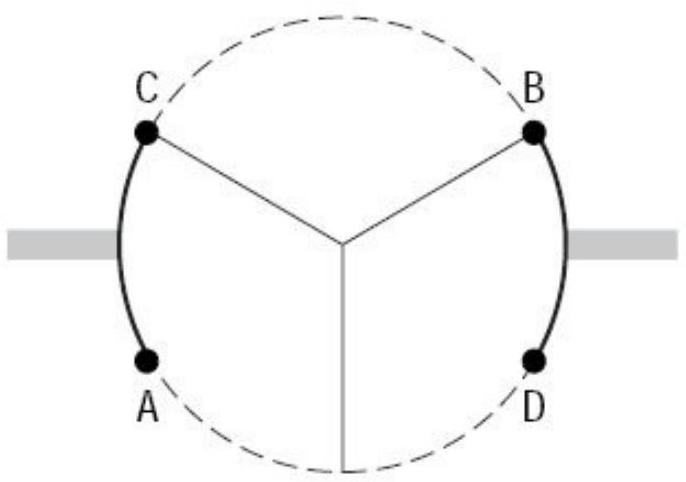


Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
58
Without a calculator, what is the exact value of ?

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
59
What is the reference angle for ?
A) 0
B)
C)
D)
A) 0
B)
C)
D)

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
60
The arc length corresponding to on a circle of radius 2.5 is ------------- . Round to 2 decimal places.

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
61
The angle is equivalent to ------------ radians. Round your answer to 2 decimal places.

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
62
The angle radians is equivalent to --------------°

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
63
0.5 rotations around the unit circle corresponds to -------------- radians.

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
64
What is the length of an arc cut off by an angle of in a circle of radius 2.5 meters? Give your answer correct to 3 decimal places.

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
65
An ant starts at the point and walks 1.5 units around the unit circle in a clockwise direction. Find the and coordinates (accurate to 2 decimal places) of the final location of the ant.

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
66
Find the sign of the following:
a)
b)
a)
b)

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
67
The number is positive.

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
68
A wheel has radius 6 inches and spins at a rate of 11 revolutions per second. A red dot is painted on the outermost part of the wheel. How far (in inches) has the dot traveled in 7 seconds? Round your answer to 3 decimal place.

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
69
A wheel has radius 6 inches and spins at a rate of 766 degrees per second. A red dot is painted on the outermost part of the wheel. How far (inches) has the dot traveled in 7 seconds? Round your answer to 3 decimal places.

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
70
Which is larger: or ?

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
71
Which is larger: or ?

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
72
The coordinates of the point on a circle of radius 5 at the angle are ( ------------,------------). Round each coordinate to 3 decimal places.

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
73
Without a calculator, find the exact value of .

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
74
Find the coordinates of the point at angle on a circle of radius 7.1. Round each coordinate to 3 decimal places, if necessary.

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
75
A circle of radius 3 is centered at the origin. Point A lies on the circle at angle . Point lies outside the circle and has coordinates . What is the distance between these two points? Round your answer to 2 decimal places.

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
76
What angle in radians corresponds to 2.3 rotations around the unit circle? Round to 2 decimal places.

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
77
Find the arc length corresponding to an angle of radians on a circle of radius 3.9.
Round to 2 decimal places.
Round to 2 decimal places.

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
78
The point in the following figure is at the lowest point on the sine-curve. As increases, does the value of increase, decrease, or stay the same?
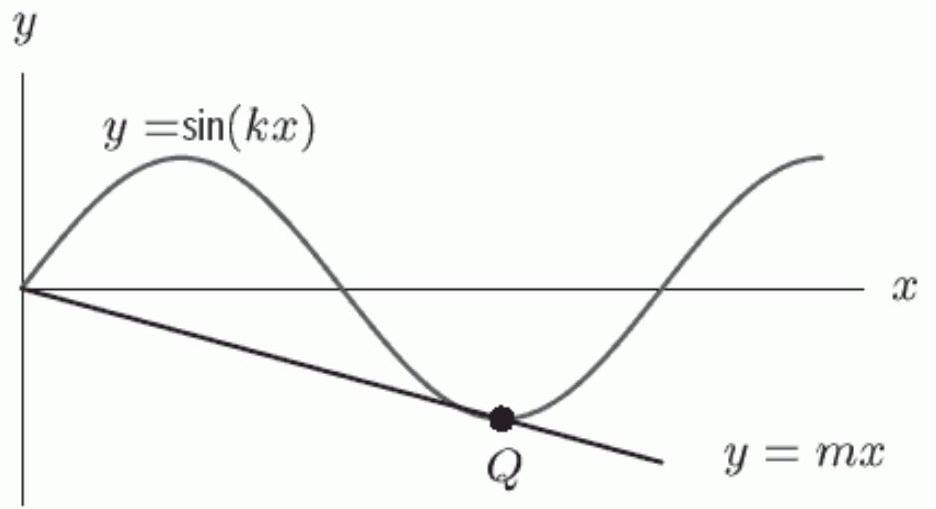


Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
79
City is a modest tourist town, which means that its population undergoes a seasonal variation. In January, it dips down to 4,000 people. By July, with the warm weather, its population climbs to around 5,000 people. This trend repeats every year. City , on the other hand, is a small town not far from City . Its population has been growing extremely rapidly ever since the arrival of several large industrial plants. There were only 3,500 people living in City on January 1, 2004, but its population has been growing by every year thereafter. At how many different points in time will the population of City equal the population of City ?

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck
80
City is a modest tourist town, which means that its population undergoes a seasonal variation. In January, it dips down to 6000 people. By July, with the warm weather, its population climbs to around 8000 people. This trend repeats every year. City , on the other hand, is a small town not far from City . Its population has been growing extremely rapidly ever since the arrival of several large industrial plants. There were only 5500 people living in City on January 1, 2000, but its population has been growing by every year thereafter. During which year did population of City last equal the population of City ?

Unlock Deck
Unlock for access to all 178 flashcards in this deck.
Unlock Deck
k this deck


