Exam 7: Trigonometry and Periodic Functions
Exam 1: Linear Functions and Change148 Questions
Exam 2: Functions138 Questions
Exam 3: Quadratic Functions46 Questions
Exam 4: Exponential Functions94 Questions
Exam 5: Logarithmic Functions87 Questions
Exam 6: Transformations of Functions and Their Graphs85 Questions
Exam 7: Trigonometry and Periodic Functions178 Questions
Exam 8: Triangle Trigonometry and Polar Coordinates43 Questions
Exam 9: Trigonometric Identities, Models, and Complex Numbers106 Questions
Exam 10: Compositions, Inverses, and Combinations of Functions69 Questions
Exam 11: Polynomial and Rational Functions145 Questions
Exam 12: Vectors and Matrices104 Questions
Exam 13: Sequences and Series81 Questions
Exam 14: Parametric Equations and Conic Sections128 Questions
Select questions type
An ant walks up a ramp at an incline of . If, after 2 minutes, his vertical distance from the ground is 13 inches, how fast was the ant travelling in inches per minute? Round your answer to 2 decimal places.
Free
(Short Answer)
4.7/5  (33)
(33)
Correct Answer:
34.07 inches per minute
Find , an angle in a right triangle, if . Give your answer to 3 decimal places.
Free
(Short Answer)
4.8/5  (27)
(27)
Correct Answer:
Does the following function appear to be periodic with period ?
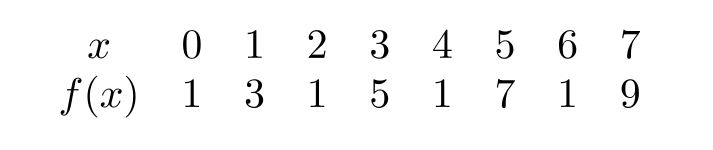
Free
(True/False)
4.9/5  (29)
(29)
Correct Answer:
False
In the following figure, the coordinates of are . The coordinates of are ( --------------,-----------). Round to 2 decimal places.
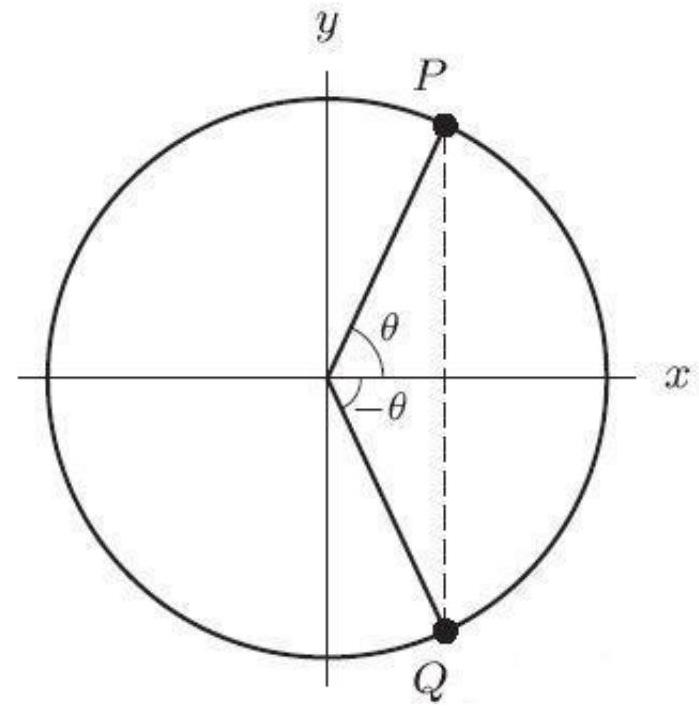
(Short Answer)
4.7/5  (33)
(33)
Find the following exactly using the figure given if and . Express your answers as unsimplified radicals when appropriate.
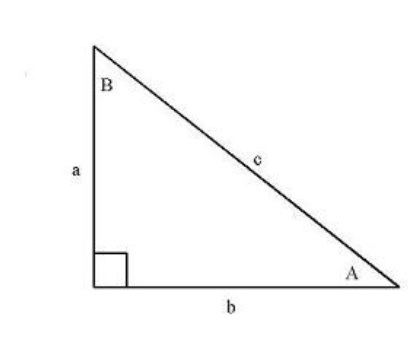 A)
B)
C)
D)
E)
F)
A)
B)
C)
D)
E)
F)
(Essay)
4.8/5  (37)
(37)
City is a modest tourist town, which means that its population undergoes a seasonal variation. In January, it dips down to 4,000 people. By July, with the warm weather, its population climbs to around 5,000 people. This trend repeats every year. City , on the other hand, is a small town not far from City . Its population has been growing extremely rapidly ever since the arrival of several large industrial plants. There were only 3,500 people living in City on January 1, 2004, but its population has been growing by every year thereafter. At how many different points in time will the population of City equal the population of City ?
(Short Answer)
4.7/5  (35)
(35)
Which of the following graphs have period 5 and amplitude 2 ?
(Multiple Choice)
4.7/5  (39)
(39)
Point A lies on a circle of radius 2.5 at angle . Point lies on a circle of radius 3 at angle . If both circles are centered at the origin, which point has the least -value?
(Short Answer)
4.8/5  (34)
(34)
Consider the following figure. If , and , find and . Round your answers to 2 decimal places, if necessary.
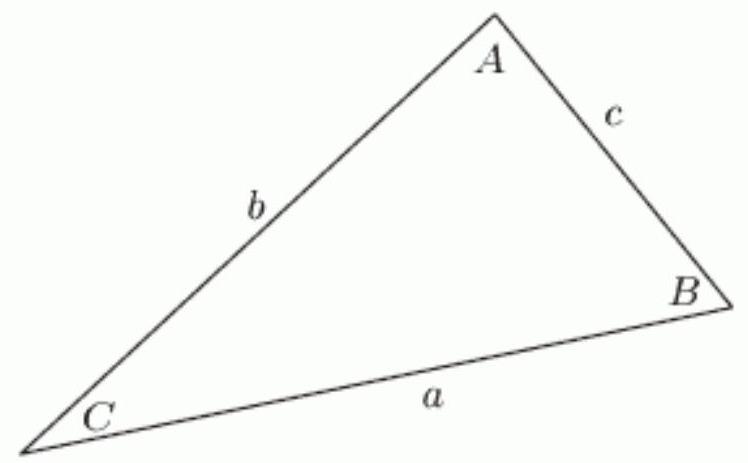
(Short Answer)
4.8/5  (27)
(27)
In the revolving door in the figure below, each panel is 1.1 meters long. How many meters is the arc length between and ? Round to 2 decimal places.
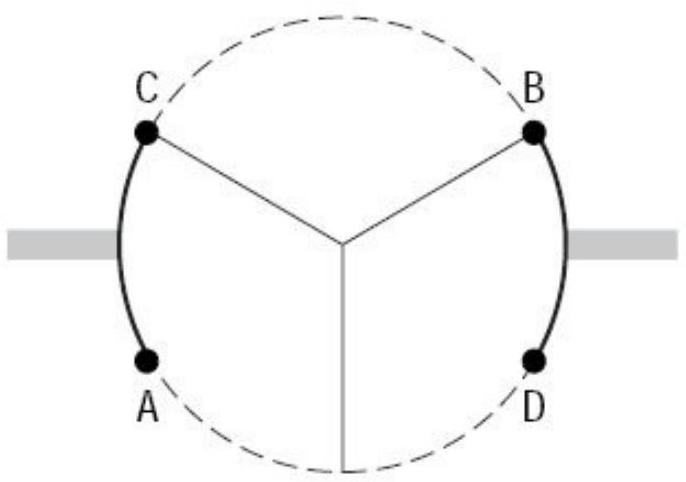
(Short Answer)
4.8/5  (36)
(36)
Estimate the period, midline, and amplitude of the periodic function with the following graph :
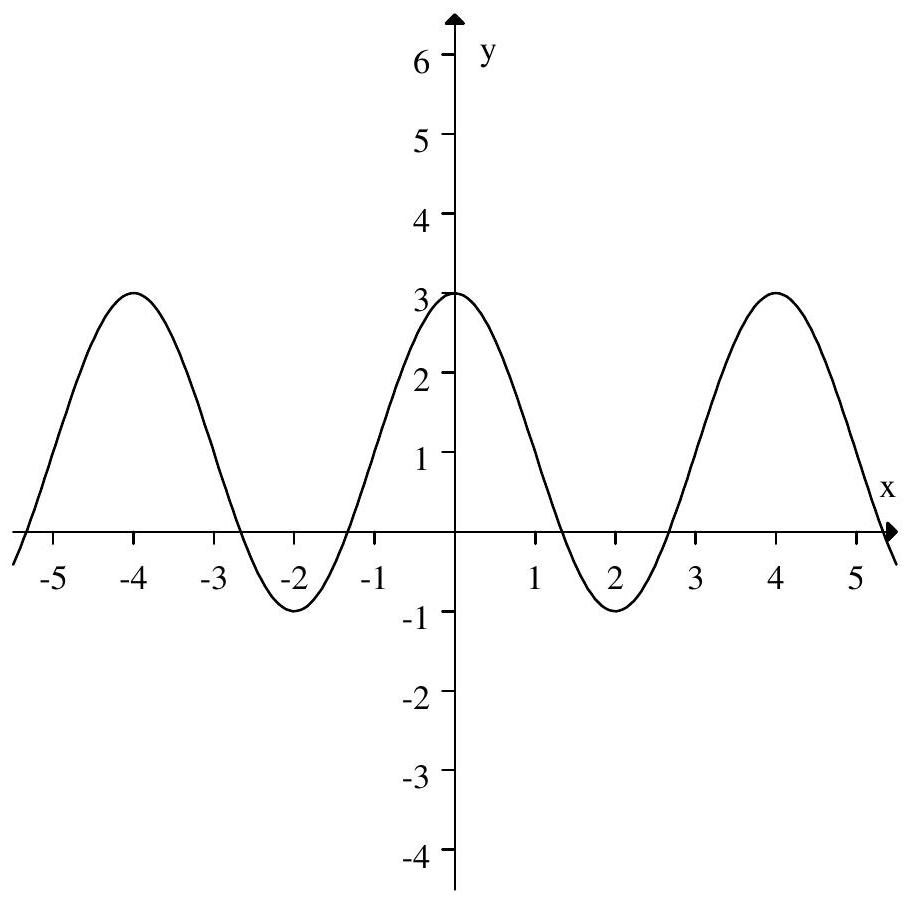
(Short Answer)
4.8/5  (37)
(37)
A wheel has radius 6 inches and spins at a rate of 766 degrees per second. A red dot is painted on the outermost part of the wheel. How far (inches) has the dot traveled in 7 seconds? Round your answer to 3 decimal places.
(Short Answer)
4.9/5  (38)
(38)
Without a calculator, find the exact value of . If it is undefined, enter "undefined".
(Short Answer)
4.7/5  (44)
(44)
Two ships start at the same port. Ship A travels due east at . Ship B travels due north. After 3 hours, the ships are 56.60 miles apart. How fast was ship B traveling? Round your answer to the nearest whole number.
(Short Answer)
4.8/5  (31)
(31)
If the -value for the point on the unit circle with angle is 0.39 , find and . Round your answers to three decimal places, if necessary.
(Short Answer)
4.8/5  (30)
(30)
Solve for , an angle in a right triangle, if . Give the answer correct to 3 decimal places.
(Short Answer)
4.9/5  (36)
(36)
Showing 1 - 20 of 178
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)