Deck 10: Compositions, Inverses, and Combinations of Functions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/69
Play
Full screen (f)
Deck 10: Compositions, Inverses, and Combinations of Functions
1
If , what is the value of in the following tables?


9
2
Let and . Evaluate .
4
3
The functions and are defined by the graph below. The dashed graph is and the solid graph is .
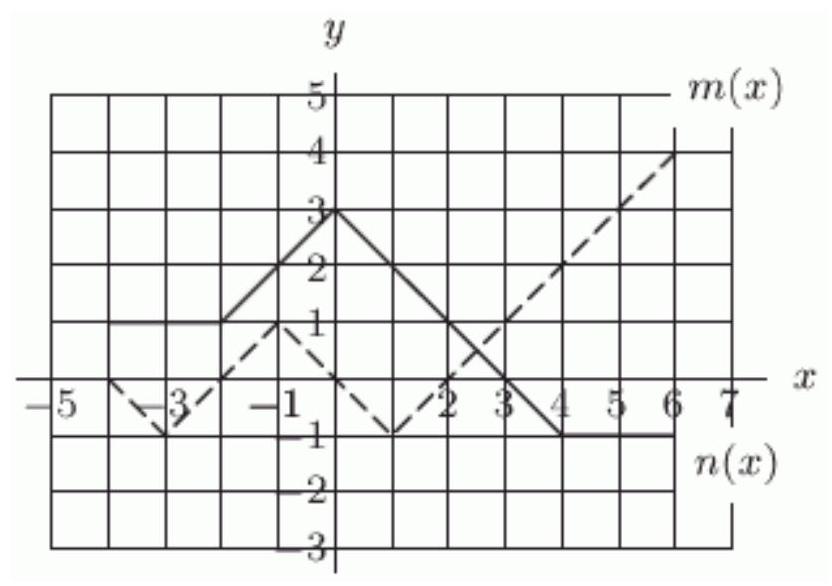
Evaluate .

Evaluate .
-1
4
If , which of the following could be true? Mark all that apply.
A)
B)
C)
D)
E)
F)
A)
B)
C)
D)
E)
F)

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
5
The functions and are defined by the graph below. The dashed graph is and the solid graph is .
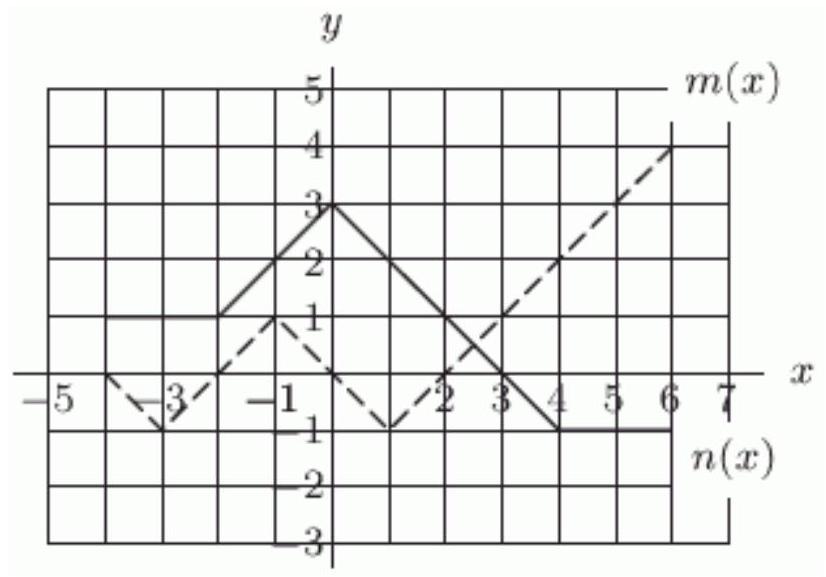
If , what is ?

If , what is ?

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
6
Given the graphs of and below, evaluate .
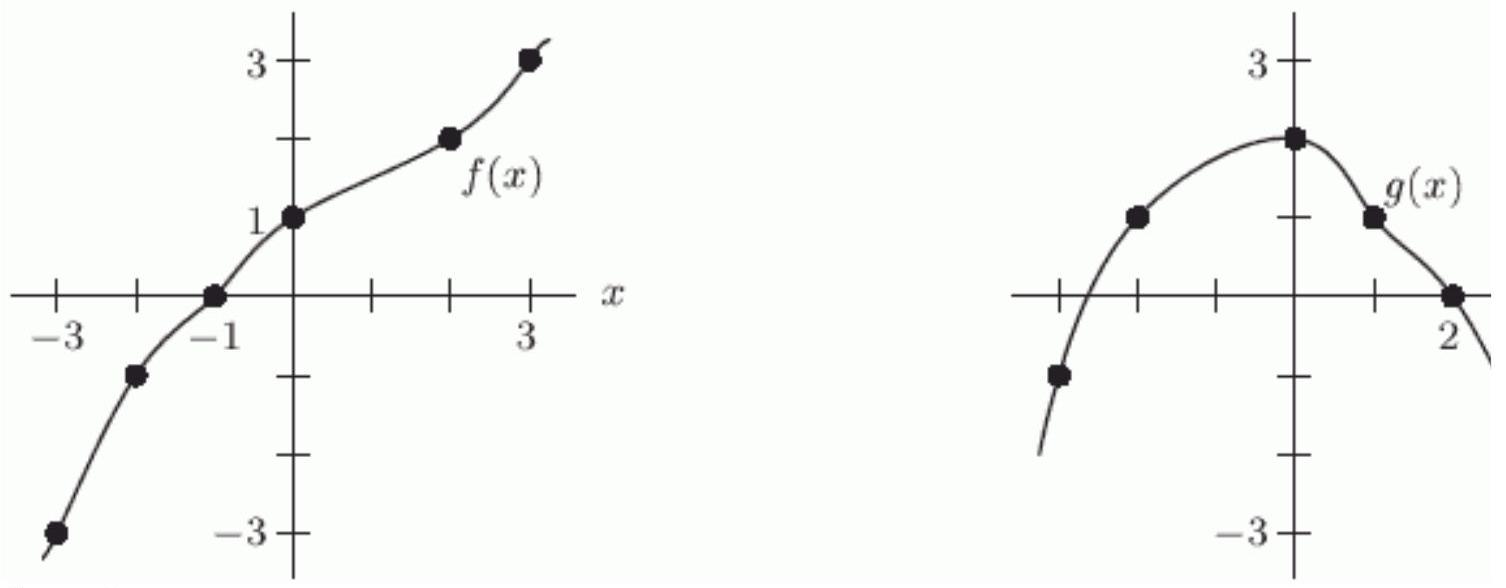
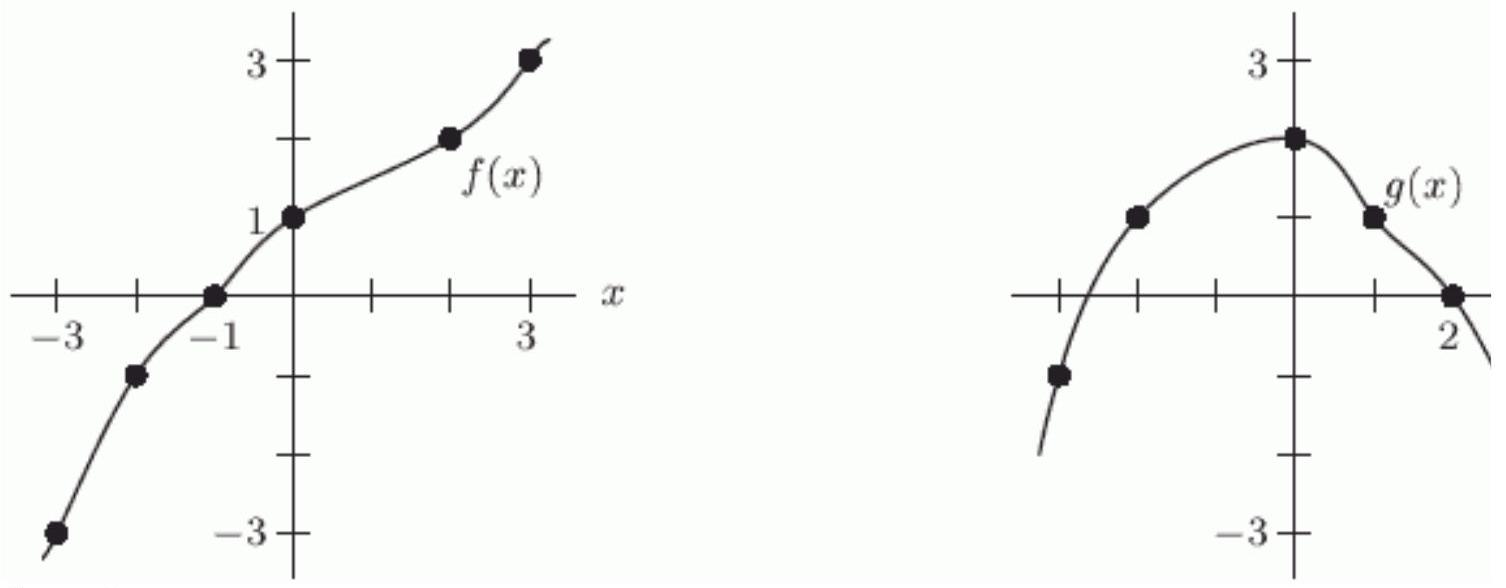

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
7
Let and . Using the table below gives -----------and -----------------
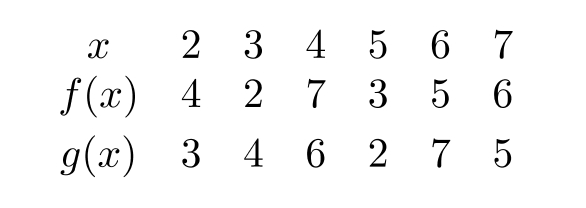
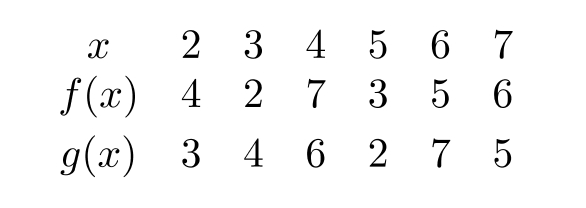

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
8
Given and , what is ?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
9
Let and . Does ?

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
10
If , which of the following could be true? Mark all that apply.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
11
If and , does ?

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
12
If and , what is ?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
13
Let and . What is ?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
14
Let and . What is ?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
15
Let be defined by the following graph.
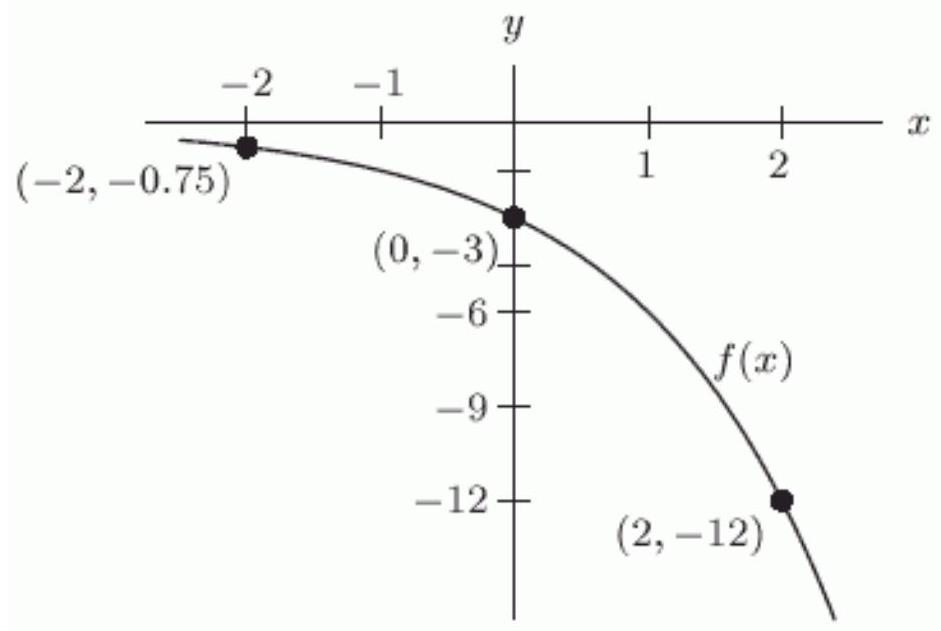
Describe the graph of .
A) A version of the graph of reflected across the -axis, stretched vertically by a factor of 2.
B) A version of the graph of reflected across the -axis, compressed by a factor of .
C) A version of the graph of reflected across the -axis, stretched vertically by a factor of 2.
D) A version of the graph of reflected across the -axis, compressed by a factor of 2..

Describe the graph of .
A) A version of the graph of reflected across the -axis, stretched vertically by a factor of 2.
B) A version of the graph of reflected across the -axis, compressed by a factor of .
C) A version of the graph of reflected across the -axis, stretched vertically by a factor of 2.
D) A version of the graph of reflected across the -axis, compressed by a factor of 2..

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
16
Let be defined by the following graph.
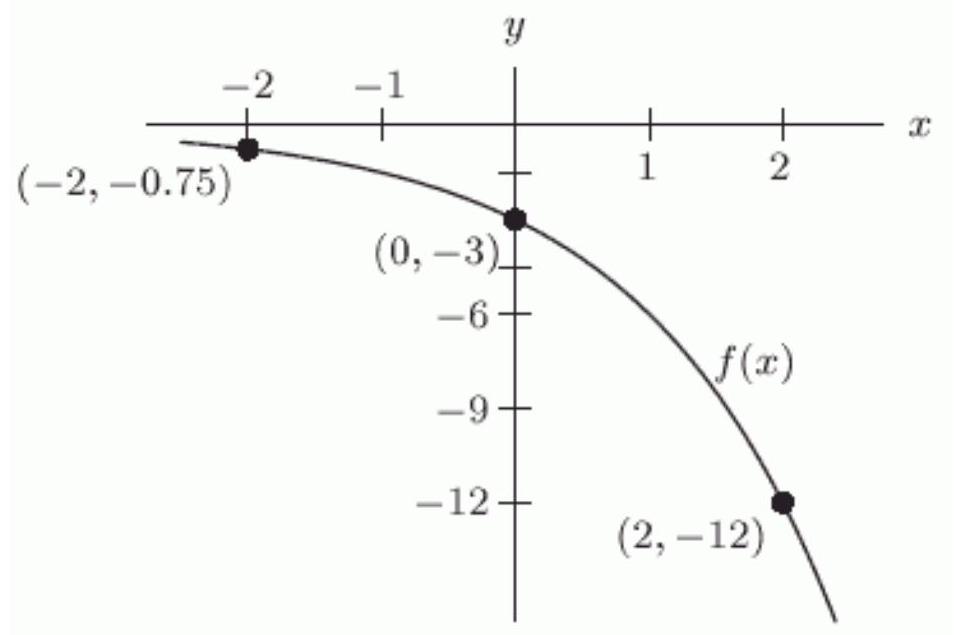
Describe the graph of .
A) A version of the graph of flipped about the -axis and shifted up by 2 units.
B) A version of the graph of flipped about the -axis and shifted down by 2 units.
C) A version of the graph of flipped about the -axis and shifted down by 2 units.
D) A version of the graph of flipped about the -axis and shifted up by 2 units.

Describe the graph of .
A) A version of the graph of flipped about the -axis and shifted up by 2 units.
B) A version of the graph of flipped about the -axis and shifted down by 2 units.
C) A version of the graph of flipped about the -axis and shifted down by 2 units.
D) A version of the graph of flipped about the -axis and shifted up by 2 units.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
17
Let . Does ?

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
18
Let , and . Does

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
19
Let and . Does ?

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
20
Let and . Does ?

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
21
Find for

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
22
If , which of the following could be true? Mark all that apply.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
23
A child building a tower with blocks places 18 blocks in the first row, 17 blocks in the second row, 16 blocks in the third row, and so forth. How many blocks are in the row?

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
24
Select the list of functions that is a decomposition of in the form of .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
25
Let . Does ?

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
26
Let and let . What is ?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
27
Given , what is ?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
28
Let and . Evaluate .

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
29
Let and . Evaluate to 2 decimal places.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
30
Given the graph of below, which of the following is a solution to the equation ?
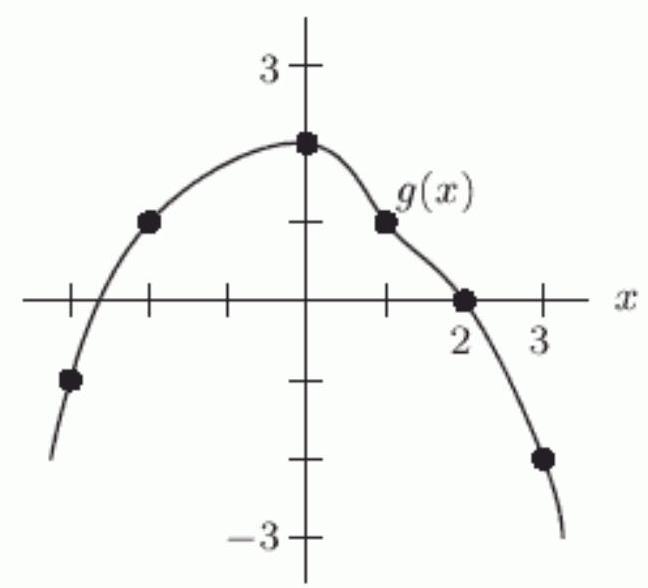
A) 1
B) 0
C) -3
D) 3
E) 2

A) 1
B) 0
C) -3
D) 3
E) 2

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
31
Given the graph of below, solve . If there is more than one answer, enter them from least to greatest, separated by semicolons. If there are no solutions, enter "none".
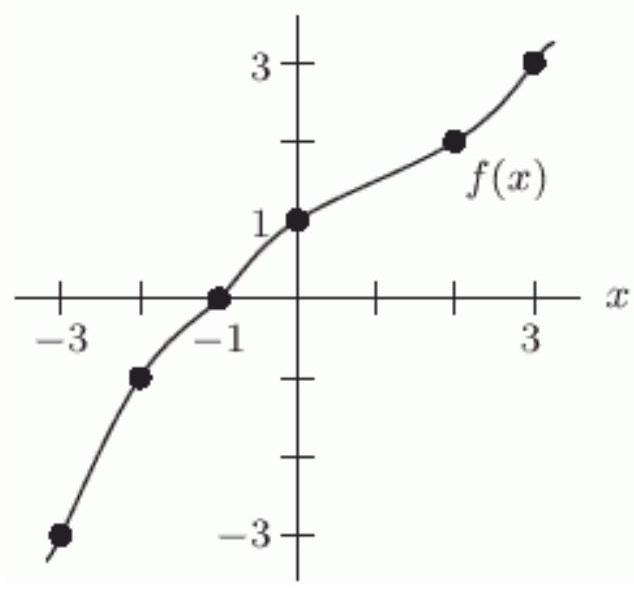


Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
32
Based on the following table, could the function be invertible?
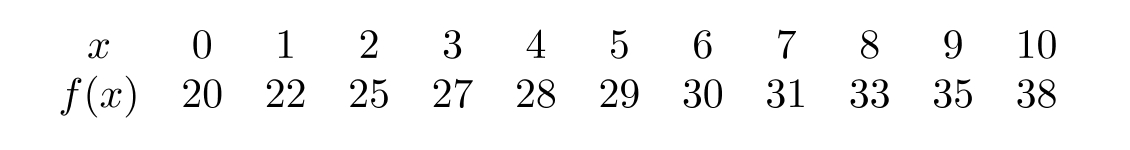
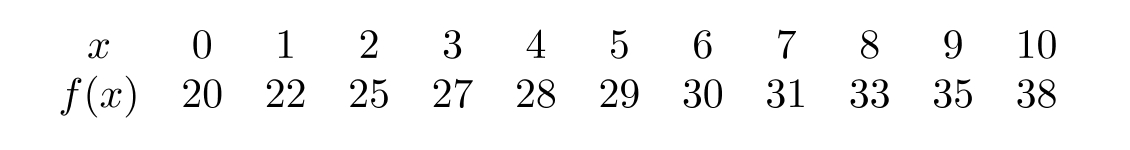

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
33
Is the function invertible if the domain of is all real numbers?

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
34
Is the function the inverse of the function ?

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
35
For positive numbers , what is the inverse of ?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
36
What is the inverse of ?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
37
Given , solve . Round to 3 decimal places.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
38
Given , solve .

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
39
Given , does ?

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
40
Let . Does ?

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
41
Is the function graphed below invertible?
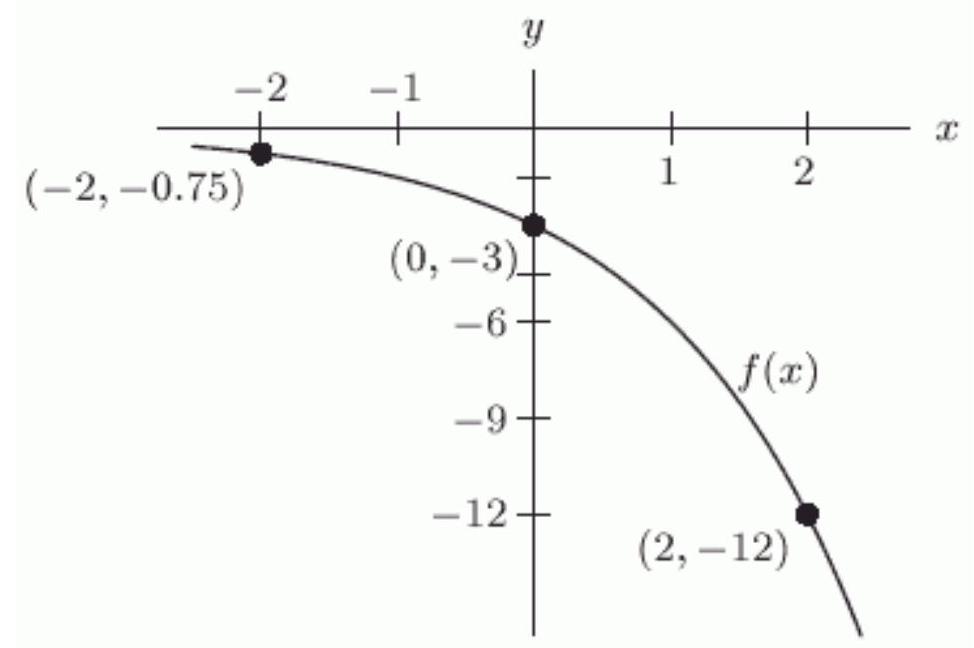


Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
42
Use a graph to determine whether or not is invertible.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
43
Let give the annual profit of a company (in thousands of dollars) years after its formation. What is ? Round to the nearest whole number and include units.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
44
The following figure defines a function .
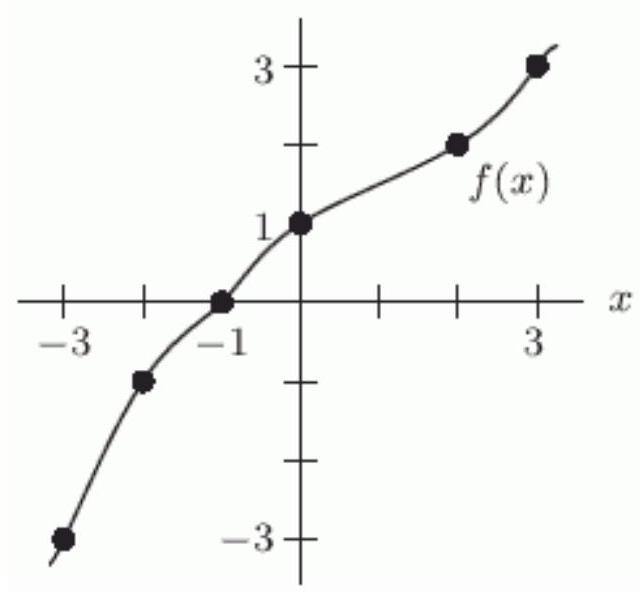
Which of the following quantities is greater?
A)
B)

Which of the following quantities is greater?
A)
B)

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
45
Suppose . What is the domain of ?
A) All real numbers greater than or equal to 8 .
B) All real numbers less than or equal to 8 .
C) All real numbers greater than or equal to 0 .
D) All real numbers less than or equal to 0 .
A) All real numbers greater than or equal to 8 .
B) All real numbers less than or equal to 8 .
C) All real numbers greater than or equal to 0 .
D) All real numbers less than or equal to 0 .

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
46
Let be a linear function with a positive slope and be a different linear function with a negative slope. Describe the graph of .
A) A pair of curves that approach both a horizontal and a vertical asymptote.
B) A parabola that opens upward.
C) Another linear function.
D) A parabola that opens downward.
A) A pair of curves that approach both a horizontal and a vertical asymptote.
B) A parabola that opens upward.
C) Another linear function.
D) A parabola that opens downward.

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
47
Let and for positive constants and . Let . If and , what is

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
48
Is the quotient of two even functions; odd, even, or neither?

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
49
For , does ?

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
50
The following table gives 3 functions, , and .
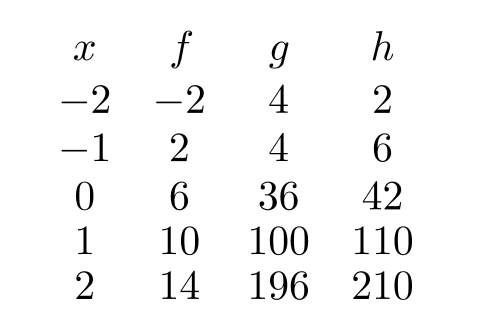
Which of the following statements is true?
A)
B)
C)
D)
E)
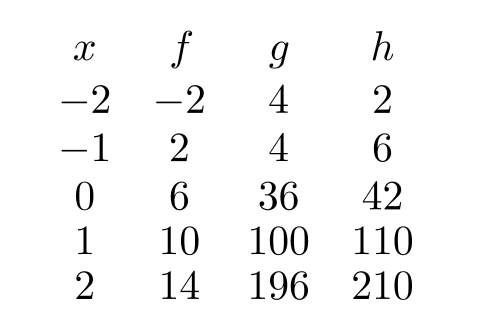
Which of the following statements is true?
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
51
The function is shown in the first figure.
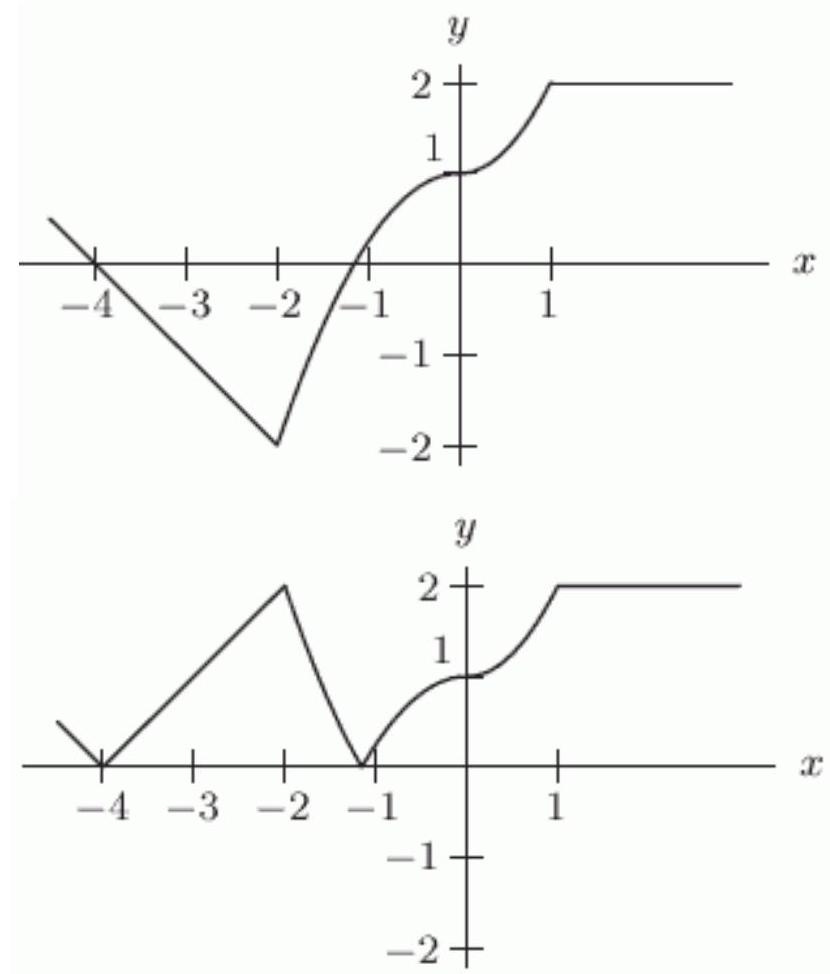
Which transformation of is shown in the second figure?
A)
B)
C)
D)

Which transformation of is shown in the second figure?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
52
The following table gives values for the functions , and , three functions defined only for the values . Based on the table, what is ?



Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
53
Let and . What is ?

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
54
The functions and are defined by the graph below. The dashed graph is and the solid graph is .
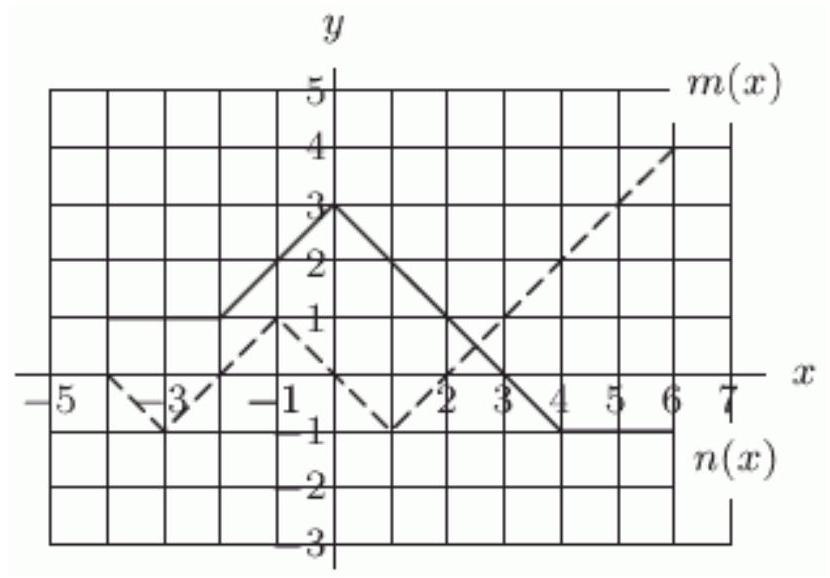
Evaluate .

Evaluate .

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
55
Let and . What is ?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
56
Let and . What is ?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
57
Let , and . What is ?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
58
Find if and .

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
59
Let and . Find a simplified formula for .

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
60
Let and . Find a simplified formula for the function .

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
61
Let be the number of men and be the number of women residing in a certain town in year . Let be the average income, in dollars, of residents of that town in year . If , and , find a simplified formula for the total amount of money earned by all adult residents of the town in year .

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
62
Let be the number of men and let be the number of women residing in a certain town in year . Let be the average income, in dollars, of residents of that town in year . If , and , find the total amount of money earned by all adult residents of the town in year 3 .

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
63
Find a simplified formula for given

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
64
Let . Find and simplify .

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
65
Find the function when and .

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
66
Find the function when and .

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
67
Find the function when and .

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
68
Find the function when and .

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck
69
Find the function when and .

Unlock Deck
Unlock for access to all 69 flashcards in this deck.
Unlock Deck
k this deck


