Exam 10: Compositions, Inverses, and Combinations of Functions
Exam 1: Linear Functions and Change148 Questions
Exam 2: Functions138 Questions
Exam 3: Quadratic Functions46 Questions
Exam 4: Exponential Functions94 Questions
Exam 5: Logarithmic Functions87 Questions
Exam 6: Transformations of Functions and Their Graphs85 Questions
Exam 7: Trigonometry and Periodic Functions178 Questions
Exam 8: Triangle Trigonometry and Polar Coordinates43 Questions
Exam 9: Trigonometric Identities, Models, and Complex Numbers106 Questions
Exam 10: Compositions, Inverses, and Combinations of Functions69 Questions
Exam 11: Polynomial and Rational Functions145 Questions
Exam 12: Vectors and Matrices104 Questions
Exam 13: Sequences and Series81 Questions
Exam 14: Parametric Equations and Conic Sections128 Questions
Select questions type
The following table gives 3 functions, , and .
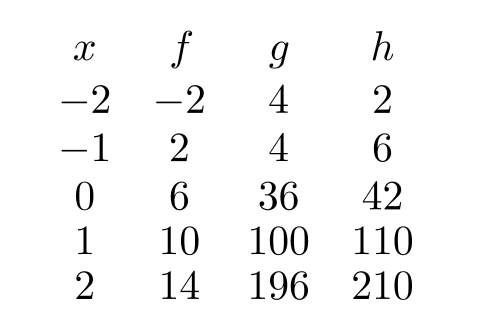 Which of the following statements is true?
Which of the following statements is true?
(Multiple Choice)
4.9/5  (33)
(33)
The following figure defines a function .
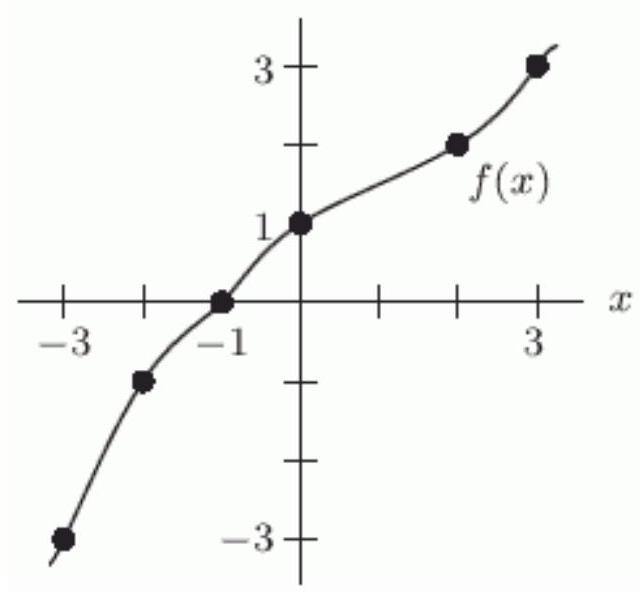 Which of the following quantities is greater?
Which of the following quantities is greater?
(Multiple Choice)
4.9/5  (32)
(32)
If , which of the following could be true? Mark all that apply.
(Multiple Choice)
4.7/5  (34)
(34)
Given the graph of below, solve . If there is more than one answer, enter them from least to greatest, separated by semicolons. If there are no solutions, enter "none".
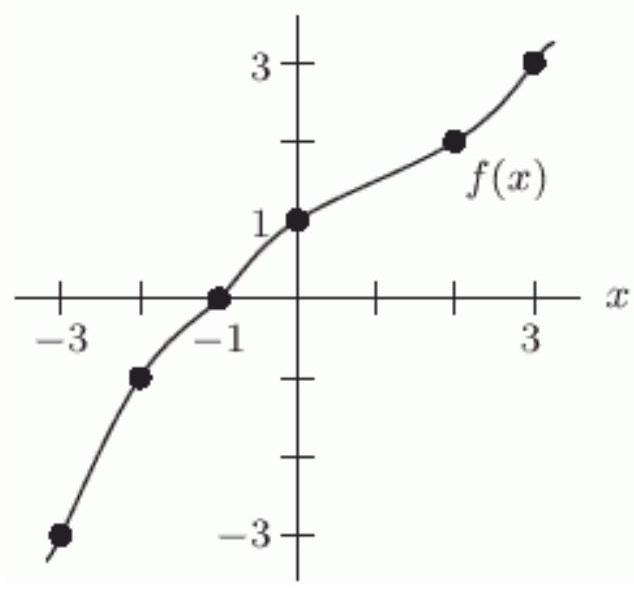
(Short Answer)
4.7/5  (31)
(31)
Let be the number of men and be the number of women residing in a certain town in year . Let be the average income, in dollars, of residents of that town in year . If , and , find a simplified formula for the total amount of money earned by all adult residents of the town in year .
(Short Answer)
4.9/5  (34)
(34)
The functions and are defined by the graph below. The dashed graph is and the solid graph is .
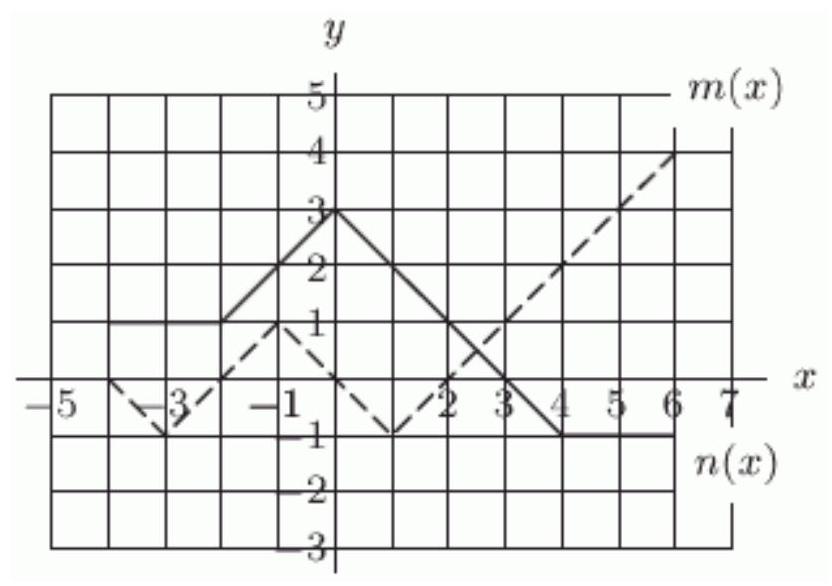 Evaluate .
Evaluate .
(Short Answer)
4.7/5  (36)
(36)
Let be a linear function with a positive slope and be a different linear function with a negative slope. Describe the graph of .
(Multiple Choice)
4.7/5  (31)
(31)
Showing 1 - 20 of 69
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)