Deck 1: Fundamentals
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/10
Play
Full screen (f)
Deck 1: Fundamentals
1
The instantaneous voltage across a circuit is volts, and the instantaneous current entering the positive terminal if the circuit element is A. For these circuit elements, calculate (a) the instantaneous power absorbed, (b) the real power (state whether it is delivered or absorbed), (c) the reactive power (state whether delivered or absorbed), (d) the power factor (state whether lagging or leading).
(a)
(b)
(c)
(b)
(c)
2
The voltage volts is applied to a load consisting of a resistor in parallel with a capacitive reactance . Calculate (a) the instantaneous power absorbed by the resistor, (b) the instantaneous power absorbed by the capacitor, (c) the real power absorbed by the resistor, (d) the reactive power delivered by the capacitor, (e) the load power factor.
(a)
(b)
(c) Absorbed
(d) VAR Delivered
(e)
(b)
(c) Absorbed
(d) VAR Delivered
(e)
3
if the resistor and capacitor are connected in series.
(a)
(b)
(c) Absorbed
(d) Delivered
(e) Leading
(b)
(c) Absorbed
(d) Delivered
(e) Leading
4
Consider a single-phase loadwith an applied voltage
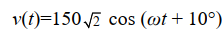 volts and load current
volts and load current 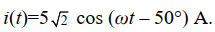
(a) Determinethe power triangle.
(b) Find the power factor and specify whether it islagging or leading.
(c) Calculate the reactive power supplied by capacitors in parallel with the load that correctthe power factor to 0.9 lagging.
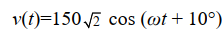 volts and load current
volts and load current 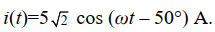
(a) Determinethe power triangle.
(b) Find the power factor and specify whether it islagging or leading.
(c) Calculate the reactive power supplied by capacitors in parallel with the load that correctthe power factor to 0.9 lagging.

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
5
A circuit consists of two impedances, and , in parallel, supplied by a source voltage volts. Determine the power triangle for each of the impedances and for the source.

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
6
An industrial plant consisting primarily of induction motor loads absorbs at 0.7 power factor lagging. (a) Compute the required kVA rating of a shunt capacitor to improve the power factor to 0.9 lagging. (b) Calculate the resulting power factor if a synchronous motor rated with efficiency operating at rated load and at unity power factor is added to the plant instead of the capacitor. Assume constant voltage.

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
7
The real power delivered by a source to two impedances, and , connected in parallel, is . Determine (a) the real power absorbed by each of the impedances and (b) the source current.

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
8
A single-phase source has a terminal voltage volts and a current , which leaves the positive terminal of the source. Determine the real and reactive power, and state whether the source is delivering or absorbing each.

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
9
A three-phase 25-kVA, 208-V, 60-Hz alternator, operating under balanced steady-state conditions, supplies a line current of 20 A per phase at a 0.8 lagging power factor and at rated voltage. Determine the power triangle for this operating condition.

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
10
Three identical impedances are connected in to a balanced threephase source by three identical line conductors with impedance per line. (a) Calculate the line-to-line voltage at the load terminals.
(b) Repeat part (a) when a -connected capacitor bank with reactance per phase is connected in parallel with the load.
(b) Repeat part (a) when a -connected capacitor bank with reactance per phase is connected in parallel with the load.

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck


