Exam 1: Fundamentals

An industrial plant consisting primarily of induction motor loads absorbs $1000 \mathrm{~kW}$ at 0.7 power factor lagging. (a) Compute the required kVA rating of a shunt capacitor to improve the power factor to 0.9 lagging. (b) Calculate the resulting power factor if a synchronous motor rated $1000 \mathrm{hp}$ with $90 \%$ efficiency operating at rated load and at unity power factor is added to the plant instead of the capacitor. Assume constant voltage. $(1 \mathrm{hp}=0.746 \mathrm{~kW})$

Free

(Essay)

4.7/5

(41)

Question 1

Correct Answer:

Verified

(a) $(a) \begin{aligned} \phi_{L} & =\cos ^{-1} 0.7=45.57^{\circ} \\ Q_{L} & =P \tan \phi_{L}=1000 \tan \left(43.57^{\circ}\right) \\ & =1020.2 \mathrm{kVAR} \\ \phi_{S} & =\cos ^{-1} 0.9=25.84^{\circ} \\ Q_{S} & =P \tan \phi_{S}=1000 \tan \left(25.84^{\circ}\right)=484.3 \mathrm{kVAR} \\ Q_{C} & =Q_{L}-Q_{S}=1020.2-484.3=535.9 \mathrm{kVAR} \\ S_{C} & =Q_{C}=535.9 \mathrm{kVA} \end{aligned} (b) Synchronous motor absorbs P_{m}=\frac{1000 \times 0.746}{0.9}=828.9 \mathrm{~kW} and Q_{m}=0 \mathrm{kVAR} \begin{aligned} \text { Source } p f & =\cos \left[\tan ^{-1} \frac{1020.2}{1828.9}\right] \\ & =0.873 \text { Lagging } \end{aligned}$
$\begin{aligned}\phi_{L} & =\cos ^{-1} 0.7=45.57^{\circ} \\Q_{L} & =P \tan \phi_{L}=1000 \tan \left(43.57^{\circ}\right) \\& =1020.2 \mathrm{kVAR} \\\phi_{S} & =\cos ^{-1} 0.9=25.84^{\circ} \\Q_{S} & =P \tan \phi_{S}=1000 \tan \left(25.84^{\circ}\right)=484.3 \mathrm{kVAR} \\Q_{C} & =Q_{L}-Q_{S}=1020.2-484.3=535.9 \mathrm{kVAR} \\S_{C} & =Q_{C}=535.9 \mathrm{kVA}\end{aligned}$
(b) Synchronous motor absorbs $P_{m}=\frac{1000 \times 0.746}{0.9}=828.9 \mathrm{~kW}$ and $Q_{m}=0 \mathrm{kVAR}$
$\begin{aligned}\text { Source } p f & =\cos \left[\tan ^{-1} \frac{1020.2}{1828.9}\right] \\& =0.873 \text { Lagging }\end{aligned}$
$(a) \begin{aligned} \phi_{L} & =\cos ^{-1} 0.7=45.57^{\circ} \\ Q_{L} & =P \tan \phi_{L}=1000 \tan \left(43.57^{\circ}\right) \\ & =1020.2 \mathrm{kVAR} \\ \phi_{S} & =\cos ^{-1} 0.9=25.84^{\circ} \\ Q_{S} & =P \tan \phi_{S}=1000 \tan \left(25.84^{\circ}\right)=484.3 \mathrm{kVAR} \\ Q_{C} & =Q_{L}-Q_{S}=1020.2-484.3=535.9 \mathrm{kVAR} \\ S_{C} & =Q_{C}=535.9 \mathrm{kVA} \end{aligned} (b) Synchronous motor absorbs P_{m}=\frac{1000 \times 0.746}{0.9}=828.9 \mathrm{~kW} and Q_{m}=0 \mathrm{kVAR} \begin{aligned} \text { Source } p f & =\cos \left[\tan ^{-1} \frac{1020.2}{1828.9}\right] \\ & =0.873 \text { Lagging } \end{aligned}$

Consider a single-phase loadwith an applied voltage 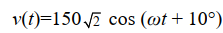volts and load current 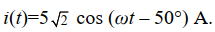(a) Determinethe power triangle. (b) Find the power factor and specify whether it islagging or leading. (c) Calculate the reactive power supplied by capacitors in parallel with the load that correctthe power factor to 0.9 lagging.

Free

(Essay)

4.7/5

(30)

Question 2

Correct Answer:

Verified

a. 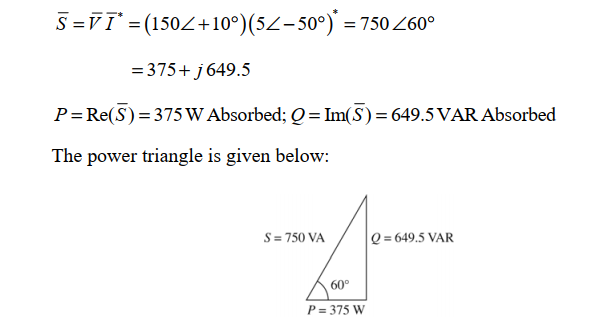b.pf=cos 60°=0.5 Lagging
c.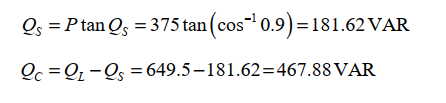

Three identical impedances $Z_{\Delta}=20 / 60^{\circ} \Omega$ are connected in $\Delta$ to a balanced threephase $480-\mathrm{V}$ source by three identical line conductors with impedance $Z_{\mathrm{L}}=$ $(0.8+j 0.6) \Omega$ per line. (a) Calculate the line-to-line voltage at the load terminals. (b) Repeat part (a) when a $\Delta$ -connected capacitor bank with reactance $(-j 20) \Omega$ per phase is connected in parallel with the load.

Free

(Essay)

4.8/5

(44)

Question 3

Correct Answer:

Verified

(a)
$(a) Using voltage division: \bar{V}_{A N}=\bar{V}_{a n} \frac{\bar{Z}_{\Delta} / 3}{\left(Z_{\Delta} / 3\right)+\bar{Z}_{L I N E}} \bar{V}_{A N}=\frac{208}{\sqrt{3}} \frac{6.667 \angle 60^{\circ}}{6.667 \angle 60^{\circ}+(0.8+j 0.6)}=105.4 \angle 2.96^{\circ} \mathrm{V} Load voltage V_{A B}=\sqrt{3} 105.4=182.6 \mathrm{~V}(\mathrm{~L}-\mathrm{L}) (b) \begin{aligned} & \bar{V}_{A N}=\bar{V}_{a n} \frac{\bar{Ƶ}_{e q}}{\bar{Ƶ}_{e q}+\bar{Ƶ}_{L I N E}} ; \bar{Ƶ}_{e q}=\left(6.667 \angle 60^{\circ}\right) \|(-j 6.667) \\ & =12.88 \angle-15^{\circ} \Omega \\ & \bar{V}_{A N}=\left(\frac{208}{\sqrt{3}} \angle 0^{\circ}\right)\left[\frac{12.88 \angle-15^{\circ}}{\left(12.88 \angle-15^{\circ}\right)+0.8+j 0.6}\right]=114.4 \angle-3.35^{\circ} \mathrm{V} \end{aligned} The load line to line voltage is V_{A B}=\sqrt{3} 114.4=198.1 \mathrm{~V}$
Using voltage division: $\bar{V}_{A N}=\bar{V}_{a n} \frac{\bar{Z}_{\Delta} / 3}{\left(Z_{\Delta} / 3\right)+\bar{Z}_{L I N E}}$
$\bar{V}_{A N}=\frac{208}{\sqrt{3}} \frac{6.667 \angle 60^{\circ}}{6.667 \angle 60^{\circ}+(0.8+j 0.6)}=105.4 \angle 2.96^{\circ} \mathrm{V}$
Load voltage $V_{A B}=\sqrt{3} 105.4=182.6 \mathrm{~V}(\mathrm{~L}-\mathrm{L})$
(b)
$(a) Using voltage division: \bar{V}_{A N}=\bar{V}_{a n} \frac{\bar{Z}_{\Delta} / 3}{\left(Z_{\Delta} / 3\right)+\bar{Z}_{L I N E}} \bar{V}_{A N}=\frac{208}{\sqrt{3}} \frac{6.667 \angle 60^{\circ}}{6.667 \angle 60^{\circ}+(0.8+j 0.6)}=105.4 \angle 2.96^{\circ} \mathrm{V} Load voltage V_{A B}=\sqrt{3} 105.4=182.6 \mathrm{~V}(\mathrm{~L}-\mathrm{L}) (b) \begin{aligned} & \bar{V}_{A N}=\bar{V}_{a n} \frac{\bar{Ƶ}_{e q}}{\bar{Ƶ}_{e q}+\bar{Ƶ}_{L I N E}} ; \bar{Ƶ}_{e q}=\left(6.667 \angle 60^{\circ}\right) \|(-j 6.667) \\ & =12.88 \angle-15^{\circ} \Omega \\ & \bar{V}_{A N}=\left(\frac{208}{\sqrt{3}} \angle 0^{\circ}\right)\left[\frac{12.88 \angle-15^{\circ}}{\left(12.88 \angle-15^{\circ}\right)+0.8+j 0.6}\right]=114.4 \angle-3.35^{\circ} \mathrm{V} \end{aligned} The load line to line voltage is V_{A B}=\sqrt{3} 114.4=198.1 \mathrm{~V}$
$\begin{aligned}& \bar{V}_{A N}=\bar{V}_{a n} \frac{\bar{Ƶ}_{e q}}{\bar{Ƶ}_{e q}+\bar{Ƶ}_{L I N E}} ; \bar{Ƶ}_{e q}=\left(6.667 \angle 60^{\circ}\right) \|(-j 6.667) \\& =12.88 \angle-15^{\circ} \Omega \\& \bar{V}_{A N}=\left(\frac{208}{\sqrt{3}} \angle 0^{\circ}\right)\left[\frac{12.88 \angle-15^{\circ}}{\left(12.88 \angle-15^{\circ}\right)+0.8+j 0.6}\right]=114.4 \angle-3.35^{\circ} \mathrm{V}\end{aligned}$
The load line to line voltage is $V_{A B}=\sqrt{3} 114.4=198.1 \mathrm{~V}$

The real power delivered by a source to two impedances, $\mathrm{Z}_{1}$ $=3+j 5 \mathrm{~W}$ and $\mathrm{Z}_{2}=10 \mathrm{~W}$ , connected in parallel, is $2000 \mathrm{~W}$ . Determine (a) the real power absorbed by each of the impedances and (b) the source current.

(Essay)

4.7/5

(37)

Question 4

The instantaneous voltage across a circuit is $v(t)=678.8 \sin$ $\left(\omega t-15^{\circ}\right)$ volts, and the instantaneous current entering the positive terminal if the circuit element is $i(t)=200 \cos \left(\omega t-5^{\circ}\right)$ A. For these circuit elements, calculate (a) the instantaneous power absorbed, (b) the real power (state whether it is delivered or absorbed), (c) the reactive power (state whether delivered or absorbed), (d) the power factor (state whether lagging or leading).

(Essay)

4.7/5

(37)

Question 5

if the resistor and capacitor are connected in series.

(Essay)

4.9/5

(30)

Question 6

A three-phase 25-kVA, 208-V, 60-Hz alternator, operating under balanced steady-state conditions, supplies a line current of 20 A per phase at a 0.8 lagging power factor and at rated voltage. Determine the power triangle for this operating condition.

(Essay)

4.9/5

(38)

Question 7

A circuit consists of two impedances, $Z_{1}=20 \angle 30^{\circ} \Omega$ and $Z_{2}=14.14 \angle-45^{\circ} \Omega$ , in parallel, supplied by a source voltage $V=100 \angle 60^{\circ}$ volts. Determine the power triangle for each of the impedances and for the source.

(Essay)

4.8/5

(47)

Question 8

The voltage $v(t)=678.8 \cos \left(\omega t+45^{\circ}\right)$ volts is applied to a load consisting of a $10-\mathrm{W}$ resistor in parallel with a capacitive reactance $\mathrm{X}_{\mathrm{C}}=25 \mathrm{~W}$ . Calculate (a) the instantaneous power absorbed by the resistor, (b) the instantaneous power absorbed by the capacitor, (c) the real power absorbed by the resistor, (d) the reactive power delivered by the capacitor, (e) the load power factor.

(Essay)

4.8/5

(31)

Question 9

A single-phase source has a terminal voltage $V=120 \angle 0^{\circ}$ volts and a current $I=25 \angle 30^{\circ} \mathrm{A}$ , which leaves the positive terminal of the source. Determine the real and reactive power, and state whether the source is delivering or absorbing each.

(Essay)

4.9/5

(40)

Question 10

Showing 1 - 10 of 10

The real power delivered by a source to two impedances, $\mathrm{Z}_{1}$ $=3+j 5 \mathrm{~W}$ and $\mathrm{Z}_{2}=10 \mathrm{~W}$ , connected in parallel, is $2000 \mathrm{~W}$ . Determine (a) the real power absorbed by each of the impedances and (b) the source current.

if the resistor and capacitor are connected in series.

A three-phase 25-kVA, 208-V, 60-Hz alternator, operating under balanced steady-state conditions, supplies a line current of 20 A per phase at a 0.8 lagging power factor and at rated voltage. Determine the power triangle for this operating condition.

A circuit consists of two impedances, $Z_{1}=20 \angle 30^{\circ} \Omega$ and $Z_{2}=14.14 \angle-45^{\circ} \Omega$ , in parallel, supplied by a source voltage $V=100 \angle 60^{\circ}$ volts. Determine the power triangle for each of the impedances and for the source.

A single-phase source has a terminal voltage $V=120 \angle 0^{\circ}$ volts and a current $I=25 \angle 30^{\circ} \mathrm{A}$ , which leaves the positive terminal of the source. Determine the real and reactive power, and state whether the source is delivering or absorbing each.

Power Transformers

Transmission Line Parameters

Transmission Lines: Steady-State Operation

Power Flows

Symmetrical Faults

Symmetrical Components

Filters