Deck 11: Monte Carlo Simulation
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/59
Play
Full screen (f)
Deck 11: Monte Carlo Simulation
1
Reference - 11.1: Use the graph given below to answer questions 14-15.
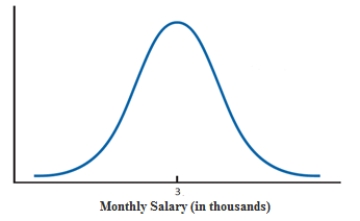
Reference - 11.1: The type of distribution shown in the graph is
A) uniform.
B) normal.
C) exponential.
D) beta.

Reference - 11.1: The type of distribution shown in the graph is
A) uniform.
B) normal.
C) exponential.
D) beta.
normal.
2
In a base-case scenario, the output is determined by assuming
A) worst values that can be expected for the random variables of a model.
B) the mean trial values for the random variables of a model.
C) best values that can be expected for the random variables of a model.
D) the most likely values for the random variables of a model.
A) worst values that can be expected for the random variables of a model.
B) the mean trial values for the random variables of a model.
C) best values that can be expected for the random variables of a model.
D) the most likely values for the random variables of a model.
the most likely values for the random variables of a model.
3
In simulation analysis, the _____ of random variables can be adjusted to determine the impact of the assumptions about the shape of the uncertainty on the results.
A) probability distributions
B) ranges
C) relative frequencies
D) manual generations
A) probability distributions
B) ranges
C) relative frequencies
D) manual generations
probability distributions
4
A distribution of a random variable for which values extremely larger or smaller than the mean are increasingly unlikely can possibly be modeled as a(n) _____ probability distribution.
A) binomial
B) normal
C) exponential
D) gamma
A) binomial
B) normal
C) exponential
D) gamma

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
5
A disadvantage of the simple what-if analyses is that
A) there are errors induced as a result of rounding.
B) the optimal solutions are not guaranteed.
C) there is no indication of the likelihood of various output values.
D) it cannot compute alternate optimal solutions.
A) there are errors induced as a result of rounding.
B) the optimal solutions are not guaranteed.
C) there is no indication of the likelihood of various output values.
D) it cannot compute alternate optimal solutions.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
6
Which of the following inferences about a variable of interest can be drawn from the graph given below? 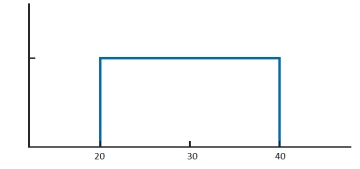
A) The variable is equally likely to take any value between 20 and 40.
B) The variable is more likely to take the value 20 than 40.
C) The variable is more likely to take any value outside the range of 20 and 40.
D) The variable can only take the value 30.

A) The variable is equally likely to take any value between 20 and 40.
B) The variable is more likely to take the value 20 than 40.
C) The variable is more likely to take any value outside the range of 20 and 40.
D) The variable can only take the value 30.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
7
The values for random variables in a Monte Carlo simulation are
A) selected manually.
B) generated randomly from probability distributions.
C) taken from forecasting analysis.
D) derived secondarily using formulas.
A) selected manually.
B) generated randomly from probability distributions.
C) taken from forecasting analysis.
D) derived secondarily using formulas.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
8
Reference - 11.1: Use the graph given below to answer questions 14-15.

Reference - 11.1: Which of the following inferences can be drawn about the monthly salary?
A) The average monthly salary is $3000.
B) The monthly salary is always less than $3000.
C) The monthly salary is always greater than $3000.
D) The range of the monthly salary distribution is $3000 to $5000.

Reference - 11.1: Which of the following inferences can be drawn about the monthly salary?
A) The average monthly salary is $3000.
B) The monthly salary is always less than $3000.
C) The monthly salary is always greater than $3000.
D) The range of the monthly salary distribution is $3000 to $5000.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
9
An input to a simulation model that is selected by the decision maker is known as a _____.
A) random variable
B) nonnegativity constraint
C) probable input
D) controllable input
A) random variable
B) nonnegativity constraint
C) probable input
D) controllable input

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
10
A _____ uses repeated random sampling to represent uncertainty in a model representing a real system and that computes the values of model outputs.
A) Monte Carlo simulation
B) what-if analysis
C) deterministic model
D) discrete event simulation
A) Monte Carlo simulation
B) what-if analysis
C) deterministic model
D) discrete event simulation

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
11
A simulation model extends spreadsheet modeling by
A) extending the range of parameters for which solutions are computed.
B) using real-time values for parameters from the application to formulate solutions.
C) replacing the use of single values for parameters with a range of possible values.
D) using historical data to make predictions about future values and expected trends.
A) extending the range of parameters for which solutions are computed.
B) using real-time values for parameters from the application to formulate solutions.
C) replacing the use of single values for parameters with a range of possible values.
D) using historical data to make predictions about future values and expected trends.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
12
A(n) _____ is an input to a simulation model whose value is uncertain and described by a probability distribution.
A) identifier
B) constraint
C) random variable
D) decision variable
A) identifier
B) constraint
C) random variable
D) decision variable

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
13
A _____ analysis involves considering alternative values for the random variables and computing the resulting value for the output.
A) random
B) what-if
C) risk
D) cluster
A) random
B) what-if
C) risk
D) cluster

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
14
The outcome of a simulation experiment is a(n)
A) objective function.
B) probability distribution for one or more output measures.
C) single number.
D) what-if scenario.
A) objective function.
B) probability distribution for one or more output measures.
C) single number.
D) what-if scenario.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
15
A description of the range and relative likelihood of possible values of an uncertain variable is known as a _____.
A) risk analysis
B) probability distribution
C) base-case scenario
D) simulation optimization
A) risk analysis
B) probability distribution
C) base-case scenario
D) simulation optimization

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
16
A set of values for the random variables is called a(n) _____.
A) event
B) permutation
C) trial
D) combination
A) event
B) permutation
C) trial
D) combination

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
17
The choice of the probability distribution for a random variable can be guided by
A) an objective function.
B) likelihood factors.
C) forecasting.
D) historical data.
A) an objective function.
B) likelihood factors.
C) forecasting.
D) historical data.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
18
The process of evaluating a decision in the face of uncertainty by quantifying the likelihood and magnitude of an undesirable outcome is known as _____.
A) risk analysis
B) regression analysis
C) data mining
D) decision tree analysis
A) risk analysis
B) regression analysis
C) data mining
D) decision tree analysis

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
19
In a _____, a random variable can take any value in a specified range.
A) discrete probability distribution
B) cumulative distribution
C) relative frequency distribution
D) continuous probability distribution
A) discrete probability distribution
B) cumulative distribution
C) relative frequency distribution
D) continuous probability distribution

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
20
The range of computer-generated random numbers is _____.
A) [-∞, ∞]
B) [-∞, 0)
C) [1, ∞]
D) [0, 1)
A) [-∞, ∞]
B) [-∞, 0)
C) [1, ∞]
D) [0, 1)

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
21
The process of determining that a computer program implements a simulation model as it is intended is known as _____.
A) validation
B) verification
C) correlation
D) optimization
A) validation
B) verification
C) correlation
D) optimization

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
22
_____ is the process of determining that a simulation model provides an accurate representation of a real system.
A) Regression
B) Verification
C) Consideration
D) Validation
A) Regression
B) Verification
C) Consideration
D) Validation

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
23
The weekly demand for an item in a retail store follows a uniform distribution over the range 70 to 83. What would be the weekly demand if its corresponding computer-generated value is 0.5?
A) 90.1
B) 83
C) 76.5
D) 50.85
A) 90.1
B) 83
C) 76.5
D) 50.85

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
24
For a given mean and standard deviation, the _____ function in Excel is used to generate a value for the random variable characterized by a normal distribution.
A) NORM.INV
B) RAND
C) VLOOKUP
D) FREQUENCY
A) NORM.INV
B) RAND
C) VLOOKUP
D) FREQUENCY

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
25
The Excel function _____ generates integer values between lower and upper bounds.
A) RAND
B) RANDBETWEEN
C) LOWER
D) UPPER
A) RAND
B) RANDBETWEEN
C) LOWER
D) UPPER

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
26
ASP cannot guarantee an optimal solution to a simulation optimization model because
A) the optimization problem will have only one local optimal solution due to the linear relationship.
B) of sampling error resulting from nonlinear relationships.
C) it is not possible to compare solutions across runs.
D) of sampling error resulting from the presence of the random variables.
A) the optimization problem will have only one local optimal solution due to the linear relationship.
B) of sampling error resulting from nonlinear relationships.
C) it is not possible to compare solutions across runs.
D) of sampling error resulting from the presence of the random variables.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
27
In a simulation process, the error of the estimates of the output can be reduced by
A) increasing the range of possible values for the random variables.
B) increasing the number of random variables.
C) increasing the number of trials per simulation.
D) conducting regression analysis to forecast values.
A) increasing the range of possible values for the random variables.
B) increasing the number of random variables.
C) increasing the number of trials per simulation.
D) conducting regression analysis to forecast values.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
28
In Excel, the expression LN(RAND())*(-m) would generate a(n) _____ random variable with mean m.
A) lognormal
B) logarithmic
C) normal
D) exponential
A) lognormal
B) logarithmic
C) normal
D) exponential

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
29
Which of the following is true of verification?
A) It is largely a debugging task.
B) It requires an agreement among analysts and managers.
C) It deals with the accurate modeling of real system operations.
D) It is performed prior to the development of the computer procedure for simulation.
A) It is largely a debugging task.
B) It requires an agreement among analysts and managers.
C) It deals with the accurate modeling of real system operations.
D) It is performed prior to the development of the computer procedure for simulation.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
30
In a(n) _____ relationship between two quantities, either one quantity never increases as the other increases, or one quantity never decreases as the other increases.
A) monotonic
B) random
C) classified
D) independent
A) monotonic
B) random
C) classified
D) independent

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
31
Which of the following parameters is required to convert a computer-generated random variable into a uniform random variable?
A) Range of the distribution
B) Mean of the distribution
C) Variance of the distribution
D) Moments of the distribution
A) Range of the distribution
B) Mean of the distribution
C) Variance of the distribution
D) Moments of the distribution

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
32
The Excel add-in _____ is used to design a spreadsheet simulation model.
A) Analytic Solver Platform
B) Goal Seek
C) Solver
D) GPSS
A) Analytic Solver Platform
B) Goal Seek
C) Solver
D) GPSS

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
33
_____ is a measure of dependence between two random variables.
A) Approximation
B) Verification
C) Correlation
D) Validation
A) Approximation
B) Verification
C) Correlation
D) Validation

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
34
Which of the following is a disadvantage of using simulation?
A) Experimenting directly with a simulation model is often not feasible.
B) Each simulation run provides only a sample of how the real system will operate.
C) The simulation models are used to describe systems without requiring the assumptions that are required by mathematical models.
D) Simulation models warn against poor decision strategies by projecting disastrous outcomes such as system failures, large financial losses, and so on.
A) Experimenting directly with a simulation model is often not feasible.
B) Each simulation run provides only a sample of how the real system will operate.
C) The simulation models are used to describe systems without requiring the assumptions that are required by mathematical models.
D) Simulation models warn against poor decision strategies by projecting disastrous outcomes such as system failures, large financial losses, and so on.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
35
According to the _____, the sum of independent random variables can be approximated by a normal probability distribution.
A) what-if analysis
B) central limit theorem
C) simulation optimization approach
D) discrete-event simulation method
A) what-if analysis
B) central limit theorem
C) simulation optimization approach
D) discrete-event simulation method

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
36
Which of the following is true of simulation optimization using Analytic Solver Platform (ASP)?
A) It is computationally simple and cheap.
B) It can be executed in a very short time.
C) It is an iterative process.
D) It guarantees an optimal solution.
A) It is computationally simple and cheap.
B) It can be executed in a very short time.
C) It is an iterative process.
D) It guarantees an optimal solution.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
37
The _____ function is used to generate a pseudorandom number in Excel.
A) FREQUENCY()
B) RAND()
C) NORM.INV()
D) ROUND()
A) FREQUENCY()
B) RAND()
C) NORM.INV()
D) ROUND()

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
38
All the values of computer-generated random numbers are_____.
A) Poisson distributed
B) lognormally distributed
C) uniformly distributed
D) normally distributed
A) Poisson distributed
B) lognormally distributed
C) uniformly distributed
D) normally distributed

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
39
The random variables corresponding to the interarrival times of customers and the service times of customers are commonly described by a(n) _____ distribution.
A) Poisson
B) Rayleigh
C) lognormal
D) exponential
A) Poisson
B) Rayleigh
C) lognormal
D) exponential

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
40
The _____ function in Excel is used to compute the statistics required to create a histogram.
A) NORM.INV
B) RAND
C) FREQUENCY
D) STDEV.S
A) NORM.INV
B) RAND
C) FREQUENCY
D) STDEV.S

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
41
The manager of a company decides to arrange a party for being promoted and has invited 50 guests for dinner. The following table contains information on the number of RSVP'ed guests. He assumes that 12 people will not turn up. He also estimates that 13 guests planning to come solo has a 65 percent chance of attending alone, a 30 percent chance of not attending, and a 5 percent chance of bringing a companion. For each of the 20 guests who plan to bring a companion, there is a 75 percent chance that she or he will attend with a companion, a 10 percent chance of attending solo, and a 15 percent chance of not attending at all. For the 5 people who have not responded, the wedding planner assumes that there is an 85 percent chance that each will not attend, a 10 percent chance they will attend alone, and a 5 percent chance they will attend with a companion.
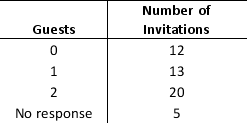 a. Assist the manager by constructing a spreadsheet simulation model to determine the expected number of guests who will attend the party.
a. Assist the manager by constructing a spreadsheet simulation model to determine the expected number of guests who will attend the party.
b. Use the Monte Carlo simulation model to determine X, the minimum number of guests for whom the dinner needs to be ordered, so that there is at least a 95 percent chance that the actual attendance is less than or equal to X. What is the best estimate for the value of X?
 a. Assist the manager by constructing a spreadsheet simulation model to determine the expected number of guests who will attend the party.
a. Assist the manager by constructing a spreadsheet simulation model to determine the expected number of guests who will attend the party.b. Use the Monte Carlo simulation model to determine X, the minimum number of guests for whom the dinner needs to be ordered, so that there is at least a 95 percent chance that the actual attendance is less than or equal to X. What is the best estimate for the value of X?

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
42
Consider the table below with information regarding each activity, immediate predecessors, and duration estimates (in minutes) for each activity.
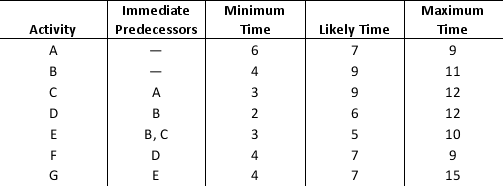
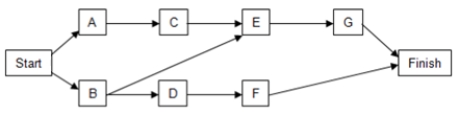 a. Using the PERT distribution in ASP to represent the duration of each activity, construct a simulation model to compute the total time to complete the task.
a. Using the PERT distribution in ASP to represent the duration of each activity, construct a simulation model to compute the total time to complete the task.
b. What is the expected duration of the entire project? What is the standard deviation of the project duration?
c. What is the likelihood that the project will be complete in 26 minutes?

 a. Using the PERT distribution in ASP to represent the duration of each activity, construct a simulation model to compute the total time to complete the task.
a. Using the PERT distribution in ASP to represent the duration of each activity, construct a simulation model to compute the total time to complete the task.b. What is the expected duration of the entire project? What is the standard deviation of the project duration?
c. What is the likelihood that the project will be complete in 26 minutes?

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
43
A branded store has outlets around the world that generates profit in the British pound, the New Zealand kiwi, and the Japanese yen. At the end of each quarter, the store converts the revenue from these three international outlets back into U.S. dollars, exposing itself to exchange rate risk. The current exchange rates are US$1.56 per £1, US$0.85 per NZD$1, and US$0.02 per ¥1. The management of the store wants to construct a simulation model to assess its vulnerability to uncertain exchange rate fluctuations. The quarterly profits earned in British pounds, New Zealand kiwis, and Japanese yen are £150,000, NZD$200,000, and ¥9,000,000, respectively. The data is given below.
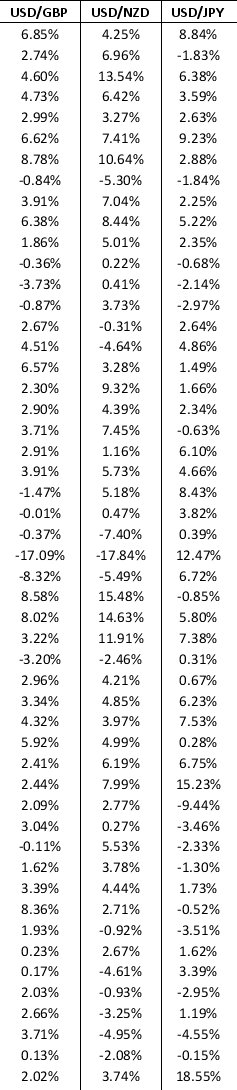 a. If exchange rates stay at their current values, what is the total quarterly profit in U.S. dollars?
a. If exchange rates stay at their current values, what is the total quarterly profit in U.S. dollars?
b. Model the uncertainty in the quarterly changes of the exchange rates between U.S. dollars and British pounds, New Zealand kiwis, and Japanese yen using a SLURP. Use your simulation model to estimate the average total quarterly profit in U.S. dollars. What is the probability that the total quarterly profit will be lower than the answer in part a?
 a. If exchange rates stay at their current values, what is the total quarterly profit in U.S. dollars?
a. If exchange rates stay at their current values, what is the total quarterly profit in U.S. dollars?b. Model the uncertainty in the quarterly changes of the exchange rates between U.S. dollars and British pounds, New Zealand kiwis, and Japanese yen using a SLURP. Use your simulation model to estimate the average total quarterly profit in U.S. dollars. What is the probability that the total quarterly profit will be lower than the answer in part a?

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
44
A specialty hedge fund is considering the purchase of a Jackson Pollock painting. It estimates the value of the painting to be $185 million. In an auction, both the number of competing bids and the amount of the competing bids is uncertain. The hedge fund has maintained a file summarizing 10 recent art auctions that it believes are similar to the upcoming auction. It is considering a bid of $163 million and would like to evaluate its chances of winning the upcoming auction with this bid.
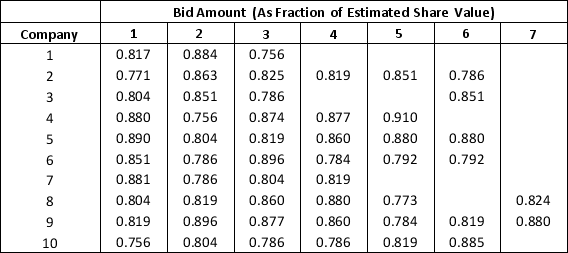 a. Construct a spreadsheet simulation model for this auction. Use a discrete uniform distribution between the minimum and maximum number of bidders in the 10 observed auctions to model the number of bidders in the Jackson Pollock auction. Fit a realistic distribution to the bid data to generate values of competing bid amounts. Use ASP to apply simulation optimization to determine the hedge fund's bid amount that maximizes the expected return = P(winning auction)*(185 - bid amount). Hint: Placing reasonable bounds on the highest and lowest possible bid amount will greatly assist the optimization algorithm.
a. Construct a spreadsheet simulation model for this auction. Use a discrete uniform distribution between the minimum and maximum number of bidders in the 10 observed auctions to model the number of bidders in the Jackson Pollock auction. Fit a realistic distribution to the bid data to generate values of competing bid amounts. Use ASP to apply simulation optimization to determine the hedge fund's bid amount that maximizes the expected return = P(winning auction)*(185 - bid amount). Hint: Placing reasonable bounds on the highest and lowest possible bid amount will greatly assist the optimization algorithm.
b. What is the probability that the hedge fund wins the auction if it bids the amount that maximizes its expected return?
 a. Construct a spreadsheet simulation model for this auction. Use a discrete uniform distribution between the minimum and maximum number of bidders in the 10 observed auctions to model the number of bidders in the Jackson Pollock auction. Fit a realistic distribution to the bid data to generate values of competing bid amounts. Use ASP to apply simulation optimization to determine the hedge fund's bid amount that maximizes the expected return = P(winning auction)*(185 - bid amount). Hint: Placing reasonable bounds on the highest and lowest possible bid amount will greatly assist the optimization algorithm.
a. Construct a spreadsheet simulation model for this auction. Use a discrete uniform distribution between the minimum and maximum number of bidders in the 10 observed auctions to model the number of bidders in the Jackson Pollock auction. Fit a realistic distribution to the bid data to generate values of competing bid amounts. Use ASP to apply simulation optimization to determine the hedge fund's bid amount that maximizes the expected return = P(winning auction)*(185 - bid amount). Hint: Placing reasonable bounds on the highest and lowest possible bid amount will greatly assist the optimization algorithm. b. What is the probability that the hedge fund wins the auction if it bids the amount that maximizes its expected return?

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
45
A football tournament is conducted between Team-A and Team-B of a college and the winner being the first team to win four games of seven games. The probability that Team-A wins each game are as follows:
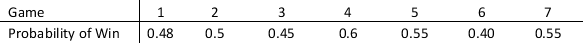 a. Set up a spreadsheet simulation model in which whether Team-A wins each game is a random variable.
a. Set up a spreadsheet simulation model in which whether Team-A wins each game is a random variable.
b. What is the probability that the Team- A win the tournament?
c. What is the average number of games played regardless of winner?
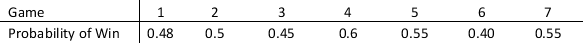 a. Set up a spreadsheet simulation model in which whether Team-A wins each game is a random variable.
a. Set up a spreadsheet simulation model in which whether Team-A wins each game is a random variable.b. What is the probability that the Team- A win the tournament?
c. What is the average number of games played regardless of winner?

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
46
An Investment firm offers free financial planning seminars at major hotels for groups of 30 individuals. Each seminar costs them $4,000 and the average first-year commission for each new enrollment is $6,000. The firm estimates that for each individual attending the seminar, there is a 0.05 probability that he/she will enroll. a. Determine the equation for computing the profit per seminar, given values of the relevant parameters.
b. Construct a spreadsheet simulation model to analyze the profitability of the seminars. Would you recommend the investment firm to continue running the seminars?
b. Construct a spreadsheet simulation model to analyze the profitability of the seminars. Would you recommend the investment firm to continue running the seminars?

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
47
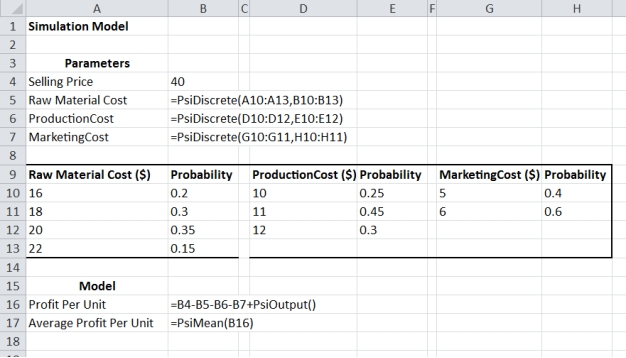
Sunseel Industries produces different types of raw materials and it is interested in using simulation to estimate the profit per unit for its new product X. The selling price for the product will be $40 per unit. Probability distributions for the raw material cost, the production cost, and the marketing cost are estimated as follows:
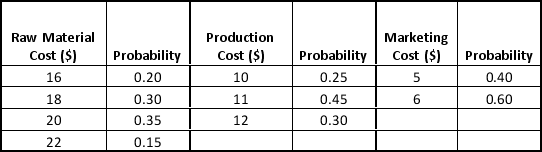 a. Compute profit per unit for the base case, worst case, and best case.
a. Compute profit per unit for the base case, worst case, and best case.
b. Construct a simulation model to estimate the mean profit per unit.
c. Management believes the project may not be sustainable if the profit per unit is less than $2. Use simulation to estimate the probability the profit per unit will be less than $2.
 a. Compute profit per unit for the base case, worst case, and best case.
a. Compute profit per unit for the base case, worst case, and best case.b. Construct a simulation model to estimate the mean profit per unit.
c. Management believes the project may not be sustainable if the profit per unit is less than $2. Use simulation to estimate the probability the profit per unit will be less than $2.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
48
A tourist bus can accommodate 80 people and currently books up to 80 reservations. Past data shows that the tourist bus always accommodates all 80 reservations but that, on average, two people do not show up. To capture additional profit, the travel agent is considering an overbooking strategy in which he would accept 82 reservations even though the tourist bus can accommodate only 80 people. The travel agent believes that he will be able to always book all 82 reservations. The probability distribution for the number of people showing up when 82 reservations are accepted is estimated as follows:
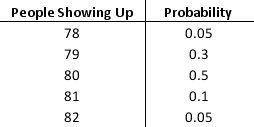
The travel agent receives a marginal profit of $110 for each passenger who books a reservation (regardless whether they show up). The travel agent will also incur a cost for any passenger denied seating on the bus. This cost covers added expenses of rescheduling the passenger as well as loss of goodwill, estimated to be $160 per passenger. Develop a spreadsheet simulation model for this overbooking system. Simulate the number of passengers showing up. a. What is the average net profit for each tourist bus with the overbooking strategy?
b. What is the probability that the net profit with the overbooking strategy will be less than the net profit without overbooking (80*$110 = $8,800)?
c. Explain how your simulation model could be used to evaluate other overbooking levels such as 81, 83, and 84 and for recommending a best overbooking strategy.

The travel agent receives a marginal profit of $110 for each passenger who books a reservation (regardless whether they show up). The travel agent will also incur a cost for any passenger denied seating on the bus. This cost covers added expenses of rescheduling the passenger as well as loss of goodwill, estimated to be $160 per passenger. Develop a spreadsheet simulation model for this overbooking system. Simulate the number of passengers showing up. a. What is the average net profit for each tourist bus with the overbooking strategy?
b. What is the probability that the net profit with the overbooking strategy will be less than the net profit without overbooking (80*$110 = $8,800)?
c. Explain how your simulation model could be used to evaluate other overbooking levels such as 81, 83, and 84 and for recommending a best overbooking strategy.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
49
A company has produced a new battery with an estimated mean lifetime of 60 hours. Management also believes that the standard deviation is 4.5 hours and that battery hours are normally distributed. To promote the new battery, the management has offered to refund some money if the battery fails to reach 50 hours before the battery needs to be recharged. Specifically, for batteries with a lifetime below 50 hours, the management will refund a customer $50 per hour short of 50 hours. a. For each battery sold, what is the expected cost of the promotion? b. What hours should the company set the promotion claim if it wants the expected cost to be $0.50?

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
50
Team X is scheduled to play against Team Y in an upcoming game in Baseball's World Series. Assume that each player's point production can be represented as an integer uniform variable with the ranges provided in the following table:
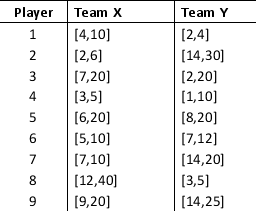 a. Develop a spreadsheet model that simulates the points scored by each team.
a. Develop a spreadsheet model that simulates the points scored by each team.
b. What are the average and standard deviation of points scored by Team X? What is the shape of the distribution of points scored by Team X?
c. What are the average and standard deviation of points scored by Team Y? What is the shape of the distribution of points scored by Team Y?
d. Let Point Differential = Team X points - Team Y points. What is the average point differential between the two teams? What is the standard deviation in the point differential? What is the shape of the point differential distribution?
e. What is the probability that the Team X scores more points than the Team Y?
 a. Develop a spreadsheet model that simulates the points scored by each team.
a. Develop a spreadsheet model that simulates the points scored by each team.b. What are the average and standard deviation of points scored by Team X? What is the shape of the distribution of points scored by Team X?
c. What are the average and standard deviation of points scored by Team Y? What is the shape of the distribution of points scored by Team Y?
d. Let Point Differential = Team X points - Team Y points. What is the average point differential between the two teams? What is the standard deviation in the point differential? What is the shape of the point differential distribution?
e. What is the probability that the Team X scores more points than the Team Y?

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
51
Worst-Case scenario:
Profit = 40 - 22 - 12- 6 = $0/unit
Best-Case scenario:
Profit = 40 - 16 - 10 - 5 = $9/unit
b. The average profit from the simulation model (see below) should be approximately $4.45.
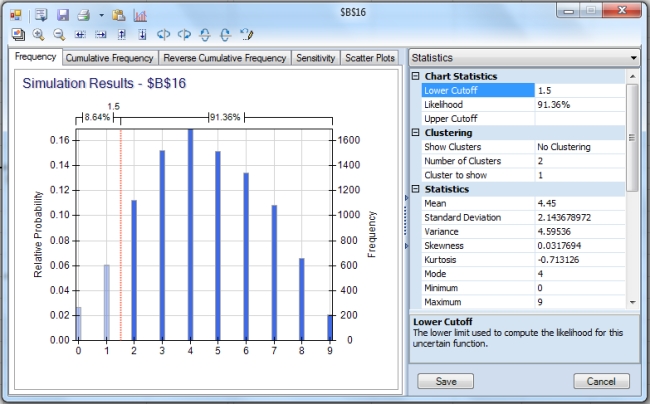
c. As seen in the chart below, there is approximately a 0.09 probability that profit per unit will be less than $2.
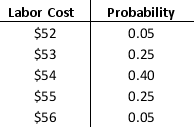
Salemach Corporation is a start-up company that manufactures simple machines. It is interested in analyzing the profit from a new machine. It estimates that the selling price will be $150 per unit and the setup and advertising costs will total $250,000. The company estimates that the per unit raw material cost is uniformly distributed between $50 and $80 and are equally likely. The demand is normally distributed with a mean of 12,000 units and a standard deviation of 3000 units. The probability distribution for a range of labor cost per unit is given below.
 a. Obtain estimates for the mean profit, maximum profit, minimum profit, and standard deviation of profit.
a. Obtain estimates for the mean profit, maximum profit, minimum profit, and standard deviation of profit.
b. What is your estimate of the probability of a loss?
Profit = 40 - 22 - 12- 6 = $0/unit
Best-Case scenario:
Profit = 40 - 16 - 10 - 5 = $9/unit
b. The average profit from the simulation model (see below) should be approximately $4.45.

c. As seen in the chart below, there is approximately a 0.09 probability that profit per unit will be less than $2.

Salemach Corporation is a start-up company that manufactures simple machines. It is interested in analyzing the profit from a new machine. It estimates that the selling price will be $150 per unit and the setup and advertising costs will total $250,000. The company estimates that the per unit raw material cost is uniformly distributed between $50 and $80 and are equally likely. The demand is normally distributed with a mean of 12,000 units and a standard deviation of 3000 units. The probability distribution for a range of labor cost per unit is given below.
 a. Obtain estimates for the mean profit, maximum profit, minimum profit, and standard deviation of profit.
a. Obtain estimates for the mean profit, maximum profit, minimum profit, and standard deviation of profit.b. What is your estimate of the probability of a loss?

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
52
A store is offering a discount on 800 pairs of basketball shoes. The amount of the discount varies and is not revealed to the customer until paying for the shoes. The distribution of discounts is given in the below table:
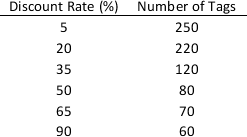
Use the negative binomial distribution to approximate the average number of pairs of shoes that a customer has to buy before purchasing two pair with a discount of at least 50%.

Use the negative binomial distribution to approximate the average number of pairs of shoes that a customer has to buy before purchasing two pair with a discount of at least 50%.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
53
A distributor has generated a rough estimate of aftershave demand at their retails store. The distributor is confident that demand will range from 100 to 650. The following table lists weights for demand values within this range.

The distributor pays a wholesale price of $21 per aftershave and then sells at a retail price of $31. a. Construct a spreadsheet model that computes net profit corresponding to a given level of demand and specified order quantity. Model demand as a random variable with ASP's custom general distribution.
b. Using simulation optimization, determine the order quantity that maximizes expected profit. What is the probability of running out of aftershave at this order quantity?
c. How many aftershaves does the distributor need to order so that the probability of running out of aftershaves is only 25 percent? How much expected profit will the distributor lose if he orders this amount rather than the amount from part b?

The distributor pays a wholesale price of $21 per aftershave and then sells at a retail price of $31. a. Construct a spreadsheet model that computes net profit corresponding to a given level of demand and specified order quantity. Model demand as a random variable with ASP's custom general distribution.
b. Using simulation optimization, determine the order quantity that maximizes expected profit. What is the probability of running out of aftershave at this order quantity?
c. How many aftershaves does the distributor need to order so that the probability of running out of aftershaves is only 25 percent? How much expected profit will the distributor lose if he orders this amount rather than the amount from part b?

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
54
A toy company designs a new toy car this season. The fixed cost to produce the car is $120,000. The variable cost which includes raw materials, production, and shipping costs, is $40 per car. The company will sell the car for $48 each. A distributor has agreed to pay the toy company $12 for each car remaining after the retail selling season. Forecasts are for expected sales of 55,000 toy cars with a standard deviation of 9000. The normal probability distribution is assumed to be a good description of the demand. The management has tentatively decided to produce 55,000 units (the same as average demand), but it wants to conduct an analysis regarding this production quantity before finalizing the decision.
a. Create a what-if spreadsheet model using formula that relate the values of production quantity, demand, sales, revenue from sales, amount of surplus, revenue from sales of surplus, total cost, and net profit. What is the profit corresponding to average demand (55,000 units)?
b. Modeling demand as a normal random variable with a mean of 55,000 and a standard deviation of 9000, simulate the sales of the toy car using a production quantity of 55,000 units. What is the estimate of the average profit associated with the production quantity of 55,000 cars? How does this compare to the profit corresponding to the average demand (as computed in part a)?
c. Before making a final decision on the production quantity, management wants an analysis of a more aggressive 65,000-unit production quantity and a more conservative 45,000-unit production quantity. Run your simulation with these two production quantities. What is the mean profit associated with each?
a. Create a what-if spreadsheet model using formula that relate the values of production quantity, demand, sales, revenue from sales, amount of surplus, revenue from sales of surplus, total cost, and net profit. What is the profit corresponding to average demand (55,000 units)?
b. Modeling demand as a normal random variable with a mean of 55,000 and a standard deviation of 9000, simulate the sales of the toy car using a production quantity of 55,000 units. What is the estimate of the average profit associated with the production quantity of 55,000 cars? How does this compare to the profit corresponding to the average demand (as computed in part a)?
c. Before making a final decision on the production quantity, management wants an analysis of a more aggressive 65,000-unit production quantity and a more conservative 45,000-unit production quantity. Run your simulation with these two production quantities. What is the mean profit associated with each?

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
55
The stock price of Robin Tires, Inc., listed on the Stock Exchange is currently $20. The following probability distribution shows how the price per share is expected to change over a three-month period:
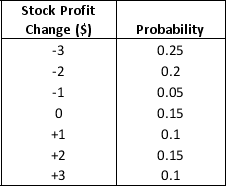 a. Construct a spreadsheet simulation model that computes the value of the stock profit in 3 months, 6 months, 9 months, and 12 months under the assumption that the change in profit over any 3-month period is independent of the change in profit over any other 3-month period.
a. Construct a spreadsheet simulation model that computes the value of the stock profit in 3 months, 6 months, 9 months, and 12 months under the assumption that the change in profit over any 3-month period is independent of the change in profit over any other 3-month period.
b. With the current profit of $20 per share, simulate the profit per share for the next four 3-month periods. What is the average profit in 12 months? What is the standard deviation of the profit in 12 months?
 a. Construct a spreadsheet simulation model that computes the value of the stock profit in 3 months, 6 months, 9 months, and 12 months under the assumption that the change in profit over any 3-month period is independent of the change in profit over any other 3-month period.
a. Construct a spreadsheet simulation model that computes the value of the stock profit in 3 months, 6 months, 9 months, and 12 months under the assumption that the change in profit over any 3-month period is independent of the change in profit over any other 3-month period.b. With the current profit of $20 per share, simulate the profit per share for the next four 3-month periods. What is the average profit in 12 months? What is the standard deviation of the profit in 12 months?

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
56
A store is offering a discount on 800 pairs of basketball shoes. The amount of the discount varies and is not revealed to the customer until paying for the shoes. The distribution of discounts is given in the below table:
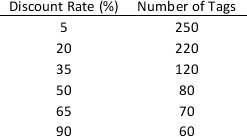
How many pairs of shoes does a customer have to buy so that, on average, he has purchased five containing a 65% or 90% discount? (Hint: Use the hypergeometric distribution in ASP to answer this question.)

How many pairs of shoes does a customer have to buy so that, on average, he has purchased five containing a 65% or 90% discount? (Hint: Use the hypergeometric distribution in ASP to answer this question.)

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
57
A specialty hedge fund is considering the purchase of a Jackson Pollock painting. It estimates the value of the painting to be $185 million. In an auction, both the number of competing bids and the amount of the competing bids is uncertain. The hedge fund has maintained a file summarizing 10 recent art auctions that it believes are similar to the upcoming auction. It is considering a bid of $163 million and would like to evaluate its chances of winning the upcoming auction with this bid.
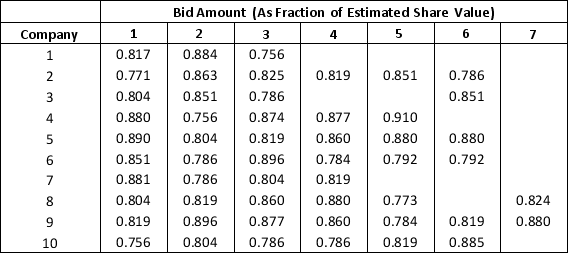 a. Construct a spreadsheet simulation model to determine the likelihood of the hedge fund winning the auction. Use a discrete uniform distribution between the minimum and maximum number of bidders in the 10 observed auctions to model the number of bidders in the Jackson Pollock auction. Fit a realistic distribution to the bid data to generate values of competing bid amounts.
a. Construct a spreadsheet simulation model to determine the likelihood of the hedge fund winning the auction. Use a discrete uniform distribution between the minimum and maximum number of bidders in the 10 observed auctions to model the number of bidders in the Jackson Pollock auction. Fit a realistic distribution to the bid data to generate values of competing bid amounts.
b. For a bid amount of $163 million, estimate the probability of the hedge fund winning the auction?
 a. Construct a spreadsheet simulation model to determine the likelihood of the hedge fund winning the auction. Use a discrete uniform distribution between the minimum and maximum number of bidders in the 10 observed auctions to model the number of bidders in the Jackson Pollock auction. Fit a realistic distribution to the bid data to generate values of competing bid amounts.
a. Construct a spreadsheet simulation model to determine the likelihood of the hedge fund winning the auction. Use a discrete uniform distribution between the minimum and maximum number of bidders in the 10 observed auctions to model the number of bidders in the Jackson Pollock auction. Fit a realistic distribution to the bid data to generate values of competing bid amounts. b. For a bid amount of $163 million, estimate the probability of the hedge fund winning the auction?

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
58
The quality of a device should be examined in the inspection department sequentially in three steps before it is sent to packaging department. The probability distributions for the time required to complete each of the activities are as follows:
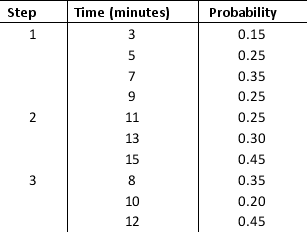
a. Construct a spreadsheet simulation model to estimate the average time spent in inspection department and the standard deviation of the time spent in inspection department.
b. What is the estimated probability that the inspection will be completed in 32 minutes or less?

a. Construct a spreadsheet simulation model to estimate the average time spent in inspection department and the standard deviation of the time spent in inspection department.
b. What is the estimated probability that the inspection will be completed in 32 minutes or less?

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
59
A company has improved its anti-virus program and has released a new version. Assume there is a 0.6 probability that the users of this anti-virus will upgrade the version in any particular year. That is, the upgrade year of the user is a geometric random variable. The revenue generated from the upgrade (when it occurs) follows a normal distribution with a mean of $80,000 and a standard deviation of $22,000.a. Complete a simulation model that analyzes the net present value of the revenue from the user upgrade. Use an annual discount rate of 8 percent.
b. What is the average net present value earned by the company?
c. What is the standard deviation of net present value?
b. What is the average net present value earned by the company?
c. What is the standard deviation of net present value?

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck


