Deck 9: Multiple Regression: Modeling Multivariate Relationships
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/74
Play
Full screen (f)
Deck 9: Multiple Regression: Modeling Multivariate Relationships
1
One limitation to regression is that,due to latent variables,it is hard to know what variable should predict what.
True
A latent variable gives rise to two (or more)others that lack an otherwise causal relationship.This leads to mistakenly basing predictions on the wrong variable.
A latent variable gives rise to two (or more)others that lack an otherwise causal relationship.This leads to mistakenly basing predictions on the wrong variable.
2
Regression is the dominant method of data analysis throughout the natural and social sciences.
True
Regression is the most commonly used method of data analysis.
Regression is the most commonly used method of data analysis.
3
Although regression can verify a relationship between variables,it cannot quantify the nature of that relationship.
False
One of the primary advantages of regression is that it can verify and quantify relationships.
One of the primary advantages of regression is that it can verify and quantify relationships.
4
A histogram will show if the data points are normally distributed.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
5
The Breusch-Pagan test detects whether data is normally distributed.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
6
Autocorrelation occurs when the error does not have a constant variance.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
7
Nonlinear relationships can be examine with ordinary linear regression through transformation functions such as logs,exponents,squares,square roots,and polynomials.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
8
All regression models,including simple linear,binary,ordinal,multinomial logit,rank-ordered,and count,can be viewed as special cases of the general formulation called the General Linear Model.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
9
Standardized residuals are useful in seeing whether there are any strong outliers.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
10
In regression analysis,the F-test tells you if all of the variables taken together help explain the variation in the dependent variable.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
11
Substantial autocorrelation within data can be corrected for with myriad techniques,such as transformations and dummy variables.It should therefore not call into question the regression model itself.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
12
Regression,as a general method,is so versatile,through transformations and special cases,that it can never be overused.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
13
Each independent coefficient ( )in a regression model will show the impact on the dependent variable of a one-unit change in the corresponding independent variable,if all of the other variables are held constant.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
14
One of the limitations of regression is that it can be used only for linear relationships.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
15
The problem with heteroscedasticity is that researchers tend to be underconfident,i.e.they must make statements as if the data is worse than it actually is.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
16
Regression presumes the following theoretical model for the population:
where Y is the dependent variable,the Xs are the independent variables,the ?s are the coefficients of the independent variables,and ? is the error.
where Y is the dependent variable,the Xs are the independent variables,the ?s are the coefficients of the independent variables,and ? is the error.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
17
Of the two main methods underlying nearly all of mathematical reasoning,statistics (particularly regression)is used when dealing with quantities that are certain.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
18
One way to correct for heteroscedasticity is to transform either the independent variables or the dependent variable using logarithms.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
19
The t-test is the first thing that should be checked in a regression output.If it is not significant,then the entire model is not providing sufficient explanatory power.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
20
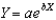 is the form of a geometric relationship.
is the form of a geometric relationship.
Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
21
_______________ occurs when the error does not have a constant variance.
A) Non-normality
B) Heteroscedasticity
C) Autocorrelation
D) Multicollinearity
A) Non-normality
B) Heteroscedasticity
C) Autocorrelation
D) Multicollinearity

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
22
The best way to see if heteroscedasticity is present is to
A) plot the residuals against the dependent variables and examine at them
B) plot the residuals against each of the independent variables and examine them
C) use the Kolmogorov-Smirnov or Shapiro-Wilk test supplied in most computer statistical programs
D) apply a logarithmic transformation
A) plot the residuals against the dependent variables and examine at them
B) plot the residuals against each of the independent variables and examine them
C) use the Kolmogorov-Smirnov or Shapiro-Wilk test supplied in most computer statistical programs
D) apply a logarithmic transformation

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
23
Polynomial regression is a robust method that should be among the first transformations to try on nonlinear data.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
24
All of the following statements about regression are true except:
A) Regression is a way to put a line through a group of data points.
B) Regression is a method for testing the validity of relationships.
C) Regression is method of verifying causal relationships.
D) Regression is a flexible methodology for measuring how things influence one another.
A) Regression is a way to put a line through a group of data points.
B) Regression is a method for testing the validity of relationships.
C) Regression is method of verifying causal relationships.
D) Regression is a flexible methodology for measuring how things influence one another.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
25
For multiple linear regression,researchers want to examine the r2 instead of the adjusted r2 because the r2 is not as easily fooled by additional independent variables.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
26
Due to assumptions in linear regression about the distribution and mean of the error,the only population parameter that will need to be estimated to understand the extent of error is the
A) autocorrelation of the error
B) standard deviation of the error
C) coefficient of determination
D) coefficient of variation
A) autocorrelation of the error
B) standard deviation of the error
C) coefficient of determination
D) coefficient of variation

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
27
Predicting one dependent variable based on many independent variables is called
A) simple linear regression
B) bivariate regression
C) multiple regression
D) multinomial regression
A) simple linear regression
B) bivariate regression
C) multiple regression
D) multinomial regression

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
28
For linear regression,the assumption is made that the error term is
A) normally distributed with a mean of 1
B) normally distributed with a mean of 0
C) the sum of the standard deviations of all of the values
D) the sum-of-squares explained by the regression model
A) normally distributed with a mean of 1
B) normally distributed with a mean of 0
C) the sum of the standard deviations of all of the values
D) the sum-of-squares explained by the regression model

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
29
To determine if the fit of a regression equation is larger than the error,the _______________ is used.
A) F-test
B) t-test
C) chi-square
D) significance level
A) F-test
B) t-test
C) chi-square
D) significance level

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
30
If the error for one data point can help predict the value of the error in nearby data points,then the problem is
A) non-normality
B) heteroscedasticity
C) autocorrelation
D) multicollinearity
A) non-normality
B) heteroscedasticity
C) autocorrelation
D) multicollinearity

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
31
_______________ occurs when a number of potential predictors in a regression model are highly correlated.
A) Non-normality
B) Multicollinearity
C) Heteroscedasticity
D) Autocorrelation
A) Non-normality
B) Multicollinearity
C) Heteroscedasticity
D) Autocorrelation

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
32
To determine if a regression model is useful,the
A) fit (or prediction) should be bigger, on average, than "error"
B) coefficients (the b's) should be clearly different from zero
C) p value should be greater than the F-test value
D) all of the above
E) both a and b
A) fit (or prediction) should be bigger, on average, than "error"
B) coefficients (the b's) should be clearly different from zero
C) p value should be greater than the F-test value
D) all of the above
E) both a and b

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
33
Standardized residuals are used to determine if there are any potential outliers in the data.Data points that are greater that have residuals higher than _______________ in magnitude should be examined,unless the data set is very large.
A) 1
B) 3
C) 5
D) 10
A) 1
B) 3
C) 5
D) 10

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
34
The value of r2 will always increase when adding additional variables to a multiple linear regression equation.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
35
To determine if the regression coefficients (b's)in a regression model are significantly different from zero,the _______________ is used.
A) F-test
B) t-test
C) chi-square
D) significance level
A) F-test
B) t-test
C) chi-square
D) significance level

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
36
If the dependent variable is nominal data,then you would use Poisson regression for the regression analysis

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
37
All of the following are limitations of regression except
A) regression assumptions are usually violated
B) almost nothing is really linear
C) latent variables may be present
D) insufficient predictor variables
A) regression assumptions are usually violated
B) almost nothing is really linear
C) latent variables may be present
D) insufficient predictor variables

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
38
_______________ occurs when the error is not normally distributed.
A) Non-normality
B) Heteroscedasticity
C) Autocorrelation
D) Multicollinearity
A) Non-normality
B) Heteroscedasticity
C) Autocorrelation
D) Multicollinearity

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
39
In binary regression,it would be inappropriate to put a line through the observations in a data plot,because the values of the independent variables can only be 0 or 1.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
40
Violating the underlying assumptions of regression can lead to all of the following problems except
A) non-normality
B) standardized residuals
C) heteroscedasticity
D) autocorrelation
A) non-normality
B) standardized residuals
C) heteroscedasticity
D) autocorrelation

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
41
If the dependent variable is a nominal scale,then the proper regression model to use is
A) multinomial regression
B) probit model
C) ordered logit model
D) linear regression after a chi square transformation
E) count regression
A) multinomial regression
B) probit model
C) ordered logit model
D) linear regression after a chi square transformation
E) count regression

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
42
The model used most often in marketing that includes item-specific information is referred to as the
A) Gumbel Logit model (GLM)
B) Multinomial Logit model (MNL)
C) Guadagni & Little Logit model (GLLM)
D) Kaiser Probit model (KPM)
A) Gumbel Logit model (GLM)
B) Multinomial Logit model (MNL)
C) Guadagni & Little Logit model (GLLM)
D) Kaiser Probit model (KPM)

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
43
Identifying nonlinear relationships between variables is accomplished by transforming one or more variables and then estimating the fit with
A) linear regression
B) curvilinear regression
C) multicollinearity analysis
D) a close examination of the residuals plot
A) linear regression
B) curvilinear regression
C) multicollinearity analysis
D) a close examination of the residuals plot

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
44
The error term in a binary regression using a logit model is assumed to be a
A) normal distribution
B) Gumbel distribution
C) bivariate distribution
D) Poisson distribution
A) normal distribution
B) Gumbel distribution
C) bivariate distribution
D) Poisson distribution

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
45
Use the regression output below to answer the following questions.
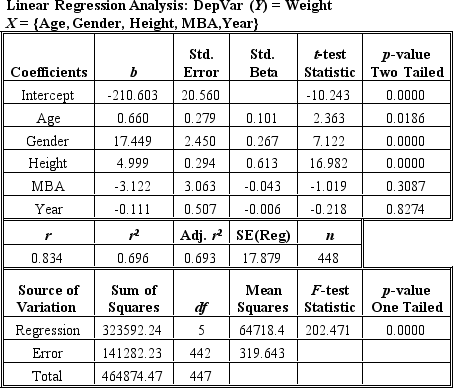
Which statistics should one look at to determine which of the independent variables are most significant in the regression?
A) r2 and adj r2
B) sum of squares and F-test
C) F-test and p
D) t-test and p

Which statistics should one look at to determine which of the independent variables are most significant in the regression?
A) r2 and adj r2
B) sum of squares and F-test
C) F-test and p
D) t-test and p

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
46
If the dependent variable is an ordinal scale,then the proper regression model to use is the
A) linear regression model with geometric transformation of the dependent variable
B) ordered probit model
C) ordered logit model
D) any of the above
E) either b or c
A) linear regression model with geometric transformation of the dependent variable
B) ordered probit model
C) ordered logit model
D) any of the above
E) either b or c

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
47
Which list of common variables below would be examples of continuous data?
A) price, time, volume, length, sales
B) gender, coupon used, college degree, promotion (yes/no)
C) education level, age group, survey scale response (e.g., 1 to 7)
D) ethnic group, product category, SKU, payment method
A) price, time, volume, length, sales
B) gender, coupon used, college degree, promotion (yes/no)
C) education level, age group, survey scale response (e.g., 1 to 7)
D) ethnic group, product category, SKU, payment method

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
48
The test for autocorrelation is the
A) Durbin-Watson
B) Kolmogorov-Smirnov
C) Shapiro-Wilk
D) Anderson-Darling
A) Durbin-Watson
B) Kolmogorov-Smirnov
C) Shapiro-Wilk
D) Anderson-Darling

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
49
_______________ takes both binary and interval data and produces probabilities of an outcome,such as purchase probabilities and market share projections,as functions of the marketing mix.
A) The weighted least squares model
B) Logistic regression
C) The Breusch-Pagan model
D) The discrete choice model
A) The weighted least squares model
B) Logistic regression
C) The Breusch-Pagan model
D) The discrete choice model

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
50
When using rank-ordered data,the regression model that will be used is the
A) multinomial logit regression model
B) discrete choice model
C) exploded logit regression model
D) ordered probit model
A) multinomial logit regression model
B) discrete choice model
C) exploded logit regression model
D) ordered probit model

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
51
Use the regression output below to answer the following questions.

Which variable(s)is/are (a)significant,strong predictor(s)of Weight in the regression above?
A) Age and Height
B) Gender only
C) Height only
D) Age, Height, Gender, MBA and Year
E) Height and Gender

Which variable(s)is/are (a)significant,strong predictor(s)of Weight in the regression above?
A) Age and Height
B) Gender only
C) Height only
D) Age, Height, Gender, MBA and Year
E) Height and Gender

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
52
In multiple regression,the intercept is the value of Y when
A) all of the independent variables are 0
B) the dependent variables is 0
C) all of the significant independent variables are set to 1
D) all of the coefficients are set to 1
A) all of the independent variables are 0
B) the dependent variables is 0
C) all of the significant independent variables are set to 1
D) all of the coefficients are set to 1

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
53
Which list of common variables below would be examples of ordinal data?
A) price, time, volume, length, sales
B) gender, coupon used, college degree, promotion (yes/no)
C) education level, age group, survey scale response (e.g., 1 to 7)
D) ethnic group, product category, SKU, payment method
A) price, time, volume, length, sales
B) gender, coupon used, college degree, promotion (yes/no)
C) education level, age group, survey scale response (e.g., 1 to 7)
D) ethnic group, product category, SKU, payment method

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
54
If the dependent variable is count data,the regression model that will be used is the
A) multinomial logit regression model
B) discrete choice model
C) exploded logit regression model
D) Poisson regression model
A) multinomial logit regression model
B) discrete choice model
C) exploded logit regression model
D) Poisson regression model

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
55
Use the regression output below to answer the following questions.

According to the regression output above,if Age is increased by one year,what will the impact be on Weight?
A) 0.660 lb. increase
B) 0.279 lb. increase
C) 2.363 lb. increase
D) cannot be determined

According to the regression output above,if Age is increased by one year,what will the impact be on Weight?
A) 0.660 lb. increase
B) 0.279 lb. increase
C) 2.363 lb. increase
D) cannot be determined

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
56
In binary regression,probability data for predicting binary variables is transformed using
A) an exponential transformation
B) a geometric transformation
C) the logarithm of the odds
D) dummy variables
A) an exponential transformation
B) a geometric transformation
C) the logarithm of the odds
D) dummy variables

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
57
If the dependent variable in a regression model is continuous interval data,the analysis should employ
A) multiple linear regression
B) binary regression
C) Poisson or count regression
D) multinomial regression
E) ordinal regression
A) multiple linear regression
B) binary regression
C) Poisson or count regression
D) multinomial regression
E) ordinal regression

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
58
Use the regression output below to answer the following questions.

In using Poisson regression,the researcher also must know
A) both the observed count and the number of opportunities
B) the relative percentages of each outcome
C) the distribution of the population
D) both the variance and the population mean

In using Poisson regression,the researcher also must know
A) both the observed count and the number of opportunities
B) the relative percentages of each outcome
C) the distribution of the population
D) both the variance and the population mean

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
59
Use the regression output below to answer the following questions.

According to the regression output above,which of the following statements most accurately summarizes what can be said,for the entire population,about the weight of individuals with an MBA (MBA=1)versus the weight of individuals without an MBA (MBA=0)?
A) They weigh on average 3.122 pounds less than individuals who do not have an MBA.
B) They weigh on average 3.122 pounds more than individuals who do not have an MBA.
C) Their weights are roughly the same.
D) The variable is not a significant predictor, so, even though its coefficient estimate is -3.222, we cannot assume it has an impact on weight.

According to the regression output above,which of the following statements most accurately summarizes what can be said,for the entire population,about the weight of individuals with an MBA (MBA=1)versus the weight of individuals without an MBA (MBA=0)?
A) They weigh on average 3.122 pounds less than individuals who do not have an MBA.
B) They weigh on average 3.122 pounds more than individuals who do not have an MBA.
C) Their weights are roughly the same.
D) The variable is not a significant predictor, so, even though its coefficient estimate is -3.222, we cannot assume it has an impact on weight.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
60
Based on the binary regression output above,which of the independent variable(s)are significant predictors of Gender?
A) Age and Weight
B) Age and Height
C) Height and Weight
D) Age, Height and Weight
E) all of the variables are significant
F) none of the variables is significant
A) Age and Weight
B) Age and Height
C) Height and Weight
D) Age, Height and Weight
E) all of the variables are significant
F) none of the variables is significant

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
61
Based on the output above,the LOGIT model correctly predicted the female gender
A) 87 percent of the time
B) 91.3 percent of the time
C) 89.5 percent of the time
D) cannot be determined
A) 87 percent of the time
B) 91.3 percent of the time
C) 89.5 percent of the time
D) cannot be determined

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
62
Which independent variable is,taken by itself,the best predictor of Gender?
A) Age
B) Height
C) Weight
D) cannot be determined
A) Age
B) Height
C) Weight
D) cannot be determined

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
63
Use the regression output below to answer the following questions.
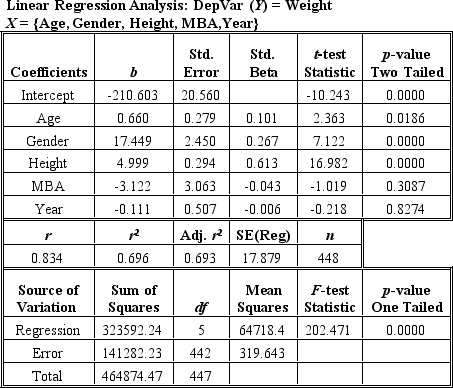
Given that Gender was coded female=0 and male=1,on the average,how much more do males weight than females,"correcting for" (i.e.,including the effects of)all the other variables in the regression?

Given that Gender was coded female=0 and male=1,on the average,how much more do males weight than females,"correcting for" (i.e.,including the effects of)all the other variables in the regression?

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
64
Describe the different types of analysis for the different data types of dependent variable.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
65
Use the regression output below to answer the following questions.
Lingar Reperaidion Anthyis: Dep Var Weight
Ee, Gender, Heifht, MBA, ear
-Write the regression equation for the regression output above.
Lingar Reperaidion Anthyis: Dep Var Weight
Ee, Gender, Heifht, MBA, ear
-Write the regression equation for the regression output above.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
66
The regression output above indicates that a 1 inch increase in Height increases the chance a respondent is male by
A) 39.1 percent
B) 8.2 percent
C) 22.669 percent
D) 47.8 percent
A) 39.1 percent
B) 8.2 percent
C) 22.669 percent
D) 47.8 percent

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
67
Describe what regression is and what it is used for.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
68
Use the regression output below to answer the following questions.

For each additional inch of Height,how much additional Weight would be added?

For each additional inch of Height,how much additional Weight would be added?

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
69
Explain the problems of non-normality,heteroscedasticity,and autocorrelation and how researchers can detect each.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
70
Describe how transformations can be used to apply linear regression to nonlinear relationships.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
71
Discuss its limitations of regression.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
72
What does the Constant signify in this regression?
A) the probability of Gender=1 when no other variables are changed
B) the average age of males in the sample
C) the average age of females in the sample
D) It does not signify anything useful here.
A) the probability of Gender=1 when no other variables are changed
B) the average age of males in the sample
C) the average age of females in the sample
D) It does not signify anything useful here.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
73
Use the regression output below to answer the following questions.
Lingar Reperaidion Anthyis: Dep Var Weight
Ee, Gender, Heifht, MBA, ear
-Based on the regression printout,what would be the predicted (mean)weight of a female,20 years old,68 inches tall,without an MBA,and in Year 1.
Lingar Reperaidion Anthyis: Dep Var Weight
Ee, Gender, Heifht, MBA, ear
-Based on the regression printout,what would be the predicted (mean)weight of a female,20 years old,68 inches tall,without an MBA,and in Year 1.

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck
74
The regression output above indicates that an additional year in age increases the chance a respondent is male by
A) 11 percent
B) 17.1 percent
C) 0.61 percent
D) 15.8 percent
A) 11 percent
B) 17.1 percent
C) 0.61 percent
D) 15.8 percent

Unlock Deck
Unlock for access to all 74 flashcards in this deck.
Unlock Deck
k this deck


