Deck 13: Game Theory and Strategic Play

Question 1

Scenario: Suppose two soda brands, Mountain Dew and Mello Yello, are trying to decide whether to launch advertising campaigns for their respective products. These decisions will be taken simultaneously, the brands will not be cooperating, and we will assume each brand's strategist knows her own and her opponent's payoffs in all cases. The payoff matrix for this game is shown below.

Refer to the scenario above.Does Mello Yello have a dominant strategy?

A) No.
B) Yes. Regardless of whether Mountain Dew chooses to advertise, Mello Yello's profits are always highest if it advertises.
C) Yes. Regardless of whether Mountain Dew chooses to advertise, Mello Yello's profits are always highest if it does not advertise.
D) Not enough information is provided to answer the question.

Answer 1

Yes. Regardless of whether Mountain Dew chooses to advertise, Mello Yello's profits are always highest if it advertises.

Question 2

A ________ is a complete plan describing how a player will act.

A) strategy
B) payoff
C) hypothesis
D) policy

Answer 2

strategy

Question 3

Which of the following is true of a payoff matrix?

A) It represents only the best response of each player in a game.
B) It takes into account all relevant costs and benefits associated with each action of the players.
C) It shows the payments made to the owners of each factor of production for the production of a good.
D) It does not represent all the costs and benefits associated with the choices of the players.

Answer 3

It takes into account all relevant costs and benefits associated with each action of the players.

Question 4

In a simultaneous-move game,________.

A) each player has to make his choice after knowing his rival's choice
B) each player has to make his choice without knowing his rival's choice
C) there is always more than one Nash equilibrium
D) there is always more than one dominant strategy equilibrium

Question 5

A payoff matrix shows the ________.

A) various combinations of inputs required to produce a good
B) return from each action that players can take in a game
C) different combinations of two goods that can be bought with a given income
D) payments made to the owners of each factor of production for the production of a good

Question 6

Scenario: Suppose two soda brands, Mountain Dew and Mello Yello, are trying to decide whether to launch advertising campaigns for their respective products. These decisions will be taken simultaneously, the brands will not be cooperating, and we will assume each brand's strategist knows her own and her opponent's payoffs in all cases. The payoff matrix for this game is shown below.

Refer to the scenario above.Does Mountain Dew have a dominant strategy?

A) No.
B) Yes. Regardless of whether Mello Yello chooses to advertise, Mountain Dew's profits are always highest if it advertises.
C) Yes. Regardless of whether Mello Yello chooses to advertise, Mountain Dew's profits are always highest if it does not advertise.
D) Not enough information is provided to answer the question.

Question 7

Scenario: Suppose two soda brands, Mountain Dew and Mello Yello, are trying to decide whether to launch advertising campaigns for their respective products. These decisions will be taken simultaneously, the brands will not be cooperating, and we will assume each brand's strategist knows her own and her opponent's payoffs in all cases. The payoff matrix for this game is shown below.

Refer to the scenario above.If both brands choose to advertise,their respective payoffs are ________.

A) profits of 10 cents per can for Mountain Dew and of 5 cents per can for Mello Yello
B) profits of 15 cents per can for Mountain Dew and of 0 cents per can for Mello Yello
C) profits of 6 cents per can for Mountain Dew and of 8 cents per can for Mello Yello
D) profits of 10 cents per can for Mountain Dewand of 2 cents per can for Mello Yello

Question 8

Which of the following is likely to use the concepts of game theory?

A) Household budgeting
B) The exit decisions of competitive firms in the long run
C) International trade negotiation
D) The pricing decision of a firm operating in a competitive market

Question 9

Scenario: Suppose two soda brands, Mountain Dew and Mello Yello, are trying to decide whether to launch advertising campaigns for their respective products. These decisions will be taken simultaneously, the brands will not be cooperating, and we will assume each brand's strategist knows her own and her opponent's payoffs in all cases. The payoff matrix for this game is shown below.

Refer to the scenario above.Is there a dominant strategy equilibrium?

A) No
B) Yes: Mountain Dew does not advertise, Mello Yello does not advertise
C) Yes: Mountain Dew advertises, Mello Yello advertises
D) Yes: Mountain Dew advertises, Mello Yello does not advertise

Question 10

Scenario: Contiguous states often use tax policy to attract residents, firms, and economic activity. These "tax competitions" between states can be modeled with game theory. Suppose New Jersey currently has a state sales tax of 7 percent and Pennsylvania has a state sales tax of 6 percent. The game shown below models the effect of a reduction in each state's sales tax rate to 3 percent on each state's sales tax revenue. Assume the motivation of each state is to maximize tax revenue. The first number in a cell is the payoff to New Jersey; the second number is the payoff to Pennsylvania.

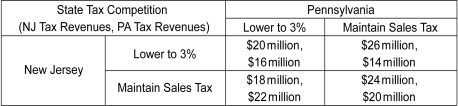
(Source: John Greenwald, "A No-Win War Between the States," Time, April 8, 1996, 44-45.
Refer to the scenario above.Is there a set of payoffs that is superior to the payoffs realized at the dominant strategy equilibrium?

A) No.
B) Yes, New Jersey maintains its sales tax rate, realizing $18 million in tax revenues, and Pennsylvania lowers its sales tax rate, realizing $22 million in tax revenues.
C) Yes, New Jersey maintains its sales tax rate, realizing $24 million in tax revenues, and Pennsylvania also maintains its sales tax rate, realizing $20 million in tax revenues.
D) Yes, New Jersey lowers its sales tax rate, realizing $26 million in tax revenues, and Pennsylvania maintains its sales tax rate, realizing $14 million in tax revenues.

Question 11

A game is called a simultaneous-move game if ________.

A) players choose their actions at the same time
B) one player chooses her action after the other player makes a move
C) players choose mixed strategies to play the game
D) players choose their dominant strategies to play the game

Question 12

Scenario: Contiguous states often use tax policy to attract residents, firms, and economic activity. These "tax competitions" between states can be modeled with game theory. Suppose New Jersey currently has a state sales tax of 7 percent and Pennsylvania has a state sales tax of 6 percent. The game shown below models the effect of a reduction in each state's sales tax rate to 3 percent on each state's sales tax revenue. Assume the motivation of each state is to maximize tax revenue. The first number in a cell is the payoff to New Jersey; the second number is the payoff to Pennsylvania.

(Source: John Greenwald, "A No-Win War Between the States," Time, April 8, 1996, 44-45.
Refer to the scenario above.Is there a dominant strategy equilibrium?

A) No.
B) Yes, New Jersey lowers its sales tax rate to 3 percent and Pennsylvania maintains its sales tax rate.
C) Yes, both New Jersey and Pennsylvania maintain their sales tax rates.
D) Yes, both New Jersey and Pennsylvania lower their sales tax rates to 3 percent.

Question 13

Scenario: Contiguous states often use tax policy to attract residents, firms, and economic activity. These "tax competitions" between states can be modeled with game theory. Suppose New Jersey currently has a state sales tax of 7 percent and Pennsylvania has a state sales tax of 6 percent. The game shown below models the effect of a reduction in each state's sales tax rate to 3 percent on each state's sales tax revenue. Assume the motivation of each state is to maximize tax revenue. The first number in a cell is the payoff to New Jersey; the second number is the payoff to Pennsylvania.

(Source: John Greenwald, "A No-Win War Between the States," Time, April 8, 1996, 44-45.
Refer to the scenario above.Does New Jersey have a dominant strategy?

A) No.
B) Yes. Regardless of whether Pennsylvania decides to lower its sales tax rate, New Jersey will always gain more revenue by lowering their sales tax rate to 3 percent.
C) Yes. Regardless of whether Pennsylvania decides to lower its sales tax rate, New Jersey will always gain more revenue by maintaining their sales tax rate at 7 percent.
D) Not enough information is provided to answer the question.

Question 14

Which of the following games is a simultaneous-move game?

A) In a Senate race, an incumbent senator (from a rightist party) runs against a challenger (from a leftist party)
B) The game of chess
C) The rock-paper-scissor game
D) The game of poker

Question 15

Which of the following games is not a simultaneous-move game?

A) A tourist bargains with a local vendor for the price of souvenirs on a beach in the Dominican Republic.
B) Two bidders place a bid in a sealed envelope during an auction. The highest bidder wins the auction.
C) Two drivers drive toward each other on a collision course; the first to swerve loses.
D) Ann and Bob must meet at 8 P.M. However, there are two possible meeting points, and they cannot communicate before the meeting.

Question 16

Scenario: Contiguous states often use tax policy to attract residents, firms, and economic activity. These "tax competitions" between states can be modeled with game theory. Suppose New Jersey currently has a state sales tax of 7 percent and Pennsylvania has a state sales tax of 6 percent. The game shown below models the effect of a reduction in each state's sales tax rate to 3 percent on each state's sales tax revenue. Assume the motivation of each state is to maximize tax revenue. The first number in a cell is the payoff to New Jersey; the second number is the payoff to Pennsylvania.

(Source: John Greenwald, "A No-Win War Between the States," Time, April 8, 1996, 44-45.
Refer to the scenario above.Does Pennsylvania have a dominant strategy?

A) No.
B) Yes. Regardless of whether New Jersey decides to lower its sales tax rate, Pennsylvania will always gain more revenue by lowering their sales tax rate to 3 percent.
C) Yes. Regardless of whether New Jersey decides to lower its sales tax rate, Pennsylvania will always gain more revenue by maintaining their sales tax rate at 6 percent.
D) Not enough information is provided to answer the question.

Question 17

Which of the following is true of a simultaneous-move game?

A) Players choose their actions after knowing the action of the first player.
B) All relevant benefits and costs of each action are taken into account.
C) It involves strategic interactions among a large number of players.
D) It cannot be represented by a payoff matrix.

Question 18

Game theory is the study of ________.

A) policy analysis
B) strategic interactions
C) program evaluation
D) irrational decision making

Question 19

________ helps an individual make economic decisions when the individual's behavior determines the payoffs to others.

A) Empiricism
B) Macroeconomics
C) Game theory
D) Public economics

Question 20

________ describes an individual's optimal actions in settings where interactions with others determine her well-being.

A) Game theory
B) Utility optimization
C) Strategic equilibrium
D) Cost-benefit analysis

Question 21

Scenario: Company A and Company B are considering spending a certain sum of money to advertise their new range of products. If Company A chooses to advertise while Company B does not, Company A's annual sales will increase by $5 million, while Company B's sales will remain unchanged. If Company B chooses to advertise while Company A does not, Company B's annual sales will increase by $5 million, while Company A will not experience any change in its sales. If both the companies decide to advertise, their sales will increase sales by $2 million each, and if neither of them spends on advertisement, their sales will remain unchanged.
Refer to the scenario above.Suppose the cost of advertising in this industry is very high and each company will incur a cost of $3 million annually if they choose to advertise.Which of the following is true in this case?

A) Company A's best response is to advertise if Company B advertises.
B) Company B's best response is to advertise irrespective of what Company A does.
C) Company A's dominant strategy is to advertise.
D) This game does not have a dominant strategy equilibrium.

Question 22

Scenario: Rita and Mike have been caught cheating on an examination. They are taken to separate rooms for interrogation. Their payoff matrix is given below. The first outcome listed in each cell is the payoff to the row player, and the second outcome listed is the payoff to the column player.

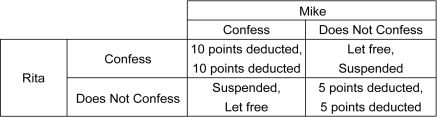
Refer to the scenario above.Which of the following is true?

A) Mike's best response is to hold out if Rita confesses.
B) Rita's best response is to hold out if she expects Mike not to confess
C) Rita's best response is not to confess irrespective of what Mike does.
D) Mike's best response is to confess irrespective of what Rita does.

Question 23

A best response is ________.

A) one player's optimal action choice taken irrespective of the action of the other player
B) one player's optimal action choice taking the other player's action as given
C) an action choice that always results in a zero payoff to the opponent
D) an action choice that results in equal payoffs to all the players in a game

Question 24

The prisoners' dilemma is an example of a(n)________ game.

A) simultaneous-move
B) extensive-form
C) zero-sum
D) mixed-strategy

Question 25

Scenario: Rita and Mike have been caught cheating on an examination. They are taken to separate rooms for interrogation. Their payoff matrix is given below. The first outcome listed in each cell is the payoff to the row player, and the second outcome listed is the payoff to the column player.

Refer to the scenario above.Which of the following is likely to happen if Rita does not confess?

A) Both of them will be let free.
B) Mike will be let free, while Rita will be suspended.
C) 10 points will be deducted from their respective scores.
D) 10 points will be deducted from Rita's score, while Mike will be suspended.

Question 26

Which of the following statements is true?

A) In any game, the best response of a player is also her dominant strategy.
B) The best response of a player is not always her dominant strategy.
C) The prisoners' dilemma game is an example of a zero-sum game.
D) The prisoners' dilemma game is an example of an extensive-form game.

Question 27

Scenario: Rita and Mike have been caught cheating on an examination. They are taken to separate rooms for interrogation. Their payoff matrix is given below. The first outcome listed in each cell is the payoff to the row player, and the second outcome listed is the payoff to the column player.

Refer to the scenario above.What will likely be the outcome of this game?

A) Mike will confess, while Rita will not confess.
B) Rita will confess, while Mike will not confess.
C) Neither of them will confess.
D) Both of them will confess.

Question 28

Scenario: The payoff matrix given below shows the payoffs to two rival firms in millions of U.S. dollars for each strategy they choose. The first number listed in each cell is the payoff to the row player, and the second number listed is the payoff to the column player.

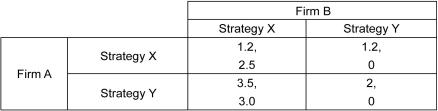
Refer to the scenario above.Which of the following is true?

A) Firm A's dominant strategy is Strategy X.
B) Firm B's dominant strategy is Strategy Y.
C) Firm A is better off choosing Strategy X when Firm B chooses Strategy Y.
D) Firm B is better off choosing Strategy X when Firm A chooses Strategy Y.

Question 29

Scenario: Two rival firms are considering sponsoring an event. Each firm believes that sponsoring the event will increase its sales by a certain percentage. The payoff matrix showing the increase in sales for the firms is given below. The first number listed in each cell is the payoff to the row player, and the second number listed is the payoff to the column player.

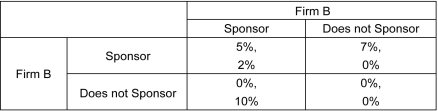
Refer to the scenario above.What is likely to be the impact on Firm B's sales if Firm B decides to sponsor the event?

A) A 5 percent increase in sales
B) A 2 percent increase in sales
C) A 7 percent increase in sales
D) A 0 percent increase in sales

Question 30

Scenario: Company A and Company B are considering spending a certain sum of money to advertise their new range of products. If Company A chooses to advertise while Company B does not, Company A's annual sales will increase by $5 million, while Company B's sales will remain unchanged. If Company B chooses to advertise while Company A does not, Company B's annual sales will increase by $5 million, while Company A will not experience any change in its sales. If both the companies decide to advertise, their sales will increase sales by $2 million each, and if neither of them spends on advertisement, their sales will remain unchanged.
Refer to the scenario above.If the cost of advertising is negligible,what will be the outcome of this game?

A) Company A will advertise its products while Company B will not advertise.
B) Company B will advertise, while Company A will not advertise.
C) Both the companies will advertise their products.
D) Neither of the companies will advertise its products.

Question 31

A dominant strategy ________.

A) always results in equal payoffs to all the players in a game
B) always results in a zero payoff to the opponent
C) results in a high payoff irrespective of the strategy chosen by the other player
D) always results in a low payoff irrespective of the strategy chosen by the other player

Question 32

Scenario: Two rival firms are considering sponsoring an event. Each firm believes that sponsoring the event will increase its sales by a certain percentage. The payoff matrix showing the increase in sales for the firms is given below. The first number listed in each cell is the payoff to the row player, and the second number listed is the payoff to the column player.

Refer to the scenario above.What is likely to be the impact on Firm B's sales if Firm B decides not to sponsor the event?

A) A 5 percent increase in sales
B) A 7 percent increase in sales
C) A 0 percent increase in sales
D) A 2 percent increase in sales

Question 33

Scenario: Two rival firms are considering sponsoring an event. Each firm believes that sponsoring the event will increase its sales by a certain percentage. The payoff matrix showing the increase in sales for the firms is given below. The first number listed in each cell is the payoff to the row player, and the second number listed is the payoff to the column player.

Refer to the scenario above.What is likely to be the impact on Firm A's sales if Firm A decides not to sponsor the event?

A) A 7 percent increase in sales
B) A 0 percent increase in sales
C) A 2 percent increase in sales
D) A 10 percent increase in sales

Question 34

A player has a dominant strategy when ________.

A) her chosen strategy gives her a lower payoff than the other player
B) her chosen strategy matches the best response of the other player in the game
C) she has many best responses to any strategy of the other player in the game
D) she has only one best response to every possible strategy of the other player

Question 35

Scenario: Company A and Company B are considering spending a certain sum of money to advertise their new range of products. If Company A chooses to advertise while Company B does not, Company A's annual sales will increase by $5 million, while Company B's sales will remain unchanged. If Company B chooses to advertise while Company A does not, Company B's annual sales will increase by $5 million, while Company A will not experience any change in its sales. If both the companies decide to advertise, their sales will increase sales by $2 million each, and if neither of them spends on advertisement, their sales will remain unchanged.
Refer to the scenario above.Which of the following is true?

A) Company A should not advertise its products irrespective of what Company B does.
B) Company B should not advertise if Company A decides to advertise its products.
C) Company A should advertise if Company B decides to advertise its products.
D) Company B should not advertise its product irrespective of what Company A does.

Question 36

Scenario: Rita and Mike have been caught cheating on an examination. They are taken to separate rooms for interrogation. Their payoff matrix is given below. The first outcome listed in each cell is the payoff to the row player, and the second outcome listed is the payoff to the column player.

Refer to the scenario above.This is an example of a(n)________.

A) extensive-form game
B) simultaneous-move game
C) zero-sum game
D) mixed-strategy game

Question 37

Which of the following is true of the prisoners' dilemma game?

A) The prisoners' dilemma game has multiple Nash equilibria.
B) There is no dominant strategy equilibrium in the prisoners' dilemma game.
C) The dominant strategy equilibrium in the prisoners' dilemma game is also the Nash equilibrium.
D) The prisoners' dilemma game is an extensive-form game.

Question 38

Scenario: Rita and Mike have been caught cheating on an examination. They are taken to separate rooms for interrogation. Their payoff matrix is given below. The first outcome listed in each cell is the payoff to the row player, and the second outcome listed is the payoff to the column player.

Refer to the scenario above.Which of the following is likely to happen if Rita confesses and Mike does not confess?

A) Both of them will be let free.
B) Rita will be let free, while Mike will be suspended.
C) 10 points will be deducted from their respective scores.
D) 10 points will be deducted from Mike's score, while Rita will be suspended.

Question 39

Scenario: Two rival firms are considering sponsoring an event. Each firm believes that sponsoring the event will increase its sales by a certain percentage. The payoff matrix showing the increase in sales for the firms is given below. The first number listed in each cell is the payoff to the row player, and the second number listed is the payoff to the column player.

Refer to the scenario above.What is likely to be the impact on Firm A's sales if Firm A decides to sponsor the event?

A) A 5 percent increase in sales
B) A 2 percent increase in sales
C) A 0 percent increase in sales
D) A 10 percent increase in sales

Question 40

Which of the following is true?

A) A dominant strategy equilibrium always leads to the best outcome for each player.
B) A dominant strategy equilibrium cannot be a Nash equilibrium.
C) A dominant strategy equilibrium is a Nash equilibrium if each player chooses a strategy that is a best response to the strategies of others.
D) A dominant strategy equilibrium occurs if the sum of the players' payoff is zero.

Question 41

Scenario: The payoff matrix given below shows the payoffs to two rival firms in millions of U.S. dollars for each strategy they choose. The first number listed in each cell is the payoff to the row player, and the second number listed is the payoff to the column player.

Refer to the scenario above.In the dominant strategy equilibrium,the payoff to Firm A is ________.

A) $1.2 million
B) $3.0 million
C) $3.5 million
D) $2.5 million

Question 42

The following payoff matrix represents a simultaneous-move game between two players: Alec and Ben. Each player has to choices: Red and Yellow. The first number in each cell is the payoff to Alec, and the second number is the payoff to Ben.

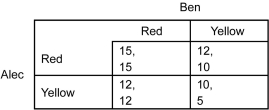
Refer to the table above.Which statement is true?

A) Alec and Ben both choosing Red is the dominant strategy equilibrium of this game.
B) Alec and Ben both choosing Yellow is the dominant strategy equilibrium of this game.
C) Alec choosing Red and Ben choosing Yellow is the dominant strategy equilibrium of this game.
D) There is no dominant strategy equilibrium in this game.

Question 43

Scenario: The payoff matrix given below shows the payoffs to two rival firms in millions of U.S. dollars for each strategy they choose. The first number listed in each cell is the payoff to the row player, and the second number listed is the payoff to the column player.

Refer to the scenario above.In this game,the dominant strategy equilibrium occurs if ________.

A) Firm A chooses Strategy Y and Firm B chooses Strategy X
B) Firm B chooses Strategy Y and Firm B chooses Strategy X
C) both Firm A and Firm B choose Strategy X
D) both Firm A and Firm B choose Strategy Y

Question 44

The following payoff matrix represents a simultaneous-move game between two players: Alec and Ben. Each player has to choices: Red and Yellow. The first number in each cell is the payoff to Alec, and the second number is the payoff to Ben.

Refer to the table above.Which statement is true?

A) Alec and Ben both have a dominant strategy in this game.
B) Only Alec has a dominant strategy in this game.
C) Only Ben has a dominant strategy in this game.
D) Neither Alec nor Ben have a dominant strategy in this game.

Question 45

The following figure depicts four simultaneous-move games. The first element of each payoff cell is the payoff to Player A, and the second element is the payoff to Player B.

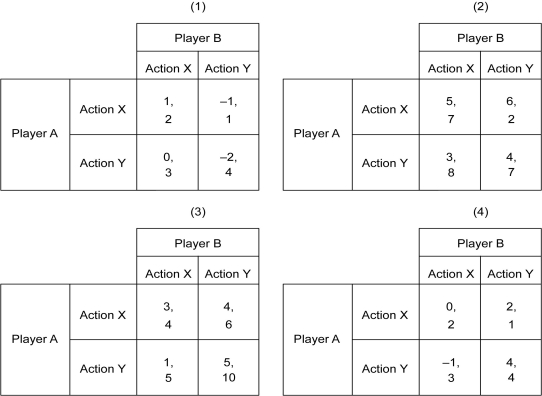
Refer to the figure above.In which of these simultaneous-move games does only player B have a dominant strategy?

A) (1)
B) (2)
C) (3)
D) (4)

Question 46

Scenario: Your friend Joe and you decide to race your new cars. However, both of you are caught speeding by a police patrol. The matrix below shows the respective payoffs for each choice of actions. The first number listed in each cell is the payoff to the row player, and the second number listed is the payoff to the column player.

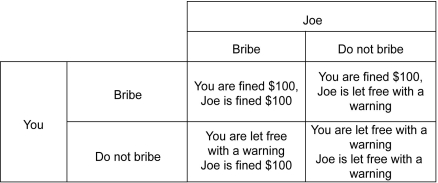
Refer to the scenario above.Suppose a new legislative policy decreases the fine for speeding to $50.This reduction in the fine to $50 ________.

A) makes it profitable for you to bribe
B) makes it profitable for Joe to bribe
C) changes the outcome of the game
D) will not change your dominant strategy

Question 47

Scenario: The payoff matrix given below shows the payoffs to two rival firms in millions of U.S. dollars for each strategy they choose. The first number listed in each cell is the payoff to the row player, and the second number listed is the payoff to the column player.

Refer to the scenario above.In the dominant strategy equilibrium,the payoff to Firm B is ________.

A) $1.2 million
B) $3.0 million
C) $2.5 million
D) $2 million

Question 48

The following payoff matrix represents a simultaneous-move game between two players: John and Trevor. Each player has to choices: Black or White. The first number in each cell is the payoff to John, and the second number is the payoff to Trevor.

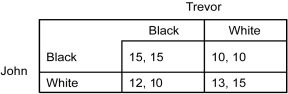
Refer to the table above.If John chooses ________,Trevor is better off choosing ________.And if Trevor chooses ________,John is better off choosing ________.

A) Black; White; Black; White
B) White; White; White; White
C) Black; Black; Black; White
D) Black; White; White; Black

Question 49

Scenario: Miguel and Stephanie are competitors who sell tacos out of their food trucks by the same beach. For each taco they sell, they get a profit of $1.00. Each morning they must decide at which of the three legally permitted locations, A, B, or C, they should park their trucks. The picture below shows the three locations.

In each of the three locations, there are 100 customers per day, and each customer buys a taco from the nearest vendor. If the two trucks are in the same location, then each vendor gets half of the customers. So, for example, if Miguel's truck is in location A, and Stephanie's is also in location A, then half of customers from locations A, B, and C will buy from Miguel's and the other half will buy from Stephanie's, so that each gets a profit of $150. If Miguel's truck is in location A and Stephanie's is in location B, then everyone in location A will buy from Miguel and everyone from locations B and C will buy from Stephanie, so that Miguel's profit is $100 while Stephanie's is $200. If Miguel's truck is in location A and Stephanie's is in location C, then everyone in A plus a half from B will buy from Miguel, and everyone in C plus half from B will buy from Stephanie so that each vendor gets a profit of $150, and so on. The table below is the payoff matrix for this game. The first number in each cell is Miguel's profit, and the second number is Stephanie's profit.

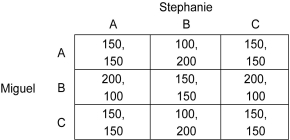
Refer to the scenario above.If Miguel's truck is located at C,what is Stephanie's best response?

A) Location A
B) Location B
C) Location C
D) Location B or C

Question 50

Scenario: Your friend Joe and you decide to race your new cars. However, both of you are caught speeding by a police patrol. The matrix below shows the respective payoffs for each choice of actions. The first number listed in each cell is the payoff to the row player, and the second number listed is the payoff to the column player.

Refer to the scenario above.Which of the following is true?

A) Your dominant strategy is to bribe irrespective of what Joe does.
B) Your dominant strategy is not to bribe irrespective of what Joe does.
C) You should bribe if Joe bribes.
D) Joe should bribe if you bribe.

Question 51

Scenario: Your friend Joe and you decide to race your new cars. However, both of you are caught speeding by a police patrol. The matrix below shows the respective payoffs for each choice of actions. The first number listed in each cell is the payoff to the row player, and the second number listed is the payoff to the column player.

Refer to the scenario above.Which of the following strategy combinations denotes the dominant strategy equilibrium in this case?

A) (Bribe, Bribe)
B) (Bribe, Do not bribe)
C) (Do not bribe, Bribe)
D) (Do not bribe, Do not bribe)

Question 52

Scenario: Miguel and Stephanie are competitors who sell tacos out of their food trucks by the same beach. For each taco they sell, they get a profit of $1.00. Each morning they must decide at which of the three legally permitted locations, A, B, or C, they should park their trucks. The picture below shows the three locations.

In each of the three locations, there are 100 customers per day, and each customer buys a taco from the nearest vendor. If the two trucks are in the same location, then each vendor gets half of the customers. So, for example, if Miguel's truck is in location A, and Stephanie's is also in location A, then half of customers from locations A, B, and C will buy from Miguel's and the other half will buy from Stephanie's, so that each gets a profit of $150. If Miguel's truck is in location A and Stephanie's is in location B, then everyone in location A will buy from Miguel and everyone from locations B and C will buy from Stephanie, so that Miguel's profit is $100 while Stephanie's is $200. If Miguel's truck is in location A and Stephanie's is in location C, then everyone in A plus a half from B will buy from Miguel, and everyone in C plus half from B will buy from Stephanie so that each vendor gets a profit of $150, and so on. The table below is the payoff matrix for this game. The first number in each cell is Miguel's profit, and the second number is Stephanie's profit.

Refer to the scenario above.If Miguel's truck is in location A,what is Stephanie's best response?

A) Location A
B) Location B
C) Location C
D) Location A or C

Question 53

The following figure depicts four simultaneous-move games. The first element of each payoff cell is the payoff to Player A, and the second element is the payoff to Player B.

Refer to the figure above.In which of these simultaneous-move games,do both players A and B have a dominant strategy?

A) (1)
B) (2)
C) (3)
D) (4)

Question 54

Scenario: Miguel and Stephanie are competitors who sell tacos out of their food trucks by the same beach. For each taco they sell, they get a profit of $1.00. Each morning they must decide at which of the three legally permitted locations, A, B, or C, they should park their trucks. The picture below shows the three locations.

In each of the three locations, there are 100 customers per day, and each customer buys a taco from the nearest vendor. If the two trucks are in the same location, then each vendor gets half of the customers. So, for example, if Miguel's truck is in location A, and Stephanie's is also in location A, then half of customers from locations A, B, and C will buy from Miguel's and the other half will buy from Stephanie's, so that each gets a profit of $150. If Miguel's truck is in location A and Stephanie's is in location B, then everyone in location A will buy from Miguel and everyone from locations B and C will buy from Stephanie, so that Miguel's profit is $100 while Stephanie's is $200. If Miguel's truck is in location A and Stephanie's is in location C, then everyone in A plus a half from B will buy from Miguel, and everyone in C plus half from B will buy from Stephanie so that each vendor gets a profit of $150, and so on. The table below is the payoff matrix for this game. The first number in each cell is Miguel's profit, and the second number is Stephanie's profit.

Refer to the scenario above.If Miguel's truck is located at B,what is Stephanie's best response?

A) Location A
B) Location B
C) Location C
D) Location A or B

Question 55

How does a dominant strategy equilibrium occur in a simultaneous-move game?

Question 56

The following payoff matrix represents a simultaneous-move game between two players: John and Trevor. Each player has to choices: Black or White. The first number in each cell is the payoff to John, and the second number is the payoff to Trevor.

Refer to the table above.Which statement is true?

A) John and Trevor both have a dominant strategy in this game.
B) Only John has a dominant strategy in this game.
C) Only Trevor has a dominant strategy in this game.
D) Neither John nor Trevor have a dominant strategy in this game.

Question 57

Scenario: Miguel and Stephanie are competitors who sell tacos out of their food trucks by the same beach. For each taco they sell, they get a profit of $1.00. Each morning they must decide at which of the three legally permitted locations, A, B, or C, they should park their trucks. The picture below shows the three locations.

In each of the three locations, there are 100 customers per day, and each customer buys a taco from the nearest vendor. If the two trucks are in the same location, then each vendor gets half of the customers. So, for example, if Miguel's truck is in location A, and Stephanie's is also in location A, then half of customers from locations A, B, and C will buy from Miguel's and the other half will buy from Stephanie's, so that each gets a profit of $150. If Miguel's truck is in location A and Stephanie's is in location B, then everyone in location A will buy from Miguel and everyone from locations B and C will buy from Stephanie, so that Miguel's profit is $100 while Stephanie's is $200. If Miguel's truck is in location A and Stephanie's is in location C, then everyone in A plus a half from B will buy from Miguel, and everyone in C plus half from B will buy from Stephanie so that each vendor gets a profit of $150, and so on. The table below is the payoff matrix for this game. The first number in each cell is Miguel's profit, and the second number is Stephanie's profit.

Refer to the scenario above.Does Miguel have a dominant strategy?

A) Yes, it is location A.
B) Yes, it is location B.
C) Yes, it is location C
D) No, he does not have a dominant strategy.

Question 58

The following figure depicts four simultaneous-move games. The first element of each payoff cell is the payoff to Player A, and the second element is the payoff to Player B.

Refer to the figure above.In which of these simultaneous-move games does only player A have a dominant strategy?

A) (1)
B) (2)
C) (3)
D) (4)

Question 59

Scenario: Miguel and Stephanie are competitors who sell tacos out of their food trucks by the same beach. For each taco they sell, they get a profit of $1.00. Each morning they must decide at which of the three legally permitted locations, A, B, or C, they should park their trucks. The picture below shows the three locations.

In each of the three locations, there are 100 customers per day, and each customer buys a taco from the nearest vendor. If the two trucks are in the same location, then each vendor gets half of the customers. So, for example, if Miguel's truck is in location A, and Stephanie's is also in location A, then half of customers from locations A, B, and C will buy from Miguel's and the other half will buy from Stephanie's, so that each gets a profit of $150. If Miguel's truck is in location A and Stephanie's is in location B, then everyone in location A will buy from Miguel and everyone from locations B and C will buy from Stephanie, so that Miguel's profit is $100 while Stephanie's is $200. If Miguel's truck is in location A and Stephanie's is in location C, then everyone in A plus a half from B will buy from Miguel, and everyone in C plus half from B will buy from Stephanie so that each vendor gets a profit of $150, and so on. The table below is the payoff matrix for this game. The first number in each cell is Miguel's profit, and the second number is Stephanie's profit.

Refer to the scenario above.Does Stephanie have a dominant strategy?

A) Yes, it is location A.
B) Yes, it is location B.
C) Yes, it is location C
D) No, she does not have a dominant strategy.

Question 60

Scenario: The payoff matrix given below shows the payoffs to two rival firms in millions of U.S. dollars for each strategy they choose. The first number listed in each cell is the payoff to the row player, and the second number listed is the payoff to the column player.

Refer to the scenario above.The sum of the firms' payoffs is maximum when ________.

A) both the firms choose Strategy X
B) both the firms choose Strategy Y
C) Firm A chooses Strategy X and Firm B chooses Strategy Y
D) Firm A chooses Strategy Y and Firm B chooses Strategy X

Question 61

The following payoff matrix represents a simultaneous-move game between two players: John and Trevor. Each player has to choices: Black or White. The first number in each cell is the payoff to John, and the second number is the payoff to Trevor.

Refer to the table above.What is the equilibrium of this game?

A) John and Trevor both choose Red.
B) John and Trevor both choose Yellow.
C) John chooses Red and Trevor chooses Yellow.
D) There is no dominant strategy equilibrium in this game.

Question 62

Which of the following is true of a Nash equilibrium?

A) A game can have only one Nash equilibrium.
B) No player can improve his payoff by changing his strategy in a Nash equilibrium.
C) A Nash equilibrium cannot occur if each player is aware of the strategies of other players.
D) A Nash equilibrium occurs if each player earns a zero payoff irrespective of the strategy he chooses.

Question 63

A Nash equilibrium occurs if each player chooses ________.

A) strategies that are mutual best responses
B) his or her dominant strategy
C) only a pure strategy
D) only a mixed strategy

Question 64

Scenario: The payoff matrix given below shows the payoffs to two firms in millions of U.S. dollars for choosing two alternative strategies. The first number listed in each cell is the payoff to the row player, and the second number listed is the payoff to the column player.

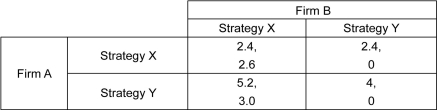
Refer to the scenario above.What is the payoff to Firm B in equilibrium?

A) $2.6 million
B) $0
C) $4 million
D) $3 million

Question 65

Scenario: The following payoff matrix represents a simultaneous-move game between two players: Kay and Jack. Each player has two choices: Black or White. The first number in each cell is the payoff to Kay, and the second number is the payoff to Jack.

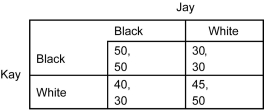
Refer to the scenario above.If Kay and Jay both choose White,________.

A) Kay will be better off if she switches to Black
B) Kay will be better off if she doesn't change her choice
C) Kay will get a payoff of $50
D) Jay will get a payoff of $30

Question 66

Scenario: Jack and Jill have gone cycling and have come to a place where the road is obstructed by a fallen tree. They can move the tree if both of them try. If neither of them tries, they have to turn back and reach home very late. However, if one of them tries while the other does not help, the one who tries will have a muscle sprain and will not be able to move the tree. The matrix below shows the utility each player derives in each situation. The first number listed in each cell is the payoff to the row player, and the second number listed is the payoff to the column player.

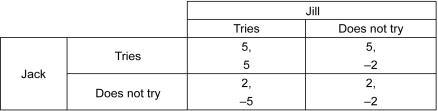
Refer to the scenario above.This game ________.

A) has a unique Nash equilibrium
B) has a unique dominant strategy equilibrium
C) does not have a dominant strategy equilibrium
D) does not have a Nash equilibrium

Question 67

Scenario: The payoff matrix given below shows the payoffs to two firms in millions of U.S. dollars for choosing two alternative strategies. The first number listed in each cell is the payoff to the row player, and the second number listed is the payoff to the column player.

Refer to the scenario above.Which of the following is true in this case?

A) This game has multiple Nash equilibria.
B) This game does not have a Nash equilibrium.
C) The dominant strategy equilibrium of this game is also its Nash equilibrium.
D) The dominant strategy equilibrium of this game is not Pareto efficient.

Question 68

Scenario: Jack and Jill have gone cycling and have come to a place where the road is obstructed by a fallen tree. They can move the tree if both of them try. If neither of them tries, they have to turn back and reach home very late. However, if one of them tries while the other does not help, the one who tries will have a muscle sprain and will not be able to move the tree. The matrix below shows the utility each player derives in each situation. The first number listed in each cell is the payoff to the row player, and the second number listed is the payoff to the column player.

Refer to the scenario above.Jack will derive ________ units of utility if Jill tries to move the tree while he does not try at all.

A) 5
B) −5
C) 2
D) 10

Question 69

Scenario: The payoff matrix given below shows the payoffs to two firms in millions of U.S. dollars for choosing two alternative strategies. The first number listed in each cell is the payoff to the row player, and the second number listed is the payoff to the column player.

Refer to the scenario above.Which of the following will happen in equilibrium?

A) Firm A will choose Strategy X, and Firm B will choose Strategy Y.
B) Firm A will choose Strategy Y, and Firm B will choose Strategy X.
C) Both the firms will choose Strategy X.
D) Both the firms will choose Strategy Y.

Question 70

Scenario: Jack and Jill have gone cycling and have come to a place where the road is obstructed by a fallen tree. They can move the tree if both of them try. If neither of them tries, they have to turn back and reach home very late. However, if one of them tries while the other does not help, the one who tries will have a muscle sprain and will not be able to move the tree. The matrix below shows the utility each player derives in each situation. The first number listed in each cell is the payoff to the row player, and the second number listed is the payoff to the column player.

Refer to the scenario above.This is an example of a(n)________.

A) simultaneous-move game
B) extensive-form game
C) mixed-strategy game
D) symmetric game

Question 71

Scenario: Jack and Jill have gone cycling and have come to a place where the road is obstructed by a fallen tree. They can move the tree if both of them try. If neither of them tries, they have to turn back and reach home very late. However, if one of them tries while the other does not help, the one who tries will have a muscle sprain and will not be able to move the tree. The matrix below shows the utility each player derives in each situation. The first number listed in each cell is the payoff to the row player, and the second number listed is the payoff to the column player.

Refer to the scenario above.Jack will derive ________ units of utility if he tries to move the tree while Jill does not try at all.

A) 5
B) −5
C) −2
D) 10

Question 72

Consider another version of the advertising game between Mountain Dew and Mello Yello.Again,each brand is deciding whether to launch an advertising campaign.These decisions will be taken simultaneously,the brands will not be cooperating,and we will assume each brand's strategist knows her own and her opponent's payoffs in all cases.The payoff matrix is listed below.

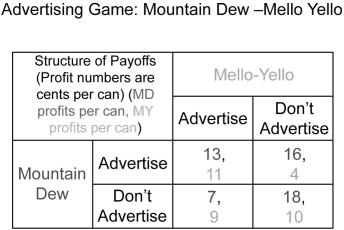
Is there a Nash equilibrium in this advertising game?

A) Yes, Mountain Dew chooses to not advertise, Mello Yello chooses to advertise
B) Yes, both Mountain Dew and Mello Yello choose to advertise
C) Yes, both Mountain Dew and Mello Yello choose to not advertise
D) Yes, both (B and C)

Question 73

Scenario: Jack and Jill have gone cycling and have come to a place where the road is obstructed by a fallen tree. They can move the tree if both of them try. If neither of them tries, they have to turn back and reach home very late. However, if one of them tries while the other does not help, the one who tries will have a muscle sprain and will not be able to move the tree. The matrix below shows the utility each player derives in each situation. The first number listed in each cell is the payoff to the row player, and the second number listed is the payoff to the column player.

Refer to the scenario above.Jack and Jill will derive maximum utility if ________.

A) Jack tries to move the tree while Jill does not
B) Jill tries to move the tree while jack does not
C) both of them try to move the tree
D) neither of them tries to move the tree

Question 74

Scenario: Jack and Jill have gone cycling and have come to a place where the road is obstructed by a fallen tree. They can move the tree if both of them try. If neither of them tries, they have to turn back and reach home very late. However, if one of them tries while the other does not help, the one who tries will have a muscle sprain and will not be able to move the tree. The matrix below shows the utility each player derives in each situation. The first number listed in each cell is the payoff to the row player, and the second number listed is the payoff to the column player.

Refer to the scenario above.Jill will derive ________ units of utility if she tries to move the tree while Jack does not try at all.

A) 5
B) −5
C) −2
D) 10

Question 75

Scenario: The payoff matrix given below shows the payoffs to two firms in millions of U.S. dollars for choosing two alternative strategies. The first number listed in each cell is the payoff to the row player, and the second number listed is the payoff to the column player.

Refer to the scenario above.What is the payoff to Firm A in equilibrium?

A) $2.4 million
B) $2.6 million
C) $5.2 million
D) $3.0 million

Question 76

Scenario: Jack and Jill have gone cycling and have come to a place where the road is obstructed by a fallen tree. They can move the tree if both of them try. If neither of them tries, they have to turn back and reach home very late. However, if one of them tries while the other does not help, the one who tries will have a muscle sprain and will not be able to move the tree. The matrix below shows the utility each player derives in each situation. The first number listed in each cell is the payoff to the row player, and the second number listed is the payoff to the column player.

Refer to the scenario above.Jack will derive ________ units of utility if Jill tries to move the tree while he does not try at all.

A) 5
B) -5
C) 2
D) 10

Question 77

In a game,a Nash equilibrium is reached only if the players ________.

A) understand the game and the payoffs associated with each strategy
B) follow a mixed strategy
C) use backward induction to develop their strategies
D) have no best response for the choices made by other players

Question 78

Scenario: Jack and Jill have gone cycling and have come to a place where the road is obstructed by a fallen tree. They can move the tree if both of them try. If neither of them tries, they have to turn back and reach home very late. However, if one of them tries while the other does not help, the one who tries will have a muscle sprain and will not be able to move the tree. The matrix below shows the utility each player derives in each situation. The first number listed in each cell is the payoff to the row player, and the second number listed is the payoff to the column player.

Refer to the scenario above.Which of the following is true in this case?

A) Jack is better off not trying to move the tree if Jill does not try at all.
B) Jill is better off trying to move the tree if Jack does not try at all.
C) Jack is better off trying to move the tree regardless of what Jill does.
D) Jill is better off not trying if Jack tries to move the tree.

Question 79

Scenario: The following payoff matrix represents a simultaneous-move game between two players: Kay and Jack. Each player has two choices: Black or White. The first number in each cell is the payoff to Kay, and the second number is the payoff to Jack.

Refer to the scenario above.Which is true?

A) This game has one Nash equilibrium.
B) This game has two Nash equilibria.
C) This game has a dominant strategy equilibrium.
D) This game has two dominant strategy equilibria.

Question 80

Scenario: The following payoff matrix represents a simultaneous-move game between two players: Dan and Jessa. Each player has two choices: Strategy X or Strategy Y. The first number in each cell is the payoff to Dan, and the second number is the payoff to Jessa.

Refer to the scenario above.Which statement is true?

A) Dan's dominant strategy is Y.
B) Jessa's dominant strategy is X.
C) Dan does not have a dominant strategy.
D) Dan will choose Y only when Jessa chooses Y.