Deck 18: Model Building
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/148
Play
Full screen (f)
Deck 18: Model Building
1
Suppose that the sample regression equation of a model is 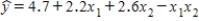 .If we examine the relationship between y and x2 for x1 = 1,2,and 3,we observe that the three equations produced not only differ in the intercept term,but the coefficient of x2 also varies.
.If we examine the relationship between y and x2 for x1 = 1,2,and 3,we observe that the three equations produced not only differ in the intercept term,but the coefficient of x2 also varies.
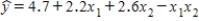 .If we examine the relationship between y and x2 for x1 = 1,2,and 3,we observe that the three equations produced not only differ in the intercept term,but the coefficient of x2 also varies.
.If we examine the relationship between y and x2 for x1 = 1,2,and 3,we observe that the three equations produced not only differ in the intercept term,but the coefficient of x2 also varies.True
2
In the first-order regression model 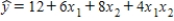 ,a unit increase in x1 increases the value of y on average by 6 units.
,a unit increase in x1 increases the value of y on average by 6 units.
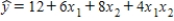 ,a unit increase in x1 increases the value of y on average by 6 units.
,a unit increase in x1 increases the value of y on average by 6 units.False
3
In the first-order model 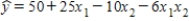 ,a unit increase in x2,while holding x1 constant at a value of 3,decreases the value of y on average by 3 units.
,a unit increase in x2,while holding x1 constant at a value of 3,decreases the value of y on average by 3 units.
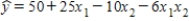 ,a unit increase in x2,while holding x1 constant at a value of 3,decreases the value of y on average by 3 units.
,a unit increase in x2,while holding x1 constant at a value of 3,decreases the value of y on average by 3 units.False
4
The model 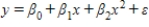 is referred to as a simple linear regression model.
is referred to as a simple linear regression model.
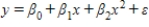 is referred to as a simple linear regression model.
is referred to as a simple linear regression model.
Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
5
Which of the following is not an advantage of multiple regression as compared with analysis of variance?
A)Multiple regression can be used to estimate the relationship between the dependent variable and independent variables.
B)Multiple regression handles problems with more than two independent variables easier than analysis of variance.
C)Multiple regression handles nominal variables better than analysis of variance.
D)All of these choices are true are advantages of multiple regression as compared with analysis of variance.
A)Multiple regression can be used to estimate the relationship between the dependent variable and independent variables.
B)Multiple regression handles problems with more than two independent variables easier than analysis of variance.
C)Multiple regression handles nominal variables better than analysis of variance.
D)All of these choices are true are advantages of multiple regression as compared with analysis of variance.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
6
The model y = β0 + β1x1 + β2x2 + ε is referred to as a first-order model with two predictor variables with no interaction.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
7
The model 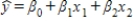 is used whenever the statistician believes that,on average,y is linearly related to x1 and x2 and the predictor variables do not interact.
is used whenever the statistician believes that,on average,y is linearly related to x1 and x2 and the predictor variables do not interact.
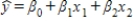 is used whenever the statistician believes that,on average,y is linearly related to x1 and x2 and the predictor variables do not interact.
is used whenever the statistician believes that,on average,y is linearly related to x1 and x2 and the predictor variables do not interact.
Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
8
Regression analysis allows the statistics practitioner to use mathematical models to realistically describe relationships between the dependent variable and independent variables.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
9
The graph of the model 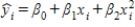 is shaped like a straight line going upwards.
is shaped like a straight line going upwards.
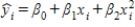 is shaped like a straight line going upwards.
is shaped like a straight line going upwards.
Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
10
Suppose that the sample regression equation of a model is 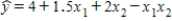 .If we examine the relationship between x1 and y for four different values of x2,we observe that the four equations produced differ only in the intercept term.
.If we examine the relationship between x1 and y for four different values of x2,we observe that the four equations produced differ only in the intercept term.
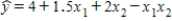 .If we examine the relationship between x1 and y for four different values of x2,we observe that the four equations produced differ only in the intercept term.
.If we examine the relationship between x1 and y for four different values of x2,we observe that the four equations produced differ only in the intercept term.
Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
11
In a first-order model with two predictors x1 and x2,an interaction term may be used when the relationship between the dependent variable y and the predictor variables is linear.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
12
A first-order polynomial model with one predictor variable is the familiar simple linear regression model.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
13
In the first-order model 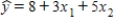 ,a unit increase in x2,while holding x1 constant,increases the value of y on average by 5 units.
,a unit increase in x2,while holding x1 constant,increases the value of y on average by 5 units.
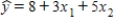 ,a unit increase in x2,while holding x1 constant,increases the value of y on average by 5 units.
,a unit increase in x2,while holding x1 constant,increases the value of y on average by 5 units.
Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
14
We interpret the coefficients in a multiple regression model by holding all variables in the model constant.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
15
In the first-order model 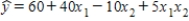 ,a unit increase in x2,while holding x1 constant at 1,changes the value of y on average by −5 units.
,a unit increase in x2,while holding x1 constant at 1,changes the value of y on average by −5 units.
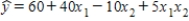 ,a unit increase in x2,while holding x1 constant at 1,changes the value of y on average by −5 units.
,a unit increase in x2,while holding x1 constant at 1,changes the value of y on average by −5 units.
Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
16
The model 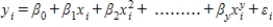 is referred to as a polynomial model with one predictor variable.
is referred to as a polynomial model with one predictor variable.
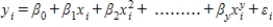 is referred to as a polynomial model with one predictor variable.
is referred to as a polynomial model with one predictor variable.
Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
17
The model y = β0 + β1x1 + β2x2 + β3x1x2 + ε is referred to as a second-order model with two predictor variables with interaction.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
18
In a first-order model with two predictors x1 and x2,an interaction term may be used when the:
A)relationship between the dependent variable and the independent variables is linear.
B)effect of x1 on the dependent variable is influenced by x2.
C)Effect of x2 on the dependent variable is influenced by x1.
D) both b and c.
A)relationship between the dependent variable and the independent variables is linear.
B)effect of x1 on the dependent variable is influenced by x2.
C)Effect of x2 on the dependent variable is influenced by x1.
D) both b and c.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
19
Suppose that the sample regression line of the first-order model is 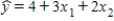 .If we examine the relationship between y and x1 for three different values of x2,we observe that the effect of x1 on y remains the same no matter what the value of x2.
.If we examine the relationship between y and x1 for three different values of x2,we observe that the effect of x1 on y remains the same no matter what the value of x2.
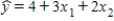 .If we examine the relationship between y and x1 for three different values of x2,we observe that the effect of x1 on y remains the same no matter what the value of x2.
.If we examine the relationship between y and x1 for three different values of x2,we observe that the effect of x1 on y remains the same no matter what the value of x2.
Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
20
In the first-order model 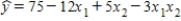 ,a unit increase in x1,while holding x2 constant at a value of 2,decreases the value of y on average by 8 units.
,a unit increase in x1,while holding x2 constant at a value of 2,decreases the value of y on average by 8 units.
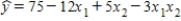 ,a unit increase in x1,while holding x2 constant at a value of 2,decreases the value of y on average by 8 units.
,a unit increase in x1,while holding x2 constant at a value of 2,decreases the value of y on average by 8 units.
Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
21
When we plot x versus y,the graph of the model y = β0 + β1x + β2x2 + ε is shaped like a:
A)straight line going upwards.
B)circle.
C)parabola.
D)None of these choices.
A)straight line going upwards.
B)circle.
C)parabola.
D)None of these choices.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
22
The model y = β0 + β1x1 + β2x2 + β3x1x2 + ε is referred to as a:
A)first-order model with two predictor variables with no interaction.
B)first-order model with two predictor variables with interaction.
C)second-order model with three predictor variables with no interaction.
D)second-order model with three predictor variables with interaction.
A)first-order model with two predictor variables with no interaction.
B)first-order model with two predictor variables with interaction.
C)second-order model with three predictor variables with no interaction.
D)second-order model with three predictor variables with interaction.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
23
The model y = β0 + β1x1 + β2x2 + ε is used whenever the statistician believes that,on average,y is linearly related to:
A)x1 and the predictor variables do not interact.
B) x2 and the predictor variables do not interact.
C) Both a and b.
D) None of these choices.
A)x1 and the predictor variables do not interact.
B) x2 and the predictor variables do not interact.
C) Both a and b.
D) None of these choices.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
24
Suppose that the sample regression equation of a second-order model is given by 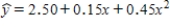 .Then,the value 4.60 is the:
.Then,the value 4.60 is the:
A)predicted value of y for any positive value of x.
B)predicted value of y when x = 2.
C)estimated change in y when x increases by 1 unit .
D)intercept where the response surface strikes the x-axis.
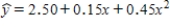 .Then,the value 4.60 is the:
.Then,the value 4.60 is the:A)predicted value of y for any positive value of x.
B)predicted value of y when x = 2.
C)estimated change in y when x increases by 1 unit .
D)intercept where the response surface strikes the x-axis.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
25
The independent variable x in a polynomial model is called the ____________________ variable.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
26
The model y = β0 + β1x + β2x2 + ε is referred to as a:
A)simple linear regression model.
B)first-order model with one predictor variable.
C)second-order model with one predictor variable.
D)third order model with two predictor variables.
A)simple linear regression model.
B)first-order model with one predictor variable.
C)second-order model with one predictor variable.
D)third order model with two predictor variables.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
27
Suppose that the sample regression equation of a second-order model is given by 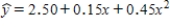 .Then,the value 2.50 is the:
.Then,the value 2.50 is the:
A)intercept where the response surface strikes the y-axis.
B)intercept where the response surface strikes the x-axis.
C)predicted value of y.
D)None of these choices.
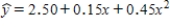 .Then,the value 2.50 is the:
.Then,the value 2.50 is the:A)intercept where the response surface strikes the y-axis.
B)intercept where the response surface strikes the x-axis.
C)predicted value of y.
D)None of these choices.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
28
For the following regression equation 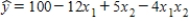 ,a unit increase in x1,while holding x2 constant at a value of 2,decreases the value of y on average by:
,a unit increase in x1,while holding x2 constant at a value of 2,decreases the value of y on average by:
A)92
B)85
C)20
D)an amount that depends on the value of x1.
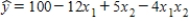 ,a unit increase in x1,while holding x2 constant at a value of 2,decreases the value of y on average by:
,a unit increase in x1,while holding x2 constant at a value of 2,decreases the value of y on average by:A)92
B)85
C)20
D)an amount that depends on the value of x1.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
29
The model y = β0 + β1x + β2x2 +.........+ βpxp + ε is referred to as a polynomial model with:
A)one predictor variable.
B)p predictor variables.
C)(p + 1)predictor variables.
D)x predictor variables.
A)one predictor variable.
B)p predictor variables.
C)(p + 1)predictor variables.
D)x predictor variables.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
30
For the following regression equation 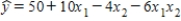 ,a unit increase in x2,while holding x1 constant at a value of 3,decreases the value of y on average by:
,a unit increase in x2,while holding x1 constant at a value of 3,decreases the value of y on average by:
A)22
B)50
C)56
D)An amount that depends on the value of x2
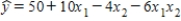 ,a unit increase in x2,while holding x1 constant at a value of 3,decreases the value of y on average by:
,a unit increase in x2,while holding x1 constant at a value of 3,decreases the value of y on average by:A)22
B)50
C)56
D)An amount that depends on the value of x2

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
31
The model y = β0 + β1x1 + β2x2 + ε is referred to as a:
A)first-order model with one predictor variable.
B)first-order model with two predictor variables.
C)second-order model with one predictor variable.
D)second-order model with two predictor variables.
A)first-order model with one predictor variable.
B)first-order model with two predictor variables.
C)second-order model with one predictor variable.
D)second-order model with two predictor variables.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
32
For the following regression equation 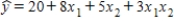 ,which combination of x1 and x2,respectively,results in the largest average value of y?
,which combination of x1 and x2,respectively,results in the largest average value of y?
A)3 and 5
B)5 and 3
C)6 and 3
D)3 and 6
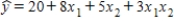 ,which combination of x1 and x2,respectively,results in the largest average value of y?
,which combination of x1 and x2,respectively,results in the largest average value of y?A)3 and 5
B)5 and 3
C)6 and 3
D)3 and 6

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
33
For the following regression equation 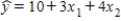 ,a unit increase in x2 increases the value of y on average by:
,a unit increase in x2 increases the value of y on average by:
A)4
B)7
C)17
D)an amount that depends on the value of x1.
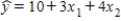 ,a unit increase in x2 increases the value of y on average by:
,a unit increase in x2 increases the value of y on average by:A)4
B)7
C)17
D)an amount that depends on the value of x1.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
34
For the following regression equation 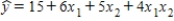 ,a unit increase in x1 increases the value of y on average by:
,a unit increase in x1 increases the value of y on average by:
A)5
B)30
C)26
D)an amount that depends on the value of x2
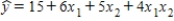 ,a unit increase in x1 increases the value of y on average by:
,a unit increase in x1 increases the value of y on average by:A)5
B)30
C)26
D)an amount that depends on the value of x2

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
35
For the following regression equation 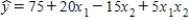 ,a unit increase in x2,while holding x1 constant at 1,changes the value of y on average by:
,a unit increase in x2,while holding x1 constant at 1,changes the value of y on average by:
A)−5
B)+5
C)10
D)−10
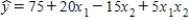 ,a unit increase in x2,while holding x1 constant at 1,changes the value of y on average by:
,a unit increase in x2,while holding x1 constant at 1,changes the value of y on average by:A)−5
B)+5
C)10
D)−10

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
36
Which of the following statements is false regarding the graph of the second-order polynomial model y = β0 + β1x + β2x2 + ε?
A)If β2 is negative,the graph is concave,while if β2 is positive,the graph is convex.
B)The greater the absolute value of β2,the smaller the rate of curvature.
C)When we plot x versus y,the graph is shaped like a parabola.
D)All of these choices are true.
A)If β2 is negative,the graph is concave,while if β2 is positive,the graph is convex.
B)The greater the absolute value of β2,the smaller the rate of curvature.
C)When we plot x versus y,the graph is shaped like a parabola.
D)All of these choices are true.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
37
Suppose that the sample regression line of the first-order model is 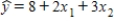 .If we examine the relationship between y and x1 for four different values of x2,we observe that the:
.If we examine the relationship between y and x1 for four different values of x2,we observe that the:
A)only difference in the four equations produced is the coefficient of x2.
B)effect of x1 on y remains the same no matter what the value of x2.
C)effect of x1 on y remains the same no matter what the value of x1.
D)Cannot answer this question without more information.
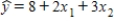 .If we examine the relationship between y and x1 for four different values of x2,we observe that the:
.If we examine the relationship between y and x1 for four different values of x2,we observe that the:A)only difference in the four equations produced is the coefficient of x2.
B)effect of x1 on y remains the same no matter what the value of x2.
C)effect of x1 on y remains the same no matter what the value of x1.
D)Cannot answer this question without more information.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
38
Another term for a first-order polynomial model is a regression ____________________.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
39
A second-order polynomial model is shaped like a(n)____________________.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
40
Suppose that the sample regression equation of a model is 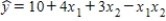 .If we examine the relationship between x1 and y for three different values of x2,we observe that the:
.If we examine the relationship between x1 and y for three different values of x2,we observe that the:
A)three equations produced differ not only in the intercept term but also the coefficient of x1 varies.
B)coefficient of x2 remains unchanged.
C)coefficient of x1 varies.
D)three equations produced differ only in the intercept.
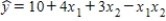 .If we examine the relationship between x1 and y for three different values of x2,we observe that the:
.If we examine the relationship between x1 and y for three different values of x2,we observe that the:A)three equations produced differ not only in the intercept term but also the coefficient of x1 varies.
B)coefficient of x2 remains unchanged.
C)coefficient of x1 varies.
D)three equations produced differ only in the intercept.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
41
The model y = β0 + β1x1 + β2x2 + β3x1x2 + ε is a(n)____________________-order polynomial model with ____________________ predictor variables and ____________________.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
42
____________________ means that the effect of x1 on y is influenced by the value of x2,and vice versa.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
43
Computer Training
Consider the following data for two variables,x and y.The independent variable x represents the amount of training time (in hours)for a salesperson starting in a new computer store to adjust fully,and the dependent variable y represents the weekly sales (in $1000s). Use statistical software to answer the following question(s).
Use statistical software to answer the following question(s).
{Computer Training Narrative} Estimate the value of y when x = 45 using the estimated linear regression equation in the previous question.
Consider the following data for two variables,x and y.The independent variable x represents the amount of training time (in hours)for a salesperson starting in a new computer store to adjust fully,and the dependent variable y represents the weekly sales (in $1000s).
 Use statistical software to answer the following question(s).
Use statistical software to answer the following question(s). {Computer Training Narrative} Estimate the value of y when x = 45 using the estimated linear regression equation in the previous question.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
44
The model y = β0 + β1x1 + β2x2 + ε is a(n)____________________-order polynomial model with ____________________ predictor variable(s).

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
45
In a first-order polynomial model with no interaction,the effect of x1 on y remains the same no matter what the value of x2 is.The graph of this model produces straight lines that are ____________________ to each other.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
46
Computer Training
Consider the following data for two variables,x and y.The independent variable x represents the amount of training time (in hours)for a salesperson starting in a new computer store to adjust fully,and the dependent variable y represents the weekly sales (in $1000s). Use statistical software to answer the following question(s).
Use statistical software to answer the following question(s).
{Computer Training Narrative} Find the coefficient of determination of this simple linear model.What does this statistic tell you about the model?
Consider the following data for two variables,x and y.The independent variable x represents the amount of training time (in hours)for a salesperson starting in a new computer store to adjust fully,and the dependent variable y represents the weekly sales (in $1000s).
 Use statistical software to answer the following question(s).
Use statistical software to answer the following question(s). {Computer Training Narrative} Find the coefficient of determination of this simple linear model.What does this statistic tell you about the model?

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
47
Computer Training
Consider the following data for two variables,x and y.The independent variable x represents the amount of training time (in hours)for a salesperson starting in a new computer store to adjust fully,and the dependent variable y represents the weekly sales (in $1000s). Use statistical software to answer the following question(s).
Use statistical software to answer the following question(s).
{Computer Training Narrative} Use the quadratic model to predict the value of y when x = 45.
Consider the following data for two variables,x and y.The independent variable x represents the amount of training time (in hours)for a salesperson starting in a new computer store to adjust fully,and the dependent variable y represents the weekly sales (in $1000s).
 Use statistical software to answer the following question(s).
Use statistical software to answer the following question(s). {Computer Training Narrative} Use the quadratic model to predict the value of y when x = 45.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
48
Hockey Teams
An avid hockey fan was in the process of examining the factors that determine the success or failure of hockey teams.He noticed that teams with many rookies and teams with many veterans seem to do quite poorly.To further analyze his beliefs he took a random sample of 20 teams and proposed a second-order model with one independent variable,average years of professional experience.The selected model is y = β0 + β1x + β2x2 + ε,where y = winning team's percentage,and x = average years of professional experience.The computer output is shown below. THE REGRESSION EQUATION IS y = 32.6 + 5.96x− .48x2 S = 16.1 R−Sq = 43.9% ANALYSIS OF VARIANCE
S = 16.1 R−Sq = 43.9% ANALYSIS OF VARIANCE 
{Hockey Teams Narrative} Predict the winning percentage for a hockey team with an average of 6 years of professional experience.
An avid hockey fan was in the process of examining the factors that determine the success or failure of hockey teams.He noticed that teams with many rookies and teams with many veterans seem to do quite poorly.To further analyze his beliefs he took a random sample of 20 teams and proposed a second-order model with one independent variable,average years of professional experience.The selected model is y = β0 + β1x + β2x2 + ε,where y = winning team's percentage,and x = average years of professional experience.The computer output is shown below. THE REGRESSION EQUATION IS y = 32.6 + 5.96x− .48x2
 S = 16.1 R−Sq = 43.9% ANALYSIS OF VARIANCE
S = 16.1 R−Sq = 43.9% ANALYSIS OF VARIANCE 
{Hockey Teams Narrative} Predict the winning percentage for a hockey team with an average of 6 years of professional experience.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
49
Motorcycle Fatalities
A traffic consultant has analyzed the factors that affect the number of motorcycle fatalities.She has come to the conclusion that two important variables are the number of motorcycle and the number of cars.She proposed the model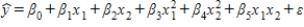 (the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS
(the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS 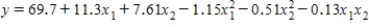
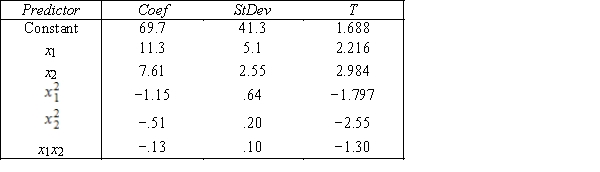 S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE
S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE 
{Motorcycle Fatalities Narrative} Is there enough evidence at the 5% significance level to conclude that the model is useful in predicting the number of fatalities?
A traffic consultant has analyzed the factors that affect the number of motorcycle fatalities.She has come to the conclusion that two important variables are the number of motorcycle and the number of cars.She proposed the model
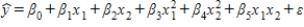 (the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS
(the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS 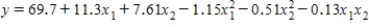
 S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE
S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE 
{Motorcycle Fatalities Narrative} Is there enough evidence at the 5% significance level to conclude that the model is useful in predicting the number of fatalities?

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
50
If a quadratic relationship exists between y and each of x1 and x2,you use a(n)____________________-order polynomial model.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
51
Computer Training
Consider the following data for two variables,x and y.The independent variable x represents the amount of training time (in hours)for a salesperson starting in a new computer store to adjust fully,and the dependent variable y represents the weekly sales (in $1000s). Use statistical software to answer the following question(s).
Use statistical software to answer the following question(s).
{Computer Training Narrative} Develop a scatter diagram for the data.Does the scatter diagram suggest an estimated regression equation of the form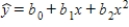 ? Explain.
? Explain.
Consider the following data for two variables,x and y.The independent variable x represents the amount of training time (in hours)for a salesperson starting in a new computer store to adjust fully,and the dependent variable y represents the weekly sales (in $1000s).
 Use statistical software to answer the following question(s).
Use statistical software to answer the following question(s). {Computer Training Narrative} Develop a scatter diagram for the data.Does the scatter diagram suggest an estimated regression equation of the form
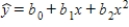 ? Explain.
? Explain.
Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
52
Computer Training
Consider the following data for two variables,x and y.The independent variable x represents the amount of training time (in hours)for a salesperson starting in a new computer store to adjust fully,and the dependent variable y represents the weekly sales (in $1000s). Use statistical software to answer the following question(s).
Use statistical software to answer the following question(s).
{Computer Training Narrative} Develop an estimated regression equation of the form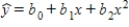 .
.
Consider the following data for two variables,x and y.The independent variable x represents the amount of training time (in hours)for a salesperson starting in a new computer store to adjust fully,and the dependent variable y represents the weekly sales (in $1000s).
 Use statistical software to answer the following question(s).
Use statistical software to answer the following question(s). {Computer Training Narrative} Develop an estimated regression equation of the form
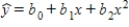 .
.
Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
53
Computer Training
Consider the following data for two variables,x and y.The independent variable x represents the amount of training time (in hours)for a salesperson starting in a new computer store to adjust fully,and the dependent variable y represents the weekly sales (in $1000s). Use statistical software to answer the following question(s).
Use statistical software to answer the following question(s).
{Computer Training Narrative} Determine the coefficient of determination quadratic model.What does this statistic tell you about this model?
Consider the following data for two variables,x and y.The independent variable x represents the amount of training time (in hours)for a salesperson starting in a new computer store to adjust fully,and the dependent variable y represents the weekly sales (in $1000s).
 Use statistical software to answer the following question(s).
Use statistical software to answer the following question(s). {Computer Training Narrative} Determine the coefficient of determination quadratic model.What does this statistic tell you about this model?

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
54
Computer Training
Consider the following data for two variables,x and y.The independent variable x represents the amount of training time (in hours)for a salesperson starting in a new computer store to adjust fully,and the dependent variable y represents the weekly sales (in $1000s). Use statistical software to answer the following question(s).
Use statistical software to answer the following question(s).
{Computer Training Narrative} Determine if there is sufficient evidence at the 5% significance level to infer that the quadratic relationship between y,x,and x2 in the previous question is significant.
Consider the following data for two variables,x and y.The independent variable x represents the amount of training time (in hours)for a salesperson starting in a new computer store to adjust fully,and the dependent variable y represents the weekly sales (in $1000s).
 Use statistical software to answer the following question(s).
Use statistical software to answer the following question(s). {Computer Training Narrative} Determine if there is sufficient evidence at the 5% significance level to infer that the quadratic relationship between y,x,and x2 in the previous question is significant.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
55
Computer Training
Consider the following data for two variables,x and y.The independent variable x represents the amount of training time (in hours)for a salesperson starting in a new computer store to adjust fully,and the dependent variable y represents the weekly sales (in $1000s). Use statistical software to answer the following question(s).
Use statistical software to answer the following question(s).
{Computer Training Narrative} Determine if there is sufficient evidence at the 5% significance level to infer that the relationship between x and y is positive and significant.
Consider the following data for two variables,x and y.The independent variable x represents the amount of training time (in hours)for a salesperson starting in a new computer store to adjust fully,and the dependent variable y represents the weekly sales (in $1000s).
 Use statistical software to answer the following question(s).
Use statistical software to answer the following question(s). {Computer Training Narrative} Determine if there is sufficient evidence at the 5% significance level to infer that the relationship between x and y is positive and significant.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
56
Hockey Teams
An avid hockey fan was in the process of examining the factors that determine the success or failure of hockey teams.He noticed that teams with many rookies and teams with many veterans seem to do quite poorly.To further analyze his beliefs he took a random sample of 20 teams and proposed a second-order model with one independent variable,average years of professional experience.The selected model is y = β0 + β1x + β2x2 + ε,where y = winning team's percentage,and x = average years of professional experience.The computer output is shown below. THE REGRESSION EQUATION IS y = 32.6 + 5.96x− .48x2 S = 16.1 R−Sq = 43.9% ANALYSIS OF VARIANCE
S = 16.1 R−Sq = 43.9% ANALYSIS OF VARIANCE 
{Hockey Teams Narrative} Test to determine at the 10% significance level if the linear term should be retained.
An avid hockey fan was in the process of examining the factors that determine the success or failure of hockey teams.He noticed that teams with many rookies and teams with many veterans seem to do quite poorly.To further analyze his beliefs he took a random sample of 20 teams and proposed a second-order model with one independent variable,average years of professional experience.The selected model is y = β0 + β1x + β2x2 + ε,where y = winning team's percentage,and x = average years of professional experience.The computer output is shown below. THE REGRESSION EQUATION IS y = 32.6 + 5.96x− .48x2
 S = 16.1 R−Sq = 43.9% ANALYSIS OF VARIANCE
S = 16.1 R−Sq = 43.9% ANALYSIS OF VARIANCE 
{Hockey Teams Narrative} Test to determine at the 10% significance level if the linear term should be retained.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
57
Hockey Teams
An avid hockey fan was in the process of examining the factors that determine the success or failure of hockey teams.He noticed that teams with many rookies and teams with many veterans seem to do quite poorly.To further analyze his beliefs he took a random sample of 20 teams and proposed a second-order model with one independent variable,average years of professional experience.The selected model is y = β0 + β1x + β2x2 + ε,where y = winning team's percentage,and x = average years of professional experience.The computer output is shown below. THE REGRESSION EQUATION IS y = 32.6 + 5.96x− .48x2 S = 16.1 R−Sq = 43.9% ANALYSIS OF VARIANCE
S = 16.1 R−Sq = 43.9% ANALYSIS OF VARIANCE 
{Hockey Teams Narrative} Do these results allow us to conclude at the 5% significance level that the model is useful in predicting the team's winning percentage?
An avid hockey fan was in the process of examining the factors that determine the success or failure of hockey teams.He noticed that teams with many rookies and teams with many veterans seem to do quite poorly.To further analyze his beliefs he took a random sample of 20 teams and proposed a second-order model with one independent variable,average years of professional experience.The selected model is y = β0 + β1x + β2x2 + ε,where y = winning team's percentage,and x = average years of professional experience.The computer output is shown below. THE REGRESSION EQUATION IS y = 32.6 + 5.96x− .48x2
 S = 16.1 R−Sq = 43.9% ANALYSIS OF VARIANCE
S = 16.1 R−Sq = 43.9% ANALYSIS OF VARIANCE 
{Hockey Teams Narrative} Do these results allow us to conclude at the 5% significance level that the model is useful in predicting the team's winning percentage?

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
58
Hockey Teams
An avid hockey fan was in the process of examining the factors that determine the success or failure of hockey teams.He noticed that teams with many rookies and teams with many veterans seem to do quite poorly.To further analyze his beliefs he took a random sample of 20 teams and proposed a second-order model with one independent variable,average years of professional experience.The selected model is y = β0 + β1x + β2x2 + ε,where y = winning team's percentage,and x = average years of professional experience.The computer output is shown below. THE REGRESSION EQUATION IS y = 32.6 + 5.96x− .48x2 S = 16.1 R−Sq = 43.9% ANALYSIS OF VARIANCE
S = 16.1 R−Sq = 43.9% ANALYSIS OF VARIANCE 
{Hockey Teams Narrative} What is the coefficient of determination? Explain what this statistic tells you about the model.
An avid hockey fan was in the process of examining the factors that determine the success or failure of hockey teams.He noticed that teams with many rookies and teams with many veterans seem to do quite poorly.To further analyze his beliefs he took a random sample of 20 teams and proposed a second-order model with one independent variable,average years of professional experience.The selected model is y = β0 + β1x + β2x2 + ε,where y = winning team's percentage,and x = average years of professional experience.The computer output is shown below. THE REGRESSION EQUATION IS y = 32.6 + 5.96x− .48x2
 S = 16.1 R−Sq = 43.9% ANALYSIS OF VARIANCE
S = 16.1 R−Sq = 43.9% ANALYSIS OF VARIANCE 
{Hockey Teams Narrative} What is the coefficient of determination? Explain what this statistic tells you about the model.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
59
Computer Training
Consider the following data for two variables,x and y.The independent variable x represents the amount of training time (in hours)for a salesperson starting in a new computer store to adjust fully,and the dependent variable y represents the weekly sales (in $1000s). Use statistical software to answer the following question(s).
Use statistical software to answer the following question(s).
{Computer Training Narrative} Develop an estimated regression equation of the form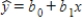 .
.
Consider the following data for two variables,x and y.The independent variable x represents the amount of training time (in hours)for a salesperson starting in a new computer store to adjust fully,and the dependent variable y represents the weekly sales (in $1000s).
 Use statistical software to answer the following question(s).
Use statistical software to answer the following question(s). {Computer Training Narrative} Develop an estimated regression equation of the form
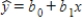 .
.
Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
60
Hockey Teams
An avid hockey fan was in the process of examining the factors that determine the success or failure of hockey teams.He noticed that teams with many rookies and teams with many veterans seem to do quite poorly.To further analyze his beliefs he took a random sample of 20 teams and proposed a second-order model with one independent variable,average years of professional experience.The selected model is y = β0 + β1x + β2x2 + ε,where y = winning team's percentage,and x = average years of professional experience.The computer output is shown below. THE REGRESSION EQUATION IS y = 32.6 + 5.96x− .48x2 S = 16.1 R−Sq = 43.9% ANALYSIS OF VARIANCE
S = 16.1 R−Sq = 43.9% ANALYSIS OF VARIANCE 
{Hockey Teams Narrative} Test to determine at the 10% significance level if the x2 term should be retained.
An avid hockey fan was in the process of examining the factors that determine the success or failure of hockey teams.He noticed that teams with many rookies and teams with many veterans seem to do quite poorly.To further analyze his beliefs he took a random sample of 20 teams and proposed a second-order model with one independent variable,average years of professional experience.The selected model is y = β0 + β1x + β2x2 + ε,where y = winning team's percentage,and x = average years of professional experience.The computer output is shown below. THE REGRESSION EQUATION IS y = 32.6 + 5.96x− .48x2
 S = 16.1 R−Sq = 43.9% ANALYSIS OF VARIANCE
S = 16.1 R−Sq = 43.9% ANALYSIS OF VARIANCE 
{Hockey Teams Narrative} Test to determine at the 10% significance level if the x2 term should be retained.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
61
Silver Prices
An economist is in the process of developing a model to predict the price of silver.She believes that the two most important variables are the price of a barrel of oil (x1)and the interest rate (x2).She proposes the first-order model with interaction: y = β0 + β1x1 + β2x2 + β3x1x3 + ε.A random sample of 20 daily observations was taken.The computer output is shown below. THE REGRESSION EQUATION IS y = 115.6 + 22.3x1 + 14.7x2− 1.36x1x2 S = 20.9 R−Sq = 55.4% ANALYSIS OF VARIANCE
S = 20.9 R−Sq = 55.4% ANALYSIS OF VARIANCE 
{Silver Prices Narrative} Interpret the coefficient b2.
An economist is in the process of developing a model to predict the price of silver.She believes that the two most important variables are the price of a barrel of oil (x1)and the interest rate (x2).She proposes the first-order model with interaction: y = β0 + β1x1 + β2x2 + β3x1x3 + ε.A random sample of 20 daily observations was taken.The computer output is shown below. THE REGRESSION EQUATION IS y = 115.6 + 22.3x1 + 14.7x2− 1.36x1x2
 S = 20.9 R−Sq = 55.4% ANALYSIS OF VARIANCE
S = 20.9 R−Sq = 55.4% ANALYSIS OF VARIANCE 
{Silver Prices Narrative} Interpret the coefficient b2.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
62
Motorcycle Fatalities
A traffic consultant has analyzed the factors that affect the number of motorcycle fatalities.She has come to the conclusion that two important variables are the number of motorcycle and the number of cars.She proposed the model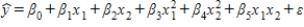 (the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS
(the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS 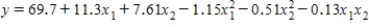
 S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE
S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE 
{Motorcycle Fatalities Narrative} Test at the 1% significance level to determine if the x1 term should be retained in the model.
A traffic consultant has analyzed the factors that affect the number of motorcycle fatalities.She has come to the conclusion that two important variables are the number of motorcycle and the number of cars.She proposed the model
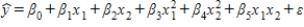 (the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS
(the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS 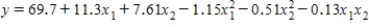
 S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE
S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE 
{Motorcycle Fatalities Narrative} Test at the 1% significance level to determine if the x1 term should be retained in the model.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
63
A first-order model was used in regression analysis involving 25 observations to study the relationship between a dependent variable y and three independent variables x1,x2,and x3.The analysis showed that the mean squares for regression is 160 and the sum of squares for error is 1050.In addition,the following is a partial computer printout. 
a.Develop the ANOVA table.
b.Is there enough evidence at the 5% significance level to conclude that the model is useful in predicting the value of y?
c.Test at the 5% significance level to determine whether x1 is linearly related to y.
d.Is there sufficient evidence at the 5% significance level to indicate that x2 is negatively linearly related to y?
e.Is there sufficient evidence at the 5% significance level to indicate that x3 is positively linearly related to y?

a.Develop the ANOVA table.
b.Is there enough evidence at the 5% significance level to conclude that the model is useful in predicting the value of y?
c.Test at the 5% significance level to determine whether x1 is linearly related to y.
d.Is there sufficient evidence at the 5% significance level to indicate that x2 is negatively linearly related to y?
e.Is there sufficient evidence at the 5% significance level to indicate that x3 is positively linearly related to y?

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
64
Motorcycle Fatalities
A traffic consultant has analyzed the factors that affect the number of motorcycle fatalities.She has come to the conclusion that two important variables are the number of motorcycle and the number of cars.She proposed the model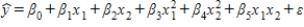 (the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS
(the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS 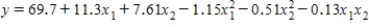
 S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE
S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE 
{Motorcycle Fatalities Narrative} Test at the 1% significance level to determine if the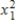 term should be retained in the model.
term should be retained in the model.
A traffic consultant has analyzed the factors that affect the number of motorcycle fatalities.She has come to the conclusion that two important variables are the number of motorcycle and the number of cars.She proposed the model
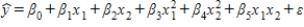 (the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS
(the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS 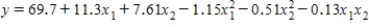
 S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE
S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE 
{Motorcycle Fatalities Narrative} Test at the 1% significance level to determine if the
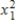 term should be retained in the model.
term should be retained in the model.
Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
65
Silver Prices
An economist is in the process of developing a model to predict the price of silver.She believes that the two most important variables are the price of a barrel of oil (x1)and the interest rate (x2).She proposes the first-order model with interaction: y = β0 + β1x1 + β2x2 + β3x1x3 + ε.A random sample of 20 daily observations was taken.The computer output is shown below. THE REGRESSION EQUATION IS y = 115.6 + 22.3x1 + 14.7x2− 1.36x1x2 S = 20.9 R−Sq = 55.4% ANALYSIS OF VARIANCE
S = 20.9 R−Sq = 55.4% ANALYSIS OF VARIANCE 
{Silver Prices Narrative} Do these results allow us at the 5% significance level to conclude that the model is useful in predicting the price of silver?
An economist is in the process of developing a model to predict the price of silver.She believes that the two most important variables are the price of a barrel of oil (x1)and the interest rate (x2).She proposes the first-order model with interaction: y = β0 + β1x1 + β2x2 + β3x1x3 + ε.A random sample of 20 daily observations was taken.The computer output is shown below. THE REGRESSION EQUATION IS y = 115.6 + 22.3x1 + 14.7x2− 1.36x1x2
 S = 20.9 R−Sq = 55.4% ANALYSIS OF VARIANCE
S = 20.9 R−Sq = 55.4% ANALYSIS OF VARIANCE 
{Silver Prices Narrative} Do these results allow us at the 5% significance level to conclude that the model is useful in predicting the price of silver?

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
66
Motorcycle Fatalities
A traffic consultant has analyzed the factors that affect the number of motorcycle fatalities.She has come to the conclusion that two important variables are the number of motorcycle and the number of cars.She proposed the model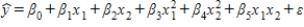 (the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS
(the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS 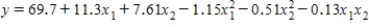
 S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE
S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE 
{Motorcycle Fatalities Narrative} What is the multiple coefficient of determination? What does this statistic tell you about the model?
A traffic consultant has analyzed the factors that affect the number of motorcycle fatalities.She has come to the conclusion that two important variables are the number of motorcycle and the number of cars.She proposed the model
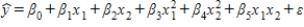 (the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS
(the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS 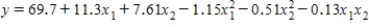
 S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE
S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE 
{Motorcycle Fatalities Narrative} What is the multiple coefficient of determination? What does this statistic tell you about the model?

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
67
Motorcycle Fatalities
A traffic consultant has analyzed the factors that affect the number of motorcycle fatalities.She has come to the conclusion that two important variables are the number of motorcycle and the number of cars.She proposed the model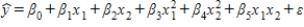 (the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS
(the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS 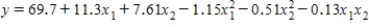
 S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE
S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE 
{Motorcycle Fatalities Narrative} What does the coefficient of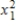 tell you about the model?
tell you about the model?
A traffic consultant has analyzed the factors that affect the number of motorcycle fatalities.She has come to the conclusion that two important variables are the number of motorcycle and the number of cars.She proposed the model
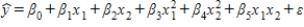 (the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS
(the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS 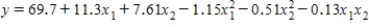
 S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE
S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE 
{Motorcycle Fatalities Narrative} What does the coefficient of
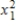 tell you about the model?
tell you about the model?
Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
68
Silver Prices
An economist is in the process of developing a model to predict the price of silver.She believes that the two most important variables are the price of a barrel of oil (x1)and the interest rate (x2).She proposes the first-order model with interaction: y = β0 + β1x1 + β2x2 + β3x1x3 + ε.A random sample of 20 daily observations was taken.The computer output is shown below. THE REGRESSION EQUATION IS y = 115.6 + 22.3x1 + 14.7x2− 1.36x1x2 S = 20.9 R−Sq = 55.4% ANALYSIS OF VARIANCE
S = 20.9 R−Sq = 55.4% ANALYSIS OF VARIANCE 
{Silver Prices Narrative} Is there sufficient evidence at the 1% significance level to conclude that the price of a barrel of oil and the price of silver are linearly related?
An economist is in the process of developing a model to predict the price of silver.She believes that the two most important variables are the price of a barrel of oil (x1)and the interest rate (x2).She proposes the first-order model with interaction: y = β0 + β1x1 + β2x2 + β3x1x3 + ε.A random sample of 20 daily observations was taken.The computer output is shown below. THE REGRESSION EQUATION IS y = 115.6 + 22.3x1 + 14.7x2− 1.36x1x2
 S = 20.9 R−Sq = 55.4% ANALYSIS OF VARIANCE
S = 20.9 R−Sq = 55.4% ANALYSIS OF VARIANCE 
{Silver Prices Narrative} Is there sufficient evidence at the 1% significance level to conclude that the price of a barrel of oil and the price of silver are linearly related?

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
69
Silver Prices
An economist is in the process of developing a model to predict the price of silver.She believes that the two most important variables are the price of a barrel of oil (x1)and the interest rate (x2).She proposes the first-order model with interaction: y = β0 + β1x1 + β2x2 + β3x1x3 + ε.A random sample of 20 daily observations was taken.The computer output is shown below. THE REGRESSION EQUATION IS y = 115.6 + 22.3x1 + 14.7x2− 1.36x1x2 S = 20.9 R−Sq = 55.4% ANALYSIS OF VARIANCE
S = 20.9 R−Sq = 55.4% ANALYSIS OF VARIANCE 
{Silver Prices Narrative} Is there sufficient evidence at the 1% significance level to conclude that the interaction term should be retained?
An economist is in the process of developing a model to predict the price of silver.She believes that the two most important variables are the price of a barrel of oil (x1)and the interest rate (x2).She proposes the first-order model with interaction: y = β0 + β1x1 + β2x2 + β3x1x3 + ε.A random sample of 20 daily observations was taken.The computer output is shown below. THE REGRESSION EQUATION IS y = 115.6 + 22.3x1 + 14.7x2− 1.36x1x2
 S = 20.9 R−Sq = 55.4% ANALYSIS OF VARIANCE
S = 20.9 R−Sq = 55.4% ANALYSIS OF VARIANCE 
{Silver Prices Narrative} Is there sufficient evidence at the 1% significance level to conclude that the interaction term should be retained?

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
70
Silver Prices
An economist is in the process of developing a model to predict the price of silver.She believes that the two most important variables are the price of a barrel of oil (x1)and the interest rate (x2).She proposes the first-order model with interaction: y = β0 + β1x1 + β2x2 + β3x1x3 + ε.A random sample of 20 daily observations was taken.The computer output is shown below. THE REGRESSION EQUATION IS y = 115.6 + 22.3x1 + 14.7x2− 1.36x1x2 S = 20.9 R−Sq = 55.4% ANALYSIS OF VARIANCE
S = 20.9 R−Sq = 55.4% ANALYSIS OF VARIANCE 
{Silver Prices Narrative} Interpret the coefficient b1.
An economist is in the process of developing a model to predict the price of silver.She believes that the two most important variables are the price of a barrel of oil (x1)and the interest rate (x2).She proposes the first-order model with interaction: y = β0 + β1x1 + β2x2 + β3x1x3 + ε.A random sample of 20 daily observations was taken.The computer output is shown below. THE REGRESSION EQUATION IS y = 115.6 + 22.3x1 + 14.7x2− 1.36x1x2
 S = 20.9 R−Sq = 55.4% ANALYSIS OF VARIANCE
S = 20.9 R−Sq = 55.4% ANALYSIS OF VARIANCE 
{Silver Prices Narrative} Interpret the coefficient b1.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
71
It is not possible to incorporate nominal variables into a regression model.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
72
Motorcycle Fatalities
A traffic consultant has analyzed the factors that affect the number of motorcycle fatalities.She has come to the conclusion that two important variables are the number of motorcycle and the number of cars.She proposed the model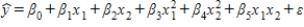 (the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS
(the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS 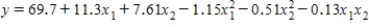
 S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE
S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE 
{Motorcycle Fatalities Narrative} Test at the 1% significance level to determine if the interaction term should be retained in the model.
A traffic consultant has analyzed the factors that affect the number of motorcycle fatalities.She has come to the conclusion that two important variables are the number of motorcycle and the number of cars.She proposed the model
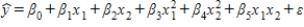 (the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS
(the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS 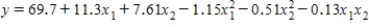
 S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE
S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE 
{Motorcycle Fatalities Narrative} Test at the 1% significance level to determine if the interaction term should be retained in the model.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
73
In explaining the amount of money spent on gifts for a child's birthday each year,the independent variable,age of child,is best represented by a dummy variable.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
74
Motorcycle Fatalities
A traffic consultant has analyzed the factors that affect the number of motorcycle fatalities.She has come to the conclusion that two important variables are the number of motorcycle and the number of cars.She proposed the model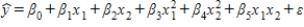 (the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS
(the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS 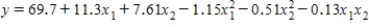
 S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE
S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE 
{Motorcycle Fatalities Narrative} Test at the 1% significance level to determine if the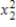 term should be retained in the model.
term should be retained in the model.
A traffic consultant has analyzed the factors that affect the number of motorcycle fatalities.She has come to the conclusion that two important variables are the number of motorcycle and the number of cars.She proposed the model
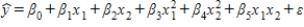 (the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS
(the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS 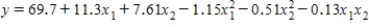
 S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE
S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE 
{Motorcycle Fatalities Narrative} Test at the 1% significance level to determine if the
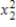 term should be retained in the model.
term should be retained in the model.
Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
75
Silver Prices
An economist is in the process of developing a model to predict the price of silver.She believes that the two most important variables are the price of a barrel of oil (x1)and the interest rate (x2).She proposes the first-order model with interaction: y = β0 + β1x1 + β2x2 + β3x1x3 + ε.A random sample of 20 daily observations was taken.The computer output is shown below. THE REGRESSION EQUATION IS y = 115.6 + 22.3x1 + 14.7x2− 1.36x1x2 S = 20.9 R−Sq = 55.4% ANALYSIS OF VARIANCE
S = 20.9 R−Sq = 55.4% ANALYSIS OF VARIANCE 
{Silver Prices Narrative} Is there sufficient evidence at the 1% significance level to conclude that the interest rate and the price of silver are linearly related?
An economist is in the process of developing a model to predict the price of silver.She believes that the two most important variables are the price of a barrel of oil (x1)and the interest rate (x2).She proposes the first-order model with interaction: y = β0 + β1x1 + β2x2 + β3x1x3 + ε.A random sample of 20 daily observations was taken.The computer output is shown below. THE REGRESSION EQUATION IS y = 115.6 + 22.3x1 + 14.7x2− 1.36x1x2
 S = 20.9 R−Sq = 55.4% ANALYSIS OF VARIANCE
S = 20.9 R−Sq = 55.4% ANALYSIS OF VARIANCE 
{Silver Prices Narrative} Is there sufficient evidence at the 1% significance level to conclude that the interest rate and the price of silver are linearly related?

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
76
In regression analysis,a nominal independent variable such as color,with three different categories such as red,white,and blue,is best represented by three indicator variables to represent the three colors.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
77
In regression analysis,indicator variables are also called dependent variables.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
78
An indicator variable (also called a dummy variable)is a variable that can assume either one of two values (usually 0 and 1),where one value represents the existence of a certain condition,and the other value indicates that the condition does not hold.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
79
Motorcycle Fatalities
A traffic consultant has analyzed the factors that affect the number of motorcycle fatalities.She has come to the conclusion that two important variables are the number of motorcycle and the number of cars.She proposed the model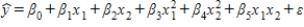 (the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS
(the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS 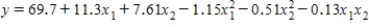
 S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE
S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE 
{Motorcycle Fatalities Narrative} Test at the 1% significance level to determine if the x2 term should be retained in the model.
A traffic consultant has analyzed the factors that affect the number of motorcycle fatalities.She has come to the conclusion that two important variables are the number of motorcycle and the number of cars.She proposed the model
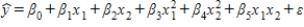 (the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS
(the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS 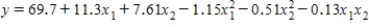
 S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE
S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE 
{Motorcycle Fatalities Narrative} Test at the 1% significance level to determine if the x2 term should be retained in the model.

Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck
80
Motorcycle Fatalities
A traffic consultant has analyzed the factors that affect the number of motorcycle fatalities.She has come to the conclusion that two important variables are the number of motorcycle and the number of cars.She proposed the model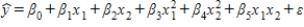 (the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS
(the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS 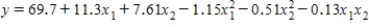
 S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE
S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE 
{Motorcycle Fatalities Narrative} What does the coefficient of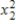 tell you about the model?
tell you about the model?
A traffic consultant has analyzed the factors that affect the number of motorcycle fatalities.She has come to the conclusion that two important variables are the number of motorcycle and the number of cars.She proposed the model
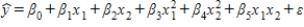 (the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS
(the second-order model with interaction),where y = number of annual fatalities per county,x1 = number of motorcycles registered in the county (in 10,000),and x2 = number of cars registered in the county (in 1000).The computer output (based on a random sample of 35 counties)is shown below: THE REGRESSION EQUATION IS 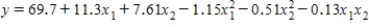
 S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE
S = 15.2 R−Sq = 47.2% ANALYSIS OF VARIANCE 
{Motorcycle Fatalities Narrative} What does the coefficient of
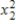 tell you about the model?
tell you about the model?
Unlock Deck
Unlock for access to all 148 flashcards in this deck.
Unlock Deck
k this deck


