Deck 9: Linear Programming
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/34
Play
Full screen (f)
Deck 9: Linear Programming
1
For costs to be a linear function of output:
A) returns to each factor input must be constant.
B) input prices must change at a constant rate.
C) product prices must be constant.
D) returns to scale must be constant.
A) returns to each factor input must be constant.
B) input prices must change at a constant rate.
C) product prices must be constant.
D) returns to scale must be constant.
D
2
Net profits equals profit contribution minus:
A) variable costs.
B) total costs.
C) average total costs.
D) fixed costs.
A) variable costs.
B) total costs.
C) average total costs.
D) fixed costs.
D
3
When an LP objective function is to maximize profits:
A) resource constraints must be of the £ variety.
B) resource constraints must be of the ³ variety.
C) all input costs must be variable.
D) the total revenue function must not be linear.
A) resource constraints must be of the £ variety.
B) resource constraints must be of the ³ variety.
C) all input costs must be variable.
D) the total revenue function must not be linear.
A
4
Constrained profit maximization requires:
A) no excess capacity.
B) excess capacity.
C) a linear profit function.
D) constrained maximization of the total profit contribution.
A) no excess capacity.
B) excess capacity.
C) a linear profit function.
D) constrained maximization of the total profit contribution.

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
5
Profit contribution equals total:
A) revenue minus variable cost.
B) revenue minus fixed cost.
C) profit.
D) revenue minus total cost.
A) revenue minus variable cost.
B) revenue minus fixed cost.
C) profit.
D) revenue minus total cost.

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
6
If the objective function is to maximize revenue subject to a binding labor constraint, then the shadow price of labor is:
A) the marginal product of labor.
B) the marginal revenue product of labor.
C) negative.
D) zero.
A) the marginal product of labor.
B) the marginal revenue product of labor.
C) negative.
D) zero.

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
7
Combinations of products that generate the same level of profit are shown graphically by:
A) an isocost curve.
B) an isoprofit curve.
C) an isoquant curve.
D) a feasible space.
A) an isocost curve.
B) an isoprofit curve.
C) an isoquant curve.
D) a feasible space.

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
8
If X > 0 in the primal solution:
A) the marginal value of inputs just equals the marginal value of output in X production.
B) the marginal value of inputs exceeds the marginal value of output in X production.
C) LX > 0 in the dual solution.
D) LX < 0 in the dual solution.
A) the marginal value of inputs just equals the marginal value of output in X production.
B) the marginal value of inputs exceeds the marginal value of output in X production.
C) LX > 0 in the dual solution.
D) LX < 0 in the dual solution.

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
9
Linear programming assumes:
A) falling input prices.
B) increasing returns to each factor input.
C) straight-line objective and constraint functions.
D) monopolistic competition.
A) falling input prices.
B) increasing returns to each factor input.
C) straight-line objective and constraint functions.
D) monopolistic competition.

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
10
If QA > 0, then the marginal value of inputs employed:
A) equals the marginal value of output.
B) is less than the marginal value of output.
C) equals current input prices.
D) exceeds the marginal value of output.
A) equals the marginal value of output.
B) is less than the marginal value of output.
C) equals current input prices.
D) exceeds the marginal value of output.

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
11
Linear programming is an analytical technique used to:
A) solve constrained optimization problems.
B) project trends.
C) increase worker productivity.
D) estimate linear demand functions.
A) solve constrained optimization problems.
B) project trends.
C) increase worker productivity.
D) estimate linear demand functions.

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
12
When the costs of all inputs rise by a given percentage, the isocost line:
A) slope decreases.
B) slope is unaffected.
C) and objective function intersection will be unaffected.
D) slope increases.
A) slope decreases.
B) slope is unaffected.
C) and objective function intersection will be unaffected.
D) slope increases.

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
13
When the primal LP problem is to maximize revenue subject to various input constraints, the shadow prices of inputs in the dual constraints:
A) equal the marginal revenue product of each input.
B) are positive for inputs with excess capacity.
C) equals zero for fully utilized inputs.
D) equal the marginal product of each input.
A) equal the marginal revenue product of each input.
B) are positive for inputs with excess capacity.
C) equals zero for fully utilized inputs.
D) equal the marginal product of each input.

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
14
If the primal objective function is to minimize cost subject to output constraints, the dual objective function is to maximize:
A) revenue.
B) profits.
C) output.
D) the value of inputs employed.
A) revenue.
B) profits.
C) output.
D) the value of inputs employed.

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
15
To determine the quantity to be produced by each production process at varying points along an isoquant, managers could use:
A) the point-slope method.
B) slack variable method.
C) the relative distance method.
D) the relative cost method.
A) the point-slope method.
B) slack variable method.
C) the relative distance method.
D) the relative cost method.

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
16
Slack variables:
A) allow constraint equations to be expressed as inequalities.
B) measure excess capacity.
C) never equal zero.
D) in some cases have negative values.
A) allow constraint equations to be expressed as inequalities.
B) measure excess capacity.
C) never equal zero.
D) in some cases have negative values.

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
17
Unit costs are always constant if:
A) input prices are constant.
B) the total cost function is linear.
C) constant returns to scale are operative.
D) input prices are constant and the total cost function is linear.
A) input prices are constant.
B) the total cost function is linear.
C) constant returns to scale are operative.
D) input prices are constant and the total cost function is linear.

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
18
If the capital slack variable = 0, then:
A) the shadow price on capital is > 0.
B) the marginal product of capital = 0.
C) the marginal revenue product of capital = 0.
D) excess capital capacity exists.
A) the shadow price on capital is > 0.
B) the marginal product of capital = 0.
C) the marginal revenue product of capital = 0.
D) excess capital capacity exists.

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
19
When the objective function coincides with the boundary of the feasible space:
A) an optimal solution cannot be determined.
B) there is only one optimal solution.
C) there are many possible optimal solutions.
D) an optimal solution does not exist.
A) an optimal solution cannot be determined.
B) there is only one optimal solution.
C) there are many possible optimal solutions.
D) an optimal solution does not exist.

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
20
For managerial decision problems analyzed using the LP approach:
A) some input costs must be fixed.
B) all input costs must be fixed.
C) increasing returns to scale must predominate.
D) returns to each factor input must be constant.
A) some input costs must be fixed.
B) all input costs must be fixed.
C) increasing returns to scale must predominate.
D) returns to each factor input must be constant.

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
21
Profit Maximization. Samantha Spade & Associates, Ltd. is a small architectural firm located in Portland, Oregon, specializing in the preparation of multi-family residential housing complex, R, and commercial retails, C, architectural designs. Prevailing prices in the market are $10,000 for residential housing designs and $25,000 for commercial retail designs.
Six architects run the firm, and work a 50-hour workweek, 50 weeks per year. They are assisted by six drafting personnel and two secretaries, all of whom work a typical 40-hour workweek, 50 weeks per year. The firm must decide how to target its promotional efforts so as to best use its resources during the coming year. Based on previous experience, the firm expects that an average of 150 hours of architect and 100 hours of drafting time will be required for each residential housing complex design, whereas commercial retail design will require an average of 250 architect hours and 200 drafting hours. Fifty hours of secretarial time will also be required for each architectural design. In addition, variable computer and other processing costs are expected to average $1,000 per residential design and $1,500 per commercial retail design.
A. Set up the linear programming problem the firm would use to determine the profit-maximizing output levels for residential and commercial designs. Show both the inequality and equality forms of the constraint conditions.
B. Completely solve and interpret the solution values for the linear programming problem.
C. Calculate maximum possible net profits per year for the firm assuming that architects draw a salary of $100,000 per year, drafting personnel earn $65,000 per year, secretaries are paid $20 per hour, and fixed overhead (including promotion and other expenses) averages $50,000.
D. After considering the above data, one senior architect recommended reducing one drafting personnel to part-time status (adjusting salary accordingly) while retaining the rest of the current staff full-time. What are net profits per year under this suggestion?
Six architects run the firm, and work a 50-hour workweek, 50 weeks per year. They are assisted by six drafting personnel and two secretaries, all of whom work a typical 40-hour workweek, 50 weeks per year. The firm must decide how to target its promotional efforts so as to best use its resources during the coming year. Based on previous experience, the firm expects that an average of 150 hours of architect and 100 hours of drafting time will be required for each residential housing complex design, whereas commercial retail design will require an average of 250 architect hours and 200 drafting hours. Fifty hours of secretarial time will also be required for each architectural design. In addition, variable computer and other processing costs are expected to average $1,000 per residential design and $1,500 per commercial retail design.
A. Set up the linear programming problem the firm would use to determine the profit-maximizing output levels for residential and commercial designs. Show both the inequality and equality forms of the constraint conditions.
B. Completely solve and interpret the solution values for the linear programming problem.
C. Calculate maximum possible net profits per year for the firm assuming that architects draw a salary of $100,000 per year, drafting personnel earn $65,000 per year, secretaries are paid $20 per hour, and fixed overhead (including promotion and other expenses) averages $50,000.
D. After considering the above data, one senior architect recommended reducing one drafting personnel to part-time status (adjusting salary accordingly) while retaining the rest of the current staff full-time. What are net profits per year under this suggestion?

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
22
If slack exists in the solution of the primal LP, the dual shadow price variable is:
A) zero.
B) positive.
C) negative.
D) none of these.
A) zero.
B) positive.
C) negative.
D) none of these.

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
23
The cost of capacity subject to constraints is:
A) variable.
B) sunk.
C) semi-variable.
D) nonzero.
A) variable.
B) sunk.
C) semi-variable.
D) nonzero.

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
24
Optimal Production. Canine Products, Inc., produces and markets a new moist and chewy nugget dog food called "Chow Hound" being test marketed in the San Diego market. This product is similar to several others offered by Canine Products, and can be produced with currently available equipment and personnel using any of three alternative product methods. Method A requires 6 hours of labor and 1 processing facility hour to produce 100 bags of dog food, QA. Method B requires 3 labor and 3 processing facility hours per QB. Method C requires 2 labor hours and 4 processing facility hours per unit of QC. Because of slack demand for other products CP currently has 15 labor hours and 5 processing facility hours available per week for producing Chow Hound.
A. Using the equality form of the constraint conditions, set up and interpret the linear program Canine Products would use to maximize production of Chow Hound given currently available resources.
B. Calculate and interpret all solution values.
A. Using the equality form of the constraint conditions, set up and interpret the linear program Canine Products would use to maximize production of Chow Hound given currently available resources.
B. Calculate and interpret all solution values.

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
25
If a linear programming problem involves the minimization of advertising costs subject to audience marital status and income constraints, the objective function is:
A) the marital status constraint.
B) the individual income constraint.
C) the advertising cost function.
D) none of these.
A) the marital status constraint.
B) the individual income constraint.
C) the advertising cost function.
D) none of these.

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
26
A negative value for a given slack variable implies:
A) no excess capacity.
B) use of more resources than are available.
C) none of the above.
D) excess capacity.
A) no excess capacity.
B) use of more resources than are available.
C) none of the above.
D) excess capacity.

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
27
Fixed Input Relations. Extreme Biking, Inc., assembles high-end extreme mountain bicycles at a plant in Lexington, Massachusetts. The plant uses labor (L) and capital (K) in an assembly line process to produce output (Q) where:
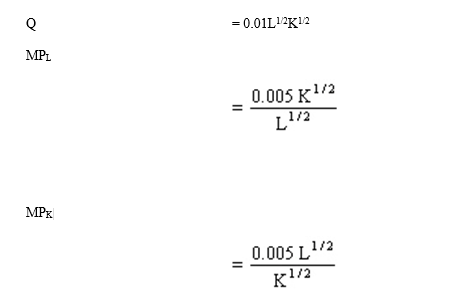
A. Calculate how many units of output can be produced with 25 units of labor and 400 units of capital, and with 225 units of labor and 3,600 units of capital. Are returns to scale increasing, constant, or diminishing?
B. Calculate the change in the marginal product of labor as labor grows from 25 to 36 units, holding capital constant at 400 units. Similarly, calculate the change in the marginal product of capital as capital grows from 400 to 625 units, holding labor constant at 25 units. Are returns to each factor increasing, constant, or diminishing?
C. Assume now and throughout the remainder of the problem that labor and capital must be combined in the ratio 25L:400K. How much output could be produced if the company faces a constraint of L = 25,000 and K = 500,000 during the coming production period?
D. What are the marginal products of each factor under the conditions described in part C?
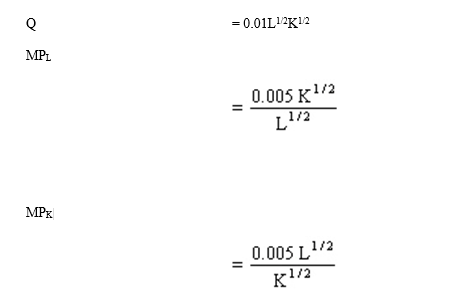
A. Calculate how many units of output can be produced with 25 units of labor and 400 units of capital, and with 225 units of labor and 3,600 units of capital. Are returns to scale increasing, constant, or diminishing?
B. Calculate the change in the marginal product of labor as labor grows from 25 to 36 units, holding capital constant at 400 units. Similarly, calculate the change in the marginal product of capital as capital grows from 400 to 625 units, holding labor constant at 25 units. Are returns to each factor increasing, constant, or diminishing?
C. Assume now and throughout the remainder of the problem that labor and capital must be combined in the ratio 25L:400K. How much output could be produced if the company faces a constraint of L = 25,000 and K = 500,000 during the coming production period?
D. What are the marginal products of each factor under the conditions described in part C?

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
28
Linear Programming Concepts. Indicate whether each of the following statements is true or false. Defend your answer.
A. Linear programming can be used for solving any type of constrained optimization problem where the relations involved can be approximated by linear equations.
B. Linear revenue, cost and profit relations will be observed when output prices, input prices, and average variable costs are constant.
C. Equal distances along a given production process ray in a linear programming problem always represent an identical level of output
D. At isoquant segment midpoints, each adjacent production process must be used to produce 50% of output efficiently.
E. Maximizing a LP profit contribution objective function always results in also maximizing total net profits.
A. Linear programming can be used for solving any type of constrained optimization problem where the relations involved can be approximated by linear equations.
B. Linear revenue, cost and profit relations will be observed when output prices, input prices, and average variable costs are constant.
C. Equal distances along a given production process ray in a linear programming problem always represent an identical level of output
D. At isoquant segment midpoints, each adjacent production process must be used to produce 50% of output efficiently.
E. Maximizing a LP profit contribution objective function always results in also maximizing total net profits.

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
29
Optimal Lending. Penny Lane is a senior loan officer with Citrus National Bank in Tampa, Florida. Lane has both corporate and personal lending customers. On average, the profit contribution margin or interest rate spread is 1.75% on corporate loans and 2.25% on personal loans. This return difference reflects the fact that personal loans tend to be riskier than corporate loans. Lane seeks to maximize the total dollar profit contribution earned, subject to a variety of restrictions on her lending practices. In order to limit default risk, Lane must restrict personal loans to no more than 40% of total loans outstanding. Similarly, to ensure adequate diversification against business cycle risk, corporate lending cannot exceed 80% of loaned funds. To maintain good customer relations by serving the basic needs of the local business community, Lane has decided to extend at least 40% of her total credit authorization to corporate customers on an ongoing basis. Finally, Lane cannot exceed her current total credit authorization of $50 million.
A. Using the inequality form of the constraint conditions, set up and interpret the linear programming problem Lane would use to determine the optimal dollar amount of credit to extend to corporate (C) and personal (P) lending customers. Also formulate the LP problem using the equality form of the constraint conditions.
B. Use a graph to determine the optimal solution, and check your solution algebraically. Fully interpret solution values.
A. Using the inequality form of the constraint conditions, set up and interpret the linear programming problem Lane would use to determine the optimal dollar amount of credit to extend to corporate (C) and personal (P) lending customers. Also formulate the LP problem using the equality form of the constraint conditions.
B. Use a graph to determine the optimal solution, and check your solution algebraically. Fully interpret solution values.

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
30
Optimal Production. Ozark Telephone, Inc. (OTI) is a small telephone company offering local dial-tone service to its franchised areas in rural southeastern Missouri. A new office park development site is being planned within OTI's territory and John Sample, a network engineer, has to maximize the conversation capacity per line under cost and technology constraints using both traditional copper-wire lines and new fiber-optic lines.
OTI wants to gradually move into the all-digital communication environment possible with fiber-optics, so a company policy has been adopted specifying that at least 3 fiber-optic lines be employed for every 2 copper lines on new installations. To minimize the need to quickly retrain its linemen, OTI wants at least 30% of new telephone lines installed to be copper. No existing telephone facilities run to the development site, and OTI must use its own facilities to carry the traffic (it cannot lease capacity from any other local telephone company). Finally, current costs and technologies dictate that 1 fiber line can carry the equivalent of 5 copper lines at the same cost to OTI. That is, if one copper line can carry one telephone conversation, fiber optic lines can carry five conversations at no cost penalty. Sample's objective is to maximize the capacity per line of the transmissions facilities being built to carry traffic to/from the office park.
A. Using the inequality form of the constraint conditions, set up and interpret the linear programming problem Sample would use to determine the optimal percentage of copper and fiber-optic lines. Also formulate the problem using the equality form of the constraint conditions.
B. With a graph, determine the optimal solution; check your solution algebraically. Fully interpret solution values.
C. Holding all else equal, how much would the capacity of fiber optic lines have to fall to alter the optimal construction mix determined in part B?
D. Calculate the opportunity cost, measured in terms of conversation capacity per line, of OTI's 30% copper line constraint.
OTI wants to gradually move into the all-digital communication environment possible with fiber-optics, so a company policy has been adopted specifying that at least 3 fiber-optic lines be employed for every 2 copper lines on new installations. To minimize the need to quickly retrain its linemen, OTI wants at least 30% of new telephone lines installed to be copper. No existing telephone facilities run to the development site, and OTI must use its own facilities to carry the traffic (it cannot lease capacity from any other local telephone company). Finally, current costs and technologies dictate that 1 fiber line can carry the equivalent of 5 copper lines at the same cost to OTI. That is, if one copper line can carry one telephone conversation, fiber optic lines can carry five conversations at no cost penalty. Sample's objective is to maximize the capacity per line of the transmissions facilities being built to carry traffic to/from the office park.
A. Using the inequality form of the constraint conditions, set up and interpret the linear programming problem Sample would use to determine the optimal percentage of copper and fiber-optic lines. Also formulate the problem using the equality form of the constraint conditions.
B. With a graph, determine the optimal solution; check your solution algebraically. Fully interpret solution values.
C. Holding all else equal, how much would the capacity of fiber optic lines have to fall to alter the optimal construction mix determined in part B?
D. Calculate the opportunity cost, measured in terms of conversation capacity per line, of OTI's 30% copper line constraint.

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
31
LP Basics. Indicate whether each of the following statements is true or false and why.
A. In profit maximization linear programming problems, negative values for slack variables are impossible.
B. Binding constraints indicate positive slack variables at the optimum solution.
C. Points not on process rays represent unattainable technologies.
D. Constant input prices is the only requirement for a total cost function to be linear.
E. Changing input prices will not alter the slope of a given isoquant line.
A. In profit maximization linear programming problems, negative values for slack variables are impossible.
B. Binding constraints indicate positive slack variables at the optimum solution.
C. Points not on process rays represent unattainable technologies.
D. Constant input prices is the only requirement for a total cost function to be linear.
E. Changing input prices will not alter the slope of a given isoquant line.

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck
32
When some capacity constraints are binding, although others are nonbinding:
A) the shadow price for new capacity is positive.
B) the shadow price for output is positive.
C) the marginal revenue product for new capacity is positive.
D) the marginal product of new capacity is positive.
A) the shadow price for new capacity is positive.
B) the shadow price for output is positive.
C) the marginal revenue product for new capacity is positive.
D) the marginal product of new capacity is positive.

Unlock Deck
Unlock for access to all 34 flashcards in this deck.
Unlock Deck
k this deck


