Exam 9: Linear Programming
Exam 1: Nature and Scope of Managerial Economics25 Questions
Exam 2: Economic Optimization45 Questions
Exam 3: Demand and Supply50 Questions
Exam 4: Demand Analysis46 Questions
Exam 5: Demand Estimation49 Questions
Exam 6: Forecasting50 Questions
Exam 7: Production Analysis and Compensation Policy50 Questions
Exam 8: Cost Analysis and Estimation50 Questions
Exam 9: Linear Programming32 Questions
Exam 10: Competitive Markets50 Questions
Exam 11: Performance and Strategy in Competitive Markets50 Questions
Exam 12: Monopoly and Monopsony50 Questions
Exam 13: Monopolistic Competition and Oligopoly48 Questions
Exam 14: Game Theory and Competitive Strategy37 Questions
Exam 15: Pricing Practices47 Questions
Exam 16: Risk Analysis47 Questions
Exam 17: Capital Budgeting50 Questions
Exam 18: Organization Structure and Corporate Governance50 Questions
Exam 19: Government in the Market Economy50 Questions
Select questions type
A negative value for a given slack variable implies:
Free
(Multiple Choice)
4.7/5  (41)
(41)
Correct Answer:
B
If a linear programming problem involves the minimization of advertising costs subject to audience marital status and income constraints, the objective function is:
Free
(Multiple Choice)
4.7/5  (42)
(42)
Correct Answer:
C
Combinations of products that generate the same level of profit are shown graphically by:
(Multiple Choice)
4.8/5  (38)
(38)
When the costs of all inputs rise by a given percentage, the isocost line:
(Multiple Choice)
4.8/5  (41)
(41)
When the objective function coincides with the boundary of the feasible space:
(Multiple Choice)
4.8/5  (32)
(32)
When the primal LP problem is to maximize revenue subject to various input constraints, the shadow prices of inputs in the dual constraints:
(Multiple Choice)
5.0/5  (35)
(35)
If the objective function is to maximize revenue subject to a binding labor constraint, then the shadow price of labor is:
(Multiple Choice)
4.8/5  (34)
(34)
Fixed Input Relations. Extreme Biking, Inc., assembles high-end extreme mountain bicycles at a plant in Lexington, Massachusetts. The plant uses labor (L) and capital (K) in an assembly line process to produce output (Q) where:
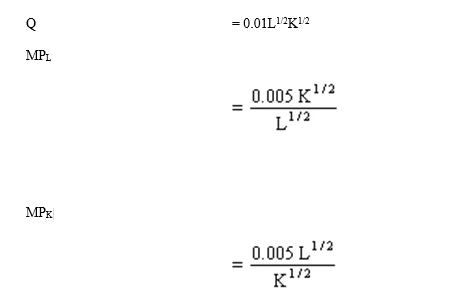 A. Calculate how many units of output can be produced with 25 units of labor and 400 units of capital, and with 225 units of labor and 3,600 units of capital. Are returns to scale increasing, constant, or diminishing?
B. Calculate the change in the marginal product of labor as labor grows from 25 to 36 units, holding capital constant at 400 units. Similarly, calculate the change in the marginal product of capital as capital grows from 400 to 625 units, holding labor constant at 25 units. Are returns to each factor increasing, constant, or diminishing?
C. Assume now and throughout the remainder of the problem that labor and capital must be combined in the ratio 25L:400K. How much output could be produced if the company faces a constraint of L = 25,000 and K = 500,000 during the coming production period?
D. What are the marginal products of each factor under the conditions described in part C?
A. Calculate how many units of output can be produced with 25 units of labor and 400 units of capital, and with 225 units of labor and 3,600 units of capital. Are returns to scale increasing, constant, or diminishing?
B. Calculate the change in the marginal product of labor as labor grows from 25 to 36 units, holding capital constant at 400 units. Similarly, calculate the change in the marginal product of capital as capital grows from 400 to 625 units, holding labor constant at 25 units. Are returns to each factor increasing, constant, or diminishing?
C. Assume now and throughout the remainder of the problem that labor and capital must be combined in the ratio 25L:400K. How much output could be produced if the company faces a constraint of L = 25,000 and K = 500,000 during the coming production period?
D. What are the marginal products of each factor under the conditions described in part C?
(Essay)
5.0/5  (45)
(45)
LP Basics. Indicate whether each of the following statements is true or false and why.
A. In profit maximization linear programming problems, negative values for slack variables are impossible.
B. Binding constraints indicate positive slack variables at the optimum solution.
C. Points not on process rays represent unattainable technologies.
D. Constant input prices is the only requirement for a total cost function to be linear.
E. Changing input prices will not alter the slope of a given isoquant line.
(Short Answer)
4.8/5  (39)
(39)
When some capacity constraints are binding, although others are nonbinding:
(Multiple Choice)
4.9/5  (34)
(34)
To determine the quantity to be produced by each production process at varying points along an isoquant, managers could use:
(Multiple Choice)
4.8/5  (41)
(41)
Showing 1 - 20 of 32
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)