Deck 43: Molecules and Solids
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/46
Play
Full screen (f)
Deck 43: Molecules and Solids
1
The frequency of a microwave absorbed by a molecule when changing from the J = 3 to J = 4 rotation energy state is 4.61 × 1011 Hz.The moment of inertia of the molecule (in kg ⋅ m2)is
A)5.70 × 10−45
B)1.45 × 10−46
C)1.12 × 10−44
D)2.91 × 10−46
E)9.11 × 10−46
A)5.70 × 10−45
B)1.45 × 10−46
C)1.12 × 10−44
D)2.91 × 10−46
E)9.11 × 10−46
1.45 × 10−46
2
The force constant of HCl is 480 N/m.If the atomic masses are 1 u and 35 u (1 u = 1.66 × 10−27 kg),find the fundamental frequency (in Hz).
A)6.4 × 1013
B)9.2 × 1013
C)7.7 × 1013
D)8.7 × 1013
E)1.4 × 1013
A)6.4 × 1013
B)9.2 × 1013
C)7.7 × 1013
D)8.7 × 1013
E)1.4 × 1013
8.7 × 1013
3
Which of the following refer to the basic categories associated with the energy of a single molecule in a gaseous phase?
A)nuclear,electronic,interval
B)electronic,translation,rotation,vibration
C)ionic,covalent,hydrogen,Van der Waals
D)translation,rotation,vibration
E)dipole-dipole,covalent,ionic,translation
A)nuclear,electronic,interval
B)electronic,translation,rotation,vibration
C)ionic,covalent,hydrogen,Van der Waals
D)translation,rotation,vibration
E)dipole-dipole,covalent,ionic,translation
electronic,translation,rotation,vibration
4
An experiment determines that there are 49 allowed rotational energies for a diatomic molecule whose moment of inertia is 2 × 10−46 kg ⋅ m2.The maximum rotational kinetic energy (in eV)is
A)0.6
B)0.2
C)0.4
D)0.8
E)1.0
A)0.6
B)0.2
C)0.4
D)0.8
E)1.0

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
5
Assume a diatomic molecule can be considered to be two point masses separated by a distance r.The center of mass of the system is located a distance x from m1,equal to
A)m1r/(m1 + m2)
B)m2r/(m1 + m2)
C)(m1 + m2)r/m1
D)(m1 + m2)r/m2
E)r(m2/m1)
A)m1r/(m1 + m2)
B)m2r/(m1 + m2)
C)(m1 + m2)r/m1
D)(m1 + m2)r/m2
E)r(m2/m1)

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
6
The rotation spectrum of the HCl molecule has been observed in the far infrared,around 50 × 10−6 m.The spacing between successive lines in the spectrum corresponds to radiation of wavelength equal to 5 microns (1 μm = 10−6 m).Determine the frequency of the photon associated with this transition.
A)6 × 1014 Hz
B)6 × 1012 Hz
C)6 × 1011 Hz
D)6 × 1013 Hz
E)6 × 1010 Hz
A)6 × 1014 Hz
B)6 × 1012 Hz
C)6 × 1011 Hz
D)6 × 1013 Hz
E)6 × 1010 Hz

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
7
A diatomic molecule consists of two point masses,m1 and m2,separated by a distance r.Find the moment of inertia through the center of mass about an axis perpendicular to the molecular axis.
A)m1m2r2/(m1 + m2)
B)[(m1m2/m1)+ m2]r2
C)(m1 + m2)/m1m2r2
D)(m1 + m1)r2 /m1m2
E)m1m2r2/m1
A)m1m2r2/(m1 + m2)
B)[(m1m2/m1)+ m2]r2
C)(m1 + m2)/m1m2r2
D)(m1 + m1)r2 /m1m2
E)m1m2r2/m1

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
8
How many degrees of freedom does a diatomic molecule have?
A)3
B)6
C)5
D)7
E)9
A)3
B)6
C)5
D)7
E)9

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
9
The rotation spectrum of the HCl molecule suggests a photon in the far infrared (around 5.0 × 10−6 m)can excite the first rotational level.From this data,the moment of inertia of the HCl molecule (in kg ⋅ m2)is
A)2.8 × 10−48
B)2.8 × 10−49
C)2.8 × 10−47
D)2.8 × 10−46
E)2.8 × 10−45
A)2.8 × 10−48
B)2.8 × 10−49
C)2.8 × 10−47
D)2.8 × 10−46
E)2.8 × 10−45

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
10
The rotational kinetic energy of a diatomic molecule can take the form
A)(1/2)mω2
B)(1/2)Iω2
C)[m1m2/(m1 + m2)]r2ω2
D)(1/2)mv2
E)1/2 μω2
A)(1/2)mω2
B)(1/2)Iω2
C)[m1m2/(m1 + m2)]r2ω2
D)(1/2)mv2
E)1/2 μω2

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
11
The moment of inertia of a CO molecule is 1.46 × 10−46 kg ⋅ m2.What is the wavelength of the photon emitted if a rotational transition occurs from the J = 3 to the J = 2 state?
A)4.36 × 10−4 m
B)8.71 × 10−4 m
C)17.4 × 10−3 m
D)5.53 × 10−4 m
E)2.90 × 10−4 m
A)4.36 × 10−4 m
B)8.71 × 10−4 m
C)17.4 × 10−3 m
D)5.53 × 10−4 m
E)2.90 × 10−4 m

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
12
The fundamental frequency of HF is 8.72 × 1013 Hz.The energy associated with a transition from the 10th to the 9th vibrational quantum number (in eV)is
A)3.61
B)0.361
C)0.060 5
D)0.605
E)0.182
A)3.61
B)0.361
C)0.060 5
D)0.605
E)0.182

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
13
The energy released when an atom takes an electron is called
A)internal energy
B)dissociation energy
C)binding energy
D)electron affinity
E)ionization energy
A)internal energy
B)dissociation energy
C)binding energy
D)electron affinity
E)ionization energy

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
14
The dissociation energy of the hydrogen molecule is approximately 5 eV.What is the temperature of a monatomic molecule whose kinetic energy is equal to 5.000 eV?
A)28990 K
B)57970 K
C)38650 K
D)23190 K
E)12880 K
A)28990 K
B)57970 K
C)38650 K
D)23190 K
E)12880 K

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
15
A diatomic molecule consists of two point masses,m1 and m2,separated by a distance r.If x is the distance from m1 to the center of mass,find the moment of inertia in terms of x about an axis perpendicular to the molecular axis through the center of mass.
A)0
B)m1m2 r2/m1 + m2
C)m1(r − x)2 + m2x2
D)m1x2 + m2(r − x)2
E)m2x2 + m1r2
A)0
B)m1m2 r2/m1 + m2
C)m1(r − x)2 + m2x2
D)m1x2 + m2(r − x)2
E)m2x2 + m1r2

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
16
A molecule makes a transition from the J = 1 to the J = 0 rotational energy state.The wavelength of the emitted photon is 2.6 × 10−3 m.What is the moment of inertia of the molecule (in kg ⋅ m2)?
A)2.9 × 10−46
B)5.7 × 10−45
C)1.1 × 10−44
D)1.5 × 10−46
E)9.1 × 10−46
A)2.9 × 10−46
B)5.7 × 10−45
C)1.1 × 10−44
D)1.5 × 10−46
E)9.1 × 10−46

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
17
The fundamental frequency of CO is 6.42 × 1013 Hz.If the atomic masses are 12 u and 16 u (1 u = 1.66 × 10−27 kg),find the force constant (in N/m)for the diatomic molecule.
A)970
B)1 530
C)1 850
D)480
E)47
A)970
B)1 530
C)1 850
D)480
E)47

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
18
A diatomic molecule consists of two point masses,m1 and m2,separated by a distance r.If x is the distance from m1 to the center of mass,find the moment of inertia in terms of x about an axis parallel to the molecular axis through the center of mass.
A)0
B)m1x2 + m2(r − x)2
C)m1m2 r2(m1m2)
D)m1(r − x)2 + m2x2
E)m1x2 + m2r2
A)0
B)m1x2 + m2(r − x)2
C)m1m2 r2(m1m2)
D)m1(r − x)2 + m2x2
E)m1x2 + m2r2

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
19
An oxygen molecule has a moment of inertia of 5 × 10−46 kg ⋅ m2.Calculate the bond length (in nm).Recall that the atomic mass of oxygen is 16 u (1 u = 1.66 × 10−27 kg).
A)0.3
B)0.1
C)0.2
D)0.4
E)0.5
A)0.3
B)0.1
C)0.2
D)0.4
E)0.5

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
20
Assume the angular momentum of a diatomic molecule is quantized according to the relation 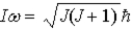
)What are the allowed rotational kinetic energies?
A)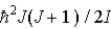
B)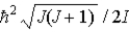
C)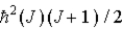
D)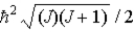
E)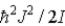
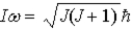
)What are the allowed rotational kinetic energies?
A)
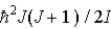
B)
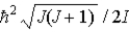
C)
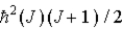
D)
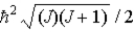
E)
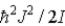

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
21
In comparing vibrational and rotational levels in molecules,we find that the energy separation between adjacent energy levels is
A)the same in rotational and vibrational levels.
B)greater in rotational than in vibrational levels.
C)greater in vibrational than in rotational levels.
D)directly proportional with one rotational level for each vibrational level.
E)inversely proportional with one rotational level for each vibrational level.
A)the same in rotational and vibrational levels.
B)greater in rotational than in vibrational levels.
C)greater in vibrational than in rotational levels.
D)directly proportional with one rotational level for each vibrational level.
E)inversely proportional with one rotational level for each vibrational level.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
22
The difference between donor and acceptor atoms in a doped semiconductor is that
A)the donor energy level lies halfway between the valence band and the acceptor level.
B)the donor energy level lies near the valence band and the acceptor energy level lies near the conduction band.
C)donor energy levels cannot exist unless acceptor energy levels are present.
D)the donor energy level lies near the conduction band and the acceptor energy level lies near the valence band.
E)the acceptor energy level lies halfway between the conduction band and the donor energy level.
A)the donor energy level lies halfway between the valence band and the acceptor level.
B)the donor energy level lies near the valence band and the acceptor energy level lies near the conduction band.
C)donor energy levels cannot exist unless acceptor energy levels are present.
D)the donor energy level lies near the conduction band and the acceptor energy level lies near the valence band.
E)the acceptor energy level lies halfway between the conduction band and the donor energy level.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
23
In the Lennard-Jones model of the hydrogen molecule,the potential is given by 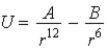
)In this model,the minimum internuclear separation,r0,is
A)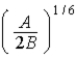 .
.
B)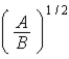 .
.
C)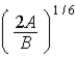 .
.
D)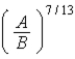 .
.
E)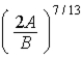 .
.
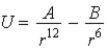
)In this model,the minimum internuclear separation,r0,is
A)
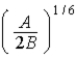 .
.B)
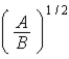 .
.C)
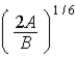 .
.D)
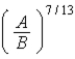 .
.E)
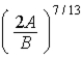 .
.
Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
24
When a molecule jumps from a rotational energy level characterized by the rotational quantum number J to one characterized by J − 1,the difference in energy of levels J and J − 1,EJ − EJ − 1,is
A)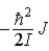 .
.
B)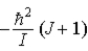 .
.
C)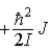 .
.
D)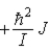 .
.
E)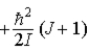 .
.
A)
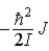 .
.B)
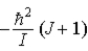 .
.C)
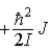 .
.D)
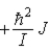 .
.E)
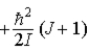 .
.
Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
25
The energy of a molecule can normally be divided into the following categories:
A)rotational and vibrational
B)translational,rotational and vibrational
C)electronic,translational,rotational,and vibrational
D)rotational
E)electronic
A)rotational and vibrational
B)translational,rotational and vibrational
C)electronic,translational,rotational,and vibrational
D)rotational
E)electronic

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
26
If an electric field is applied to a metal
A)very few electrons are excited into the conduction band.
B)electrons having energies near the Fermi energy require only a small amount of additional energy from the applied field to reach nearby empty energy states.
C)electrons having energies near the bottom of the band require only a small amount of additional energy from the applied field to reach nearby empty energy states.
D)the principal mode of conduction is through the motion of holes in the filled part of the band.
E)the Fermi energy Ef becomes equal to the applied electric field E.
A)very few electrons are excited into the conduction band.
B)electrons having energies near the Fermi energy require only a small amount of additional energy from the applied field to reach nearby empty energy states.
C)electrons having energies near the bottom of the band require only a small amount of additional energy from the applied field to reach nearby empty energy states.
D)the principal mode of conduction is through the motion of holes in the filled part of the band.
E)the Fermi energy Ef becomes equal to the applied electric field E.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
27
The wave functions of some molecules are a combination of wave functions with different values of the orbital quantum number 
)The wave function of PF5 combines s,p and d states in an sp3d hybrid orbital.We would expect such an overlap of wave functions in individual molecules to represent
A)ionic bonding
B)metallic bonding.
C)covalent bonding.
D)Van der Waal's bonding.
E)hydrogen bonding.
)The wave function of PF5 combines s,p and d states in an sp3d hybrid orbital.We would expect such an overlap of wave functions in individual molecules to represent
A)ionic bonding
B)metallic bonding.
C)covalent bonding.
D)Van der Waal's bonding.
E)hydrogen bonding.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
28
Because HF,hydrogen fluoride,is a covalent gaseous molecule at room temperature,we might reasonably expect that at room temperature HCl,hydrogen chloride,is
A)a covalent gaseous molecule.
B)a covalent solid.
C)a metallic gas.
D)a metallic solid.
E)an ionic solid.
A)a covalent gaseous molecule.
B)a covalent solid.
C)a metallic gas.
D)a metallic solid.
E)an ionic solid.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
29
When a voltage ΔV is applied to a p-n junction diode at absolute temperature T,the current voltage relationship is
A)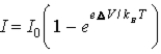 .
.
B)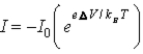 .
.
C)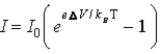 .
.
D)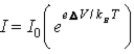 .
.
E)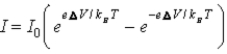 .
.
A)
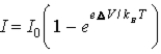 .
.B)
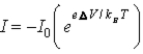 .
.C)
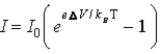 .
.D)
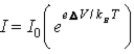 .
.E)
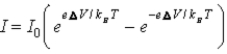 .
.
Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
30
When calculating the rotational kinetic energy of a diatomic molecule,with atoms of mass m1 and m2,the moment of inertia about an axis passing through the molecule's center of mass,with r the atomic separation,is
A)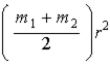 .
.
B)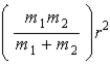 .
.
C)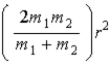 .
.
D)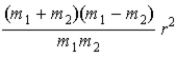 .
.
E)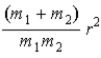 .
.
A)
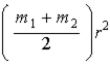 .
.B)
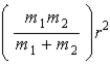 .
.C)
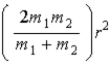 .
.D)
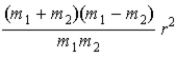 .
.E)
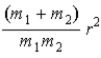 .
.
Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
31
The diagram below shows the distance between the nuclei,pA and pB,and the electrons,e1 and e2,in a hydrogen molecule.We would expect the electrostatic potential energy of this molecule to be 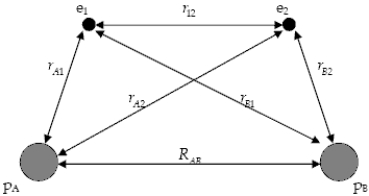
A)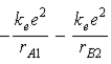 .
.
B)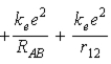 .
.
C)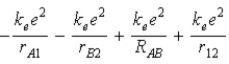 .
.
D)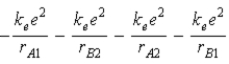 .
.
E)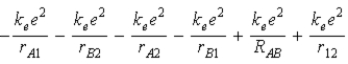 .
.

A)
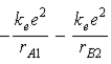 .
.B)
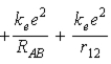 .
.C)
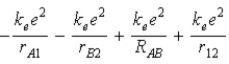 .
.D)
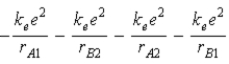 .
.E)
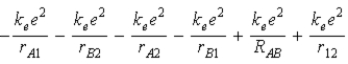 .
.
Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
32
The Fermi energy corresponds to
A)the maximum energy electrons can have in a metal at T = 0 K.
B)the maximum energy electrons can have in a metal at T = 0 C.
C)the minimum energy electrons can have in a metal at T = 0 K.
D)the number of electrons per unit volume between E and E + dE.
E)the minimum energy electrons can have in a metal at T = 0 C.
A)the maximum energy electrons can have in a metal at T = 0 K.
B)the maximum energy electrons can have in a metal at T = 0 C.
C)the minimum energy electrons can have in a metal at T = 0 K.
D)the number of electrons per unit volume between E and E + dE.
E)the minimum energy electrons can have in a metal at T = 0 C.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
33
The Fermi energy of a metal at a temperature T is 7.0 eV.What is the average energy (in eV)of a conduction electron at that temperature?
A)2.8
B)7.0
C)3.5
D)4.2
E)4.7
A)2.8
B)7.0
C)3.5
D)4.2
E)4.7

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
34
To find the number of electrons per unit volume with energy between E and E + dE in a metal we must multiply the number of allowed states per unit volume with energy E by
A)the probability that a state is unoccupied,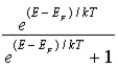 .
.
B)the probability that a state is occupied,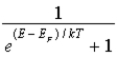 .
.
C)the probability that a state is unoccupied,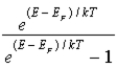 .
.
D)the probability that a state is occupied,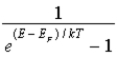 .
.
E)dE alone.
A)the probability that a state is unoccupied,
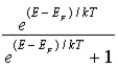 .
.B)the probability that a state is occupied,
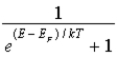 .
.C)the probability that a state is unoccupied,
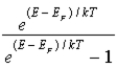 .
.D)the probability that a state is occupied,
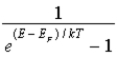 .
.E)dE alone.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
35
The Fermi temperature is
A)a characteristic temperature of an electron gas at a physical temperature of absolute zero.
B)a characteristic temperature of an electron gas at a physical temperature of 0° Celsius.
C)the temperature of the electron gas in absolute degrees.
D)related to the Fermi energy by the relation EF = (3/2)kT.
E)independent of the Fermi energy.
A)a characteristic temperature of an electron gas at a physical temperature of absolute zero.
B)a characteristic temperature of an electron gas at a physical temperature of 0° Celsius.
C)the temperature of the electron gas in absolute degrees.
D)related to the Fermi energy by the relation EF = (3/2)kT.
E)independent of the Fermi energy.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
36
The Fermi temperature of copper is 80 000 K.The corresponding Fermi energy (in eV)is
A)7
B)5
C)3
D)1
E)4
A)7
B)5
C)3
D)1
E)4

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
37
The energy gap for germanium is 0.670 eV at room temperature.What wavelength must a photon have (in nm)to excite the electron to the conduction band?
A)640
B)1 090
C)1 850
D)2 200
E)925
A)640
B)1 090
C)1 850
D)2 200
E)925

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
38
When a molecule jumps from a rotational energy level characterized by the rotational quantum number J to one characterized by J + 1,the change in energy,EJ + 1 − EJ,is
A)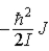 .
.
B)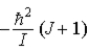 .
.
C)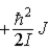 .
.
D)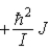 .
.
E)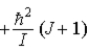 .
.
A)
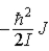 .
.B)
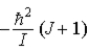 .
.C)
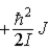 .
.D)
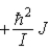 .
.E)
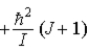 .
.
Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
39
An energy band in a solid consists of
A)an infinite number of levels,with each level corresponding to a point in a box.
B)a large number of energy levels so closely spaced that they may be regarded as a continuous band.
C)an infinite number of wave functions,with each wave function corresponding to a point in a box.
D)a large number of electrons so closely spaced that they may be regarded as a continuous band of electric charge.
E)an infinite number of electrons,with each electron corresponding to a point in a box.
A)an infinite number of levels,with each level corresponding to a point in a box.
B)a large number of energy levels so closely spaced that they may be regarded as a continuous band.
C)an infinite number of wave functions,with each wave function corresponding to a point in a box.
D)a large number of electrons so closely spaced that they may be regarded as a continuous band of electric charge.
E)an infinite number of electrons,with each electron corresponding to a point in a box.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
40
Ellis and Randy are looking at a molecular absorption spectrum.The spectral lines appear to fall into two groups with a gap in the middle.Ellis says that this must be an absorption spectrum for transitions between the v = 0 and v = 1 vibrational states of a diatomic molecule.Randy says the gap in the middle must occur because a ΔJ = 0 transition is forbidden.Which one,if either,is correct,and why?
A)Ellis,because rotational levels are separated by greater energy differences than vibrational levels.
B)Randy,because rotational levels are separated by greater energy differences than vibrational levels.
C)Ellis,because the ΔJ = 0 transition is the most prominent spectral line in transitions between vibrational levels.
D)Neither,because rotational levels are separated by greater energies that vibrational levels and ΔJ = 0 transitions are not forbidden.
E)Both,because vibrational levels are separated by greater energy differences than rotational levels and ΔJ = 0 transitions are forbidden.
A)Ellis,because rotational levels are separated by greater energy differences than vibrational levels.
B)Randy,because rotational levels are separated by greater energy differences than vibrational levels.
C)Ellis,because the ΔJ = 0 transition is the most prominent spectral line in transitions between vibrational levels.
D)Neither,because rotational levels are separated by greater energies that vibrational levels and ΔJ = 0 transitions are not forbidden.
E)Both,because vibrational levels are separated by greater energy differences than rotational levels and ΔJ = 0 transitions are forbidden.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
41
The energy gap for a semiconductor is 1.25 eV.Of the frequencies given below,what is the minimum frequency photon than can move an electron from the valence band to the conduction band?
A)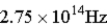
B)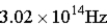
C)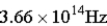
D)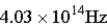
E)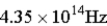
A)
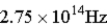
B)
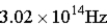
C)
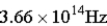
D)
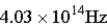
E)
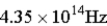

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
42
Solid argon has a density of 1650 kg/m3.The atomic weight of argon is 40.0.Assuming each atom occupies a cubical volume,what is the distance between the argon atoms?

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
43
An LED emits light of wavelength 600 nm.What is its band gap?
A)1.11 eV
B)1.54 eV
C)1.99 eV
D)2.07 eV
E)2.33 eV
A)1.11 eV
B)1.54 eV
C)1.99 eV
D)2.07 eV
E)2.33 eV

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
44
In the hydrogen molecule,H2,the separation between the protons is 10−10 m.If the molecule is in its first rotational energy state,what is the angular velocity of the molecule about its center of mass?

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
45
What is the energy of the first rotational state of the hydrogen (H2)molecule? The separation between the protons is 10−10 m and the mass of each proton is 1.67 × 10−27 kg.(h = 6.626 × 10−34 J ⋅ s and 1 eV = 1.6 × 10−19 J. )

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck
46
The smallest object one can distinguish using the electron microscope is on the order of one nanometer (1 nm = 10−9 m).How many atoms of gold are contained in a cube whose edge is 1 nm long? The atomic mass of gold is 197 and its density is 19.3 g/cm3.

Unlock Deck
Unlock for access to all 46 flashcards in this deck.
Unlock Deck
k this deck


