Deck 12: Chi-Square Tests

Question 1

A goodness-of-fit test analyzes for two qualitative variables whereas a chi-square test of a contingency table is for a single qualitative variable.

Answer 1

False

Question 2

For the chi-square test of a contingency table, the expected cell frequencies are found as ________.

A) the row total multiplied by the column total divided by the sample size
B) the observed cell frequency
C) (r−1)(c−1)
D) rc

Answer 2

the row total multiplied by the column total divided by the sample size

Question 3

For the Jarque-Bera test for normality, the test statistic is assumed to have a chi-square distribution with two degrees of freedom.

Answer 3

True

Question 4

The chi-square test of a contingency table is a test of independence for ________.

A) a single qualitative variable
B) two qualitative variables
C) two quantitative variables
D) three or more quantitative variables

Question 5

The chi-square goodness-of-fit test is a right-tailed test.

Question 6

For the goodness-of-fit test, the chi-square test statistic will ________.

A) always equal zero
B) always be negative
C) be at least zero
D) always be equal to n

Question 7

For the goodness-of-fit test, the expected category frequencies are found using the ________.

A) sample proportions
B) proportions specified under the null hypothesis
C) average of the hypothesized and sample proportions
D) proportions specified under the alternative hypothesis

Question 8

For a multinomial experiment with k categories, the goodness-of-fit test statistic is assumed to follow a chi-square distribution with k degrees of freedom.

Question 9

Which of the following null hypotheses is used to test if five population proportions are the same?

A) H₀: p₁ = p₂ = p₃ = p₄ = p₅ = 0.25
B) H₀: p₁ = p₂ = p₃ = p₄ = 0.25
C) H₀: p₁ = p₂ = p₃ = p₄ = 0.20
D) H₀: p₁ = p₂ = p₃ = p₄ = p₅ = 0.20

Question 10

For a multinomial experiment, which of the following is not true?

A) The number of categories is at least two, k ≥ 2.
B) The trials are dependent.
C) The sum of the cell probabilities is P₁ + P₂ + ... + P_k = 1.
D) The category probabilities are the same for each trial.

Question 11

When applying the goodness-of-fit test for normality, the data are divided into k non-overlapping intervals.

Question 12

What are the degrees of freedom for the goodness-of-fit test for normality?

A) 2
B) k − 3
C) k − 2
D) k − 1

Question 13

The chi-square test statistic measures the difference between the observed frequencies and the expected frequencies assuming the null hypothesis is true.

Question 14

For the chi-square test of a contingency table, the expected cell frequencies are found as e_{ij =} which is the same as ________.

A) the observed cell frequencies
B) the cell probability multiplied by the sample size
C) the row total
D) the column total

Question 15

For a chi-square test of a contingency table, each expected frequency must be at least 3.

Question 16

The chi-square test of a contingency table is valid when the expected cell frequencies are ________.

A) equal to 0
B) more than 0 but less than 5
C) at least 5
D) negative

Question 17

For the goodness-of-fit test, the sum of the expected frequencies must equal ________.

A) 1
B) n
C) k
D) k−1

Question 18

For a chi-square test of a contingency table, the expected frequencies for each cell are calculated assuming the two events are independent of one another.

Question 19

If the null hypothesis is rejected by the goodness-of-fit test, the alternative hypothesis specifies which of the population proportions differ from their hypothesized values.

Question 20

For a chi-square test of a contingency table, the degrees of freedom are calculated as (r−1)(c−1) where r and c are the number of rows and columns in the contingency table.

Question 21

Suppose you want to determine if gender and major are independent. Which of the following tests should you use?

A) Goodness-of-fit test for a multinomial experiment
B) Chi-square test for independence
C) Goodness-of-fit test for normality
D) Jarque-Bera test for normality

Question 22

For the chi-square test for normality, the expected frequencies for each interval must be ________.

A) exactly 2
B) k − 3
C) at least 5
D) k − 1

Question 23

Packaged candies have three different types of colors. Suppose you want to determine if the population proportion of each color is the same. The most appropriate test is the ________.

A) goodness-of-fit test for a multinomial experiment
B) chi-square test for independence
C) goodness-of-fit test for normality
D) Jarque-Bera test for normality

Question 24

A card-dealing machine deals spades (1), hearts (2), clubs (3), and diamonds (4) at random as if from an infinite deck. In a randomness check, 1,600 cards were dealt and counted. The results are shown below. 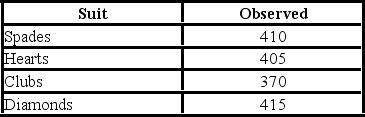The p-value is ________.

A) less than 0.01
B) between 0.01 and 0.05
C) between 0.05 and 0.10
D) greater than 0.10

Question 25

A university has six colleges and takes a poll to gauge student support for a tuition increase. The university wants to ensure each college is represented fairly. The below table shows the observed number of students who participate in the poll from each college and the actual proportion of students in each college. 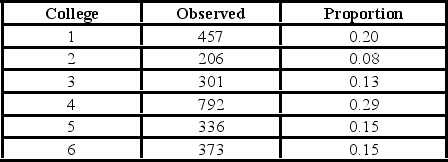For the goodness-of-fit test, the alternative hypothesis states that ________.

A) H_A: Not all population proportions are equal to 0,20
B) H_A: At least one of the population proportions is different from its hypothesized value
C) H_A: Not all population proportions are the same
D) H_A: Not all population proportions are equal to 0.15

Question 26

A university has six colleges and takes a poll to gauge student support for a tuition increase. The university wants to ensure each college is represented fairly. The below table shows the observed number of students who participate in the poll from each college and the actual proportion of students in each college. 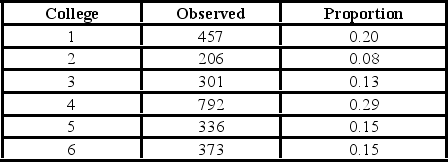For the goodness-of-fit test, the assumed degrees of freedom are ________.

A) 2
B) 3
C) 4
D) 5

Question 27

For the goodness-of-fit test for normality to be applied, what is the minimum number of qualitative intervals the quantitative data can be converted to?

A) 2
B) 4
C) 5
D) 10

Question 28

The calculation of the Jarque-Bera test statistic involves ________.

A) only the sample size
B) the sample size, standard deviation, and average
C) the sample size, skewness coefficient, and kurtosis coefficient
D) the sample average, skewness coefficient, and kurtosis coefficient

Question 29

A card-dealing machine deals spades (1), hearts (2), clubs (3), and diamonds (4) at random as if from an infinite deck. In a randomness check, 1,600 cards were dealt and counted. The results are shown below. 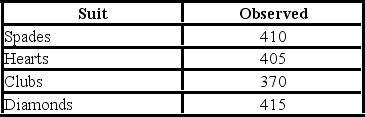For the goodness-of-fit test, the degrees of freedom are ________.

A) 2
B) 3
C) 4
D) 5

Question 30

A university has six colleges and takes a poll to gauge student support for a tuition increase. The university wants to ensure each college is represented fairly. The below table shows the observed number of students who participate in the poll from each college and the actual proportion of students in each college. 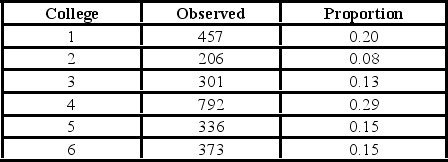Which of the following is the value of the goodness-of-fit test statistic?

A) 3.08
B) 15.09
C) 15.64
D) 16.75

Question 31

A card-dealing machine deals spades (1), hearts (2), clubs (3), and diamonds (4) at random as if from an infinite deck. In a randomness check, 1,600 cards were dealt and counted. The results are shown below. 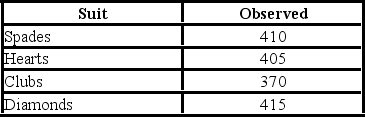Using the p-value approach and α = 0.05, the decision and conclusion are ________.

A) do not reject the null hypothesis; all of the population proportions are the same
B) reject the null hypothesis; conclude that not all proportions are equal to 0.20
C) reject the null hypothesis; conclude that not all proportions are equal to 0.25
D) do not reject the null hypothesis; we cannot conclude that not all of the proportions are equal to 0.25

Question 32

If a test statistic has a value of X and is assumed to be χ² distributed with df degrees of freedom, then the p-value for a right-tailed test found by using Excel's command ________.

A) '=CHISQ.DIST.RT(X, Deg_freedom)'
B) '=CHISQ.DIST.RT(Deg_freedom, X)'
C) '=1-CHISQ.DIST.RT(X, Deg_freedom)'
D) '=1-CHISQ.DIST.RT(Deg_freedom, X)'

Question 33

For the goodness-of-fit test for normality, the null and alternative hypotheses are ________.

A) H₀: Data does not follow a normal distribution, H_A: Data follows a normal distribution
B) H₀: Data follows a normal distribution, H_A: Data does not follow a normal distribution
C) H₀: Data follows a normal distribution, H_A: Data are skewed right
D) H₀: Data follows a normal distribution, H_A: Data are skewed left

Question 34

A card-dealing machine deals spades (1), hearts (2), clubs (3), and diamonds (4) at random as if from an infinite deck. In a randomness check, 1,600 cards were dealt and counted. The results are shown below. 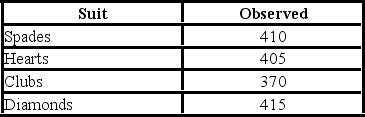To test if the poker-dealing machine deals cards at random, the null and alternative hypotheses are ________.

A) H₀: p₁ = p₂ = p₃ = p₄ = 0, H_A: Not all population proportions are equal to 0,25
B) H₀: p₁ = p₂ = p₃ = p₄ = 0.25, H_A: Not all population proportions are equal to 0,25
C) H₀: p₁ = p₂ = p₃ = p₄ = 1, H_A: Not all population proportions are equal to 0,25
D) H₀: p₁ = p₂ = p₃ = p₄ = 0.20, H_A: Not all population proportions are equal to 0,20

Question 35

A card-dealing machine deals spades (1), hearts (2), clubs (3), and diamonds (4) at random as if from an infinite deck. In a randomness check, 1,600 cards were dealt and counted. The results are shown below. 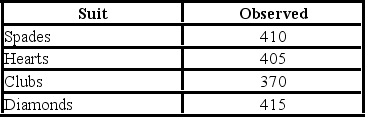Using the critical value approach, the decision and conclusion are ________.

A) do not reject the null hypothesis; we cannot conclude that not all of the proportions are equal to 0.25
B) do not reject the null hypothesis; all of the population proportions are the same
C) reject the null hypothesis; conclude that not all proportions are equal to 0.25
D) reject the null hypothesis; conclude that not all proportions are equal to 0.20

Question 36

Suppose you want to determine if the quarterly returns for mutual funds have a normal distribution using the skewness and kurtosis coefficients. The most appropriate test is the ________.

A) goodness-of-fit test for a multinomial experiment
B) chi-square test for independence
C) goodness-of-fit test for normality
D) Jarque-Bera test for normality

Question 37

Suppose you want to determine if the quarterly returns for mutual funds have a normal distribution when your available data is partitioned into some non-overlapping. The most appropriate test is the ________.

A) goodness-of-fit test for a multinomial experiment
B) chi-square test for independence
C) goodness-of-fit test for normality
D) Jarque-Bera test for normality

Question 38

A card-dealing machine deals spades (1), hearts (2), clubs (3), and diamonds (4) at random as if from an infinite deck. In a randomness check, 1,600 cards were dealt and counted. The results are shown below. 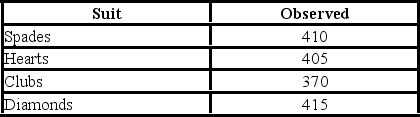At the 5% significance level, the critical value is ________.

A) 6.251
B) 7.815
C) 9.348
D) 11.345

Question 39

For the Jarque-Bera test for normality, the null and alternative hypotheses are ________.

A) H₀: S < 0 and K > 0, H_A: S < 0 or K < 0
B) H₀: S < 0 and K = 0, H_A: S > 0 or K ≠ 0
C) H₀: S = 0 and K = 0, H_A: S ≠ 0 or K ≠ 0
D) H₀: S = 0 and K > 0, H_A: S ≠ 0 or K < 0

Question 40

A card-dealing machine deals spades (1), hearts (2), clubs (3), and diamonds (4) at random as if from an infinite deck. In a randomness check, 1,600 cards were dealt and counted. The results are shown below. 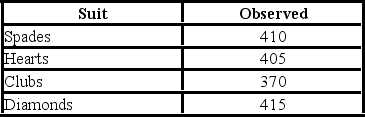For the goodness-of-fit test, the value of the test statistic is ________.

A) 2.25
B) 3.125
C) 6.45
D) 7.815

Question 41

A university has six colleges and takes a poll to gauge student support for a tuition increase. The university wants to ensure each college is represented fairly. The below table shows the observed number of students who participate in the poll from each college and the actual proportion of students in each college. 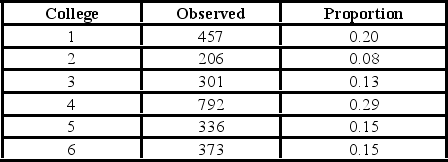Using the p-value approach and α = 0.01, the decision and conclusion are ________.

A) do not reject the null hypothesis; all proportions are equal to 0.20
B) do not reject the null hypothesis; we cannot conclude that not all of the proportions are the same
C) reject the null hypothesis; at least one of the proportions is different from its hypothesized value
D) reject the null hypothesis; all of the proportions are not the same

Question 42

A fund manager wants to know if it is equally likely that the Dow Jones Industrial Average will go up each day of the week. For each day of the week, the fund manager observes the following number of days when the Dow Jones Industrial Average goes up. 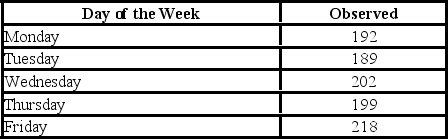For the goodness-of-fit test, the null and alternative hypotheses are ________.

A) H₀: p₁ = p₂ = p₃ = p₄ = 1/4, H_A: Not all population proportions are equal to 1/4
B) H₀: p₁ = p₂ = p₃ = p₄ = p₅ = 1/5, H_A: Not all population proportions are equal to 1/5
C) H₀: p₁ = p₂ = p₃ = p₄ = p₅ = 1/4, H_A: Not all population proportions are equal to 1/4
D) H₀: p₁ = p₂ = p₃ = p₄ = 1/5, H_A: Not all population proportions are equal to 1/5

Question 43

A university has six colleges and takes a poll to gauge student support for a tuition increase. The university wants to ensure each college is represented fairly. The below table shows the observed number of students that participate in the poll from each college and the actual proportion of students in each college. 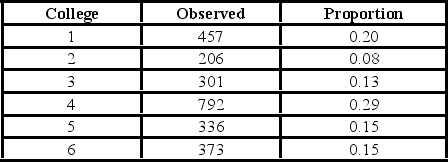Using the critical value approach, the decision and conclusion are ________.

A) reject the null hypothesis; at least one of the proportions is different from its hypothesized value
B) reject the null hypothesis; all of the proportions are not the same
C) do not reject the null hypothesis; all proportions are equal to 0.20
D) do not reject the null hypothesis; we cannot conclude not all of the proportions are the same

Question 44

A university has six colleges and takes a poll to gauge student support for a tuition increase. The university wants to ensure each college is represented fairly. The below table shows the observed number of students who participate in the poll from each college and the actual proportion of students in each college. 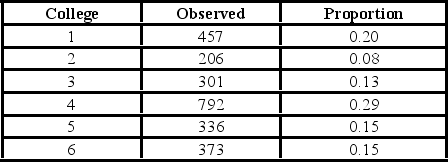The p-value is ________.

A) less than 0.01
B) between 0.01 and 0.05
C) between 0.05 and 0.10
D) greater than 0.10

Question 45

A fund manager wants to know if it is equally likely that the Dow Jones Industrial Average will go up each day of the week. For each day of the week, the fund manager observes the following number of days when the Dow Jones Industrial Average goes up. 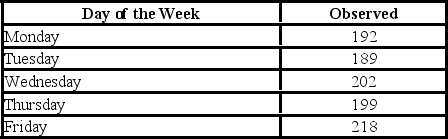The p-value is ________.

A) less than 0.01
B) between 0.01 and 0.05
C) between 0.05 and 0.10
D) greater than 0.10

Question 46

In the following table, likely voters' preferences of two candidates are cross-classified by gender. For the chi-square test of independence, the value of the test statistic is ________.

A) 2.34
B) 1.62
C) 3.25
D) 4

Question 47

A fund manager wants to know if it is equally likely that the Dow Jones Industrial Average will go up each day of the week. For each day of the week, the fund manager observes the following number of days when the Dow Jones Industrial Average goes up. 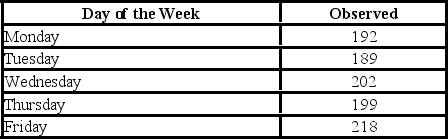For the goodness-of-fit test, what are the degrees of freedom for the chi-squared test statistic?

A) 4
B) 5
C) 6
D) 7

Question 48

In the following table, likely voters' preferences of two candidates are cross-classified by gender. For the chi-square test of independence, the assumed degrees of freedom are ________.

A) 1
B) 2
C) 3
D) 4

Question 49

A fund manager wants to know if it is equally likely that the Dow Jones Industrial Average will go up each day of the week. For each day of the week, the fund manager observes the following number of days when the Dow Jones Industrial Average goes up. 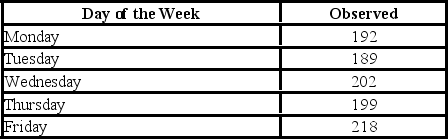Using the critical value approach, the decision and conclusion are

A) reject the null hypothesis; not all of the proportions are the same
B) reject the null hypothesis; all of the proportions are not the same
C) do not reject the null hypothesis; all of the proportions are the same
D) do not reject the null hypothesis; we cannot conclude that not all of the proportions are the same

Question 50

In the following table, individuals are cross-classified by their age group and income level. 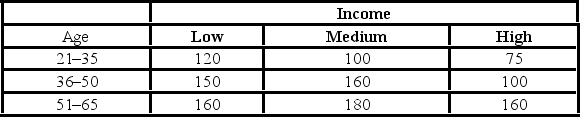Which of the following is the estimated joint probability for the "low income and 21-35 age group" cell?

A) 0.0830
B) 0.0874
C) 0.0996
D) 0.1328

Question 51

A fund manager wants to know if it is equally likely that the Dow Jones Industrial Average will go up each day of the week. For each day of the week, the fund manager observes the following number of days when the Dow Jones Industrial Average goes up. 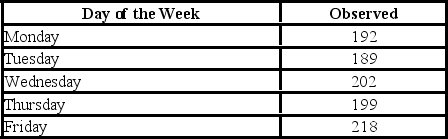At the 5% significance level, the critical value is ________.

A) 7.779
B) 9.488
C) 11.143
D) 13.277

Question 52

In the following table, likely voters' preferences of two candidates are cross-classified by gender. Using the p-value approach and α = 0.10, the decision and conclusion are ________.

A) reject the null hypothesis; gender and candidate preference are dependent
B) do not reject the null hypothesis; gender and candidate preference are independent
C) reject the null hypothesis; gender and candidate preference are independent
D) do not reject null hypothesis; gender and candidate preference are dependent

Question 53

In the following table, likely voters' preferences of two candidates are cross-classified by gender. The p-value is ________.

A) less than 0.01
B) between 0.01 and 0.05
C) between 0.05 and 0.10
D) greater than 0.10

Question 54

In the following table, likely voters' preferences of two candidates are cross-classified by gender. At the 10% significance level, the critical value is ________.

A) 6.635
B) 5.024
C) 3.841
D) 2.706

Question 55

In the following table, likely voters' preferences of two candidates are cross-classified by gender. Using the critical value approach, the decision and conclusion are ________.

A) reject the null hypothesis; gender and candidate preference are dependent
B) do not reject the null hypothesis; gender and candidate preference are independent
C) reject the null hypothesis; gender and candidate preference are independent
D) do not reject the null hypothesis; gender and candidate preference are dependent

Question 56

A fund manager wants to know if it is equally likely that the Dow Jones Industrial Average will go up each day of the week. For each day of the week, the fund manager observes the following number of days when the Dow Jones Industrial Average goes up. 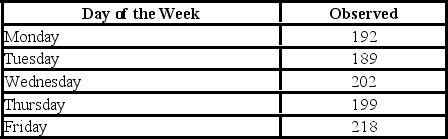Using the p-value approach and α = 0.05, the decision and conclusion are ________.

A) do not reject the null hypothesis; all of the proportions are the same
B) do not reject the null hypothesis; we cannot conclude that not all of the proportions are the same
C) reject the null hypothesis; not all of the proportions are the same
D) reject the null hypothesis; all of the proportions are not the same

Question 57

In the following table, likely voters' preferences of two candidates are cross-classified by gender. To test that gender and candidate preference are independent, the null hypothesis is ________.

A) H₀: Gender and candidate preference are independent
B) H₀: Gender and candidate preference are mutually exclusive
C) H₀: Gender and candidate preference are not mutually exclusive
D) H₀: Gender and candidate preference are dependent

Question 58

In the following table, individuals are cross-classified by their age group and income level. 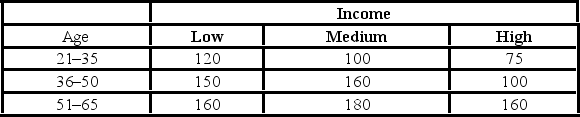Which of the following is the expected joint probability for the "low income and 21-35 age group" cell assuming age group and income are independent?

A) 0.0830
B) 0.0874
C) 0.0996
D) 0.1328

Question 59

A fund manager wants to know if it is equally likely that the Dow Jones Industrial Average will go up each day of the week. For each day of the week, the fund manager observes the following number of days when the Dow Jones Industrial Average goes up. 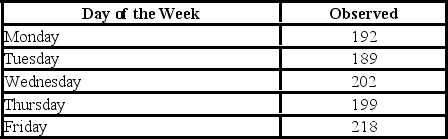Which of the following is the value of goodness-of-fit chi-square test statistic?

A) 0.605
B) 0.632
C) 1.62
D) 2.57

Question 60

A university has six colleges and takes a poll to gauge student support for a tuition increase. The university wants to ensure each college is represented fairly. The below table shows the observed number of students who participate in the poll from each college and the actual proportion of students in each college. 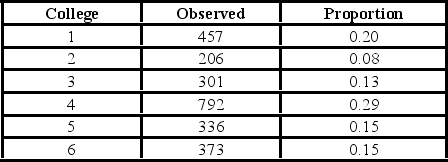At the 1% significance level, the critical value is ________.

A) 9.236
B) 11.070
C) 12.833
D) 15.086

Question 61

In the following table, individuals are cross-classified by their age group and income level. 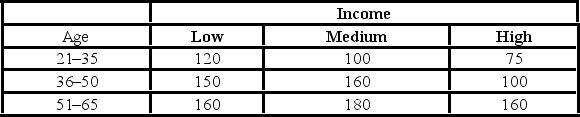Using the p-value approach and α = 0.05, the decision and conclusion are ________.

A) do not reject the null hypothesis; age and income are dependent
B) do not reject the null hypothesis; age and income are independent
C) reject the null hypothesis; age and income are dependent
D) reject the null hypothesis; age and income are independent

Question 62

The following table shows the distribution of employees in an organization. Martha Foreman, an analyst, wants to see if race has a bearing on the position a person holds with this company. 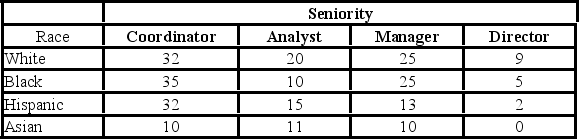Using the p-value approach and α = 0.05, the decision and conclusion are ________.

A) reject the null hypothesis; conclude race and seniority are dependent
B) reject the null hypothesis; conclude race and seniority are independent
C) do not reject the null hypothesis; cannot conclude race and seniority are dependent
D) do not reject the null hypothesis; conclude race and seniority are independent

Question 63

In the following table, individuals are cross-classified by their age group and income level. 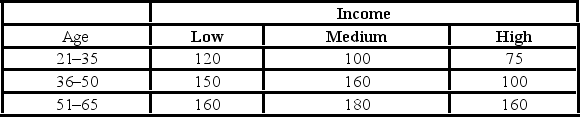To test that age group and income are independent, the null and alternative hypothesis are ________.

A) H₀: Age group and income are dependent; H_A: Age group and income are independent
B) H₀: Age group and income are mutually exclusive; H_A: Age group and income are not mutually exclusive
C) H₀: Age group and income are not mutually exclusive; H_A: Age group and income are mutually exclusive
D) H₀: Age group and income are independent; H_A: Age group and income are dependent

Question 64

The following table shows the distribution of employees in an organization. Martha Foreman, an analyst, wants to see if race has a bearing on the position a person holds with this company. 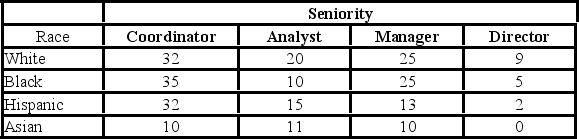For the chi-square test of independence, the value of the test statistic is ________.

A) 12.221
B) 15.378
C) 17.853
D) 20.154

Question 65

The following table shows the distribution of employees in an organization. Martha Foreman, an analyst, wants to see if race has a bearing on the position a person holds with this company. 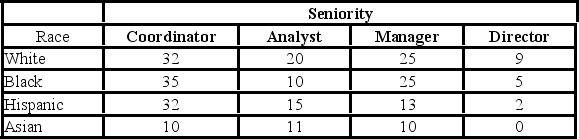To test that race and seniority are independent, the null and alternative hypothesis are ________.

A) H₀: Race and seniority are independent; H_A: Race and seniority are dependent
B) H₀: Race and seniority are mutually exclusive; H_A: Race and seniority are not mutually exclusive
C) H₀: Race and seniority are not mutually exclusive; H_A: Race and seniority are mutually exclusive
D) H₀: Race and seniority are dependent; H_A: Race and seniority are independent

Question 66

In the following table, individuals are cross-classified by their age group and income level. 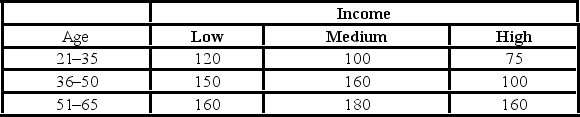For the chi-square test of independence, the degrees of freedom are ________.

A) 2
B) 4
C) 9
D) 8

Question 67

The following table shows the distribution of employees in an organization. Martha Foreman, an analyst, wants to see if race has a bearing on the position a person holds with this company. 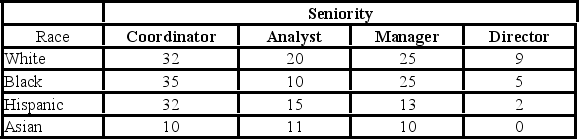Using the critical value approach, the decision and conclusion are ________.

A) reject the hypothesis; conclude race and seniority are dependent
B) reject the null hypothesis; conclude race and seniority are independent
C) do not reject the null hypothesis; conclude race and seniority are dependent
D) do not reject the null hypothesis; conclude race and seniority are independent

Question 68

In the following table, individuals are cross-classified by their age group and income level. 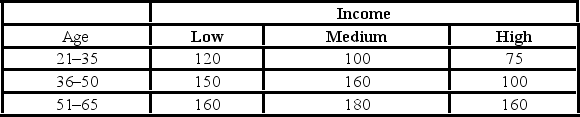Using the critical value approach, the decision and conclusion are ________.

A) do not reject the null hypothesis; age and income are dependent
B) do not reject the null hypothesis; age and income are independent
C) reject the null hypothesis; age and income are dependent
D) reject the null hypothesis; age and income are independent

Question 69

The heights (in cm) for a random sample of 60 males were measured. The sample mean is 166.55, the standard deviation is 12.57, the sample kurtosis is 0.12, and the sample skewness is −0.23. The following table shows the heights subdivided into non-overlapping intervals. 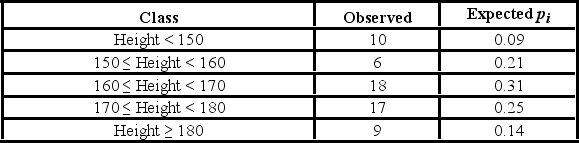For the goodness-of-fit test for normality, the null and alternative hypothesis are ________.

A) H₀: Heights follow a normal distribution with mean 166.55 and standard deviation 12.46, H_A: Heights do not follow a normal distribution with mean 166.55 and standard deviation 12.46
B) H₀: Heights do not follow a normal distribution with mean 166.55 and standard deviation 12.46, H_A: Heights follow a normal distribution with mean 166.55 and standard deviation 12.46
C) H₀: Heights follow a normal distribution with mean 166.55 and standard deviation 12.57, H_A: Heights do not follow a normal distribution with mean 166.55 and standard deviation 12.57
D) H₀: Heights do not follow a normal distribution with mean 166.55 and standard deviation 12.57, H_A: Heights follow a normal distribution with mean 166.55 and standard deviation 12.57

Question 70

In the following table, individuals are cross-classified by their age group and income level. 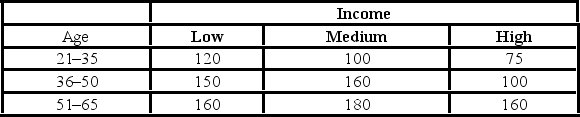Assuming age group and income are independent, the expected "low income and 21-35 age group" cell frequency is ________.

A) 105.27
B) 107.72
C) 146.31
D) 178.42

Question 71

The following table shows the distribution of employees in an organization. Martha Foreman, an analyst, wants to see if race has a bearing on the position a person holds with this company. 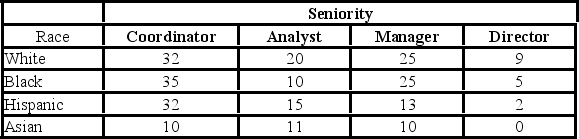The row total for Asians is ________.

A) 86
B) 75
C) 62
D) 31

Question 72

The following table shows the distribution of employees in an organization. Martha Foreman, an analyst, wants to see if race has a bearing on the position a person holds with this company. 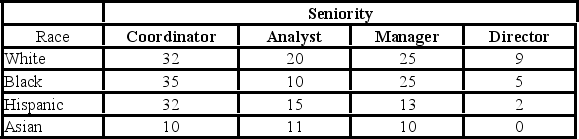The p-value is ________.

A) less than 0.01
B) between 0.01 and 0.05
C) between 0.05 and 0.10
D) greater than 0.10

Question 73

In the following table, individuals are cross-classified by their age group and income level. 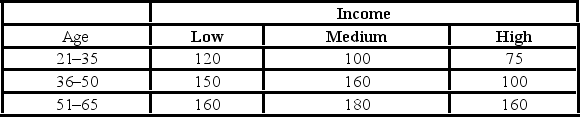At the 5% significance level, the critical value is ________.

A) 13.277
B) 11.143
C) 9.488
D) 7.779

Question 74

The following table shows the distribution of employees in an organization. Martha Foreman, an analyst, wants to see if race has a bearing on the position a person holds with this company. 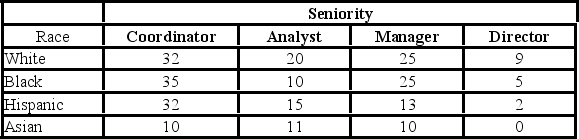At the 5% significance level, the critical value is ________.

A) 14.684
B) 16.919
C) 19.023
D) 21.666

Question 75

In the following table, individuals are cross-classified by their age group and income level. 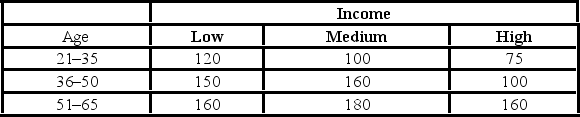For the chi-square test of independence, the value of the test statistic is ________.

A) 8.779
B) 10.840
C) 13.243
D) 16.159

Question 76

The heights (in cm) for a random sample of 60 males were measured. The sample mean is 166.55, the standard deviation is 12.57, the sample kurtosis is 0.12, and the sample skewness is −0.23. The following table shows the heights subdivided into non-overlapping intervals. 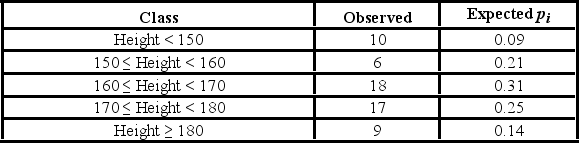The heights are subdivided into five intervals. The degrees of freedom for the goodness-of-fit test for normality is ________.

A) 2
B) 3
C) 4
D) 5

Question 77

In the following table, individuals are cross-classified by their age group and income level. The p-value is

A) Less than 0.01
B) Between 0.01 and 0.05
C) Between 0.05 and 0.10
D) Greater than 0.10

Question 78

The following table shows the distribution of employees in an organization. Martha Foreman, an analyst, wants to see if race has a bearing on the position a person holds with this company. 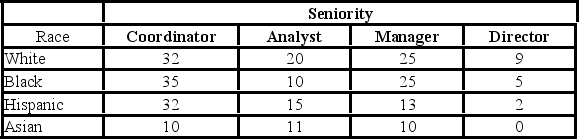The column total for directors is ________.

A) 16
B) 56
C) 73
D) 109

Question 79

The following table shows the distribution of employees in an organization. Martha Foreman, an analyst, wants to see if race has a bearing on the position a person holds with this company. 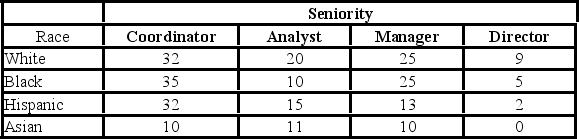Assuming that race and seniority are independent, which of the following is the expected frequency of Asian directors?

A) 0
B) 1.95
C) 3.91
D) 5.42

Question 80

The following table shows the distribution of employees in an organization. Martha Foreman, an analyst, wants to see if race has a bearing on the position a person holds with this company. 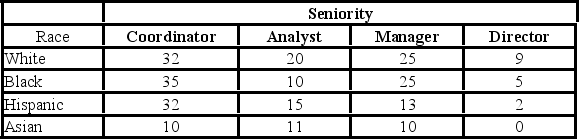For the chi-square test for independence, the degrees of freedom used are ________.

A) 2
B) 16
C) 9
D) 8