Deck 5: Probability: Review of Basic Concepts

Question 1

Which of the following is not an approach to assigning probabilities?

A) The Classical approach
B) The Trial and error approach
C) The Relative frequency approach
D) The Subjective approach
E) All of the above are approaches to assigning probabilities.

Answer 1

The Trial and error approach

Question 2

If the probability of an event is x,with $0 \leq x \leq 1$ ,then the odds in favor of the event are x to (1 - x).

Answer 2

True

Question 3

When events are mutually exclusive,two or more of them can happen at the same time.

Answer 3

False

Question 4

An experiment is an activity of measurement that results in an outcome.

Question 5

Bayes' theorem is an extension of the concept of conditional probability.

Question 6

Uncertainty plays an important role in our daily lives and activities as well as in business.

Question 7

When the events within a set are both mutually exclusive and exhaustive,the sum of their probabilities is 1.0.

Question 8

Sometimes it is useful to revise a probability on the basis of additional information that we didn't have before.

Question 9

Prior probability is a marginal probability while posterior probability is a conditional probability.

Question 10

The classical approach describes a probability:

A) in terms of the proportion of times an event is observed to occur in a very large number of trials.
B) in terms of the degree to which one happens to believe that an event will happen.
C) in terms of the proportion of times that an event can be theoretically expected to occur.
D) is dependent on the law of large numbers.
E) describes an event for which all outcomes are equally likely.

Question 11

If the event of interest is A,then:

A) the probability that A will not occur is [1 - P(A)].
B) the probability that A will not occur is the complement of A.
C) the probability is zero if event A is impossible.
D) the probability is one if event A is certain.
E) All of these are true.

Question 12

An example of the classical approach to probability would be:

A) the estimate of number of defective parts based on previous production data.
B) your estimate of the probability of a pop quiz in class on a given day.
C) the annual estimate of the number of deaths of persons age 25.
D) the probability of drawing an Ace from a deck of cards.

Question 13

The relative frequency approach to probability is judgmental,representing the degree to which one happens to believe that an event will or will not happen.

Question 14

When events A and B are independent,then P(A and B)= P(A)+ P(B).

Question 15

In the classical approach,probability is the proportion of times an event is observed to occur in a very larger number of trials.

Question 16

In general,an event is one of the possible outcomes of an experiment.

Question 17

The union of events describes two or more events occurring at the same time.

Question 18

If a set of events includes all the possible outcomes of an experiment,these events are considered to be:

A) mutually exclusive.
B) exhaustive.
C) intersecting.
D) inclusive.
E) None of the above.

Question 19

If P(A)= 0.5 and P(B)= 0.80,then P(A or B)must be 0.95.

Question 20

A student is randomly selected from a class.Event A = the student is a male and Event B = the student is a female.Events A and B are:

A) mutually exclusive.
B) exhaustive.
C) intersecting.
D) dependent.
E) both A and B.

Question 21

The table below gives the probabilities of combinations of religion and political parties in a major U.S.city. $$\begin{array}{l}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \text { Religion }\\\begin{array} { | l | c c c c | } \hline\text { Political parties } & \text { Protestant } ( A ) & \text { Catholic } ( B ) & \text { Jewish } ( C ) & \text { Other } ( D ) \\\hline \text { Democrat } ( E ) & 0.35 & 0.10 & 0.03 & 0.02 \\\text { Republican } ( F ) & 0.27 & 0.09 & 0.02 & 0.01 \\\text { Independent } ( G ) & 0.05 & 0.03 & 0.02 & 0.01 \\\hline\end{array}\end{array}$$

-Which two of the following pairs of events intersect?

A) A and D
B) A and E
C) F and E
D) B and C
E) D and B

Question 22

If a contingency table shows the sex and classification of undergraduate students (freshman,sophomore,junior,senior)in your statistics class,which of the following is true?

A) The sex of the student is an example of mutually exclusive events.
B) Because yours is an undergraduate class,the events are exhaustive,i.e.,each student must fall in one of the classifications.
C) An example for the intersection of events would be the number of males who are juniors.
D) An example for the union of events would be the number of students who are female or juniors.
E) All of these are true.

Question 23

Which of the following statements is not correct?

A) Two events A and B are mutually exclusive if event A occurs and event B cannot occur.
B) If events A and B occur at the same time,then A and B intersect.
C) If event A does not occur,then its complement A' will also not occur.
D) A union of events occurs when at least one event in a group occurs,
E) If all possible outcomes of an experiment are represented in a set,the set is considered exhaustive.

Question 24

The table below gives the probabilities of combinations of religion and political parties in a major U.S.city. $$\begin{array}{l}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \text { Religion }\\\begin{array} { | l | c c c c | } \hline\text { Political parties } & \text { Protestant } ( A ) & \text { Catholic } ( B ) & \text { Jewish } ( C ) & \text { Other } ( D ) \\\hline \text { Democrat } ( E ) & 0.35 & 0.10 & 0.03 & 0.02 \\\text { Republican } ( F ) & 0.27 & 0.09 & 0.02 & 0.01 \\\text { Independent } ( G ) & 0.05 & 0.03 & 0.02 & 0.01 \\\hline\end{array}\end{array}$$

-What is the probability that a randomly selected person would be a Republican?

A) 0.67
B) 0.22
C) 0.11
D) 0.39
E) None of these

Question 25

Two events A and B are said to be mutually exclusive if:

A) P (A /B)= 1.
B) P (B /A)=1.
C) P (A and B)=1.
D) P (A and B)= 0.

Question 26

A useful graphical method of constructing the sample space for an experiment is:

A) tree diagram.
B) pie chart.
C) histogram.
D) bar graph.
E) scatter plot

Question 27

NARRBEGIN: Basketball Team
A basketball team at a university is composed of ten players.The team is made up of players who play either guard,forward,or center position.Four of the ten are guards; four of the ten are forwards; and two of the ten are centers.The numbers of the players are 1,2,3,4,for the guards; 5,6,7,8 for the forwards; and 9 and 10 for the centers.The starting five are numbered 1,3,5,7,and 9.Let a player be selected at random from the ten.Define the following events:
A = player selected has a number from 1 to 8.
B = player selected is a guard.
C = player selected is a forward.
D = player selected is a starter.
E = player selected is a center.
P(B /D)is equal to:

A) 0.80.
B) 0.40.
C) 0.50.
D) 0.20.
E) 0.60.

Question 28

NARRBEGIN: Basketball Team
A basketball team at a university is composed of ten players.The team is made up of players who play either guard,forward,or center position.Four of the ten are guards; four of the ten are forwards; and two of the ten are centers.The numbers of the players are 1,2,3,4,for the guards; 5,6,7,8 for the forwards; and 9 and 10 for the centers.The starting five are numbered 1,3,5,7,and 9.Let a player be selected at random from the ten.Define the following events:
A = player selected has a number from 1 to 8.
B = player selected is a guard.
C = player selected is a forward.
D = player selected is a starter.
E = player selected is a center.
P(E /D)is equal to:

A) 0.80.
B) 0.40.
C) 0.50.
D) 0.20.
E) 0.10.

Question 29

If P(A)= 0.25 and P(B)= 0.60,then P(A and B)is:

A) 0.15.
B) 0.35.
C) 0.85.
D) Cannot be determined from the information given.

Question 30

The table below gives the probabilities of combinations of religion and political parties in a major U.S.city. $$\begin{array}{l}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \text { Religion }\\\begin{array} { | l | c c c c | } \hline\text { Political parties } & \text { Protestant } ( A ) & \text { Catholic } ( B ) & \text { Jewish } ( C ) & \text { Other } ( D ) \\\hline \text { Democrat } ( E ) & 0.35 & 0.10 & 0.03 & 0.02 \\\text { Republican } ( F ) & 0.27 & 0.09 & 0.02 & 0.01 \\\text { Independent } ( G ) & 0.05 & 0.03 & 0.02 & 0.01 \\\hline\end{array}\end{array}$$

-What is the probability that a randomly selected person would be an independent whose religion was neither Protestant nor Catholic?

A) 0.05
B) 0.03
C) 0.02
D) 0.01

Question 31

NARRBEGIN: Basketball Team
A basketball team at a university is composed of ten players.The team is made up of players who play either guard,forward,or center position.Four of the ten are guards; four of the ten are forwards; and two of the ten are centers.The numbers of the players are 1,2,3,4,for the guards; 5,6,7,8 for the forwards; and 9 and 10 for the centers.The starting five are numbered 1,3,5,7,and 9.Let a player be selected at random from the ten.Define the following events:
A = player selected has a number from 1 to 8.
B = player selected is a guard.
C = player selected is a forward.
D = player selected is a starter.
E = player selected is a center.
P(A)is equal to:

A) 0.80.
B) 0.40.
C) 0.50.
D) 0.20.
E) 0.60.

Question 32

NARRBEGIN: Basketball Team
A basketball team at a university is composed of ten players.The team is made up of players who play either guard,forward,or center position.Four of the ten are guards; four of the ten are forwards; and two of the ten are centers.The numbers of the players are 1,2,3,4,for the guards; 5,6,7,8 for the forwards; and 9 and 10 for the centers.The starting five are numbered 1,3,5,7,and 9.Let a player be selected at random from the ten.Define the following events:
A = player selected has a number from 1 to 8.
B = player selected is a guard.
C = player selected is a forward.
D = player selected is a starter.
E = player selected is a center.
P(D and E)is equal to:

A) 0.10.
B) 0.05.
C) 0.50.
D) 0.20.
E) 0.60.

Question 33

The table below gives the probabilities of combinations of religion and political parties in a major U.S.city. $$\begin{array}{l}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \text { Religion }\\\begin{array} { | l | c c c c | } \hline\text { Political parties } & \text { Protestant } ( A ) & \text { Catholic } ( B ) & \text { Jewish } ( C ) & \text { Other } ( D ) \\\hline \text { Democrat } ( E ) & 0.35 & 0.10 & 0.03 & 0.02 \\\text { Republican } ( F ) & 0.27 & 0.09 & 0.02 & 0.01 \\\text { Independent } ( G ) & 0.05 & 0.03 & 0.02 & 0.01 \\\hline\end{array}\end{array}$$

-Which of the following represents two mutually exclusive events?

A) (A and D).
B) (A and E).
C) (A and F).
D) (A and G).
E) All of these are mutually exclusive.

Question 34

The table below gives the probabilities of combinations of religion and political parties in a major U.S.city. $$\begin{array}{l}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \text { Religion }\\\begin{array} { | l | c c c c | } \hline\text { Political parties } & \text { Protestant } ( A ) & \text { Catholic } ( B ) & \text { Jewish } ( C ) & \text { Other } ( D ) \\\hline \text { Democrat } ( E ) & 0.35 & 0.10 & 0.03 & 0.02 \\\text { Republican } ( F ) & 0.27 & 0.09 & 0.02 & 0.01 \\\text { Independent } ( G ) & 0.05 & 0.03 & 0.02 & 0.01 \\\hline\end{array}\end{array}$$

-What is the probability that a randomly selected person would be a Democrat who was not Jewish?

A) 0.93
B) 0.50
C) 0.47
D) 0.07
E) None of these

Question 35

If Events A and B are not mutually exclusive,then the probability that one of the events will occur is represented by

A) P(A or B)= P(A)+ P(B)- P(A and B)
B) P(A or B)= P(A)+ P(B)
C) P(A and B)= P(A)+ P(B)- P(A or B)
D) P(A and B)= P(A)+ P(B)
E) P(A or B)= P(A)+ P(B)+ P(A and B)

Question 36

If P(A)= 0.84,P(B)= 0.76 and P(A or B)= 0.90,then P(A and B)is:

A) 0.06.
B) 0.14.
C) 0.70.
D) 0.83.

Question 37

The table below gives the probabilities of combinations of religion and political parties in a major U.S.city. $$\begin{array}{l}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \text { Religion }\\\begin{array} { | l | c c c c | } \hline\text { Political parties } & \text { Protestant } ( A ) & \text { Catholic } ( B ) & \text { Jewish } ( C ) & \text { Other } ( D ) \\\hline \text { Democrat } ( E ) & 0.35 & 0.10 & 0.03 & 0.02 \\\text { Republican } ( F ) & 0.27 & 0.09 & 0.02 & 0.01 \\\text { Independent } ( G ) & 0.05 & 0.03 & 0.02 & 0.01 \\\hline\end{array}\end{array}$$

-What is the probability that a randomly selected person would be a Protestant and at the same time be a Democrat or a Republican?

A) 0.67
B) 0.35
C) 0.95
D) 0.89
E) 0.62

Question 38

Assume that A and B are independent events with P(A)= 0.40 and P(B)= 0.30.The probability that both events will occur simultaneously is:

A) 0.10.
B) 0.12.
C) 0.70.
D) 0.75.
E) 1.0.

Question 39

NARRBEGIN: Basketball Team
A basketball team at a university is composed of ten players.The team is made up of players who play either guard,forward,or center position.Four of the ten are guards; four of the ten are forwards; and two of the ten are centers.The numbers of the players are 1,2,3,4,for the guards; 5,6,7,8 for the forwards; and 9 and 10 for the centers.The starting five are numbered 1,3,5,7,and 9.Let a player be selected at random from the ten.Define the following events:
A = player selected has a number from 1 to 8.
B = player selected is a guard.
C = player selected is a forward.
D = player selected is a starter.
E = player selected is a center.
P(B and D)is equal to:

A) 0.80.
B) 0.40.
C) 0.50.
D) 0.20.
E) 0.30.

Question 40

NARRBEGIN: Basketball Team
A basketball team at a university is composed of ten players.The team is made up of players who play either guard,forward,or center position.Four of the ten are guards; four of the ten are forwards; and two of the ten are centers.The numbers of the players are 1,2,3,4,for the guards; 5,6,7,8 for the forwards; and 9 and 10 for the centers.The starting five are numbered 1,3,5,7,and 9.Let a player be selected at random from the ten.Define the following events:
A = player selected has a number from 1 to 8.
B = player selected is a guard.
C = player selected is a forward.
D = player selected is a starter.
E = player selected is a center.
P(B)is equal to:

A) 0.80.
B) 0.40.
C) 0.50.
D) 0.20.
E) 0.30.

Question 41

NARRBEGIN: Appliance dealer
An appliance dealer calculated the proportion of new dishwashers sold that required various numbers of service calls to correct problems during the warranty period.The records were: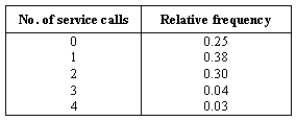
Let X be the number of service calls during the warranty period for a dishwasher.What is the probability that there will be at least one service call?

Question 42

NARRBEGIN: Overtime hours
A personnel manager is reviewing number of overtime hours worked by employees in her plant.She has compiled the following data: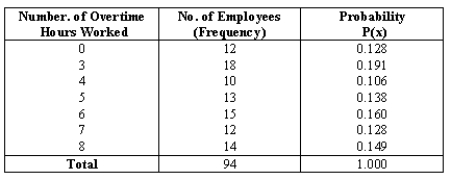 For a randomly selected employee let X be the number of overtime hours worked,and define the following events:
A = employee who works no overtime.
B = employee who works at least 7 hours overtime.
C = employee who works at most 4 hours overtime.
Determine the probability of event C.

Question 43

NARRBEGIN: College
The table below indicates the number of majors found in a college of business: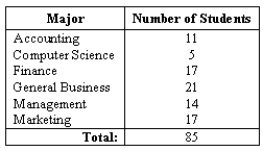
What is the probability that a randomly selected student is either a computer science major or a marketing major?

Question 44

Which of the following statements is correct given that the events A and B have nonzero probabilities?

A) A and B cannot be both independent and mutually exclusive
B) A and B can be both independent and mutually exclusive
C) A and B are always independent
D) A and B are always mutually exclusive

Question 45

NARRBEGIN: College
The table below indicates the number of majors found in a college of business:
What is the probability that a randomly selected student is a finance major and an accounting major?

Question 46

NARRBEGIN: Appliance dealer
An appliance dealer calculated the proportion of new dishwashers sold that required various numbers of service calls to correct problems during the warranty period.The records were:
Let X be the number of service calls during the warranty period for a dishwasher.What is the probability that there will be at most one service call?

Question 47

If A and B are independent events with P(A)= 0.25 and P(B)= 0.60,then P(A/B)is:

A) 0.25.
B) 0.60.
C) 0.35.
D) 0.85.
E) 0.15

Question 48

NARRBEGIN: Appliance dealer
An appliance dealer calculated the proportion of new dishwashers sold that required various numbers of service calls to correct problems during the warranty period.The records were:
Let X be the number of service calls during the warranty period for a dishwasher.What is the probability that there will be at least one service call but not more than 3?

Question 49

NARRBEGIN: Appliance dealer
An appliance dealer calculated the proportion of new dishwashers sold that required various numbers of service calls to correct problems during the warranty period.The records were:
Let X be the number of service calls during the warranty period for a dishwasher.What is the probability that there will be exactly one service call?

Question 50

A survey revealed that 21.5% of the households had no checking account,66.9% had regular checking accounts,and 11.6% had NOW accounts.Of those households with no checking account 40% had savings accounts.Of the households with regular checking accounts 71.6% had a savings account.Of the households with NOW accounts 79.3% had savings accounts. The probability that a randomly selected household has no checking account and no savings account is:

A) 0.0860.
B) 0.1290.
C) 0.5330.
D) 0.1309.
E) 0.3430.

Question 51

NARRBEGIN: Overtime hours
A personnel manager is reviewing number of overtime hours worked by employees in her plant.She has compiled the following data: For a randomly selected employee let X be the number of overtime hours worked,and define the following events:
A = employee who works no overtime.
B = employee who works at least 7 hours overtime.
C = employee who works at most 4 hours overtime.
Determine the probability of event B.

Question 52

A survey revealed that 21.5% of the households had no checking account,66.9% had regular checking accounts,and 11.6% had NOW accounts.Of those households with no checking account 40% had savings accounts.Of the households with regular checking accounts 71.6% had a savings account.Of the households with NOW accounts 79.3% had savings accounts. The probability that a randomly selected household with a savings account has no checking account is:

A) 0.1309.
B) 0.1290.
C) 0.1437.
D) 0.2150.
E) 0.4000.

Question 53

NARRBEGIN: Appliance dealer
An appliance dealer calculated the proportion of new dishwashers sold that required various numbers of service calls to correct problems during the warranty period.The records were:
Let X be the number of service calls during the warranty period for a dishwasher.What is the probability that there will be between two and four (inclusive)service calls?

Question 54

A survey revealed that 21.5% of the households had no checking account,66.9% had regular checking accounts,and 11.6% had NOW accounts.Of those households with no checking account 40% had savings accounts.Of the households with regular checking accounts 71.6% had a savings account.Of the households with NOW accounts 79.3% had savings accounts. The probability that a randomly selected household has a savings account is:

A) 0.609.
B) 1.000.
C) 0.227.
D) 0.657.
E) 0.537.

Question 55

Two events A and B are said to be independent if:

A) P(A and B)= P(A)· P(B).
B) P(A and B)= P(A)+ P(B).
C) P(A/B)= P(B).
D) P(B/A)= P(A).
E) P(A or B)= P(A)· P(B).

Question 56

The odds of the Dallas Cowboys winning this year's Super Bowl are 3 to 1.Compute the probability of the Cowboys winning.

Question 57

NARRBEGIN: Overtime hours
A personnel manager is reviewing number of overtime hours worked by employees in her plant.She has compiled the following data: For a randomly selected employee let X be the number of overtime hours worked,and define the following events:
A = employee who works no overtime.
B = employee who works at least 7 hours overtime.
C = employee who works at most 4 hours overtime.
Determine the probability of event A.

Question 58

The joint probability of Events A and B is described as:

A) The probability of Event A,given that Event B has occurred.
B) The probability of Event B,given that Event A has occurred.
C) The probability that either Event A or Event B has occurred.
D) The probability that both Event A and Event B has occurred.

Question 59

If the probability of drawing an Ace from a deck of cards is 0.077 and the probability of rolling a "2" using a fair die is 0.167,then the probability of drawing an Ace and rolling a "2" is

A) 0.244
B) 0.090
C) 0.454
D) 0.013
E) 0.333

Question 60

NARRBEGIN: College
The table below indicates the number of majors found in a college of business:
What is the probability that a randomly selected student is an accounting major?

Question 61

NARRBEGIN: Telephone survey
A political telephone survey of 360 people asked whether they were in favor or not in favor of a proposed law.Each person was identified as either Republican or Democrat.The results are shown in the following table:

What is the probability that a randomly selected respondent was a Democrat?

Question 62

NARRBEGIN: Telephone survey
A political telephone survey of 360 people asked whether they were in favor or not in favor of a proposed law.Each person was identified as either Republican or Democrat.The results are shown in the following table:

What is the probability that a randomly selected respondent was a Democrat or not in favor of the proposed law?

Question 63

NARRBEGIN: Event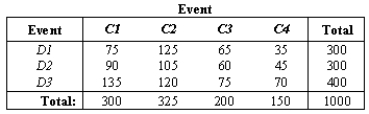
Find P (D1)or P (C1).

Question 64

NARRBEGIN: Candidate
Six candidates for a new position of vice-president for academic affairs have been selected.Three of the candidates are female.The candidates' years of experience are as follows: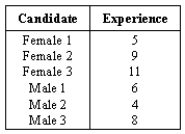 Suppose one of the candidates is selected at random.Define the following events:
A = person selected has 9 years experience.
B = person selected is a female.
Find P(A).

Question 65

NARRBEGIN: Manufacturers
A large men's store in a mall purchases suits from four different manufacturers in short,regular,and long.Their current selections are given in the contingency table below: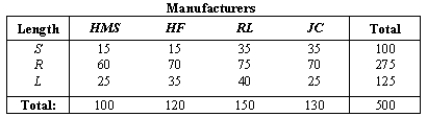 Let the abbreviations and letters represent the events.For example Event S = a randomly selected suit is short,event HMS = a randomly selected suit is manufactured by HMS.
Compute P(S).

Question 66

NARRBEGIN: Odds
The odds in favor of an event are the number of successes divided by the number of failures.The probability of this event occurring is the number of successes divided by the sum of the number of successes and the number of failures.The number of successes is five and the number of failures is four.
Find the probability of failure.

Question 67

NARRBEGIN: Event
Find P (D1 or D2 or D3).

Question 68

NARRBEGIN: Manufacturers
A large men's store in a mall purchases suits from four different manufacturers in short,regular,and long.Their current selections are given in the contingency table below: Let the abbreviations and letters represent the events.For example Event S = a randomly selected suit is short,event HMS = a randomly selected suit is manufactured by HMS.
Compute P(HMS / S).

Question 69

NARRBEGIN: Candidate
Six candidates for a new position of vice-president for academic affairs have been selected.Three of the candidates are female.The candidates' years of experience are as follows: Suppose one of the candidates is selected at random.Define the following events:
A = person selected has 9 years experience.
B = person selected is a female.
Find P(B).

Question 70

NARRBEGIN: Event
Find P (C1 and D1).

Question 71

NARRBEGIN: Manufacturers
A large men's store in a mall purchases suits from four different manufacturers in short,regular,and long.Their current selections are given in the contingency table below: Let the abbreviations and letters represent the events.For example Event S = a randomly selected suit is short,event HMS = a randomly selected suit is manufactured by HMS.
Compute P(HMS).

Question 72

NARRBEGIN: Telephone survey
A political telephone survey of 360 people asked whether they were in favor or not in favor of a proposed law.Each person was identified as either Republican or Democrat.The results are shown in the following table:

What is the probability that a randomly selected respondent was a Republican and undecided about the proposed law?

Question 73

In the board game called TRIVIAL PURSUIT,a single die is used to determine the number of spaces a player is allowed to move.A player is currently positioned 3 spaces from a space where a correct answer will earn a "pie" and 4 spaces from a space where "roll again" is the option.Assuming a fair die,what is the probability the player will get to answer a question for a "pie" or get to "roll again"?

Question 74

NARRBEGIN: Candidate
Six candidates for a new position of vice-president for academic affairs have been selected.Three of the candidates are female.The candidates' years of experience are as follows: Suppose one of the candidates is selected at random.Define the following events:
A = person selected has 9 years experience.
B = person selected is a female.
Find P(not A / B).

Question 75

NARRBEGIN: Candidate
Six candidates for a new position of vice-president for academic affairs have been selected.Three of the candidates are female.The candidates' years of experience are as follows: Suppose one of the candidates is selected at random.Define the following events:
A = person selected has 9 years experience.
B = person selected is a female.
Find P(A / B).

Question 76

NARRBEGIN: Manufacturers
A large men's store in a mall purchases suits from four different manufacturers in short,regular,and long.Their current selections are given in the contingency table below: Let the abbreviations and letters represent the events.For example Event S = a randomly selected suit is short,event HMS = a randomly selected suit is manufactured by HMS.
Compute P(S /HMS).

Question 77

NARRBEGIN: Manufacturers
A large men's store in a mall purchases suits from four different manufacturers in short,regular,and long.Their current selections are given in the contingency table below: Let the abbreviations and letters represent the events.For example Event S = a randomly selected suit is short,event HMS = a randomly selected suit is manufactured by HMS.
Compute P(S and HMS).

Question 78

NARRBEGIN: Event
Find P (C1 or D1).

Question 79

NARRBEGIN: Shoe store
A shoe store carries 590 pairs of Stacy-Adams and 610 pairs of Freeman brands of shoes.Let a success be the event of randomly selecting a pair of Stacy-Adams shoes.
Find the probability of a success.

Question 80

NARRBEGIN: Telephone survey
A political telephone survey of 360 people asked whether they were in favor or not in favor of a proposed law.Each person was identified as either Republican or Democrat.The results are shown in the following table:

What is the probability that a randomly selected respondent was in favor of the proposed law?