Deck 10: Differential Equations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/126
Play
Full screen (f)
Deck 10: Differential Equations
1
Consider the differential equation y' = y - 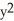 . Which of the following statements is/are true?
. Which of the following statements is/are true?
A) The function f(t) =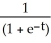 is a solution to this differential equation with initial condition
is a solution to this differential equation with initial condition 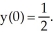
B) This differential equation has infinitely many solutions.
C) The constant function f(t) = 1 is a solution to this differential equation.
D) If f(t) is a solution to the differential equation satisfying the initial condition y(0) = 0, then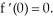
E) All of these statements are true.
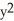 . Which of the following statements is/are true?
. Which of the following statements is/are true?A) The function f(t) =
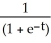 is a solution to this differential equation with initial condition
is a solution to this differential equation with initial condition 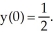
B) This differential equation has infinitely many solutions.
C) The constant function f(t) = 1 is a solution to this differential equation.
D) If f(t) is a solution to the differential equation satisfying the initial condition y(0) = 0, then
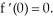
E) All of these statements are true.
All of these statements are true.
2
Consider the differential equation 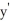 =
=  (y + 3). Which of the following statements is/are true?
(y + 3). Which of the following statements is/are true?
(I) f(t) = -3 is a constant solution to this differential equation.
(II) f(t) = 0 is a constant solution to this differential equation.
(III) If f(t) is a solution to the differential equation with initial conditions y(1) = 0, then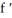 (1) = 3.
(1) = 3.
A) I and III
B) II only
C) III only
D) I only
E) I, II, and III
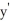 =
= 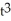 (y + 3). Which of the following statements is/are true?
(y + 3). Which of the following statements is/are true?(I) f(t) = -3 is a constant solution to this differential equation.
(II) f(t) = 0 is a constant solution to this differential equation.
(III) If f(t) is a solution to the differential equation with initial conditions y(1) = 0, then
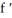 (1) = 3.
(1) = 3.A) I and III
B) II only
C) III only
D) I only
E) I, II, and III
I and III
3
Solve the differential equation: y' = 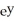 sin t.
sin t.
A) y = cos(ln t) + C
B) y =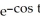 + C
+ C
C) y = ln(-sin t) + C
D) y = -ln(cos t + C
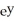 sin t.
sin t.A) y = cos(ln t) + C
B) y =
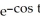 + C
+ CC) y = ln(-sin t) + C
D) y = -ln(cos t + C
y = -ln(cos t + C
4
Given the differential equation: 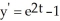 , is this the solution
, is this the solution 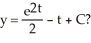
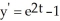 , is this the solution
, is this the solution 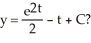

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
5
Which of the following functions solves the differential equation: 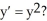
A) y = -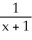
B) y = -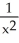
C) y = ln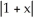
D) y =
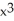
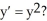
A) y = -
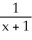
B) y = -
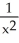
C) y = ln
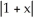
D) y =

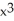

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
6
Find f'(1) if f(t) is a solution to the initial value problem: 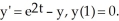 Enter just a real number (no approximations).
Enter just a real number (no approximations).
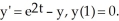 Enter just a real number (no approximations).
Enter just a real number (no approximations).
Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
7
Which of the following functions solves the differential equation: 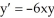 ?
?
A) y =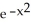
B) y =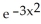
C) y = 7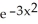
D) y = 7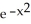
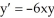 ?
?A) y =
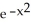
B) y =
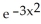
C) y = 7
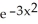
D) y = 7
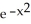

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
8
Find a constant solution of 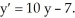 Enter just a reduced fraction of form
Enter just a reduced fraction of form 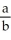 .
.
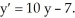 Enter just a reduced fraction of form
Enter just a reduced fraction of form 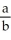 .
.
Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
9
Given the differential equation: 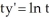 , is this the solution
, is this the solution 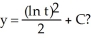
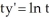 , is this the solution
, is this the solution 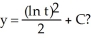

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
10
Given the differential equation: 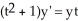 , is this the solution
, is this the solution 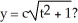
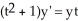 , is this the solution
, is this the solution 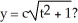

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
11
Find f'(1) if f(t) is a solution to the initial value problem: 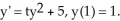 Enter just an integer.
Enter just an integer.
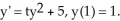 Enter just an integer.
Enter just an integer.
Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
12
Which of the following functions solves the differential equation: 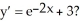
A) y =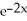 + 3
+ 3
B) y =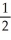
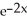 + 3
+ 3
C) y = -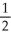
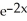 + 3x
+ 3x
D) none of these
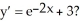
A) y =
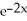 + 3
+ 3B) y =
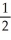
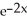 + 3
+ 3C) y = -
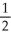
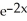 + 3x
+ 3xD) none of these

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
13
Given the differential equation: y' is this the solution 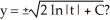
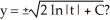

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
14
Find f'(0) if f(t) is a solution to the initial value problem: 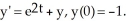 Enter just an integer.
Enter just an integer.
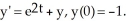 Enter just an integer.
Enter just an integer.
Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
15
Given the differential equation: 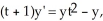 is this the solution
is this the solution 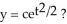
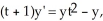 is this the solution
is this the solution 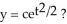

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
16
Given the differential equation: 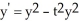 , is this the solution:
, is this the solution: 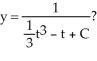
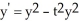 , is this the solution:
, is this the solution: 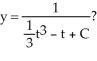

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
17
Find a constant solution of 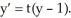 Enter just an integer.
Enter just an integer.
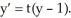 Enter just an integer.
Enter just an integer.
Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
18
Given the differential equation: 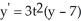 , is this the solution
, is this the solution 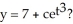
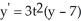 , is this the solution
, is this the solution 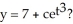

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
19
Which of the following functions solves the differential equation: 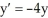 ?
?
A) y =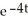
B) y = -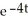
C) y = ln 4t
D) none of these
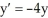 ?
?A) y =
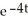
B) y = -
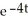
C) y = ln 4t
D) none of these

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
20
Write a differential equation that expresses the following description of a rate: When ice cream is removed from the freezer, it warms up at a rate proportional to the difference between the temperature of the ice cream and the room temperature of 76°. (Use y for the temperature of the ice cream, t for the time, and k for an unknown constant.)
A) y' = 76 - ky
B) y' = k(76 - y)
C) y' = k(76 - t)
D) y' = 76t - ky
A) y' = 76 - ky
B) y' = k(76 - y)
C) y' = k(76 - t)
D) y' = 76t - ky

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
21
Solve the differential equation with the given initial condition.
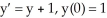
A) y =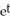 - 2
- 2
B) y = 2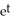 -1
-1
C) y =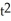 + 1
+ 1
D) y = t + 1
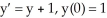
A) y =
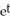 - 2
- 2B) y = 2
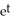 -1
-1C) y =
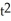 + 1
+ 1D) y = t + 1

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
22
Solve the differential equation with the given initial condition.
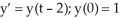
A) y =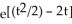 - 2t + 1
- 2t + 1
B) y =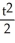 - 2t
- 2t
C) y =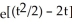
D) y = 0
E) none of these
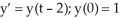
A) y =
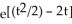 - 2t + 1
- 2t + 1B) y =
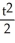 - 2t
- 2tC) y =
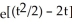
D) y = 0
E) none of these

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
23
Given the differential equation with the given initial condition: 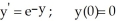 is this the solution
is this the solution 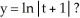
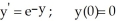 is this the solution
is this the solution 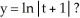

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
24
Solve the differential equation with the given initial condition.
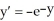 , y(0) = 0
, y(0) = 0
A) y = -ln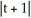
B) y = 0
C) y =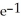
D) y =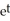
E) none of these
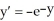 , y(0) = 0
, y(0) = 0A) y = -ln
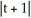
B) y = 0
C) y =
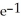
D) y =
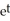
E) none of these

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
25
Given the differential equation with the given initial condition: 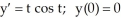 is this the solution
is this the solution 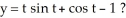
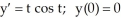 is this the solution
is this the solution 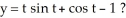

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
26
Given the differential equation with the given initial condition: 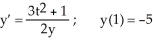 is this the solution
is this the solution 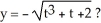
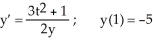 is this the solution
is this the solution 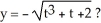

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
27
Solve the differential equation with the given initial condition.
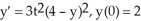
A) y = 4 -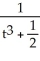
B) y =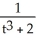
C) y =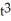 +
+ 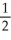
D) y = 4 +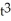
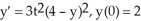
A) y = 4 -
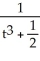
B) y =
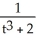
C) y =
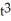 +
+ 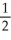
D) y = 4 +
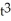

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
28
Let t represent the number of hours that a packing machine is operated and y(t) represent the probability that the machine breaks down at least once during the t hours of operation. It has been observed that the rate of increase of the probability of a breakdown is proportional to the probability of not having a breakdown. Find a differential equation describing this situation.
A)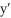 = ky; There is not enough information given to determine initial conditions.
= ky; There is not enough information given to determine initial conditions.
B)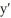 = ky; y(0) = 0
= ky; y(0) = 0
C)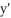 = k(1 - y); There is not enough information given to determine initial conditions.
= k(1 - y); There is not enough information given to determine initial conditions.
D)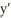 = k(1 - y); y(0) = 0
= k(1 - y); y(0) = 0
E)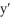 = (1 + y); y(0) =0
= (1 + y); y(0) =0
A)
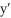 = ky; There is not enough information given to determine initial conditions.
= ky; There is not enough information given to determine initial conditions.B)
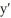 = ky; y(0) = 0
= ky; y(0) = 0C)
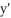 = k(1 - y); There is not enough information given to determine initial conditions.
= k(1 - y); There is not enough information given to determine initial conditions.D)
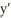 = k(1 - y); y(0) = 0
= k(1 - y); y(0) = 0E)
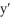 = (1 + y); y(0) =0
= (1 + y); y(0) =0
Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
29
Given the differential equation with the given initial condition: 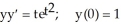 is this the solution
is this the solution 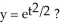
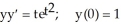 is this the solution
is this the solution 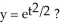

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
30
Solve the differential equation with the given initial condition.
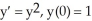
A) t + 1
B)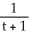
C) t - 1
D)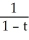
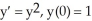
A) t + 1
B)
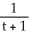
C) t - 1
D)
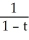

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
31
Find the constant solutions to the differential equation: 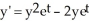 .
.
Enter just one integer or two separated by a comma (no label).
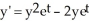 .
.Enter just one integer or two separated by a comma (no label).

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
32
Solve the differential equation with the given initial condition.
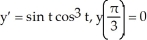
A) y =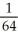 -
- 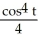
B) y =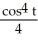
C) y = 16 +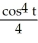
D) y = 64 -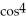 t
t
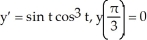
A) y =
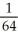 -
- 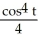
B) y =
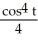
C) y = 16 +
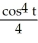
D) y = 64 -
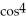 t
t
Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
33
Given the differential equation with the given initial condition: 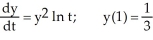 is this the solution
is this the solution 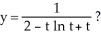
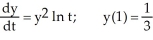 is this the solution
is this the solution 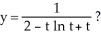

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
34
Given the differential equation with the given initial condition: 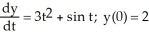 is this the solution
is this the solution 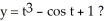
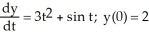 is this the solution
is this the solution 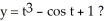

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
35
Solve the differential equation with the given initial condition.
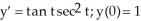
A) y = ln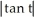 + 1
+ 1
B) y =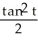 + 1
+ 1
C) y = tan t + 1
D) y =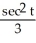 +
+ 
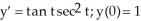
A) y = ln
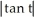 + 1
+ 1B) y =
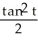 + 1
+ 1C) y = tan t + 1
D) y =
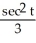 +
+ 

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
36
Solve the differential equation with the given initial condition.
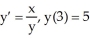
A) y =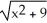
B) y = ±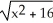
C) y = ±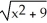
D) y =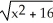
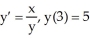
A) y =
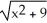
B) y = ±
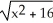
C) y = ±
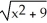
D) y =
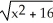

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
37
Given the differential equation: 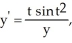 is this the solution
is this the solution 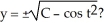
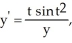 is this the solution
is this the solution 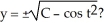

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
38
Given the differential equation with the given initial condition: 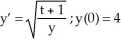 is this the solution
is this the solution 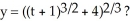
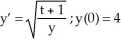 is this the solution
is this the solution 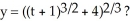

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
39
Solve the differential equation with the given initial condition.
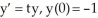
A) y =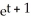
B) y = -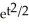
C) y =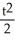
D) y = -1 +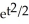
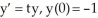
A) y =
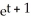
B) y = -
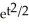
C) y =
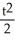
D) y = -1 +
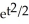

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
40
Given the differential equation: 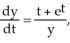 is this the solution
is this the solution 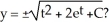
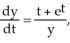 is this the solution
is this the solution 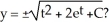

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
41
Find the integrating factor, the general solution, and the particular solution satisfying the initial condition. 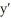 - 4y = -2
- 4y = -2 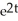 ; y(0) = -1
; y(0) = -1
A) integrating factor: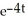
General solution: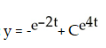
Particular solution: y = -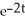 - 2
- 2 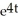
B) integrating factor: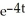
General solution: y =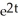 + C
+ C 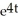
Particular solution: y =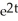 - 2
- 2 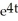
C) integrating factor: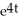
General solution: y = -2t + C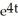
Particular solution: y = -2t -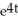
D) integrating factor: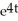
General solution: y =
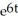 + C
+ C 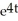
Particular solution: y =
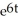 -
- 
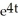
Solve the equation using an integrating factor.
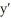 - 4y = -2
- 4y = -2 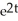 ; y(0) = -1
; y(0) = -1A) integrating factor:
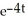
General solution:
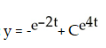
Particular solution: y = -
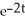 - 2
- 2 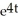
B) integrating factor:
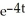
General solution: y =
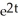 + C
+ C 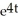
Particular solution: y =
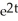 - 2
- 2 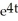
C) integrating factor:
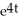
General solution: y = -2t + C
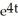
Particular solution: y = -2t -
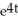
D) integrating factor:
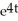
General solution: y =

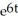 + C
+ C 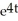
Particular solution: y =

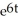 -
- 
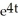
Solve the equation using an integrating factor.

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
42
Solve the initial value problem using an integrating factor.
t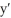 + 3y = 5t;
+ 3y = 5t; 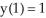 , t > 0
, t > 0
A) y = t -
t - 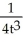
B) y =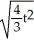 + 1 -
+ 1 - 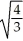
C) y = 5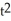 - 4t
- 4t
D) y = 5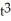 - 4
- 4 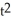
t
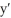 + 3y = 5t;
+ 3y = 5t; 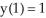 , t > 0
, t > 0A) y =
 t -
t - 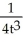
B) y =
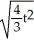 + 1 -
+ 1 - 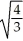
C) y = 5
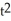 - 4t
- 4tD) y = 5
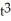 - 4
- 4 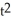

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
43
The annual sales y (in millions of dollars) of a company satisfy the differential equation 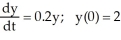 . Which of the following is a verbal description of the rate of change of annual sales ?
. Which of the following is a verbal description of the rate of change of annual sales ?
A) The annual sales are increasing at a rate proportional to the annual sales.
B) The annual sales are increasing at $0.2 million ($200,000) per year.
C) The annual sales are decreasing at a rate proportional to the annual sales.
D) The annual sales are increasing at a rate proportional to $0.2 million ($200,000) per year.
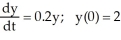 . Which of the following is a verbal description of the rate of change of annual sales ?
. Which of the following is a verbal description of the rate of change of annual sales ?A) The annual sales are increasing at a rate proportional to the annual sales.
B) The annual sales are increasing at $0.2 million ($200,000) per year.
C) The annual sales are decreasing at a rate proportional to the annual sales.
D) The annual sales are increasing at a rate proportional to $0.2 million ($200,000) per year.

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
44
Combine the terms y and 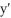 into the derivative of a product, then solve the equation.
into the derivative of a product, then solve the equation. 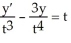 Is this the solution:
Is this the solution: 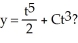
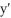 into the derivative of a product, then solve the equation.
into the derivative of a product, then solve the equation. 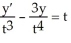 Is this the solution:
Is this the solution: 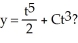

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
45
Solve the problem.
An initial deposit of $24,000 is made into an account that earns 5% compounded continuously. Money is then withdrawn at a constant rate of $4000 a year until the amount in the account is 0. Find the equation for the amount in the account at any time t. When is the amount 0?
A) A = 60,000 - 36,000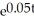 = 10)017 years
= 10)017 years
B) A = 80,000 - 56,000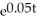 = 8)352 years
= 8)352 years
C) A = 80,000 - 56,000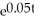 = 7)134 years
= 7)134 years
D) A = 60,000 - 36,000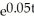 = 8)352 years
= 8)352 years
An initial deposit of $24,000 is made into an account that earns 5% compounded continuously. Money is then withdrawn at a constant rate of $4000 a year until the amount in the account is 0. Find the equation for the amount in the account at any time t. When is the amount 0?
A) A = 60,000 - 36,000
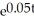 = 10)017 years
= 10)017 yearsB) A = 80,000 - 56,000
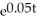 = 8)352 years
= 8)352 yearsC) A = 80,000 - 56,000
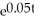 = 7)134 years
= 7)134 yearsD) A = 60,000 - 36,000
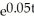 = 8)352 years
= 8)352 years
Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
46
Combine the terms y and 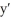 into the derivative of a product:
into the derivative of a product: 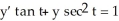 .
.
Is this derivative correct: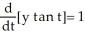 ?
?
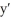 into the derivative of a product:
into the derivative of a product: 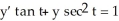 .
.Is this derivative correct:
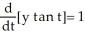 ?
?
Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
47
Solve the equation using an integrating factor.
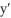 +
+ 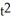 y = 4
y = 4 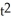 , t > 0
, t > 0
A) y = 4x + C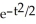
B) y = 4x + C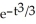
C) y = 4 + C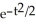
D) y = 4 + C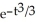
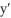 +
+ 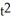 y = 4
y = 4 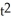 , t > 0
, t > 0A) y = 4x + C
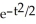
B) y = 4x + C
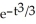
C) y = 4 + C
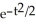
D) y = 4 + C
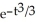

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
48
A cool object is to be heated to a maximum temperature M = M°C. At any time t, the rate at which the temperature rises is proportional to the difference between the actual temperature and the maximal temperature. If the object is originally 0°C, find and solve a differential equation describing this situation. Is this the solution: 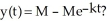
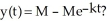

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
49
Solve the initial value problem using an integrating factor.
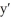 + y = 3; y(0) = 0.
+ y = 3; y(0) = 0.
A) y =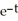 (3t -
(3t - 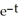 )
)
B) y =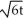
C) y = 3 - 3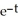
D) y = 3t
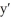 + y = 3; y(0) = 0.
+ y = 3; y(0) = 0.A) y =
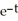 (3t -
(3t - 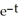 )
)B) y =
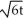
C) y = 3 - 3
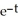
D) y = 3t

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
50
Suppose water is seeping from an underground storage facility at a rate that is proportional to the square amount of water present. If f(t) = y is the amount of water present at time t, find a differential equation describing the situation.
A)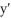 =
= 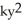 , k < 0
, k < 0
B)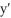 =
= 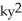 , k > 0
, k > 0
C)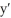 =
= 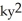 , k < 0; y(0) =0
, k < 0; y(0) =0
D)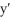 =
= 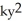 , k > 0; y(0) = 0
, k > 0; y(0) = 0
E) none of these
A)
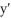 =
= 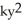 , k < 0
, k < 0B)
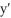 =
= 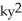 , k > 0
, k > 0C)
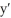 =
= 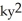 , k < 0; y(0) =0
, k < 0; y(0) =0D)
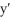 =
= 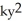 , k > 0; y(0) = 0
, k > 0; y(0) = 0E) none of these

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
51
Solve the equation using an integrating factor.
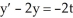 , t > 0
, t > 0
A) y = t + 1/2 + C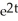
B) y = t - C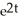
C) y = Ct +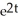
D) y = 1/2 + C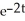
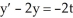 , t > 0
, t > 0A) y = t + 1/2 + C
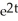
B) y = t - C
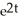
C) y = Ct +
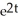
D) y = 1/2 + C
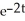

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
52
Combine the terms y and 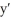 into the derivative of a product, then solve the equation.
into the derivative of a product, then solve the equation. 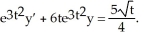 Is this the solution:
Is this the solution: 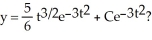
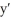 into the derivative of a product, then solve the equation.
into the derivative of a product, then solve the equation. 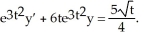 Is this the solution:
Is this the solution: 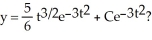

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
53
The annual sales y (in millions of dollars) of a company satisfy the differential equation 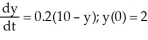 . Which of the following is a verbal description of the rate of change of annual sales.
. Which of the following is a verbal description of the rate of change of annual sales.
A) The annual sales are decreasing at a rate proportional to the annual sales.
B) The annual sales are increasing at $0.2 million ($200,000) per year to an upper limit of $5 million.
C) The annual sales are increasing at a rate proportional to the difference between the annual sales and an upper limit of $10 million.
D) The annual sales are increasing at a rate proportional to $0.2 million ($200,000) per year.
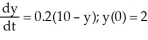 . Which of the following is a verbal description of the rate of change of annual sales.
. Which of the following is a verbal description of the rate of change of annual sales.A) The annual sales are decreasing at a rate proportional to the annual sales.
B) The annual sales are increasing at $0.2 million ($200,000) per year to an upper limit of $5 million.
C) The annual sales are increasing at a rate proportional to the difference between the annual sales and an upper limit of $10 million.
D) The annual sales are increasing at a rate proportional to $0.2 million ($200,000) per year.

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
54
Solve the equation using an integrating factor.
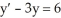 , t > 0
, t > 0
A) y = C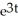 + C
+ C
B) y = C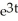
C) y = C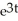 - 2
- 2
D) y = C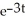
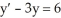 , t > 0
, t > 0A) y = C
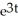 + C
+ CB) y = C
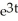
C) y = C
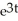 - 2
- 2D) y = C
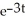

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
55
Suppose the relationship between the price p, of a product and the weekly sales, s, of the product is given by the differential equation 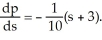 Then
Then
A) as sales increase, the price increases.
B) as the price increases the rate of change of the price also increases.
C) the rate of the decrease of the price is proportional to the sales.
D) s = 0 is a constant solution to this differential equation.
E) all of these
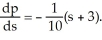 Then
ThenA) as sales increase, the price increases.
B) as the price increases the rate of change of the price also increases.
C) the rate of the decrease of the price is proportional to the sales.
D) s = 0 is a constant solution to this differential equation.
E) all of these

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
56
v
An initial deposit of $8,000 is made into an account earning 6.5% compounded continuously. Thereafter, money is deposited into the account at a constant rate of $2600 per year. Find the amount in this account at any time t. How much is in this account after 5 years?
A) A = 60,000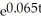 - 52,000= $31,041.84
- 52,000= $31,041.84
B) A = 52,000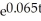 - 44,000= $27,969.59
- 44,000= $27,969.59
C) A = 48,000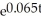 - 40,000= $26,433.47
- 40,000= $26,433.47
D) A = 44,000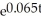 - 36,000= $24,897.34
- 36,000= $24,897.34
An initial deposit of $8,000 is made into an account earning 6.5% compounded continuously. Thereafter, money is deposited into the account at a constant rate of $2600 per year. Find the amount in this account at any time t. How much is in this account after 5 years?
A) A = 60,000
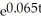 - 52,000= $31,041.84
- 52,000= $31,041.84B) A = 52,000
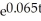 - 44,000= $27,969.59
- 44,000= $27,969.59C) A = 48,000
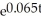 - 40,000= $26,433.47
- 40,000= $26,433.47D) A = 44,000
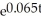 - 36,000= $24,897.34
- 36,000= $24,897.34
Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
57
Find the integrating factor, the general solution, and the particular solution satisfying the initial condition. 2t 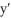 - y =
- y =  ; y(1) = -1, t > 0
; y(1) = -1, t > 0
A) integrating factor:\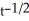
General solution: y = - + C
+ C 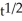
Particular solution: y = - +
+ 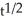
B) integrating factor: 2t
General solution: y = -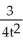 +
+ 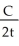
Particular solution: y = -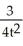 +
+ 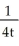
C) integrating factor: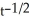
General solution: y = -4 + C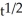
Particular solution: y = -4 + 3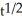
D) integrating factor: 2t
General solution: y = -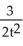 +
+ 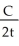
Particular solution: y = -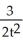 +
+ 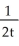
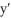 - y =
- y =  ; y(1) = -1, t > 0
; y(1) = -1, t > 0A) integrating factor:\
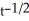
General solution: y = -
 + C
+ C 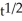
Particular solution: y = -
 +
+ 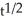
B) integrating factor: 2t
General solution: y = -
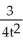 +
+ 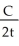
Particular solution: y = -
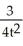 +
+ 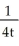
C) integrating factor:
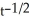
General solution: y = -4 + C
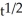
Particular solution: y = -4 + 3
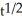
D) integrating factor: 2t
General solution: y = -
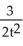 +
+ 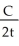
Particular solution: y = -
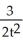 +
+ 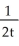

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
58
Solve the equation using an integrating factor.
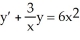 , t > 0
, t > 0
A) y =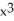 + C
+ C 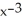
B) y = C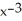
C) y =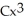 +
+ 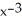
D) y =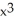 + C
+ C
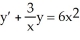 , t > 0
, t > 0A) y =
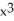 + C
+ C 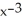
B) y = C
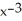
C) y =
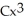 +
+ 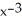
D) y =
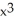 + C
+ C
Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
59
Solve the equation using an integrating factor.
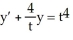 , t > 0
, t > 0
A) y = C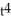 +
+ 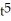
B) y = -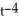 +
+ 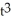 + C
+ C
C) y =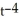 +
+ 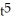
D) y = C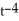 +
+ 
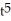
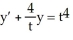 , t > 0
, t > 0A) y = C
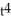 +
+ 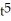
B) y = -
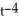 +
+ 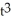 + C
+ CC) y =
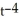 +
+ 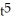
D) y = C
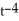 +
+ 

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
60
Combine the terms y and 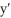 into the derivative of a product:
into the derivative of a product: 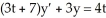 .
.
Is this derivative correct: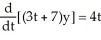 ?
?
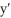 into the derivative of a product:
into the derivative of a product: 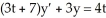 .
.Is this derivative correct:
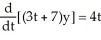 ?
?
Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
61
A jug of milk at 50° is placed outdoors at a temperature of 100°. If after 5 minutes the temperature of the milk is 60°, write the equation giving the temperature of the milk as a function of time. Enter your answer exactly as:
T = a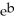 + c
+ c
T = a
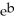 + c
+ c
Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
62
A tank contains 2000 L of a solution consisting of 50 kg of salt dissolved in water. Pure water is pumped into the tank at the rate of 10L/s, and the mixture (kept uniform by stirring) is pumped out at the same rate. How long will it be until only 5 kg of salt remain in the tank?
A) approximately 689 seconds
B) approximately 703 seconds
C) approximately 460 seconds
D) approximately 276 seconds
A) approximately 689 seconds
B) approximately 703 seconds
C) approximately 460 seconds
D) approximately 276 seconds

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
63
A fly population increases at a rate proportional to the amount present. After two years the population has doubled. After three years it is 20,000. Find the number of flies initially present. Enter just an integer.

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
64
How much would you need to invest per month - in effect, continuously - in an investment account that pays an annual interest rate of 9%, compounded continuously, in order for the account to be worth $100,000 after 20 years? Enter just an integer representing dollars to the nearest dollar (no units)

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
65
One or more initial conditions are given for the differential equation. Use the qualitative theory of autonomous differential equations to sketch the graphs of the corresponding solution. Include a yz-graph as well as a ty-graph. Do these graphs represent: 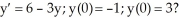
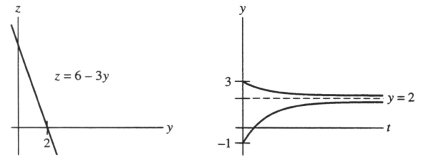
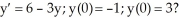


Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
66
Consider the differential equation 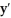 = g(y) where g(y) is the function whose graph is shown below:
= g(y) where g(y) is the function whose graph is shown below: 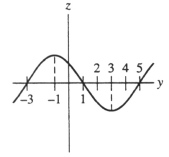
Indicate whether the following statements are true or false.
Let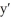 =
= 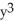 . Which of the following properties hold for the solution y = f(t) determined by the initial condition y(0) = -2? (I) It is always increasing.
. Which of the following properties hold for the solution y = f(t) determined by the initial condition y(0) = -2? (I) It is always increasing.
(II) It has an inflection point.
(III) It is always concave down.
A) I only
B) I and II
C) II only
D) III only
E) none of these
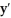 = g(y) where g(y) is the function whose graph is shown below:
= g(y) where g(y) is the function whose graph is shown below: 
Indicate whether the following statements are true or false.
Let
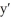 =
= 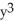 . Which of the following properties hold for the solution y = f(t) determined by the initial condition y(0) = -2? (I) It is always increasing.
. Which of the following properties hold for the solution y = f(t) determined by the initial condition y(0) = -2? (I) It is always increasing.(II) It has an inflection point.
(III) It is always concave down.
A) I only
B) I and II
C) II only
D) III only
E) none of these

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
67
Suppose that $1000 is deposited in a savings account that pays 6% annual interest compounded continuously. At what rate (in dollars per year) is it earning interest after 5 years? Enter just an integer representing the amount to the nearest dollar (no units).

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
68
Consider the differential equation 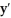 = g(y) where g(y) is the function whose graph is shown below:
= g(y) where g(y) is the function whose graph is shown below: 
Indicate whether the following statements are true or false.
For what y value(s) does a solution of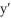 =
= 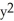 - 3y + 2 have inflection points?
- 3y + 2 have inflection points?
A) y = 2
B) y = 0
C) y = 2 and y = 1
D) y =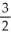
E) none of these
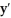 = g(y) where g(y) is the function whose graph is shown below:
= g(y) where g(y) is the function whose graph is shown below: 
Indicate whether the following statements are true or false.
For what y value(s) does a solution of
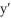 =
= 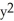 - 3y + 2 have inflection points?
- 3y + 2 have inflection points?A) y = 2
B) y = 0
C) y = 2 and y = 1
D) y =
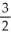
E) none of these

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
69
Suppose the following is a graph of z = g(y). 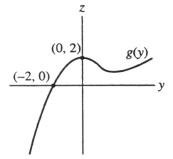 Which of the following can then be said about the solution y = f(t) to the initial value problem
Which of the following can then be said about the solution y = f(t) to the initial value problem  ?
?
(I) f(t) is an increasing function
(II) f(t) is always positive
(III) f(t) has an inflection point when y = 2.
A) III only
B) I, II, and III
C) I only
D) II only
E) I and III
 Which of the following can then be said about the solution y = f(t) to the initial value problem
Which of the following can then be said about the solution y = f(t) to the initial value problem  ?
? (I) f(t) is an increasing function
(II) f(t) is always positive
(III) f(t) has an inflection point when y = 2.
A) III only
B) I, II, and III
C) I only
D) II only
E) I and III

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
70
A nutritionist proposes the following model for weight loss on a program she is developing: 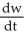 + 0.006w =
+ 0.006w = 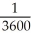 C where w(t) is a person's weight (in pounds) after t days of consuming exactly C calories per day. A person weighing 180 pounds goes on this diet program consuming 2400 calories per day. Use the above model to predict how long will it take this person to lose 15 pounds.
C where w(t) is a person's weight (in pounds) after t days of consuming exactly C calories per day. A person weighing 180 pounds goes on this diet program consuming 2400 calories per day. Use the above model to predict how long will it take this person to lose 15 pounds.
A) 41 days
B) 37 days
C) 39 days
D) 35 days
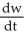 + 0.006w =
+ 0.006w = 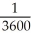 C where w(t) is a person's weight (in pounds) after t days of consuming exactly C calories per day. A person weighing 180 pounds goes on this diet program consuming 2400 calories per day. Use the above model to predict how long will it take this person to lose 15 pounds.
C where w(t) is a person's weight (in pounds) after t days of consuming exactly C calories per day. A person weighing 180 pounds goes on this diet program consuming 2400 calories per day. Use the above model to predict how long will it take this person to lose 15 pounds.A) 41 days
B) 37 days
C) 39 days
D) 35 days

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
71
Consider the differential equation 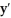 = g(y) where g(y) is the function whose graph is shown below:
= g(y) where g(y) is the function whose graph is shown below: 
Indicate whether the following statements are true or false.
y = -3, y = 1, and y = 5 are the constant solutions to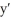 = g(y).
= g(y).
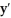 = g(y) where g(y) is the function whose graph is shown below:
= g(y) where g(y) is the function whose graph is shown below: 
Indicate whether the following statements are true or false.
y = -3, y = 1, and y = 5 are the constant solutions to
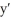 = g(y).
= g(y).
Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
72
Consider the differential equation 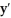 = g(y) where g(y) is the function whose graph is shown below:
= g(y) where g(y) is the function whose graph is shown below: 
Indicate whether the following statements are true or false.
Let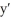 = 2 - y. Which of the following properties hold for the solution y = f(t) determined by the initial condition y(0) = 1? (I) It is always concave down.
= 2 - y. Which of the following properties hold for the solution y = f(t) determined by the initial condition y(0) = 1? (I) It is always concave down.
(II) It is a constant solution.
(III) It is always decreasing.
A) I only
B) III only
C) I and III
D) II only
E) none of these
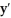 = g(y) where g(y) is the function whose graph is shown below:
= g(y) where g(y) is the function whose graph is shown below: 
Indicate whether the following statements are true or false.
Let
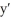 = 2 - y. Which of the following properties hold for the solution y = f(t) determined by the initial condition y(0) = 1? (I) It is always concave down.
= 2 - y. Which of the following properties hold for the solution y = f(t) determined by the initial condition y(0) = 1? (I) It is always concave down.(II) It is a constant solution.
(III) It is always decreasing.
A) I only
B) III only
C) I and III
D) II only
E) none of these

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
73
One or more initial conditions are given for the differential equation. Use the qualitative theory of autonomous differential equations to sketch the graphs of the corresponding solution. Include a yz-graph as well as a ty-graph. 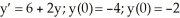 Do these graphs represent the situation?
Do these graphs represent the situation? 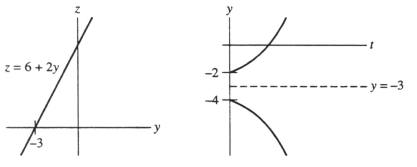
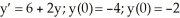 Do these graphs represent the situation?
Do these graphs represent the situation? 

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
74
There is a differential equation that is a mathematical model of the situation in which the time rate of change in the population of a certain organism is proportional to the product of the current population and the difference between the current population and the limiting factor of 100,000. Is this the equation 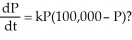
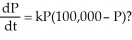

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
75
Consider the differential equation 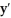 = g(y) where g(y) is the function whose graph is shown below:
= g(y) where g(y) is the function whose graph is shown below: 
Indicate whether the following statements are true or false.
y = 2 is the only constant solution of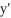 = g(y) .
= g(y) .
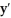 = g(y) where g(y) is the function whose graph is shown below:
= g(y) where g(y) is the function whose graph is shown below: 
Indicate whether the following statements are true or false.
y = 2 is the only constant solution of
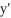 = g(y) .
= g(y) .
Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
76
Suppose 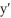 = ky + b and the graphs of several solutions of the differential equation are as below:
= ky + b and the graphs of several solutions of the differential equation are as below: 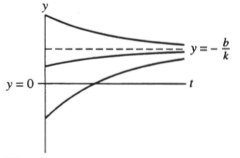 Then (I) k is negative.
Then (I) k is negative.
(II) k is positive.
(III) b is positive.
(IV) b is negative.
A) II and IV
B) I and IV
C) II and III
D) I and III
E) not enough information given
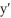 = ky + b and the graphs of several solutions of the differential equation are as below:
= ky + b and the graphs of several solutions of the differential equation are as below:  Then (I) k is negative.
Then (I) k is negative.(II) k is positive.
(III) b is positive.
(IV) b is negative.
A) II and IV
B) I and IV
C) II and III
D) I and III
E) not enough information given

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
77
Consider the differential equation 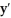 = g(y) where g(y) is the function whose graph is shown below:
= g(y) where g(y) is the function whose graph is shown below: 
Indicate whether the following statements are true or false.
If the initial value of y(0) is greater than 6, then the corresponding solution will be an increasing function.
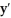 = g(y) where g(y) is the function whose graph is shown below:
= g(y) where g(y) is the function whose graph is shown below: 
Indicate whether the following statements are true or false.
If the initial value of y(0) is greater than 6, then the corresponding solution will be an increasing function.

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
78
Consider the differential equation 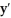 = g(y) where g(y) is the function whose graph is shown below:
= g(y) where g(y) is the function whose graph is shown below: 
Indicate whether the following statements are true or false.
If the initial value of y(0) is 3, then the corresponding solution has an inflection point.
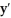 = g(y) where g(y) is the function whose graph is shown below:
= g(y) where g(y) is the function whose graph is shown below: 
Indicate whether the following statements are true or false.
If the initial value of y(0) is 3, then the corresponding solution has an inflection point.

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
79
Suppose the graph below gives a solution to the differential equation 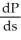 = g(P) where P is the price of a product and s is the weekly sales.
= g(P) where P is the price of a product and s is the weekly sales. 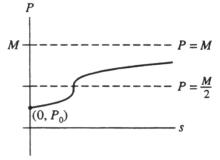 Which of the following statements is/are true?
Which of the following statements is/are true?
(I) g(M) = 0
(II)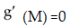
(III)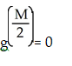
(IV) g(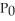 ) > 0
) > 0
A) I only
B) IV only
C) I, III, and IV
D) I and IV
E) I, II, and IV
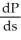 = g(P) where P is the price of a product and s is the weekly sales.
= g(P) where P is the price of a product and s is the weekly sales.  Which of the following statements is/are true?
Which of the following statements is/are true? (I) g(M) = 0
(II)
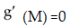
(III)
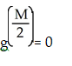
(IV) g(
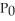 ) > 0
) > 0A) I only
B) IV only
C) I, III, and IV
D) I and IV
E) I, II, and IV

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck
80
Consider the differential equation 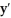 = g(y) where g(y) is the function whose graph is shown below:
= g(y) where g(y) is the function whose graph is shown below: 
Indicate whether the following statements are true or false.
If the initial value of y(0) is 2, then the corresponding solution has an inflection point.
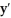 = g(y) where g(y) is the function whose graph is shown below:
= g(y) where g(y) is the function whose graph is shown below: 
Indicate whether the following statements are true or false.
If the initial value of y(0) is 2, then the corresponding solution has an inflection point.

Unlock Deck
Unlock for access to all 126 flashcards in this deck.
Unlock Deck
k this deck


