Deck 9: Rotation of Rigid Bodies
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/26
Play
Full screen (f)
Deck 9: Rotation of Rigid Bodies
1
A machinist turns the power on to a grinding wheel, which is at rest at time t = 0.00 s. The wheel accelerates uniformly for 10 s and reaches the operating angular velocity of 25 rad/s. The wheel is run at that angular velocity for 37 s and then power is shut off. The wheel decelerates uniformly at 1.5 rad/s2 until the wheel stops. In this situation, the time interval of angular deceleration (slowing down) is closest to:
A) 17 s
B) 15 s
C) 19 s
D) 21 s
E) 23 s
A) 17 s
B) 15 s
C) 19 s
D) 21 s
E) 23 s
17 s
2
A turbine blade rotates with angular velocity ω(t) = 2.00 rad/s- 2.1.00 rad/s3 t2. What is the angular acceleration of the blade at t = 9.1 s?
A) -38.2 rad/s2
B) -19.1 rad/s2
C) -86.0 rad/s2
D) -36.2 rad/s2
E) -172 rad/s2
A) -38.2 rad/s2
B) -19.1 rad/s2
C) -86.0 rad/s2
D) -36.2 rad/s2
E) -172 rad/s2
-38.2 rad/s2
3
A piece of thin uniform wire of mass m and length 3b is bent into an equilateral triangle. Find the moment of inertia of the wire triangle about an axis perpendicular to the plane of the triangle and passing through one of its vertices.
A)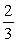 mb2
mb2
B)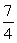 mb2
mb2
C)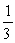 mb2
mb2
D)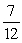 mb2
mb2
E)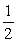 mb2
mb2
A)
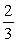 mb2
mb2B)
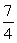 mb2
mb2C)
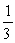 mb2
mb2D)
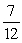 mb2
mb2E)
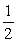 mb2
mb2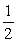 mb2
mb2 4
A uniform solid sphere has a moment of inertia I about an axis tangent to its surface. What is the moment of inertia of this sphere about an axis through its center?
A) 1/7 I
B) 2/7 I
C) 2/5 I
D) 3/5 I
E) 7/5 I
A) 1/7 I
B) 2/7 I
C) 2/5 I
D) 3/5 I
E) 7/5 I

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
5
As you are leaving a building, the door opens outward. If the hinges on the door are on your right, what is the direction of the angular velocity of the door as you open it?
A) up
B) down
C) to your left
D) to your right
E) forwards
A) up
B) down
C) to your left
D) to your right
E) forwards

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
6
A 4.50-kg wheel that is 34.5 cm in diameter rotates through an angle of 13.8 rad as it slows down uniformly from 22.0 rad/s to 13.5 rad/s. What is the magnitude of the angular acceleration of the wheel?
A) 0.616 rad/s2
B) 5.45 rad/s2
C) 111 rad/s2
D) 22.5 rad/s2
E) 10.9 rad/s2
A) 0.616 rad/s2
B) 5.45 rad/s2
C) 111 rad/s2
D) 22.5 rad/s2
E) 10.9 rad/s2

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
7
The angular acceleration of a wheel is given in rad/s2 by 45t3 - 11t4 where t is in seconds. If the wheel starts from rest at t = 0.00 s, when is the next time the wheel is at rest?
A) 5.1 s
B) 8.4 s
C) 6.9 s
D) 3.6 s
A) 5.1 s
B) 8.4 s
C) 6.9 s
D) 3.6 s

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
8
A 1.15-kg grinding wheel 22.0 cm in diameter is spinning counterclockwise at a rate of 20.0 revolutions per second. When the power to the grinder is turned off, the grinding wheel slows with constant angular acceleration and takes 80.0 s to come to a rest.
(a) What was the angular acceleration (in rad/s2) of the grinding wheel as it came to rest if we take a counterclockwise rotation as positive?
(b) How many revolutions did the wheel make during the time it was coming to rest?
(a) What was the angular acceleration (in rad/s2) of the grinding wheel as it came to rest if we take a counterclockwise rotation as positive?
(b) How many revolutions did the wheel make during the time it was coming to rest?

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
9
The angular velocity of a 755-g wheel 15.0 cm in diameter is given by the equation ω(t) = (2.00 rad/s2)t + (1.00 rad/s4)t3.
(a) Through how many radians does the wheel turn during the first 2.00 s of its motion?
(b) What is the angular acceleration (in rad/s2) of the wheel at the end of the first 2.00 s of its motion?
(a) Through how many radians does the wheel turn during the first 2.00 s of its motion?
(b) What is the angular acceleration (in rad/s2) of the wheel at the end of the first 2.00 s of its motion?

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
10
A 1.25-kg ball begins rolling from rest with constant angular acceleration down a hill. If it takes 3.60 s for it to make the first complete revolution, how long will it take to make the next complete revolution?

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
11
A dumbbell-shaped object is composed by two equal masses, m, connected by a rod of negligible mass and length r. If I1 is the moment of inertia of this object with respect to an axis passing through the center of the rod and perpendicular to it and I2 is the moment of inertia with respect to an axis passing through one of the masses, it follows that
A) I1 = I2.
B) I1 > I2.
C) I2 > I1.
A) I1 = I2.
B) I1 > I2.
C) I2 > I1.

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
12
In the figure, point P is at rest when it is on the x-axis. The time t, when P returns to the original position on the x-axis, is closest to 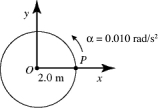
A) 13 s.
B) 18 s.
C) 25 s.
D) 35 s.
E) 50 s.

A) 13 s.
B) 18 s.
C) 25 s.
D) 35 s.
E) 50 s.

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
13
When a rigid body rotates about a fixed axis, all the points in the body have the same
A) tangential speed.
B) angular acceleration.
C) tangential acceleration.
D) linear displacement.
E) centripetal acceleration.
A) tangential speed.
B) angular acceleration.
C) tangential acceleration.
D) linear displacement.
E) centripetal acceleration.

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
14
In the figure, point P is at rest when it is on the x-axis. The linear speed of point P when it reaches the y-axis is closest to 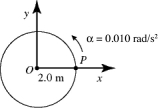
A) 0.18 m/s.
B) 0.24 m/s.
C) 0.35 m/s.
D) 0.49 m/s.
E) 0.71 m/s.

A) 0.18 m/s.
B) 0.24 m/s.
C) 0.35 m/s.
D) 0.49 m/s.
E) 0.71 m/s.

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
15
A slender uniform rod 100.00 cm long is used as a meter stick. Two parallel axes that are perpendicular to the rod are considered. The first axis passes through the 50-cm mark and the second axis passes through the 30-cm mark. What is the ratio of the moment of inertia through the second axis to the moment of inertia through the first axis?
A) I2/I1 = 1.5
B) I2/I1 = 1.7
C) I2/I1 = 1.9
D) I2/I1 = 2.1
E) I2/I1 = 2.3
A) I2/I1 = 1.5
B) I2/I1 = 1.7
C) I2/I1 = 1.9
D) I2/I1 = 2.1
E) I2/I1 = 2.3

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
16
In the figure, a weightlifter's barbell consists of two identical uniform spherical masses each with radius 0.17 m and mass of 50 kg. The weights are connected by a 0.96-m uniform steel rod with a mass of 12 kg. Find the moment of inertia of the barbell about the axis through the center (see figure). 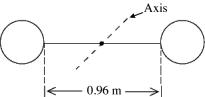


Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
17
When a 2.75-kg fan, having blades 18.5 cm long, is turned off, its angular speed decreases uniformly from 10.0 rad/s to 6.30 rad/s in 5.00 s.
(a) What is the magnitude of the angular acceleration of the fan?
(b) Through what angle (in degrees) does it turn while it is slowing down during the 5.00 s?
(c) If its angular acceleration does not change, how long after it is turned off does it take the fan to stop.
(a) What is the magnitude of the angular acceleration of the fan?
(b) Through what angle (in degrees) does it turn while it is slowing down during the 5.00 s?
(c) If its angular acceleration does not change, how long after it is turned off does it take the fan to stop.

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
18
A horizontal disk rotates about a vertical axis through its center. Point P is midway between the center and the rim of the disk, and point Q is on the rim. If the disk turns with constant angular velocity, which of the following statements about it are true? (There may be more than one correct choice.)
A) P and Q have the same linear acceleration.
B) Q is moving twice as fast as P.
C) The linear acceleration of Q is twice as great as the linear acceleration of P.
D) The linear acceleration of P is twice as great as the linear acceleration of Q.
E) The angular velocity of Q is twice as great as the angular velocity of P.
A) P and Q have the same linear acceleration.
B) Q is moving twice as fast as P.
C) The linear acceleration of Q is twice as great as the linear acceleration of P.
D) The linear acceleration of P is twice as great as the linear acceleration of Q.
E) The angular velocity of Q is twice as great as the angular velocity of P.

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
19
When you ride a bicycle, in what direction is the angular velocity of the wheels?
A) to your left
B) to your right
C) forwards
D) backwards
E) up
A) to your left
B) to your right
C) forwards
D) backwards
E) up

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
20
A 3.45-kg centrifuge takes 100 s to spin up from rest to its final angular speed with constant angular acceleration. A point located 8.00 cm from the axis of rotation of the centrifuge moves with a speed of 150 m/s when the centrifuge is at full speed.
(a) What is the angular acceleration (in rad/s2) of the centrifuge as it spins up?
(b) How many revolutions does the centrifuge make as it goes from rest to its final angular speed?
(a) What is the angular acceleration (in rad/s2) of the centrifuge as it spins up?
(b) How many revolutions does the centrifuge make as it goes from rest to its final angular speed?

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
21
In the figure, two blocks, of masses 2.00 kg and 3.00 kg, are connected by a light string that passes over a frictionless pulley of moment of inertia 0.00400 kg · m2 and radius 5.00 cm. The coefficient of friction for the tabletop is 0.300. The blocks are released from rest. Using energy methods, find the speed of the upper block just as it has moved 0.600 m. 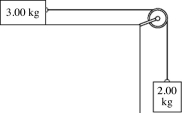
A) 1.22 m/s
B) 5.44 m/s
C) 3.19 m/s
D) 1.95 m/s
E) 1.40 m/s

A) 1.22 m/s
B) 5.44 m/s
C) 3.19 m/s
D) 1.95 m/s
E) 1.40 m/s

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
22
While spinning down from 500.0 rpm to rest, a solid uniform flywheel does 5.1 kJ of work. If the radius of the disk is 1.2 m, what is its mass?
A) 5.2 kg
B) 4.4 kg
C) 6.0 kg
D) 6.8 kg
A) 5.2 kg
B) 4.4 kg
C) 6.0 kg
D) 6.8 kg

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
23
An extremely light rod 1.00 m long has a 2.00-kg mass attached to one end and a 3.00-kg mass attached to the other. The system rotates at a constant angular speed about a fixed axis perpendicular to the rod that passes through the rod 30.0 cm from the end with the 3.00-kg mass attached. The kinetic energy of the system is measured to be 100.0 J.
(a) What is the moment of inertia of this system about the fixed axis?
(b) What is the angular speed (in revolutions per second) of this system?
(a) What is the moment of inertia of this system about the fixed axis?
(b) What is the angular speed (in revolutions per second) of this system?

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
24
A futuristic design for a car is to have a large solid disk-shaped flywheel within the car storing kinetic energy. The uniform flywheel has mass 370 kg with a radius of 0.500 m and can rotate up to 230 rev/s. Assuming all of this stored kinetic energy could be transferred to the linear velocity of the 1600-kg car, find the maximum attainable speed of the car.

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
25
A uniform solid sphere of mass M and radius R rotates with an angular speed ω about an axis through its center. A uniform solid cylinder of mass M, radius R, and length 2R rotates through an axis running through the central axis of the cylinder. What must be the angular speed of the cylinder so it will have the same rotational kinetic energy as the sphere?
A) 2ω/5
B)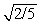 ω
ω
C) 4ω/5
D) 2ω/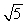
E) ω/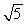
A) 2ω/5
B)
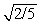 ω
ωC) 4ω/5
D) 2ω/
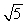
E) ω/
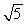

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck
26
At any angular speed, a certain uniform solid sphere of diameter D has half as much rotational kinetic energy as a certain uniform thin-walled hollow sphere of the same diameter when both are spinning about an axis through their centers. If the mass of the solid sphere is M, the mass of the hollow sphere is
A) 3/5 M.
B) 5/3 M.
C) 5/6 M.
D) 6/5 M.
E) 2 M.
A) 3/5 M.
B) 5/3 M.
C) 5/6 M.
D) 6/5 M.
E) 2 M.

Unlock Deck
Unlock for access to all 26 flashcards in this deck.
Unlock Deck
k this deck


