Deck 49: The Inverse of a Square Matrix
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/59
Play
Full screen (f)
Deck 49: The Inverse of a Square Matrix
1
Find the inverse of the matrix (if it exists). 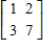
A)
B)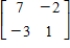
C)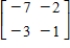
D)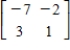
E)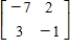
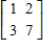
A)

B)
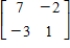
C)
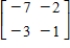
D)
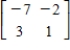
E)
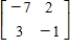
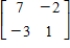
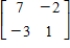
2
Use the inverse formula 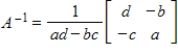 to find the inverse of the 2×2 matrix (if it exists).
to find the inverse of the 2×2 matrix (if it exists). 
A)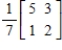
B)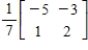
C)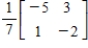
D)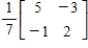
E)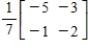
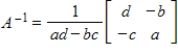 to find the inverse of the 2×2 matrix (if it exists).
to find the inverse of the 2×2 matrix (if it exists). 
A)
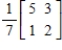
B)
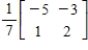
C)
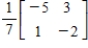
D)
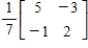
E)
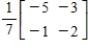
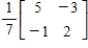
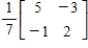
3
Solve the system of linear equations. 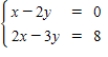
A)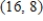
B)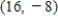
C)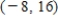
D)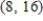
E)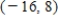
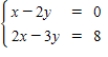
A)
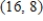
B)
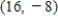
C)
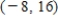
D)
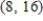
E)
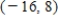
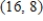
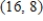
4
Use the inverse formula 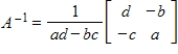 to find the inverse of the 2×2 matrix (if it exists).
to find the inverse of the 2×2 matrix (if it exists). 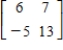
A)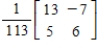
B)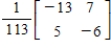
C)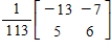
D)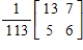
E)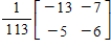
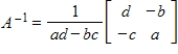 to find the inverse of the 2×2 matrix (if it exists).
to find the inverse of the 2×2 matrix (if it exists). 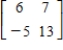
A)
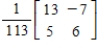
B)
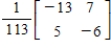
C)
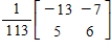
D)
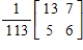
E)
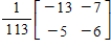

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
5
Use the inverse formula 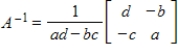 to find the inverse of the matrix (if it exists).
to find the inverse of the matrix (if it exists). 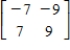
A)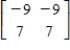
B)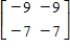
C)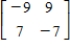
D)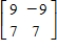
E)Does not exist
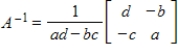 to find the inverse of the matrix (if it exists).
to find the inverse of the matrix (if it exists). 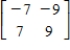
A)
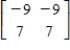
B)
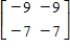
C)
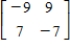
D)
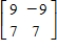
E)Does not exist

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
6
Use the inverse formula 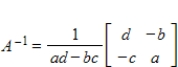 to find the inverse of the 2×2 matrix (if it exists).
to find the inverse of the 2×2 matrix (if it exists). 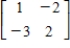
A)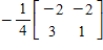
B)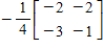
C)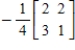
D)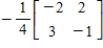
E)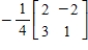
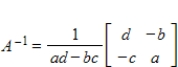 to find the inverse of the 2×2 matrix (if it exists).
to find the inverse of the 2×2 matrix (if it exists). 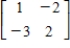
A)
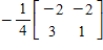
B)
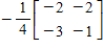
C)
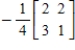
D)
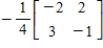
E)
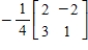

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
7
Find the inverse of the matrix (if it exists). 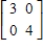
A)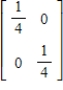
B)
C)
D)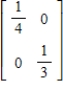
E)

A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
8
Find the inverse of the matrix (if it exists). 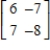
A)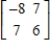
B)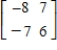
C)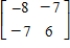
D)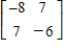
E)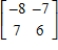
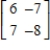
A)
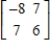
B)
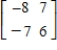
C)
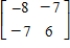
D)
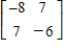
E)
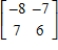

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
9
Use the inverse formula 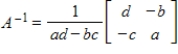 to find the inverse of the 2×2 matrix (if it exists).
to find the inverse of the 2×2 matrix (if it exists). 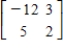
A)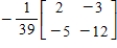
B)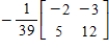
C)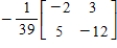
D)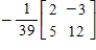
E)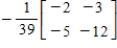
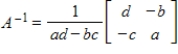 to find the inverse of the 2×2 matrix (if it exists).
to find the inverse of the 2×2 matrix (if it exists). 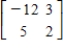
A)
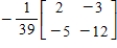
B)
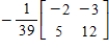
C)
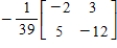
D)
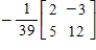
E)
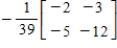

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
10
Find the inverse of the matrix (if it exists). 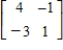
A)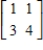
B)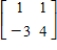
C)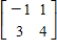
D)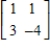
E)Does not exist
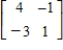
A)
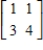
B)
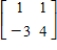
C)
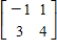
D)
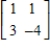
E)Does not exist

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
11
Use an inverse matrix to solve (if possible)the system of linear equations. 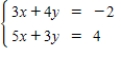
A)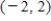
B)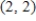
C)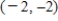
D)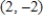
E)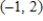
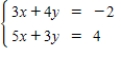
A)
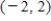
B)
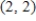
C)
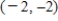
D)
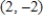
E)
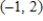

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
12
Find the inverse of the matrix (if it exists). 
A)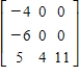
B)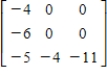
C)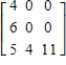
D)
E)Does not exist

A)

B)
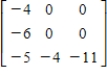
C)
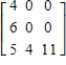
D)

E)Does not exist

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
13
Solve the system of linear equations. 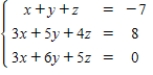
A)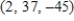
B)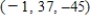
C)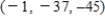
D)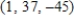
E)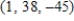
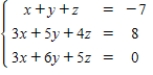
A)
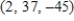
B)
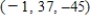
C)
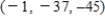
D)
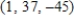
E)
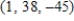

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
14
Solve the system of linear equations. 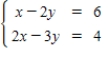
A)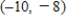
B)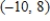
C)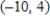
D)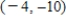
E)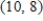
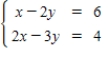
A)
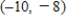
B)
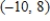
C)
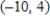
D)
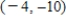
E)
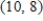

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
15
Find the inverse of the matrix (if it exists). 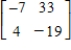
A)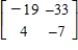
B)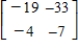
C)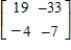
D)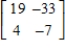
E)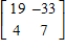
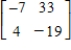
A)
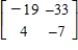
B)
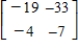
C)
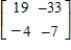
D)
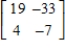
E)
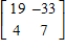

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
16
Solve the system of linear equations. 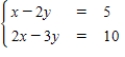
A)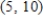
B)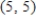
C)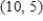
D)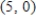
E)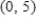
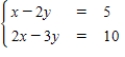
A)
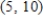
B)
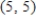
C)
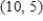
D)
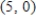
E)
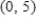

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
17
Solve the system of linear equations. 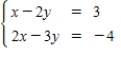
A)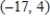
B)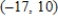
C)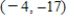
D)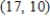
E)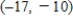
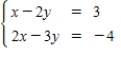
A)
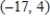
B)
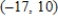
C)
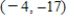
D)
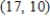
E)
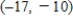

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
18
Find the inverse of the matrix (if it exists). 
A)
B)
C)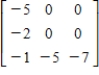
D)
E)Does not exist

A)

B)

C)
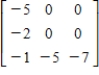
D)

E)Does not exist

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
19
Solve the system of linear equations. 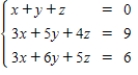
A)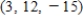
B)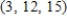
C)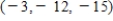
D)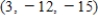
E)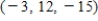
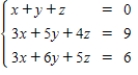
A)
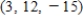
B)
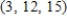
C)
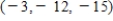
D)
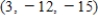
E)
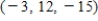

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
20
Use an inverse matrix to solve (if possible)the system of linear equations. 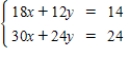
A)( ,
,  )
)
B)( 4, )
)
C)( ,
,  )
)
D)( ,
,  )
)
E)( ,3 )
,3 )
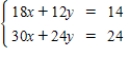
A)(
 ,
,  )
)B)( 4,
 )
)C)(
 ,
,  )
)D)(
 ,
,  )
)E)(
 ,3 )
,3 )
Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
21
The table shows the enrollment projections (in millions)for public universities in the United States for the years 2010 through 2012.
Year
Enrollment projections
2010
13)83
2011
14)07
2012
14)23
The data can be modeled by the quadratic function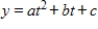 .Create a system of linear equations for the data.Let t represent the year,with t = 10 corresponding to 2010.
.Create a system of linear equations for the data.Let t represent the year,with t = 10 corresponding to 2010.
A)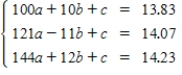
B)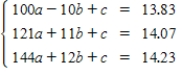
C)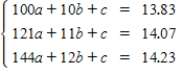
D)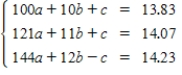
E)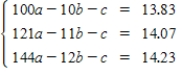
Year
Enrollment projections
2010
13)83
2011
14)07
2012
14)23
The data can be modeled by the quadratic function
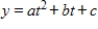 .Create a system of linear equations for the data.Let t represent the year,with t = 10 corresponding to 2010.
.Create a system of linear equations for the data.Let t represent the year,with t = 10 corresponding to 2010.A)
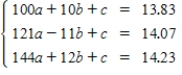
B)
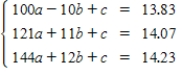
C)
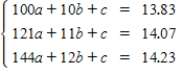
D)
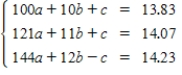
E)
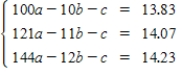

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
22
Consider a person who invests in AAA-rated bonds,A-rated bonds,and B-rated bonds.The average yields are 6.5% on AAA bonds,7% on A bonds,and 9% on B bonds.The person invests twice as much in B bonds as in A bonds.Let x,y and z represent the amounts invested in AAA,A,and B bonds,respectively. Total Investment
Annual Return
$12,000
890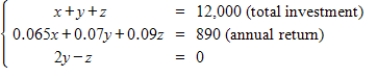 Use the inverse of the coefficient matrix of this system to find the amount invested in each type of bond.
Use the inverse of the coefficient matrix of this system to find the amount invested in each type of bond.
A)$7,000 in AAA-rated bonds $2,000 in A-rated bonds
$4,000 in B-rated bonds
B)$5,000 in AAA-rated bonds $7,000 in A-rated bonds
$3,000 in B-rated bonds
C)$5,000 in AAA-rated bonds $6,000 in A-rated bonds
$4,000 in B-rated bonds
D)$3,000 in AAA-rated bonds $2,000 in A-rated bonds
$6,000 in B-rated bonds
E)$6,000 in AAA-rated bonds $2,000 in A-rated bonds
$4,000 in B-rated bonds
Annual Return
$12,000
890
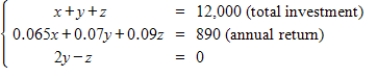 Use the inverse of the coefficient matrix of this system to find the amount invested in each type of bond.
Use the inverse of the coefficient matrix of this system to find the amount invested in each type of bond.A)$7,000 in AAA-rated bonds $2,000 in A-rated bonds
$4,000 in B-rated bonds
B)$5,000 in AAA-rated bonds $7,000 in A-rated bonds
$3,000 in B-rated bonds
C)$5,000 in AAA-rated bonds $6,000 in A-rated bonds
$4,000 in B-rated bonds
D)$3,000 in AAA-rated bonds $2,000 in A-rated bonds
$6,000 in B-rated bonds
E)$6,000 in AAA-rated bonds $2,000 in A-rated bonds
$4,000 in B-rated bonds

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
23
Find the inverse of the matrix 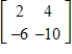 .
.
A)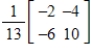
B)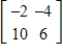
C)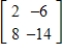
D)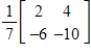
E)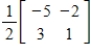
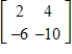 .
.A)
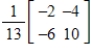
B)
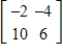
C)
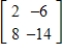
D)
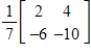
E)
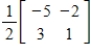

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
24
Find the inverse of the matrix 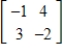 (if it exists).
(if it exists).
A)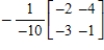
B)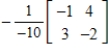
C)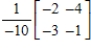
D)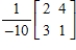
E)does not exist
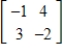 (if it exists).
(if it exists).A)
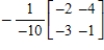
B)
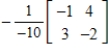
C)
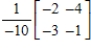
D)
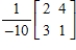
E)does not exist

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
25
A small home business creates muffins,bones,and cookies for dogs.In addition to other ingredients,each muffin requires 2 units of beef,3 units of chicken,and 2 units of liver.Each bone requires 1 unit of beef,1 unit of chicken,and 1 unit of liver.Each cookie requires 2 units of beef,1 unit of chicken,and 1.5 units of liver.Find the numbers of muffins,bones,and cookies that the company can create with the given amounts of ingredients.
875 units of beef
830 units of chicken
850 units of liver
A)765 muffins,5 bones,50 cookies
B)50 muffins,765 bones,50 cookies
C)5 muffins,765 bones,50 cookies
D)50 muffins,765 bones,5 cookies
E)5 muffins,5 bones,830 cookies
875 units of beef
830 units of chicken
850 units of liver
A)765 muffins,5 bones,50 cookies
B)50 muffins,765 bones,50 cookies
C)5 muffins,765 bones,50 cookies
D)50 muffins,765 bones,5 cookies
E)5 muffins,5 bones,830 cookies

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
26
A florist is creating 10 centerpieces for the tables at a wedding reception.Roses cost $2.50 each,lilies cost $8 each,and irises cost $4 each.The customer has a budget of $300 allocated for the centerpieces and wants each centerpiece to contain 12 flowers,with twice as many roses as the number of irises and lilies combined.
Write a system of linear equations that represents the situation.
A)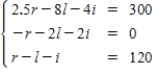
B)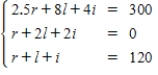
C)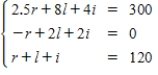
D)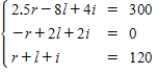
E)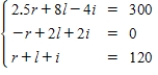
Write a system of linear equations that represents the situation.
A)
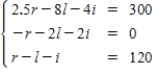
B)
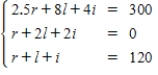
C)
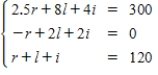
D)
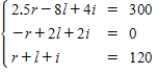
E)
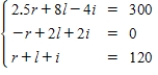

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
27
Solve the system of linear equations 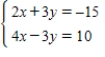 using the inverse matrix
using the inverse matrix 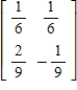
A)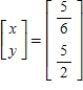
B)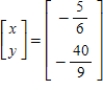
C)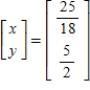
D)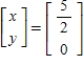
E)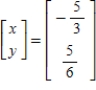
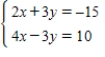 using the inverse matrix
using the inverse matrix 
A)
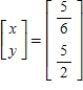
B)
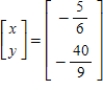
C)
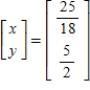
D)
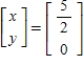
E)
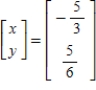

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
28
Use an inverse matrix to solve (if possible)the system of linear equations. 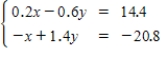
A)(-24,-31)
B)(-23,-32)
C)(-22,-32)
D)(-24,-32)
E)(-23,-30)
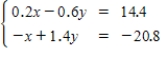
A)(-24,-31)
B)(-23,-32)
C)(-22,-32)
D)(-24,-32)
E)(-23,-30)

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
29
Use an inverse matrix to solve (if possible)the system of linear equations. 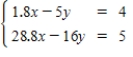
A)(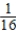 ,16)
,16)
B)(0,0)
C)(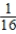 ,
, 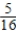 )
)
D)(16,16)
E)No solution
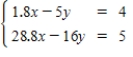
A)(
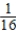 ,16)
,16)B)(0,0)
C)(
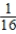 ,
, 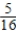 )
)D)(16,16)
E)No solution

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
30
A coffee manufacturer sells a 14-pound package that contains three flavors of coffee for $25.French vanilla coffee costs $5 per pound,hazelnut flavored coffee costs $5.50 per pound,and Swiss chocolate flavored coffee costs $6 per pound.The package contains the same amount of hazelnut as Swiss chocolate.Let f represent the number of pounds of French vanilla,h represent the number of pounds of hazelnut,and s represent the number of pounds of Swiss chocolate.
Write a system of linear equations that represents the situation.
A)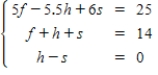
B)
C)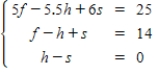
D)
E)
Write a system of linear equations that represents the situation.
A)
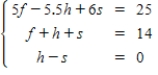
B)

C)
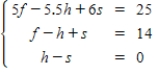
D)

E)


Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
31
Find the inverse of the matrix 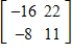 (if it exists).
(if it exists).
A)does not exist
B)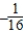
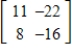
C)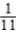
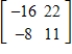
D)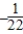
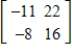
E)
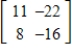
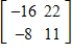 (if it exists).
(if it exists).A)does not exist
B)
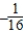
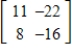
C)
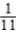
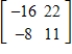
D)
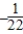
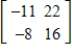
E)

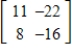

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
32
Consider a person who invests in AAA-rated bonds,A-rated bonds,and B-rated bonds.The average yields are 6.5% on AAA bonds,7% on A bonds,and 9% on B bonds.The person invests twice as much in B bonds as in A bonds.Let x,y and z represent the amounts invested in AAA,A,and B bonds,respectively. Total Investment
Annual Return
$32,000
2465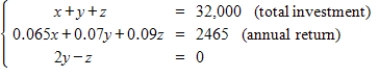 Use the inverse of the coefficient matrix of this system to find the amount invested in each type of bond.
Use the inverse of the coefficient matrix of this system to find the amount invested in each type of bond.
A)$11,000 in AAA-rated bonds $7,000 in A-rated bonds
$14,000 in B-rated bonds
B)$11,000 in AAA-rated bonds $14,000 in A-rated bonds
$7,000 in B-rated bonds
C)$14,000 in AAA-rated bonds $11,000 in A-rated bonds
$7,000 in B-rated bonds
D)$14,000 in AAA-rated bonds $7,000 in A-rated bonds
$11,000 in B-rated bonds
E)$7,000 in AAA-rated bonds $11,000 in A-rated bonds
$14,000 in B-rated bonds
Annual Return
$32,000
2465
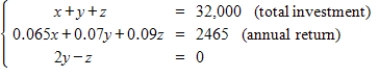 Use the inverse of the coefficient matrix of this system to find the amount invested in each type of bond.
Use the inverse of the coefficient matrix of this system to find the amount invested in each type of bond.
A)$11,000 in AAA-rated bonds $7,000 in A-rated bonds
$14,000 in B-rated bonds
B)$11,000 in AAA-rated bonds $14,000 in A-rated bonds
$7,000 in B-rated bonds
C)$14,000 in AAA-rated bonds $11,000 in A-rated bonds
$7,000 in B-rated bonds
D)$14,000 in AAA-rated bonds $7,000 in A-rated bonds
$11,000 in B-rated bonds
E)$7,000 in AAA-rated bonds $11,000 in A-rated bonds
$14,000 in B-rated bonds

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
33
A small home business creates muffins,bones,and cookies for dogs.In addition to other ingredients,each muffin requires 2 units of beef,3 units of chicken,and 2 units of liver.Each bone requires 1 unit of beef,1 unit of chicken,and 1 unit of liver.Each cookie requires 2 units of beef,1 unit of chicken,and 1.5 units of liver.Find the numbers of muffins,bones,and cookies that the company can create with the given amounts of ingredients.
900 units of beef
700 units of chicken
800 units of liver
A)200 muffins,500 bones,200 cookies
B)200 muffins,500 bones,0 cookies
C)0 muffins,0 bones,700 cookies
D)500 muffins,0 bones,200 cookies
E)0 muffins,500 bones,200 cookies
900 units of beef
700 units of chicken
800 units of liver
A)200 muffins,500 bones,200 cookies
B)200 muffins,500 bones,0 cookies
C)0 muffins,0 bones,700 cookies
D)500 muffins,0 bones,200 cookies
E)0 muffins,500 bones,200 cookies

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
34
Solve the system of linear equations 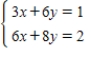 using the inverse matrix
using the inverse matrix 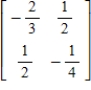
A)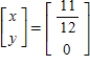
B)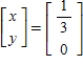
C)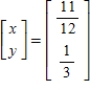
D)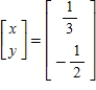
E)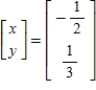
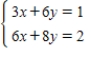 using the inverse matrix
using the inverse matrix 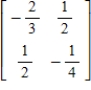
A)
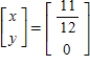
B)
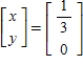
C)
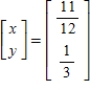
D)
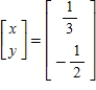
E)
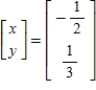

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
35
Consider a person who invests in AAA-rated bonds,A-rated bonds,and B-rated bonds.The average yields are 6.5% on AAA bonds,7% on A bonds,and 9% on B bonds.The person invests twice as much in B bonds as in A bonds.Let x,y and z represent the amounts invested in AAA,A,and B bonds,respectively. 
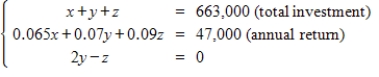 Use the inverse of the coefficient matrix of this system to find the amount invested in each type of bond.
Use the inverse of the coefficient matrix of this system to find the amount invested in each type of bond.
A)$142,000 in AAA-rated bonds $451,000 in A-rated bonds
$71,000 in B-rated bonds
B)$450,000 in AAA-rated bonds $71,000 in A-rated bonds
$142,000 in B-rated bonds
C)$143,000 in AAA-rated bonds $71,000 in A-rated bonds
$450,000 in B-rated bonds
D)$72,000 in AAA-rated bonds $450,000 in A-rated bonds
$142,000 in B-rated bonds
E)$450,000 in AAA-rated bonds $142,000 in A-rated bonds
$70,000 in B-rated bonds

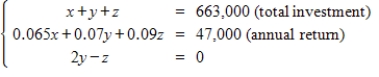 Use the inverse of the coefficient matrix of this system to find the amount invested in each type of bond.
Use the inverse of the coefficient matrix of this system to find the amount invested in each type of bond.
A)$142,000 in AAA-rated bonds $451,000 in A-rated bonds
$71,000 in B-rated bonds
B)$450,000 in AAA-rated bonds $71,000 in A-rated bonds
$142,000 in B-rated bonds
C)$143,000 in AAA-rated bonds $71,000 in A-rated bonds
$450,000 in B-rated bonds
D)$72,000 in AAA-rated bonds $450,000 in A-rated bonds
$142,000 in B-rated bonds
E)$450,000 in AAA-rated bonds $142,000 in A-rated bonds
$70,000 in B-rated bonds

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
36
Use the matrix capabilities of a graphing utility to find the inverse of the matrix 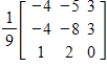 (if it exists).
(if it exists).
A)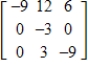
B)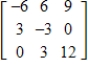
C)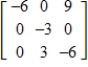
D)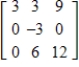
E)does not exist
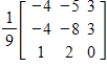 (if it exists).
(if it exists).A)
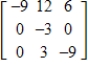
B)
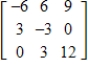
C)
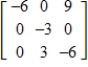
D)
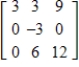
E)does not exist

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
37
A small home business creates muffins,bones,and cookies for dogs.In addition to other ingredients,each muffin requires 2 units of beef,3 units of chicken,and 2 units of liver.Each bone requires 1 unit of beef,1 unit of chicken,and 1 unit of liver.Each cookie requires 2 units of beef,1 unit of chicken,and 1.5 units of liver.Find the numbers of muffins,bones,and cookies that the company can create with the given amounts of ingredients.
3,000 units of beef
2,950 units of chicken
2,900 units of liver
A)200 muffins,2,300 bones,200 cookies
B)150 muffins,150 bones,2,950 cookies
C)200 muffins,2,300 bones,150 cookies
D)2,300 muffins,150 bones,200 cookies
E)150 muffins,2,300 bones,200 cookies
3,000 units of beef
2,950 units of chicken
2,900 units of liver
A)200 muffins,2,300 bones,200 cookies
B)150 muffins,150 bones,2,950 cookies
C)200 muffins,2,300 bones,150 cookies
D)2,300 muffins,150 bones,200 cookies
E)150 muffins,2,300 bones,200 cookies

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
38
Find the inverse of the matrix 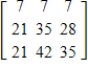 .
.
A)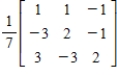
B)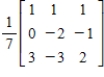
C)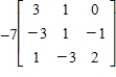
D)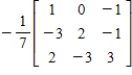
E)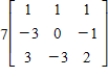
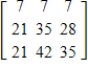 .
. A)
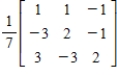
B)
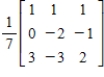
C)
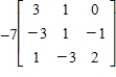
D)
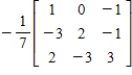
E)
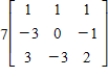

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
39
Find the inverse of the following matrix. 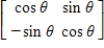
A)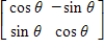
B)
C)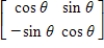
D)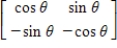
E)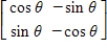
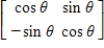
A)
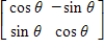
B)

C)
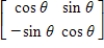
D)
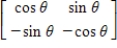
E)
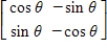

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
40
A small home business creates muffins,bones,and cookies for dogs.In addition to other ingredients,each muffin requires 2 units of beef,3 units of chicken,and 2 units of liver.Each bone requires 1 unit of beef,1 unit of chicken,and 1 unit of liver.Each cookie requires 2 units of beef,1 unit of chicken,and 1.5 units of liver.Find the numbers of muffins,bones,and cookies that the company can create with the given amounts of ingredients.
800 units of beef
750 units of chicken
725 units of liver
A)150 muffins,300 bones,150 cookies
B)150 muffins,300 bones,100 cookies
C)300 muffins,100 bones,150 cookies
D)100 muffins,300 bones,150 cookies
E)100 muffins,100 bones,750 cookies
800 units of beef
750 units of chicken
725 units of liver
A)150 muffins,300 bones,150 cookies
B)150 muffins,300 bones,100 cookies
C)300 muffins,100 bones,150 cookies
D)100 muffins,300 bones,150 cookies
E)100 muffins,100 bones,750 cookies

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
41
Solve the system of linear equations 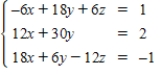 using an inverse matrix.
using an inverse matrix.
A)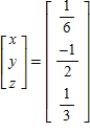
B)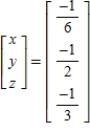
C)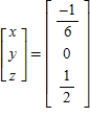
D)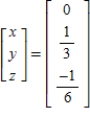
E)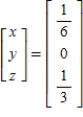
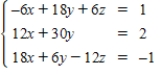 using an inverse matrix.
using an inverse matrix. A)
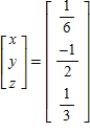
B)
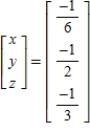
C)
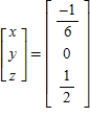
D)
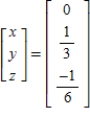
E)
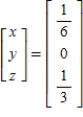

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
42
Solve the system of linear equations 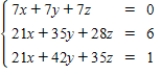 using the inverse matrix
using the inverse matrix 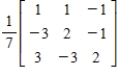 .
.
A)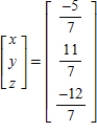
B)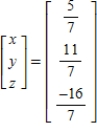
C)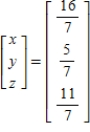
D)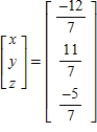
E)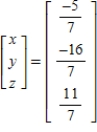
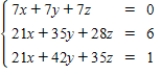 using the inverse matrix
using the inverse matrix 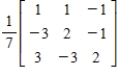 .
.A)
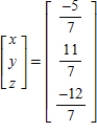
B)
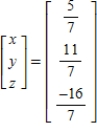
C)
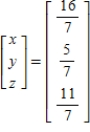
D)
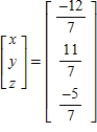
E)
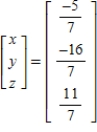

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
43
Find the inverse of A. 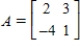
A)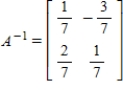
B)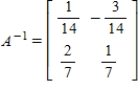
C)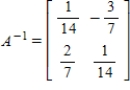
D)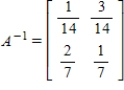
E)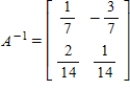
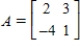
A)
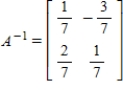
B)
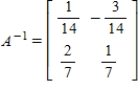
C)
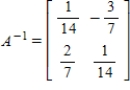
D)
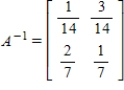
E)
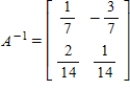

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
44
Find the inverse of the matrix. 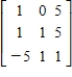
A)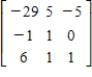
B)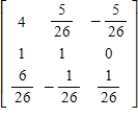
C)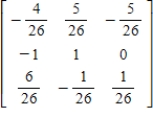
D)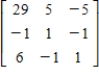
E)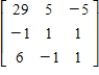
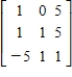
A)
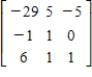
B)
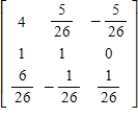
C)
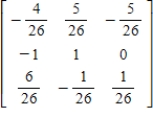
D)
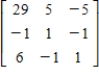
E)
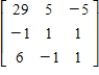

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
45
Find the inverse of the matrix 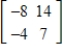 (if it exists).
(if it exists).
A)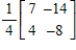
B)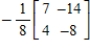
C)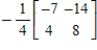
D)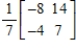
E)does not exist
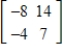 (if it exists).
(if it exists).A)
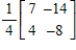
B)
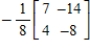
C)
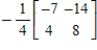
D)
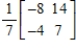
E)does not exist

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
46
Use a graphing calculator to find the inverse of the matrix. 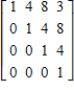
A)
B)
C)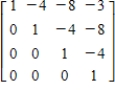
D)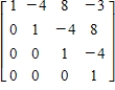
E)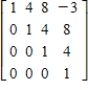

A)

B)

C)
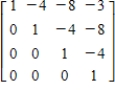
D)
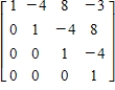
E)


Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
47
Solve the system of linear equations 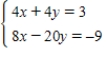 using an inverse matrix.
using an inverse matrix.
A)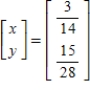
B)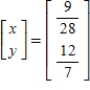
C)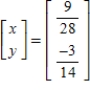
D)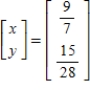
E)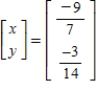
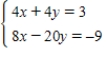 using an inverse matrix.
using an inverse matrix.A)
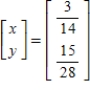
B)
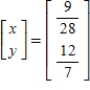
C)
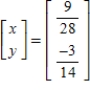
D)
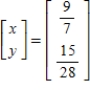
E)
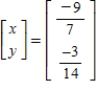

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
48
Find the inverse of the matrix. 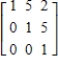
A)
B)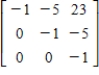
C)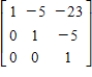
D)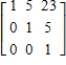
E)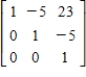
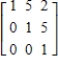
A)

B)
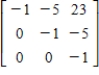
C)
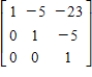
D)
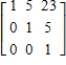
E)
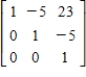

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
49
Find the inverse of A. 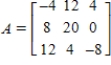
A)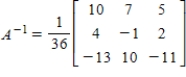
B)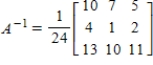
C)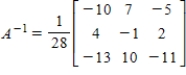
D)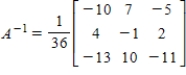
E)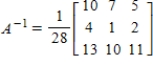
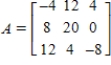
A)
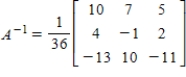
B)
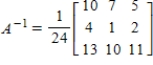
C)
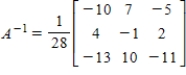
D)
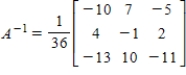
E)
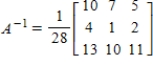

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
50
Find the inverse of the matrix. 
A)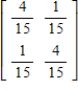
B)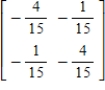
C)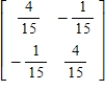
D)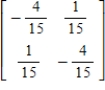
E)

A)

B)
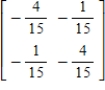
C)
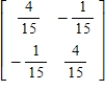
D)
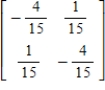
E)


Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
51
Solve the system of linear equations 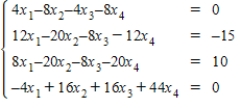 using the inverse matrix
using the inverse matrix  .
.
A)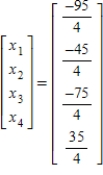
B)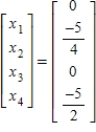
C)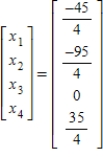
D)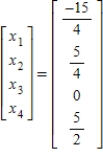
E)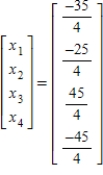
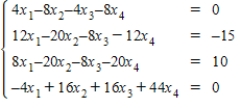 using the inverse matrix
using the inverse matrix  .
.A)
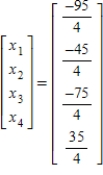
B)
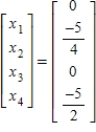
C)
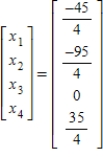
D)
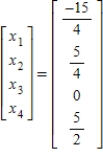
E)
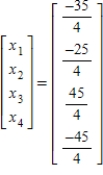

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
52
Solve the system of linear equations 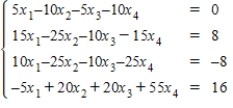 using the inverse matrix
using the inverse matrix  .
.
A)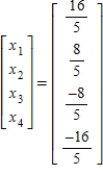
B)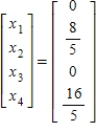
C)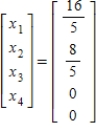
D)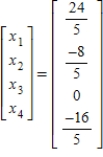
E)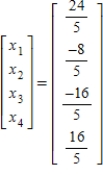
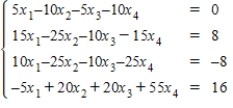 using the inverse matrix
using the inverse matrix  .
.A)
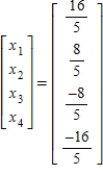
B)
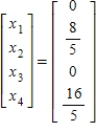
C)
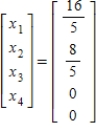
D)
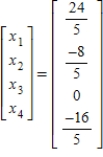
E)
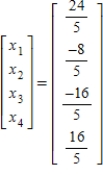

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
53
Find the inverse of the matrix 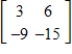 .
.
A)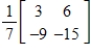
B)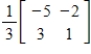
C)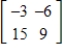
D)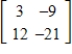
E)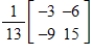
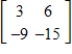 .
.A)
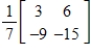
B)
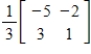
C)
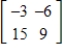
D)
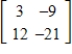
E)
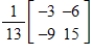

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
54
Find the inverse of the matrix  .
.
A)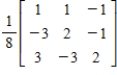
B)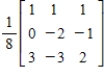
C)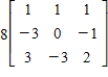
D)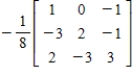
E)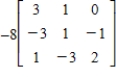
 .
.A)
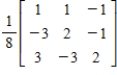
B)
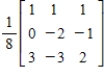
C)
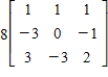
D)
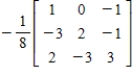
E)
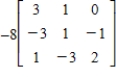

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
55
Use the matrix capabilities of a graphing utility to solve the following system of linear equations: 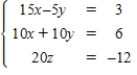
A)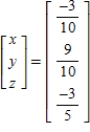
B)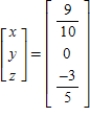
C)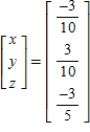
D)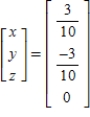
E)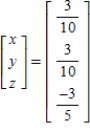
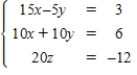
A)
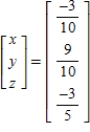
B)
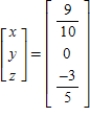
C)
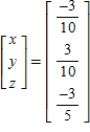
D)
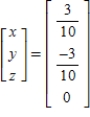
E)
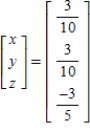

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
56
Use the matrix capabilities of a graphing utility to solve the following system of linear equations: 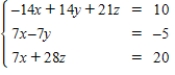
A)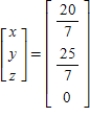
B)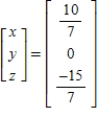
C)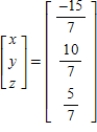
D)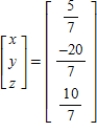
E)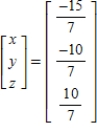
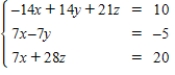
A)
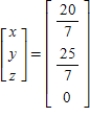
B)
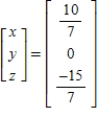
C)
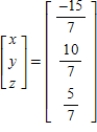
D)
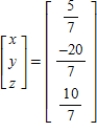
E)
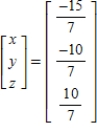

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
57
Find the inverse of the matrix 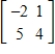 (if it exists).
(if it exists).
A)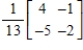
B)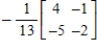
C)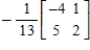
D)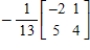
E)does not exist
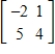 (if it exists).
(if it exists).A)
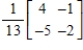
B)
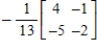
C)
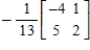
D)
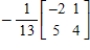
E)does not exist

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
58
Show that B is the inverse of A.Show all your work. 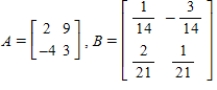
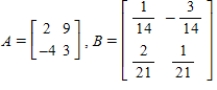

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
59
Solve the system of linear equations 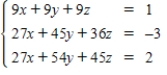 using the inverse matrix
using the inverse matrix 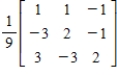 .
.
A)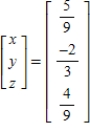
B)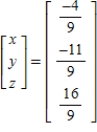
C)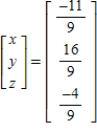
D)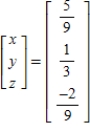
E)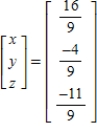
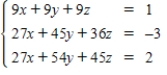 using the inverse matrix
using the inverse matrix 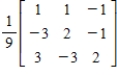 .
.A)
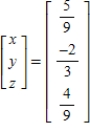
B)
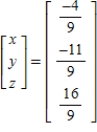
C)
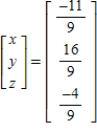
D)
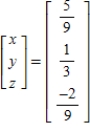
E)
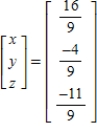

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck


