Deck 12: Chi-Square Tests
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/96
Play
Full screen (f)
Deck 12: Chi-Square Tests
1
One use of the chi-square goodness of fit test is to determine if specified multinomial probabilities in the null hypothesis is correct.
True
2
When we carry out a chi-square test of independence,in the alternative hypothesis we state that the two classifications are statistically independent.
False
3
The actual counts in the cells of a contingency table are referred to as the expected cell frequencies.
False
4
When using the chi-square goodness of fit test,if the value of the chi-square statistic is large enough,we reject the null hypothesis.

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
5
When we carry out a chi-square test of independence,the expected frequencies are based on the null hypothesis.

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
6
The trials of a multinomial probability are assumed to be dependent.

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
7
When we carry out a chi-square test of independence,if ri is row total for row i and cj is the column total for column j,then the estimated expected cell frequency corresponding to row i and column j equals (ri)(cj)/n.

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
8
In a contingency table,when all the expected frequencies equal the observed frequencies the calculated 2 statistic equals zero.

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
9
The 2 goodness of fit test requires nominative level of data.

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
10
When using chi-square goodness of fit test with multinomial probabilities,the rejection of the null hypothesis indicates that at least one of the multinomial probabilities is not equal to the value stated in the null hypothesis.

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
11
When we carry out a chi-square test of independence,the chi-square statistic is based on (rc-1)degrees of freedom where r and c denote,respectively the number of rows and columns n the contingency table.

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
12
In performing a chi-square goodness of fit test with multinomial probabilities,the smaller the difference between observed and expected frequencies,the higher the probability of concluding that the probabilities specified in the null hypothesis is correct.

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
13
The chi-square goodness of fit test can only be used to test whether a population has specified multinomial probabilities or to test if a sample has been selected from a normally distributed population.It cannot be applied to test if a sample data comes from other distribution forms such as Poisson.

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
14
A multinomial probability distribution describes data that is classified into two or more categories when a multinomial experiment is carried out.

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
15
A contingency table summarizes data that has been classified on two dimensions or scales.

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
16
In performing a chi-square test of independence,as the difference between the respective observed and expected frequencies decrease,the probability of concluding that the row variable is independent of the column variable decreases.

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
17
In a contingency table,if all of the expected frequencies equal the observed frequencies,then we can conclude that there is a perfect association between rows and columns.

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
18
Expected cell frequencies for a multinomial distribution are calculated by assuming statistical dependence.

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
19
A fastener manufacturing company uses a chi-square goodness of fit test to determine if a population of all lengths of ¼ inch bolts it manufactures is distributed according to a normal distribution.If we reject the null hypothesis,it is reasonable to assume that the population distribution is at least approximately normally distributed.

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
20
The chi-square distribution is a continuous probability distribution that is skewed to the left.

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
21
When we carry out a chi-square test of independence,the null hypothesis states that the two relevant classifications:
A)Are mutually exclusive
B)Form a contingency table with r rows and c columns
C)Have (r-1)(c-1)degrees of freedom
D)Are statistically dependent
E)Are normally distributed
A)Are mutually exclusive
B)Form a contingency table with r rows and c columns
C)Have (r-1)(c-1)degrees of freedom
D)Are statistically dependent
E)Are normally distributed

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
22
A manufacturing company produces part 2205 for the aerospace industry.This particular part can be manufactured using 3 different production processes.The management wants to know if the quality of the units of part 2205 is the same for all three processes.The production supervisor obtained the following data: Process 1 had 29 defective units in 240 items;Process 2 produced 12 defective units in 180 items and Process 3 manufactured 9 defective units in 150 items.At a significance level of .05,the management wants to perform a hypothesis test to determine whether the quality of items produced appears to be independent of the production process used.Calculate the expected number of defective units produced by Process 1.
A)29
B)21.053
C)218.947
D)6.042
E)10.786
A)29
B)21.053
C)218.947
D)6.042
E)10.786

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
23
A manufacturing company produces part 2205 for the aerospace industry.This particular part can be manufactured using 3 different production processes.The management wants to know if the quality of the units of part 2205 is the same for all three processes.The production supervisor obtained the following data: Process 1 had 29 defective units in 240 items;Process 2 produced 12 defective units in 180 items and Process 3 manufactured 9 defective units in 150 items.At a significance level of .05,the management wants to perform a hypothesis test to determine whether the quality of items produced appears to be independent of the production process used.What is the rejection point condition?
A)Reject H0 if 2 > .10257
B)Reject H0 if 2 > 9.3484
C)Reject H0 if 2 > 5.99147
D)Reject H0 if 2 > 7.37776
E)Reject H0 if 2 > 7.81473
A)Reject H0 if 2 > .10257
B)Reject H0 if 2 > 9.3484
C)Reject H0 if 2 > 5.99147
D)Reject H0 if 2 > 7.37776
E)Reject H0 if 2 > 7.81473

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
24
The chi-square goodness of fit test will be valid if each of the expected cell frequencies is ______________.
A)Greater than 0
B)Less than 5
C)Between 0 and 5
D)At least 1
E)At least 5
A)Greater than 0
B)Less than 5
C)Between 0 and 5
D)At least 1
E)At least 5

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
25
A manufacturing company produces part 2205 for the aerospace industry.This particular part can be manufactured using 3 different production processes.The management wants to know if the quality of the units of part 2205 is the same for all three processes.The production supervisor obtained the following data: Process 1 had 29 defective units in 240 items;Process 2 produced 12 defective units in 180 items and Process 3 manufactured 9 defective units in 150 items.At a significance level of .05 we performed chi-square test of independence to determine if the quality of the items produced appears to be independent of the production process.What are the degrees of freedom for the chi-square statistic?
A)2
B)3
C)520
D)569
E)570
A)2
B)3
C)520
D)569
E)570

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
26
When we carry out a chi-square test of independence,as the difference between the respective observed and expected frequencies decrease,the probability of concluding that the row variable is independent of the column variable:
A)Decreases
B)Increases
C)May decrease or increase depending on the number of rows and columns
D)Will be unaffected
A)Decreases
B)Increases
C)May decrease or increase depending on the number of rows and columns
D)Will be unaffected

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
27
Which if any of the following statements about the chi-square test of independence is false?
A)If ri is row total for row i and cj is the column total for column j,then the estimated expected cell frequency corresponding to row i and column j equals (ri)(cj)/n.
B)The test is valid if all of the estimated cell frequencies are at least five.
C)The chi-square statistic is based on (r-1)(c-1)degrees of freedom where r and c denote,respectively the number of rows and columns n the contingency table.
D)The alternative hypothesis states that the two classifications are statistically independent.
E)All of the above statements are true about the chi-square test of independence.
A)If ri is row total for row i and cj is the column total for column j,then the estimated expected cell frequency corresponding to row i and column j equals (ri)(cj)/n.
B)The test is valid if all of the estimated cell frequencies are at least five.
C)The chi-square statistic is based on (r-1)(c-1)degrees of freedom where r and c denote,respectively the number of rows and columns n the contingency table.
D)The alternative hypothesis states that the two classifications are statistically independent.
E)All of the above statements are true about the chi-square test of independence.

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
28
A manufacturing company produces part 2205 for the aerospace industry.This particular part can be manufactured using 3 different production processes.The management wants to know if the quality of the units of part 2205 is the same for all three processes.The production supervisor obtained the following data: Process 1 had 29 defective units in 240 items;Process 2 produced 12 defective units in 180 items and Process 3 manufactured 9 defective units in 150 items.At a significance level of .05,the management wants to perform a hypothesis test to determine whether the quality of items produced appears to be independent of the production process used.Calculate the expected number of conforming units produced by Process 2.
A)15.789
B)168
C)180
D)164.211
E)83.076
A)15.789
B)168
C)180
D)164.211
E)83.076

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
29
When we carry out a goodness of fit chi-square test,the expected frequencies are based on the alternative hypothesis.

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
30
A manufacturing company produces part 2205 for the aerospace industry.This particular part can be manufactured using 3 different production processes.The management wants to know if the quality of the units of part 2205 is the same for all three processes.The production supervisor obtained the following data: The Process 1 had 29 defective units in 240 items;Process 2 produced 12 defective units in 180 items and Process 3 manufactured 9 defective units in 150 items.At a significance level of .05,we performed a chi-square test to determine whether the quality of the items produced appear to be the same for all three processes.What is the null hypothesis?
A)H0: The number of defectives produced is independent of the production process used.
B)H0: The row and column variables are associated with each other.
C)H0: The proportion of defective units produced by the three production processes is the same.
D)Both A and C are correct or at least acceptable way of stating the null hypothesis.
E)A,B and C are all acceptable ways of stating the null hypothesis.
A)H0: The number of defectives produced is independent of the production process used.
B)H0: The row and column variables are associated with each other.
C)H0: The proportion of defective units produced by the three production processes is the same.
D)Both A and C are correct or at least acceptable way of stating the null hypothesis.
E)A,B and C are all acceptable ways of stating the null hypothesis.

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
31
When we carry out a chi-square goodness of fit test for a normal distribution,the null hypothesis states that the population:
A)Does not have a normal distribution
B)Has a normal distribution
C)Has a chi-square distribution
D)Does not have a chi-square distribution
E)Has k-3 degrees of freedom
A)Does not have a normal distribution
B)Has a normal distribution
C)Has a chi-square distribution
D)Does not have a chi-square distribution
E)Has k-3 degrees of freedom

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
32
A manufacturing company produces part 2205 for the aerospace industry.This particular part can be manufactured using 3 different production processes.The management wants to know if the quality of the units of part 2205 is the same for all three processes.The production supervisor obtained the following data: The Process 1 had 29 defective units in 240 items;Process 2 produced 12 defective units in 180 items and Process 3 manufactured 9 defective units in 150 items. 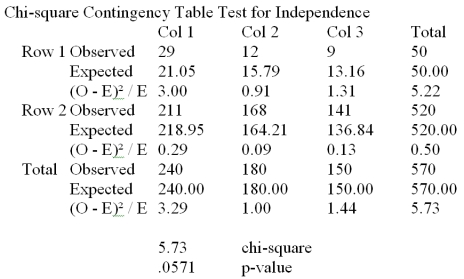 At a significance level of .10,the management wants to perform a hypothesis test to determine if the quality of the items produced appears to be independent of the production process used.Based on the results summarized in the Mega-Stat/Excel output provided in the table above,we:
At a significance level of .10,the management wants to perform a hypothesis test to determine if the quality of the items produced appears to be independent of the production process used.Based on the results summarized in the Mega-Stat/Excel output provided in the table above,we:
A)Reject H0 and conclude that the quality of the product is not the same for all processes.
B)Reject H0 and conclude that the quality of the product is dependent on the manufacturing process.
C)Failed to reject H0 and conclude that the quality of the product does not significantly differ among the three processes.
D)Reject H0 and conclude that the quality of the product is independent of the production process utilized.
E)Both A and B are correct.
 At a significance level of .10,the management wants to perform a hypothesis test to determine if the quality of the items produced appears to be independent of the production process used.Based on the results summarized in the Mega-Stat/Excel output provided in the table above,we:
At a significance level of .10,the management wants to perform a hypothesis test to determine if the quality of the items produced appears to be independent of the production process used.Based on the results summarized in the Mega-Stat/Excel output provided in the table above,we:A)Reject H0 and conclude that the quality of the product is not the same for all processes.
B)Reject H0 and conclude that the quality of the product is dependent on the manufacturing process.
C)Failed to reject H0 and conclude that the quality of the product does not significantly differ among the three processes.
D)Reject H0 and conclude that the quality of the product is independent of the production process utilized.
E)Both A and B are correct.

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
33
The chi-square goodness of fit test can be used when:
A)We conduct a binomial experiment.
B)We conduct a multinomial experiment.
C)We perform a hypothesis test to determine if a population has a normal distribution.
D)We perform a hypothesis test to determine if two population variances significantly differ from each other.
A)We conduct a binomial experiment.
B)We conduct a multinomial experiment.
C)We perform a hypothesis test to determine if a population has a normal distribution.
D)We perform a hypothesis test to determine if two population variances significantly differ from each other.

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
34
A manufacturing company produces part 2205 for the aerospace industry.This particular part can be manufactured using 3 different production processes.The management wants to know if the quality of the units of part 2205 is the same for all three processes.The production supervisor obtained the following data: The Process 1 had 29 defective units in 240 items;Process 2 produced 12 defective units in 180 items and Process 3 manufactured 9 defective units in 150 items. 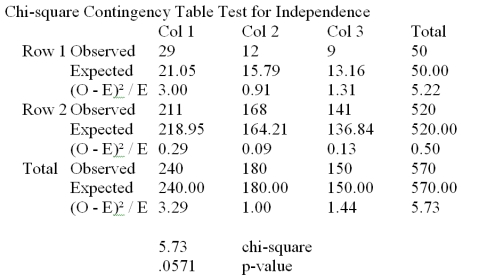 At a significance level of .05,the management wants to perform a hypothesis test to determine if the quality of the items produced appears to be independent of the production process used.Based on the results summarized in the Mega-Stat/Excel output provided in the table above,we:
At a significance level of .05,the management wants to perform a hypothesis test to determine if the quality of the items produced appears to be independent of the production process used.Based on the results summarized in the Mega-Stat/Excel output provided in the table above,we:
A)Reject H0 and conclude that the quality of the product is not the same for all processes.
B)Reject H0 and conclude that the quality of the product is dependent on the manufacturing process.
C)Failed to reject H0 and conclude that the quality of the product does not significantly differ among the three processes.
D)Failed to reject H0 and conclude that the quality of the product is not the same for all processes.
E)Reject H0 and conclude that the quality of the product is independent of the manufacturing process used.
 At a significance level of .05,the management wants to perform a hypothesis test to determine if the quality of the items produced appears to be independent of the production process used.Based on the results summarized in the Mega-Stat/Excel output provided in the table above,we:
At a significance level of .05,the management wants to perform a hypothesis test to determine if the quality of the items produced appears to be independent of the production process used.Based on the results summarized in the Mega-Stat/Excel output provided in the table above,we:A)Reject H0 and conclude that the quality of the product is not the same for all processes.
B)Reject H0 and conclude that the quality of the product is dependent on the manufacturing process.
C)Failed to reject H0 and conclude that the quality of the product does not significantly differ among the three processes.
D)Failed to reject H0 and conclude that the quality of the product is not the same for all processes.
E)Reject H0 and conclude that the quality of the product is independent of the manufacturing process used.

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
35
A real estate company is analyzing the selling prices of residential homes in a given community.140 homes that have been solved in the past month are randomly selected and their selling prices are recorded.The statistician working on the project has stated that in order to perform various statistical tests,the data must be distributed according to normal distribution.In order to determine whether the selling prices of homes included in the random sample are normally distributed,the data is divided into 6 classes of equal size and the number of observations in each class is recorded.The chi-square goodness of fit test for normal distribution is performed and the results are summarized in the following table: 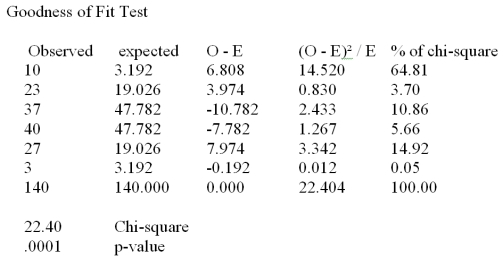 What are the degrees of freedom for the chi-square test?
What are the degrees of freedom for the chi-square test?
A)2
B)3
C)4
D)5
E)6
 What are the degrees of freedom for the chi-square test?
What are the degrees of freedom for the chi-square test?A)2
B)3
C)4
D)5
E)6

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
36
A real estate company is analyzing the selling prices of residential homes in a given community.140 homes that have been solved in the past month are randomly selected and their selling prices are recorded.The statistician working on the project has stated that in order to perform various statistical tests,the data must be distributed according to normal distribution.In order to determine whether the selling prices of homes included in the random sample are normally distributed,the data is divided into 6 classes of equal size and the number of observations in each class is recorded.The chi-square goodness of fit test for normal distribution is performed and the results are summarized in the following table: 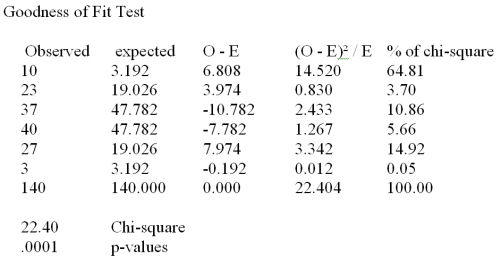 What is the appropriate null hypothesis?
What is the appropriate null hypothesis?
A)H0: The residential home selling prices are distributed according to normal distribution.
B)H0: The residential home selling prices are not distributed according to normal distribution.
C)H0: The distribution of residential home selling prices is either right or left skewed.
D)H0: The distribution of the residential home selling prices is symmetric.
E)None of the above is correct.
 What is the appropriate null hypothesis?
What is the appropriate null hypothesis?A)H0: The residential home selling prices are distributed according to normal distribution.
B)H0: The residential home selling prices are not distributed according to normal distribution.
C)H0: The distribution of residential home selling prices is either right or left skewed.
D)H0: The distribution of the residential home selling prices is symmetric.
E)None of the above is correct.

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
37
The 2 statistic from a contingency table with 6 rows and five columns will have
A)30 degrees of freedom
B)24 degrees of freedom
C)5 degrees of freedom
D)20 degrees of freedom
E)25 degrees of freedom
A)30 degrees of freedom
B)24 degrees of freedom
C)5 degrees of freedom
D)20 degrees of freedom
E)25 degrees of freedom

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
38
A real estate company is analyzing the selling prices of residential homes in a given community.140 homes that have been solved in the past month are randomly selected and their selling prices are recorded.The statistician working on the project has stated that in order to perform various statistical tests,the data must be distributed according to normal distribution.In order to determine whether the selling prices of homes included in the random sample are normally distributed,the data is divided into 6 classes of equal size and the number of observations in each class is recorded.The chi-square goodness of fit test for normal distribution is performed and the results are summarized in the following table: 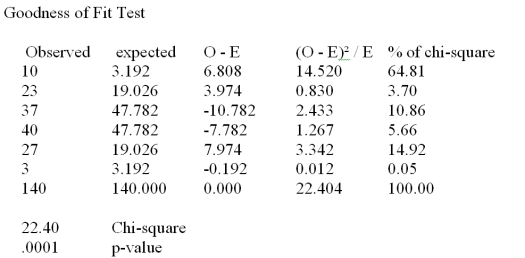
At a significance level of .05,what is the appropriate rejection point condition?
A)Reject H0 if 2 > 12.5916
B)Reject H0 if 2 > 11.0705
C)Reject H0 if 2 > 9.3484
D)Reject H0 if 2 > 7.81473
E)Reject H0 if 2 > 9.48773

At a significance level of .05,what is the appropriate rejection point condition?
A)Reject H0 if 2 > 12.5916
B)Reject H0 if 2 > 11.0705
C)Reject H0 if 2 > 9.3484
D)Reject H0 if 2 > 7.81473
E)Reject H0 if 2 > 9.48773

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
39
The chi-square goodness of fit is _________ a one-tailed test with the rejection region in the right tail.
A)Always
B)Sometimes
C)Never
A)Always
B)Sometimes
C)Never

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
40
The 2 statistic is used to test whether the assumption of normality is reasonable for a given population distribution.The sample consists of 5000 observations and is divided into 6 categories (intervals).The degrees of freedom for the chi-square statistic are:
A)4999
B)6
C)5
D)4
E)3
A)4999
B)6
C)5
D)4
E)3

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
41
Consider a set of 50 measurements with mean 50.2 and standard deviation 18.7 and with the following observed frequencies.  It is desired to test whether these measurements came from a normal population. Calculate the expected frequency for the interval 60-79.99.
It is desired to test whether these measurements came from a normal population. Calculate the expected frequency for the interval 60-79.99.
A)15.00
B)14.56
C)12.28
D)9.93
 It is desired to test whether these measurements came from a normal population. Calculate the expected frequency for the interval 60-79.99.
It is desired to test whether these measurements came from a normal population. Calculate the expected frequency for the interval 60-79.99.A)15.00
B)14.56
C)12.28
D)9.93

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
42
Consider a set of 50 measurements with mean 50.2 and standard deviation 18.7 and with the following observed frequencies.  It is desired to test whether these measurements came from a normal population. Calculate the expected frequency for the interval 40-59.99.
It is desired to test whether these measurements came from a normal population. Calculate the expected frequency for the interval 40-59.99.
A)20.37
B)18.00
C)14.56
D)12.50
 It is desired to test whether these measurements came from a normal population. Calculate the expected frequency for the interval 40-59.99.
It is desired to test whether these measurements came from a normal population. Calculate the expected frequency for the interval 40-59.99.A)20.37
B)18.00
C)14.56
D)12.50

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
43
Consider the 3X2 contingency table below.  At
At  = .05,determine the tabular value of the chi-square statistic used to test for the independence of Factors A and B?
= .05,determine the tabular value of the chi-square statistic used to test for the independence of Factors A and B?
A)12.6
B)11.1
C)7.81
D)5.99
 At
At  = .05,determine the tabular value of the chi-square statistic used to test for the independence of Factors A and B?
= .05,determine the tabular value of the chi-square statistic used to test for the independence of Factors A and B?A)12.6
B)11.1
C)7.81
D)5.99

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
44
In performing a chi-square test of independence,as the difference between respective observed and expected frequencies _________,the probability of concluding that the row variable is independent of the column variable increases.
A)stay the same
B)decrease
C)increase
D)double
A)stay the same
B)decrease
C)increase
D)double

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
45
An experiment consists of 400 observations,and four mutually exclusive groups.If the probability of a randomly selected item being classified into any of the four groups is equal,then the expected number of items that will be classified into group 1 is _____.
A)25
B)100
C)125
D)150
A)25
B)100
C)125
D)150

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
46
The number of degrees of freedom associated with a chi-square test for independence based upon a contingency table with 4 rows and 3 columns is _____.
A)7
B)12
C)5
D)6
A)7
B)12
C)5
D)6

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
47
In performing a chi-square goodness of fit test for a normal distribution,if there are 7 intervals,then the degrees of freedom for the chi-square statistic is ______________.
A)7
B)3
C)4
D)6
A)7
B)3
C)4
D)6

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
48
A special version of the chi-square goodness of fit test that involves testing the null hypothesis that all of the multinomial probabilities are equal is called the test for ___________.
A)goodness of fit
B)statistical independence
C)normality
D)homogeneity
A)goodness of fit
B)statistical independence
C)normality
D)homogeneity

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
49
A real estate company is analyzing the selling prices of residential homes in a given community.140 homes that have been solved in the past month are randomly selected and their selling prices are recorded.The statistician working on the project has stated that in order to perform various statistical tests,the data must be distributed according to normal distribution.In order to determine whether the selling prices of homes included in the random sample are normally distributed,the data is divided into 6 classes of equal size and the number of observations in each class is recorded.The chi-square goodness of fit test for normal distribution is performed and the results are summarized in the following table: 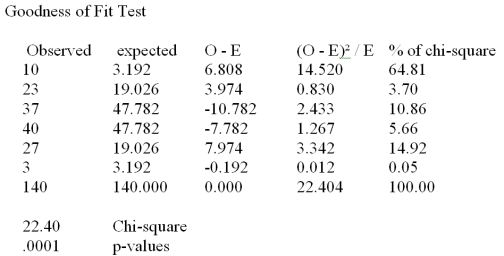 At a significance level of .05,we:
At a significance level of .05,we:
A)Reject H0 and conclude the residential home selling prices are not distributed according to normal distribution.
B)Failed to reject H0 and conclude the residential home selling prices are not distributed according to normal distribution.
C)Reject H0 and conclude the residential home selling prices are distributed according to normal distribution.
D)Failed to reject H0 and conclude the residential home selling prices are distributed according to normal distribution.
 At a significance level of .05,we:
At a significance level of .05,we:A)Reject H0 and conclude the residential home selling prices are not distributed according to normal distribution.
B)Failed to reject H0 and conclude the residential home selling prices are not distributed according to normal distribution.
C)Reject H0 and conclude the residential home selling prices are distributed according to normal distribution.
D)Failed to reject H0 and conclude the residential home selling prices are distributed according to normal distribution.

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
50
Consider a set of 50 measurements with mean 50.2 and standard deviation 18.7 and with the following observed frequencies.  It is desired to test whether these measurements came from a normal population. Calculate the expected frequency for the interval 0-39.99.
It is desired to test whether these measurements came from a normal population. Calculate the expected frequency for the interval 0-39.99.
A)10.44
B)12.00
C)14.56
D)12.50
 It is desired to test whether these measurements came from a normal population. Calculate the expected frequency for the interval 0-39.99.
It is desired to test whether these measurements came from a normal population. Calculate the expected frequency for the interval 0-39.99.A)10.44
B)12.00
C)14.56
D)12.50

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
51
Consider the 3X2 contingency table below.  At a significance level of .05,test H0: the factors A and B are independent.
At a significance level of .05,test H0: the factors A and B are independent.
A)Reject H0
B)Fail to reject H0
 At a significance level of .05,test H0: the factors A and B are independent.
At a significance level of .05,test H0: the factors A and B are independent.A)Reject H0
B)Fail to reject H0

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
52
Consider the 3X2 contingency table below.  How many degrees of freedom are associated with the chi-square test?
How many degrees of freedom are associated with the chi-square test?
A)6
B)5
C)2
D)3
 How many degrees of freedom are associated with the chi-square test?
How many degrees of freedom are associated with the chi-square test?A)6
B)5
C)2
D)3

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
53
Consider the 3X2 contingency table below.  Compute the expected frequencies in row 1.
Compute the expected frequencies in row 1.
A)16,14
B)20,30
C)12,18
D)15,15
 Compute the expected frequencies in row 1.
Compute the expected frequencies in row 1.A)16,14
B)20,30
C)12,18
D)15,15

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
54
In performing chi-square goodness fit test for a normal distribution,a researcher wants to make sure that all of the expected cell frequencies are at least five.The sample is divided into 7 intervals.The second through the sixth interval all have expected cell frequencies of at least five.The first and the last intervals have expected cell frequencies of 1.5 each.After adjusting the number of intervals,degrees of freedom for the chi-square statistic is ____.
A)2
B)3
C)5
D)7
A)2
B)3
C)5
D)7

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
55
The chi-square goodness of fit test for multinomial probabilities with 5 categories has _____ degrees of freedom.
A)5
B)4
C)3
D)6
A)5
B)4
C)3
D)6

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
56
In performing a chi-square goodness of fit test with multinomial probabilities,the ___________ the difference between observed and expected frequencies,the higher the probability of concluding that the probabilities specified in the null hypothesis is correct.
A)larger
B)smaller
A)larger
B)smaller

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
57
While a binomial distribution describes a count data that can be classified into one of two mutually exclusive categories,______________________ distribution describes count data that is classified into more than two mutually exclusive categories.
A)normal
B)skewed
C)uniform
D)multinomial
A)normal
B)skewed
C)uniform
D)multinomial

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
58
Consider the 3X2 contingency table below.  Compute the expected frequencies in row 3.
Compute the expected frequencies in row 3.
A)20,30
B)15,15
C)12,18
D)9,21
 Compute the expected frequencies in row 3.
Compute the expected frequencies in row 3.A)20,30
B)15,15
C)12,18
D)9,21

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
59
Consider the 3X2 contingency table below.  Compute the expected frequencies in row 2.
Compute the expected frequencies in row 2.
A)16,24
B)15,25
C)20,20
D)20,30
 Compute the expected frequencies in row 2.
Compute the expected frequencies in row 2.A)16,24
B)15,25
C)20,20
D)20,30

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
60
As the difference between observed frequency and expected frequency _______________,the probability of rejecting the null hypothesis increases.
A)stays the same
B)decreases
C)increases
D)go to 0
A)stays the same
B)decreases
C)increases
D)go to 0

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
61
In the past,of all the students enrolled in "Basic Business Statistics" 10% earned A's 20% earned B's,30% earned C's,20% earned D's and the rest either failed or withdrew from the course.Dr Johnson is a new professor teaching "Basic Business Statistics" for the first time this semester.At the conclusion of the semester,in Dr.Johnson's class of 60 students,there were 10 A's,20 B's,20 C's,5 D's and 5 W's or F's.Assume that Dr.Johnson's class constitutes a random sample.Dr Johnson wants to know if there is sufficient evidence to conclude that the grade distribution of his class is different than the historical grade distribution. Calculate the expected values for A's and D's.
A)10,5
B)10,12
C)12,12
D)12,5
A)10,5
B)10,12
C)12,12
D)12,5

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
62
A U.S.based internet company offers an on-line proficiency course in basic accounting.Completion of this online course satisfies the "Fundamentals of Accounting" course requirement in many MBA programs.In the first semester 315 students have enrolled in the course.The marketing research manager divided the country into seven regions of approximately equal populations.The course enrollment values in each of the seven regions are given below.The management wants to know if there is equal interest in the course across all regions. 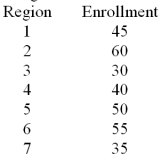 At a significance level of .01,test H0: the probabilities are equal for all seven regions.
At a significance level of .01,test H0: the probabilities are equal for all seven regions.
A)Reject H0
B)Fail to reject H0
 At a significance level of .01,test H0: the probabilities are equal for all seven regions.
At a significance level of .01,test H0: the probabilities are equal for all seven regions.A)Reject H0
B)Fail to reject H0

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
63
On the most recent tax cut proposal,a random sample of Democrats and Republicans in the Congress cast their votes as follows:  Determine the expected frequencies for both the Democrats and Republicans who favor the tax cut proposal for the chi-square test of independence.
Determine the expected frequencies for both the Democrats and Republicans who favor the tax cut proposal for the chi-square test of independence.
A)85,118
B)67.3,67.3
C)100.5,102.5
D)169.2,234.8
 Determine the expected frequencies for both the Democrats and Republicans who favor the tax cut proposal for the chi-square test of independence.
Determine the expected frequencies for both the Democrats and Republicans who favor the tax cut proposal for the chi-square test of independence.A)85,118
B)67.3,67.3
C)100.5,102.5
D)169.2,234.8

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
64
A U.S.based internet company offers an on-line proficiency course in basic accounting.Completion of this online course satisfies the "Fundamentals of Accounting" course requirement in many MBA programs.In the first semester 315 students have enrolled in the course.The marketing research manager divided the country into seven regions of approximately equal populations.The course enrollment values in each of the seven regions are given below.The management wants to know if there is equal interest in the course across all regions. 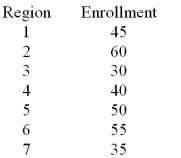 Calculate the expected enrollment (frequency)for all 7 regions.
Calculate the expected enrollment (frequency)for all 7 regions.
A)60
B)45
C)52.50
D)30
 Calculate the expected enrollment (frequency)for all 7 regions.
Calculate the expected enrollment (frequency)for all 7 regions.A)60
B)45
C)52.50
D)30

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
65
A U.S.based internet company offers an on-line proficiency course in basic accounting.Completion of this online course satisfies the "Fundamentals of Accounting" course requirement in many MBA programs.In the first semester 315 students have enrolled in the course.The marketing research manager divided the country into seven regions of approximately equal populations.The course enrollment values in each of the seven regions are given below.The management wants to know if there is equal interest in the course across all regions. 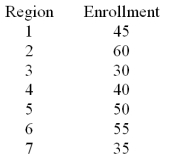 At a significance level of .05,test H0: the probabilities are equal for all seven regions.
At a significance level of .05,test H0: the probabilities are equal for all seven regions.
A)Reject H0
B)Fail to reject H0
 At a significance level of .05,test H0: the probabilities are equal for all seven regions.
At a significance level of .05,test H0: the probabilities are equal for all seven regions.A)Reject H0
B)Fail to reject H0

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
66
A U.S.based internet company offers an on-line proficiency course in basic accounting.Completion of this online course satisfies the "Fundamentals of Accounting" course requirement in many MBA programs.In the first semester 315 students have enrolled in the course.The marketing research manager divided the country into seven regions of approximately equal populations.The course enrollment values in each of the seven regions are given below.The management wants to know if there is equal interest in the course across all regions. 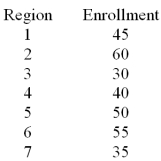 How many degrees of freedom are associated with the chi-square test and at
How many degrees of freedom are associated with the chi-square test and at 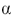 = .05 determine the rejection point condition of the chi-square statistic.
= .05 determine the rejection point condition of the chi-square statistic.
A)7,14.1
B)6,12.6
C)6,16.8
D)7,12.0
 How many degrees of freedom are associated with the chi-square test and at
How many degrees of freedom are associated with the chi-square test and at 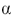 = .05 determine the rejection point condition of the chi-square statistic.
= .05 determine the rejection point condition of the chi-square statistic.A)7,14.1
B)6,12.6
C)6,16.8
D)7,12.0

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
67
In the past,of all the students enrolled in "Basic Business Statistics" 10% earned A's 20% earned B's,30% earned C's,20% earned D's and the rest either failed or withdrew from the course.Dr Johnson is a new professor teaching "Basic Business Statistics" for the first time this semester.At the conclusion of the semester,in Dr.Johnson's class of 60 students,there were 10 A's,20 B's,20 C's,5 D's and 5 W's or F's.Assume that Dr.Johnson's class constitutes a random sample.Dr Johnson wants to know if there is sufficient evidence to conclude that the grade distribution of his class is different than the historical grade distribution. Use 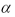 = .05,and determine the appropriate degrees of freedom and the rejection point condition associated with this goodness of fit test.
= .05,and determine the appropriate degrees of freedom and the rejection point condition associated with this goodness of fit test.
A)5,11.1
B)4,11.1
C)4,9.5
D)5,9.5
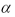 = .05,and determine the appropriate degrees of freedom and the rejection point condition associated with this goodness of fit test.
= .05,and determine the appropriate degrees of freedom and the rejection point condition associated with this goodness of fit test.A)5,11.1
B)4,11.1
C)4,9.5
D)5,9.5

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
68
A U.S.based internet company offers an on-line proficiency course in basic accounting.Completion of this online course satisfies the "Fundamentals of Accounting" course requirement in many MBA programs.In the first semester 315 students have enrolled in the course.The marketing research manager divided the country into seven regions of approximately equal populations.The course enrollment values in each of the seven regions are given below.The management wants to know if there is equal interest in the course across all regions. 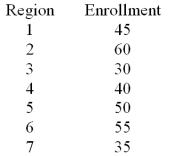 Calculate the value of the chi-square statistic.
Calculate the value of the chi-square statistic.
A)0
B)2.22
C)15.56
D)2.89
 Calculate the value of the chi-square statistic.
Calculate the value of the chi-square statistic.A)0
B)2.22
C)15.56
D)2.89

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
69
On the most recent tax cut proposal,a random sample of Democrats and Republicans in the Congress cast their votes as follows:  Determine the expected frequencies for both the Democrats and Republicans who oppose the tax cut proposal for the chi-square test of independence.
Determine the expected frequencies for both the Democrats and Republicans who oppose the tax cut proposal for the chi-square test of independence.
A)68.8,70.2
B)67.3,67.3
C)78,61
D)69.5,69.5
 Determine the expected frequencies for both the Democrats and Republicans who oppose the tax cut proposal for the chi-square test of independence.
Determine the expected frequencies for both the Democrats and Republicans who oppose the tax cut proposal for the chi-square test of independence.A)68.8,70.2
B)67.3,67.3
C)78,61
D)69.5,69.5

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
70
In the past,of all the students enrolled in "Basic Business Statistics" 10% earned A's 20% earned B's,30% earned C's,20% earned D's and the rest either failed or withdrew from the course.Dr Johnson is a new professor teaching "Basic Business Statistics" for the first time this semester.At the conclusion of the semester,in Dr.Johnson's class of 60 students,there were 10 A's,20 B's,20 C's,5 D's and 5 W's or F's.Assume that Dr.Johnson's class constitutes a random sample.Dr Johnson wants to know if there is sufficient evidence to conclude that the grade distribution of his class is different than the historical grade distribution. Calculate the expected values for B's and C's.
A)20,20
B)12,12
C)12,18
D)20,18
A)20,20
B)12,12
C)12,18
D)20,18

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
71
In the past,of all the students enrolled in "Basic Business Statistics" 10% earned A's 20% earned B's,30% earned C's,20% earned D's and the rest either failed or withdrew from the course.Dr Johnson is a new professor teaching "Basic Business Statistics" for the first time this semester.At the conclusion of the semester,in Dr.Johnson's class of 60 students,there were 10 A's,20 B's,20 C's,5 D's and 5 W's or F's.Assume that Dr.Johnson's class constitutes a random sample.Dr Johnson wants to know if there is sufficient evidence to conclude that the grade distribution of his class is different than the historical grade distribution. At = .05,test to determine if the grade distribution for Dr.Johnson's class is different than the historical grade distribution.
A)Reject H0
B)Fail to reject H0
A)Reject H0
B)Fail to reject H0

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
72
Consider a set of 50 measurements with mean 50.2 and standard deviation 18.7 and with the following observed frequencies.  It is desired to test whether these measurements came from a normal population. Calculate the expected frequency for the interval 80 and higher.
It is desired to test whether these measurements came from a normal population. Calculate the expected frequency for the interval 80 and higher.
A)5.00
B)12.50
C)2.80
D)22.21
 It is desired to test whether these measurements came from a normal population. Calculate the expected frequency for the interval 80 and higher.
It is desired to test whether these measurements came from a normal population. Calculate the expected frequency for the interval 80 and higher.A)5.00
B)12.50
C)2.80
D)22.21

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
73
At a significance level of .01,determine the appropriate degrees of freedom and the rejection point condition for this test.
A)5,15.1
B)1,6.63
C)6,16.8
D)2,9.21
A)5,15.1
B)1,6.63
C)6,16.8
D)2,9.21

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
74
Consider a set of 50 measurements with mean 50.2 and standard deviation 18.7 and with the following observed and expected frequencies.  It is desired to test whether these measurements came from a normal population.At a significance level of .05,test H0: the set of 50 measurements came from a normal population.
It is desired to test whether these measurements came from a normal population.At a significance level of .05,test H0: the set of 50 measurements came from a normal population.
A)Reject H0
B)Fail to reject H0
 It is desired to test whether these measurements came from a normal population.At a significance level of .05,test H0: the set of 50 measurements came from a normal population.
It is desired to test whether these measurements came from a normal population.At a significance level of .05,test H0: the set of 50 measurements came from a normal population.A)Reject H0
B)Fail to reject H0

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
75
Consider a set of 50 measurements with mean 50.2 and standard deviation 18.7 and with the following observed and expected frequencies.  It is desired to test whether these measurements came from a normal population.Calculate the value of the chi-square test statistic?
It is desired to test whether these measurements came from a normal population.Calculate the value of the chi-square test statistic?
A)2.32
B)3.07
C)1.30
D)0.72
 It is desired to test whether these measurements came from a normal population.Calculate the value of the chi-square test statistic?
It is desired to test whether these measurements came from a normal population.Calculate the value of the chi-square test statistic?A)2.32
B)3.07
C)1.30
D)0.72

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
76
A U.S.based internet company offers an on-line proficiency course in basic accounting.Completion of this online course satisfies the "Fundamentals of Accounting" course requirement in many MBA programs.In the first semester 315 students have enrolled in the course.The marketing research manager divided the country into seven regions of approximately equal populations.The course enrollment values in each of the seven regions are given below.The management wants to know if there is equal interest in the course across all regions. 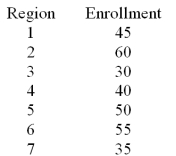 Assume that H0 - equal probabilities across regions is rejected.State a one sentence managerial conclusion.
Assume that H0 - equal probabilities across regions is rejected.State a one sentence managerial conclusion.
A)It appears that the enrollment differs among all of the seven regions.
B)It appears that the enrollments across the seven regions are equal.
C)It appears that the enrollment differs among some of the seven regions.
D)We cannot draw conclusions about enrollment differences among the seven regions.
 Assume that H0 - equal probabilities across regions is rejected.State a one sentence managerial conclusion.
Assume that H0 - equal probabilities across regions is rejected.State a one sentence managerial conclusion.A)It appears that the enrollment differs among all of the seven regions.
B)It appears that the enrollments across the seven regions are equal.
C)It appears that the enrollment differs among some of the seven regions.
D)We cannot draw conclusions about enrollment differences among the seven regions.

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
77
A U.S.based internet company offers an on-line proficiency course in basic accounting.Completion of this online course satisfies the "Fundamentals of Accounting" course requirement in many MBA programs.In the first semester 315 students have enrolled in the course.The marketing research manager divided the country into seven regions of approximately equal populations.The course enrollment values in each of the seven regions are given below.The management wants to know if there is equal interest in the course across all regions. 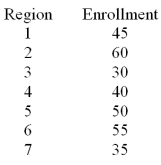 Assume that H0: p1 = p2 = p3 = p4 = p5 = p6 = p7 is not rejected and state a one sentence managerial conclusion.
Assume that H0: p1 = p2 = p3 = p4 = p5 = p6 = p7 is not rejected and state a one sentence managerial conclusion.
A)It appears that the enrollment differs among all of the seven regions.
B)It appears that the enrollments across the seven regions are equal.
C)It appears that the enrollment differs among some of the seven regions.
D)We cannot draw conclusions about enrollment differences among the seven regions.
 Assume that H0: p1 = p2 = p3 = p4 = p5 = p6 = p7 is not rejected and state a one sentence managerial conclusion.
Assume that H0: p1 = p2 = p3 = p4 = p5 = p6 = p7 is not rejected and state a one sentence managerial conclusion.A)It appears that the enrollment differs among all of the seven regions.
B)It appears that the enrollments across the seven regions are equal.
C)It appears that the enrollment differs among some of the seven regions.
D)We cannot draw conclusions about enrollment differences among the seven regions.

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
78
In the past,of all the students enrolled in "Basic Business Statistics" 10% earned A's 20% earned B's,30% earned C's,20% earned D's and the rest either failed or withdrew from the course.Dr Johnson is a new professor teaching "Basic Business Statistics" for the first time this semester.At the conclusion of the semester,in Dr.Johnson's class of 60 students,there were 10 A's,20 B's,20 C's,5 D's and 5 W's or F's.Assume that Dr.Johnson's class constitutes a random sample.Dr Johnson wants to know if there is sufficient evidence to conclude that the grade distribution of his class is different than the historical grade distribution. If we assume at  = .05 that the null hypothesis is rejected,make a one-sentence managerial conclusion.
= .05 that the null hypothesis is rejected,make a one-sentence managerial conclusion.
A)Dr.Johnson's class grades don't differ from the historical course grade distribution.
B)Dr.Johnson's class grades are higher than the historical course grade distribution.
C)Dr.Johnson's class grades are Lower than the historical course grade distribution.
D)We cannot draw a conclusion about the difference between Dr.Johnson's grades and the historical course grade distribution.
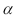 = .05 that the null hypothesis is rejected,make a one-sentence managerial conclusion.
= .05 that the null hypothesis is rejected,make a one-sentence managerial conclusion.A)Dr.Johnson's class grades don't differ from the historical course grade distribution.
B)Dr.Johnson's class grades are higher than the historical course grade distribution.
C)Dr.Johnson's class grades are Lower than the historical course grade distribution.
D)We cannot draw a conclusion about the difference between Dr.Johnson's grades and the historical course grade distribution.

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
79
Consider a set of 50 measurements with mean 50.2 and standard deviation 18.7 and with the following observed frequencies.  It is desired to test whether these measurements came from a normal population. How many degrees of freedom are associated with the chi-square test?
It is desired to test whether these measurements came from a normal population. How many degrees of freedom are associated with the chi-square test?
A)1
B)4
C)3
D)2
 It is desired to test whether these measurements came from a normal population. How many degrees of freedom are associated with the chi-square test?
It is desired to test whether these measurements came from a normal population. How many degrees of freedom are associated with the chi-square test?A)1
B)4
C)3
D)2

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck
80
In the past,of all the students enrolled in "Basic Business Statistics" 10% earned A's 20% earned B's,30% earned C's,20% earned D's and the rest either failed or withdrew from the course.Dr Johnson is a new professor teaching "Basic Business Statistics" for the first time this semester.At the conclusion of the semester,in Dr.Johnson's class of 60 students,there were 10 A's,20 B's,20 C's,5 D's and 5 W's or F's.Assume that Dr.Johnson's class constitutes a random sample.Dr Johnson wants to know if there is sufficient evidence to conclude that the grade distribution of his class is different than the historical grade distribution. Calculate the chi-square statistic.
A)9.5
B)3.03
C)2.33
D)16.4
A)9.5
B)3.03
C)2.33
D)16.4

Unlock Deck
Unlock for access to all 96 flashcards in this deck.
Unlock Deck
k this deck


