Deck 15: Applications of the Schrodinger Equation
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/54
Play
Full screen (f)
Deck 15: Applications of the Schrodinger Equation
1
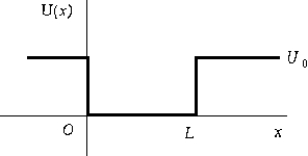 For the finite square well shown in the figure,
For the finite square well shown in the figure,A) U(x) = U0, x < 0
B) U(x) = 0, 0 < x < L
C) U(x) = U0, x > 0
D) U, although discontinuous, is finite everywhere.
E) All of these are correct.
All of these are correct.
2
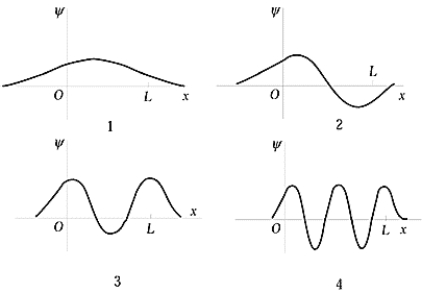 The graph that shows the third state for a particle in a finite square well is
The graph that shows the third state for a particle in a finite square well isA) 1
B) 2
C) 3
D) 4
E) None of these is correct.
3
3
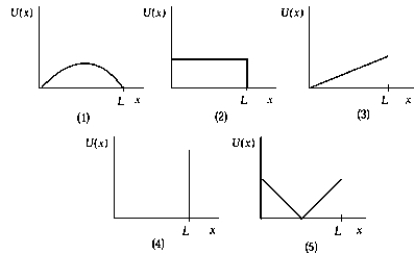 The graph that represents the potential energy for a one-dimensional box from x = 0 to x = L is
The graph that represents the potential energy for a one-dimensional box from x = 0 to x = L isA) 1
B) 2
C) 3
D) 4
E) 5
4
4
The solution for the time-independent Schrödinger equation with the following potential function and boundary conditions
U(x) = 0, -L/2 x L/2
U(x) = , x < -L/2 or x > L/2
Is
A)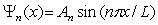 , where
, where 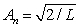 and n = 1, 2, 3, ..
and n = 1, 2, 3, ..
B)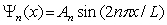 , where
, where 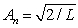 and n = 1, 2, 3, ..
and n = 1, 2, 3, ..
C)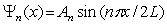 , where
, where 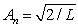 and n = 1, 2, 3, ..
and n = 1, 2, 3, ..
D)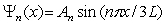 , where
, where 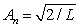 and n = 1, 2, 3, ..
and n = 1, 2, 3, ..
E) There is no solution for the given potential function and boundary conditions.
U(x) = 0, -L/2 x L/2
U(x) = , x < -L/2 or x > L/2
Is
A)
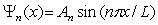 , where
, where 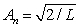 and n = 1, 2, 3, ..
and n = 1, 2, 3, ..B)
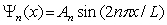 , where
, where 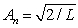 and n = 1, 2, 3, ..
and n = 1, 2, 3, ..C)
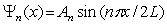 , where
, where 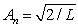 and n = 1, 2, 3, ..
and n = 1, 2, 3, ..D)
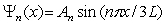 , where
, where 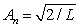 and n = 1, 2, 3, ..
and n = 1, 2, 3, ..E) There is no solution for the given potential function and boundary conditions.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
5
Suppose the natural frequency of oscillation for H2 is 1012 Hz, the effective spring constant between the two H atoms is of the order
A) 10-1 N/m
B) 10-3 N/m
C) 10-5 N/m
D) 10-7 N/m
E) 10-9 N/m
A) 10-1 N/m
B) 10-3 N/m
C) 10-5 N/m
D) 10-7 N/m
E) 10-9 N/m

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
6
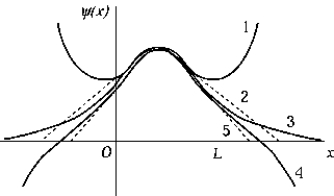 The curve that best represents the ground-state energy for a finite square well is
The curve that best represents the ground-state energy for a finite square well isA) 1
B) 2
C) 3
D) 4
E) 5

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
7
The energy in the first excited state of an electron confined to a one-dimensional box of length L = 0.2 nm is
A) 9.40 eV
B) 12.3 eV
C) 19.7 eV
D) 24.2 eV
E) 37.6 eV
A) 9.40 eV
B) 12.3 eV
C) 19.7 eV
D) 24.2 eV
E) 37.6 eV

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
8
The energy in the ground state of an electron confined to a one-dimensional box of length L = 0.3 nm is
A) 2.47 eV
B) 4.18 eV
C) 6.25 eV
D) 9.40 eV
E) None of these is correct.
A) 2.47 eV
B) 4.18 eV
C) 6.25 eV
D) 9.40 eV
E) None of these is correct.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
9
The energy in the ground state of an electron confined to a one-dimensional box of length L = 0.2 nm is
A) 1.88 eV
B) 4.47 eV
C) 6.25 eV
D) 9.40 eV
E) None of these is correct.
A) 1.88 eV
B) 4.47 eV
C) 6.25 eV
D) 9.40 eV
E) None of these is correct.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
10
Match each of the wave function on the left for a particle in a finite square well with the corresponding probability distributions on the right, in the order (a), (b), and (c).
(a)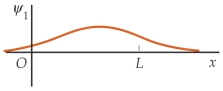 (I)
(I) 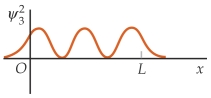 (b)
(b) 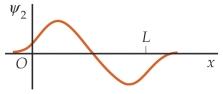 (II)
(II) 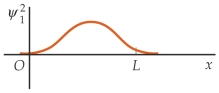 (c)
(c) 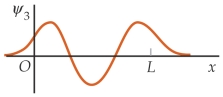 (III)
(III) 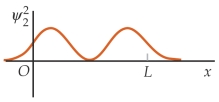
A) (II) (I) (III)
B) (II) (III) (I)
C) (III) (I) (II)
D) (III) (II) (I)
E) (I) (III) (II)
(a)
 (I)
(I)  (b)
(b)  (II)
(II)  (c)
(c)  (III)
(III) 
A) (II) (I) (III)
B) (II) (III) (I)
C) (III) (I) (II)
D) (III) (II) (I)
E) (I) (III) (II)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
11
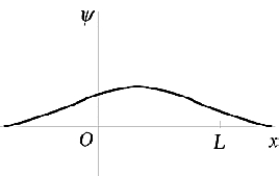 The penetration of the wave function beyond the edges of the finite square-well potential shown in the figure
The penetration of the wave function beyond the edges of the finite square-well potential shown in the figureA) indicates that there is some small probability of finding the particle outside the well.
B) forces us to conclude that E - U0 is negative in these regions.
C) suggests that these regions are classically forbidden.
D) is unexplainable classically.
E) is described by all of the above.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
12
An electron confined to a one-dimensional box of length L = 0.2 nm makes a transition from state n = 4 to state n = 3. The wavelength of the photon emitted is
A) 19.0 nm
B) 17.2 nm
C) 14.6 nm
D) 12.5 nm
E) 10.8 nm
A) 19.0 nm
B) 17.2 nm
C) 14.6 nm
D) 12.5 nm
E) 10.8 nm

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
13
The energy in the first excited state of an electron confined to a one-dimensional box of length L = 0.3 nm is
A) 9.40 eV
B) 12.3 eV
C) 16.7 eV
D) 24.2 eV
E) 37.6 eV
A) 9.40 eV
B) 12.3 eV
C) 16.7 eV
D) 24.2 eV
E) 37.6 eV

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
14
The dependent variable in the Schrödinger equation is
A) the wave function .
B) the position variable x.
C) the time variable t.
D) the potential energy function U.
E) None of these is correct.
A) the wave function .
B) the position variable x.
C) the time variable t.
D) the potential energy function U.
E) None of these is correct.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
15
The wave function for a particle in a one-dimensional box of length L
A) is constrained by the boundary conditions (0) = 0 and (L) = 0.
B) must be zero everywhere outside of the box.
C) is given by (x) = A sin kx, where A is a constant.
D) restricts the possible energy of the particle to E =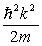 .
.
E) All of these are correct.
A) is constrained by the boundary conditions (0) = 0 and (L) = 0.
B) must be zero everywhere outside of the box.
C) is given by (x) = A sin kx, where A is a constant.
D) restricts the possible energy of the particle to E =
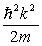 .
.E) All of these are correct.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
16
An electron confined to a one-dimensional box of length L = 0.3 nm makes a transition from state n = 4 to state n = 2. The wavelength of the photon emitted is
A) 19.0 nm
B) 24.7 nm
C) 28.9 nm
D) 33.6 nm
E) 41.2 nm
A) 19.0 nm
B) 24.7 nm
C) 28.9 nm
D) 33.6 nm
E) 41.2 nm

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
17
The Schrödinger equation
A) is a partial differential equation in space and time.
B) (like Newton's laws of motion) cannot be derived.
C) depends upon experimentation for its verification.
D) relates the second space-derivative of the wave function to the first time-derivative of the wave function.
E) All of these are correct.
A) is a partial differential equation in space and time.
B) (like Newton's laws of motion) cannot be derived.
C) depends upon experimentation for its verification.
D) relates the second space-derivative of the wave function to the first time-derivative of the wave function.
E) All of these are correct.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
18
In order to solve the Schrödinger's equation, which of the following quantity(ies) must be specified?
A) the kinetic energy function of the particle
B) the potential energy function of the particle
C) the boundary conditions
D) (A) and (B)
E) (B) and (C)
A) the kinetic energy function of the particle
B) the potential energy function of the particle
C) the boundary conditions
D) (A) and (B)
E) (B) and (C)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
19
The time-independent Schrödinger equation is
A)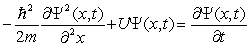
B)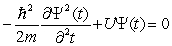
C)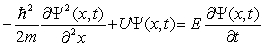
D)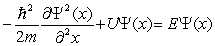
E)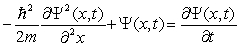
A)
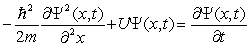
B)
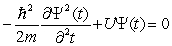
C)
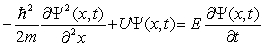
D)
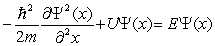
E)
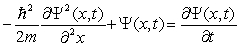

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
20
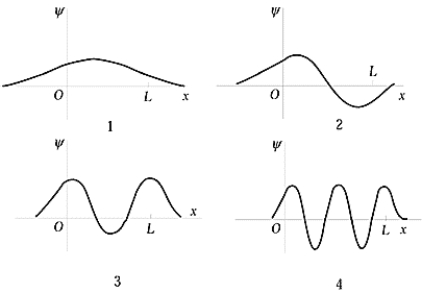 The graph that shows the second state for a particle in a finite square well is
The graph that shows the second state for a particle in a finite square well isA) 1
B) 2
C) 3
D) 4
E) None of these is correct.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
21
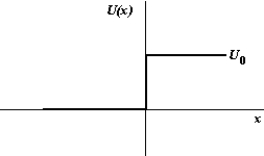 When a particle of energy E encounters the step function shown in the figure,
When a particle of energy E encounters the step function shown in the figure,A) the classical and quantum-mechanical descriptions are in agreement provided
E < U0.
B) the wave function does not go to zero at x = 0 but rather decays exponentially.
C) the particle will sometimes be transmitted and sometimes reflected if E > U0.
D) the wavelength of the particle changes abruptly at x = 0 if E > U0.
E) All of these are true.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
22
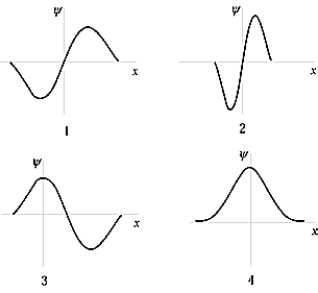 The ground-state wave function of the harmonic oscillator is best represented by
The ground-state wave function of the harmonic oscillator is best represented byA) 1
B) 2
C) 3
D) 4
E) None of these is correct.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
23
The ground-state wave function of the harmonic oscillator is
A)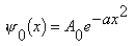
B) 0(x) = A0e-ax
C) 0(x) = A0sin(ax)
D) 0(x) = A0sin(ax2)
E)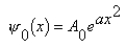
A)
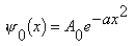
B) 0(x) = A0e-ax
C) 0(x) = A0sin(ax)
D) 0(x) = A0sin(ax2)
E)
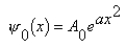

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
24
A proton of energy E0 traveling in a region in which the potential energy is zero is incident on a potential barrier of height U0 = 0.5E0. The probability that the proton will be transmitted is
A) 85.3%
B) 89.2%
C) 92.4%
D) 97.1%
E) 98.3%
A) 85.3%
B) 89.2%
C) 92.4%
D) 97.1%
E) 98.3%

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
25
A particle of energy E0 traveling in a region in which the potential energy is zero is incident on a potential barrier of height U0 = 0.3E0. The probability that the particle will be reflected is
A) 0.316%
B) 0.791%
C) 2.89%
D) 3.56%
E) 4.12%
A) 0.316%
B) 0.791%
C) 2.89%
D) 3.56%
E) 4.12%

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
26
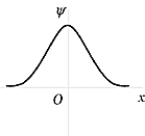 The wave function shown in the figure represents the n = _______ energy state of the harmonic oscillator.
The wave function shown in the figure represents the n = _______ energy state of the harmonic oscillator.A) 0
B) 1
C) 2
D) 3
E) 4

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
27
The probability of penetration of a rectangular barrier __________ with the square root of the relative barrier height.
A) increases linearly
B) decreases exponentially
C) decreases linearly
D) increases exponentially
E) decreases as a damped sinusoid
A) increases linearly
B) decreases exponentially
C) decreases linearly
D) increases exponentially
E) decreases as a damped sinusoid

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
28
The probability of penetration of a rectangular barrier decreases exponentially with the ________ of the barrier height.
A) square
B) cube
C) square root
D) cube root
E) fourth root
A) square
B) cube
C) square root
D) cube root
E) fourth root

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
29
Suppose the natural frequency of oscillation for H2 is 1012 Hz and the amplitude of oscillation is 10-12 m, the total energy of the harmonic oscillator is of the order
A) 10-20 J
B) 10-22 J
C) 10-24 J
D) 10-26 J
E) 10-28 J
A) 10-20 J
B) 10-22 J
C) 10-24 J
D) 10-26 J
E) 10-28 J

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
30
The probability of penetration of a rectangular barrier ________ with the barrier thickness.
A) increases linearly
B) decreases exponentially
C) decreases linearly
D) increases exponentially
E) decreases as a damped sinusoid
A) increases linearly
B) decreases exponentially
C) decreases linearly
D) increases exponentially
E) decreases as a damped sinusoid

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
31
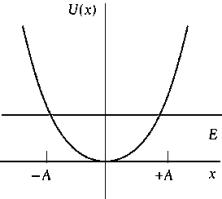 The potential energy function shown in the above figure
The potential energy function shown in the above figureA) applies to any system undergoing small oscillations about a position of stable equilibrium.
B) shows the classical turning points ±A.
C) tells that where -A < x < +A, the total energy is greater than the potential energy.
D) indicates that U(x) is directly proportional to x2.
E) All of these are correct.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
32
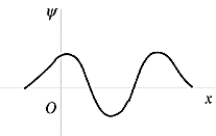 The wave function shown in the figure represents the n = _______ energy state of the harmonic oscillator.
The wave function shown in the figure represents the n = _______ energy state of the harmonic oscillator.A) 0
B) 1
C) 2
D) 3
E) 4

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
33
Which of the following statements is true?
A) A particle that is confined to some region of space can have zero energy.
B) All phenomena in nature are adequately described by classical wave theory.
C) The Schrödinger equation can be derived from Newton's laws of motion.
D) The penetration of a barrier by a wave has physical significance.
E) None of these is true.
A) A particle that is confined to some region of space can have zero energy.
B) All phenomena in nature are adequately described by classical wave theory.
C) The Schrödinger equation can be derived from Newton's laws of motion.
D) The penetration of a barrier by a wave has physical significance.
E) None of these is true.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
34
The quantum phenomenon known as the "tunnel effect" refers to
A) highly eccentric electron orbits penetrating inner closed shells.
B) the fine structure exhibited by many spectral lines.
C) the small but finite probability that an -particle originally within the nucleus will be found outside the nucleus.
D) the penetration of shielding by high-energy fission neutrons.
E) an orbital electron penetrating the nucleus and undergoing electron capture.
A) highly eccentric electron orbits penetrating inner closed shells.
B) the fine structure exhibited by many spectral lines.
C) the small but finite probability that an -particle originally within the nucleus will be found outside the nucleus.
D) the penetration of shielding by high-energy fission neutrons.
E) an orbital electron penetrating the nucleus and undergoing electron capture.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
35
A particle of kinetic energy E0 traveling in a region in which the potential energy is zero is then incident on a potential barrier of height U0. What is the ratio of E0/U0 so that the reflection co-efficient is 75%? (Assume E0 is much less than the rest mass energy of the particle.)
A) 1.250
B) 0.7500
C) 1.778
D) 1.005
E) 1.063
A) 1.250
B) 0.7500
C) 1.778
D) 1.005
E) 1.063

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
36
A particle of kinetic energy E0 traveling in a region in which the potential energy is zero is then incident on a potential barrier of height U0. What is the ratio of E0/U0 so that the reflection co-efficient is 25%? (Assume E0 is much less than the rest mass energy of the particle.)
A) 4.0
B) 1.25
C) 1.125
D) 1.025
E) 0.75
A) 4.0
B) 1.25
C) 1.125
D) 1.025
E) 0.75

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
37
An electron of energy E0 traveling in a region in which the potential energy is zero is incident on a potential barrier of height U0 = 0.5E0. The ratio of the wavelength of the transmitted wave to the incident wave is
A) 2
B) 1
C) 0.5
D)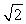
E)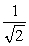
A) 2
B) 1
C) 0.5
D)
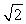
E)
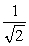

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
38
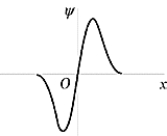 The wave function shown in the figure represents the n = _______ energy state of the harmonic oscillator.
The wave function shown in the figure represents the n = _______ energy state of the harmonic oscillator.A) 0
B) 1
C) 2
D) 3
E) 4

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
39
A particle of energy E0 traveling in a region in which the potential energy is zero is incident on a potential barrier of height U0 = 0.4E0. The probability that the particle will be reflected is
A) 0.316%
B) 0.789%
C) 1.61%
D) 3.56%
E) 4.12%
A) 0.316%
B) 0.789%
C) 1.61%
D) 3.56%
E) 4.12%

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
40
An electron with kinetic energy 5.0 eV traveling in a region in which the potential energy is zero is incident at x > 0 on a potential barrier of height 3.0 eV. What is the wavelength of the electron in the region x > 0?
A) 0.87 nm
B) 0.99 nm
C) 0.54 nm
D) 2.3 nm
E) 0.14 nm
A) 0.87 nm
B) 0.99 nm
C) 0.54 nm
D) 2.3 nm
E) 0.14 nm

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
41
An electron is confined in a two-dimensional box where U(x,y) = 0 for x = 0 to L, and y = 0 to 3L, and U(x,y) = infinity outside these boundaries. If L = 0.5 nm then calculate the energy of the first doubly degenerate levels.
A) 9.9 eV
B) 11.0 eV
C) 8.5 eV
D) 7.7 eV
E) 6.2 eV
A) 9.9 eV
B) 11.0 eV
C) 8.5 eV
D) 7.7 eV
E) 6.2 eV

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
42
A particle is in a three-dimensional box with L3 = L2 = 3L1. The lowest energy level is
A) zero
B) 1.22E0
C) 1.56E0
D) 1.67E0
E) 1.94E0
A) zero
B) 1.22E0
C) 1.56E0
D) 1.67E0
E) 1.94E0

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
43
An electron is confined in a two-dimensional box where U(x,y) = 0 for x = 0 to L and y = 0 to 3L, and U(x,y) = infinity outside these boundaries. If L = 0.5 nm, then calculate the energy of the first excited state.
A) 1.7 eV
B) 2.2 eV
C) 6.2 eV
D) 3.0 eV
E) None of these is correct.
A) 1.7 eV
B) 2.2 eV
C) 6.2 eV
D) 3.0 eV
E) None of these is correct.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
44
Particles that have antisymmetric wave functions and are described by the Pauli exclusion principle are called
A) quarks
B) leptons
C) fermions
D) bosons
E) None of these is correct.
A) quarks
B) leptons
C) fermions
D) bosons
E) None of these is correct.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
45
A particle is confined in a three-dimensional box with L1 = L2 = 3L3. The quantum numbers for the second excited state are
A) (1,1,2) and (1,2,1)
B) (1,2,1) and (2,1,1)
C) (2,2,1) and (2,1,2)
D) (1,2,2) and (2,1,2)
E) (2,2,1) and (1,2,2)
A) (1,1,2) and (1,2,1)
B) (1,2,1) and (2,1,1)
C) (2,2,1) and (2,1,2)
D) (1,2,2) and (2,1,2)
E) (2,2,1) and (1,2,2)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
46
A particle is in a three-dimensional box with L3 = L2 = 3L1. The energy level E1,1,2 is
A) zero
B) 1.22E0
C) 1.56E0
D) 1.67E0
E) 1.94E0
A) zero
B) 1.22E0
C) 1.56E0
D) 1.67E0
E) 1.94E0

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
47
An electron of kinetic energy E0 traveling in a region in which the potential energy is zero is then incident on a finite potential barrier of height U0 (= 4E0) and width a. If the potential barrier is reduced to 2E0, by what factor will the probability of penetration of the barrier be changed?
A)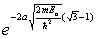
B)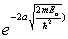
C)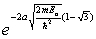
D)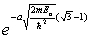
E) None of these is correct.
A)
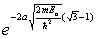
B)
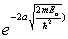
C)
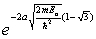
D)
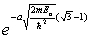
E) None of these is correct.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
48
The wave function for the energy level in a cubical box of side L that corresponds to the quantum numbers 1, 2, and 3 is
A) 1,2,3 = A sin( x/L) sin(2 x/L) sin( x/L)
B) 1,2,3 = A sin( x/L) sin( x/L) sin(3 x/L)
C) 1,2,3 = sin(2 x/L) sin(3 x/L)
D) 1,2,3 = A sin( x/L) sin(2 x/L) sin(3 x/L)
E) 1,2,3 = 2A sin( x/L) sin(2 x/L) sin(3 x/L)
A) 1,2,3 = A sin( x/L) sin(2 x/L) sin( x/L)
B) 1,2,3 = A sin( x/L) sin( x/L) sin(3 x/L)
C) 1,2,3 = sin(2 x/L) sin(3 x/L)
D) 1,2,3 = A sin( x/L) sin(2 x/L) sin(3 x/L)
E) 1,2,3 = 2A sin( x/L) sin(2 x/L) sin(3 x/L)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
49
In three dimensions, the Schrödinger equation for the infinite square-well potential
A) has a solution of the form (x,y,z) = A sin k1x sin k2y sin k3z, where the k's are wave numbers and the constant A is determined by normalization.
B) predicts energy states described by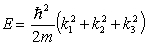 .
.
C) predicts energies and wave functions that are characterized by three quantum numbers.
D) allows multiple quantum states corresponding to the same energy level.
E) All of these are true.
A) has a solution of the form (x,y,z) = A sin k1x sin k2y sin k3z, where the k's are wave numbers and the constant A is determined by normalization.
B) predicts energy states described by
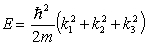 .
.C) predicts energies and wave functions that are characterized by three quantum numbers.
D) allows multiple quantum states corresponding to the same energy level.
E) All of these are true.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
50
A particle is confined in a three-dimensional box with L1 = L, L2 = 2L and L3 = 3L. The energy levels of the particle are given by
A)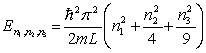 .
.
B)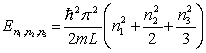 .
.
C)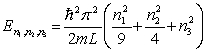 .
.
D)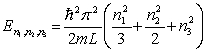 .
.
E) None of these is correct.
A)
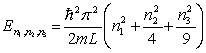 .
.B)
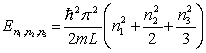 .
.C)
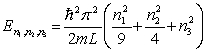 .
.D)
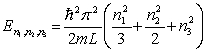 .
.E) None of these is correct.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
51
A particle of mass m is confined in a two-dimensional box that has sides Lx = L and Ly = 2L. By what factor is the energy of the 3rd excited state larger than the energy of the ground state?
A) 5/4
B) 13/5
C) 17/4
D) 17/5
E) 4
A) 5/4
B) 13/5
C) 17/4
D) 17/5
E) 4

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
52
You put 5 non-interacting identical fermions each of mass m into a 1-d box of dimension L. You then put 10 non-interacting bosons each of mass m into a 1-d box of length 2L. Which system has the lowest ground-state energy and what is the value of the fermion system ground-state energy divided by the boson system ground-state energy?
A) fermion system, 19/10
B) boson system, 10/19
C) boson system, 38/5
D) fermion system, 5/19
E) none of the above
A) fermion system, 19/10
B) boson system, 10/19
C) boson system, 38/5
D) fermion system, 5/19
E) none of the above

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
53
Particles that have symmetric wave functions and are not subject to the Pauli exclusion principle are called
A) quarks
B) leptons
C) fermions
D) bosons
E) None of these is correct.
A) quarks
B) leptons
C) fermions
D) bosons
E) None of these is correct.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
54
The number of degenerate states in the third excited state for a particle in a three-dimensional box with L1 = L2 = L3 is
A) 2
B) 3
C) 4
D) 5
E) 6
A) 2
B) 3
C) 4
D) 5
E) 6

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck


